低温加热下小型锂电池模组的电热性能研究
朱 峰,姜景栋,何颖源,陈永翀
(中国科学院电工研究所,北京 100190)
锂离子电池作为一种能量密度高、响应速度快、循环寿命长的电化学储能元件,近年来已经广泛应用于电动汽车、规模储能和移动电子设备等领域。然而,锂离子电池的工作温度一般在0~45 ℃范围内,若电池在0 ℃以下进行充放电,将受到离子电导率和扩散速率下降的制约,导致电池内部的电化学反应速率减缓,并增加负极析锂风险,甚至威胁电池的循环寿命和安全性能。因此,锂离子电池在低温下的快速加热策略已经成为了行业内亟需解决的关键问题之一。
目前,锂电池的低温加热策略可以分为外部热源加热和内部自加热两种方法。其中,外部加热主要利用高温外部热源,通过热传导或热对流的方式加热锂电池,文献[1]中总结外部加热的加热速率范围在0.35~0.86 ℃/min。虽然外部加热法存在能量效率低、加热温度不均等问题,但是由于其装置简单、成本低廉,在电动汽车和储能装置中依然得到了广泛的应用。内部自加热法主要利用电池在充放电过程产生的热量加热电池,由于锂离子低温放电过程不存在析锂风险,因此常采用放电模式对锂电池进行加热。内部自加热法可以分为直流放电法,交流加热法和镍片加热法。对于直流加热法,Wu 等[2]发现18650 锂电池在2C恒流放电模式下,温升速率为4.76 ℃/min。交流加热法是通过高频率、周期性的充放电,充分利用电池自身产生的焦耳热实现加热电池的方法。Jiang 等[3]通过优化交变电流幅值,可以实现加热速率为3.73 ℃/min 的加热效果,同时交流加热法对电池的寿命衰减影响较小。镍片加热法是Wang 等[4]于2016 年提出的新型加热方法,通过在电池内部嵌入镍片,在放电过程中依靠大电流产生的焦耳热加热电池,其加热速率可达60 ℃/min。
虽然现有的电动汽车和储能集装箱等大型储能装置中均已配备了适当的加热装置,但是对于电动自行车或滑板车等小型电池模组,在成本的限制下仍然主要依靠直流放电加热方式,导致电池模组尺度下的电压与温度不一致问题突出[5]。因此,本文基于不同温度下电池放电试验结果,建立电池集总参数电-热耦合模型,分析了不同放电倍率下电池模组中的热电不一致特征,并且探索了锂电池低温脉冲放电预热策略的可行性,对于小型电池模组加热方式的开发具有实际意义。
1 试验方案
1.1 材料与设备
本研究所采用的电池为18650 磷酸铁锂电池,标称容量为1.8 Ah。所用试验仪器包括:CT2001B 蓝电电池测试系统,SMC-80-CB-DC 电池专用高低温试验箱,DT-3891 四通路热电偶测温仪。
1.2 测试步骤
为了测试电池在不同温度下的放电性能,依据GB/T 31486-2015《电动汽车用动力蓄电池电性能要求及试验方法》中的相关要求设计测试步骤。具体如下:(1)在室温25 ℃下,以1.8 A(1C)恒流充电至3.65 V,之后转为恒压充电,当电流降至0.09 A(0.05C)停止充电,充电后搁置1 h;(2)进行低温测试时,先将电池在低温(-20、-10、0 ℃)下搁置24 h,然后以1.8 A 放电至2.5 V,记录放电容量和数据,测试完成后再依据步骤1 进行充电;(3)在进行高温测试时,将电池在(10、20、30、40 ℃)搁置5 h,然后以1.8 A 放电至2.5 V,记录放电容量和数据,测试完成后再依据步骤1 进行充电。
2 集总参数电-热耦合模型
2.1 集总参数模型控制方程
由于18650 电池尺寸效应较小、内部温度较为均匀,因此可以基于集总参数模型去分析电池的热电耦合特征。集总参数模型的建模方法主要依据文献[6],核心思想是将电池的电化学反应抽象成为三个表达式,分别计算电池中线性的欧姆极化VIR,非线性的电化学极化Vact和浓差极化Vcons,进而获得电池的使用电压Ubatt,其表达式如式(1)所示:

式中:Uocv为电池的开路电压;SOCave为电池的平均荷电状态,可由经典的安时积分法计算。
欧姆极化可以看作是电流流经电池中的欧姆电阻产生的,因此会随着电流的变化而线性变化,其表达式如式(2)所示:
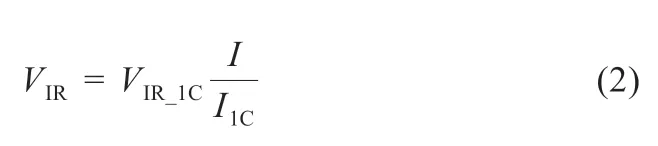
式中:VIR_1C为电池1C放电时的欧姆过电位;I为外加电流;I1C为1C下的放电电流,可以通过I1C=Qbatt/3 600 计算得出。
电化学极化是电极颗粒表面的电化学反应速率与电子迁移速率的不一致导致的,正负极的表达式相同,可以依据Bulter-Volumer 理论得出:
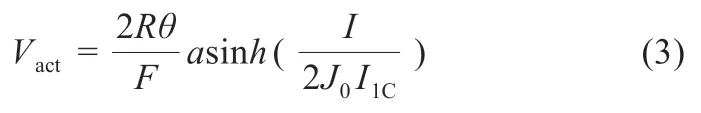
式中:R为摩尔气体常数;θ 为温度;F为法拉第常数;J0为无量纲电荷交换电流。
浓差极化是电极颗粒内外的锂离子浓度差异导致的极化过程,则可以用电极颗粒表面的电压减去颗粒的平均电压计算得出,表达式为:
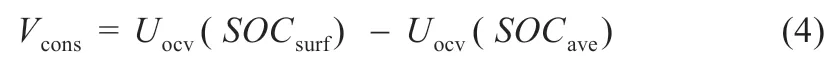
式中:SOCsurf和SOCave分别为电极颗粒表面与平均的电荷状态。
由于式(4)中的两个参数均在式(1)出现,只需计算电极颗粒表面的开路电压Uocv(SOCsurf)即可完成式(1)。为了获得电极表面的SOC,可以依据圆形颗粒的菲克扩散定律计算,表达式为:
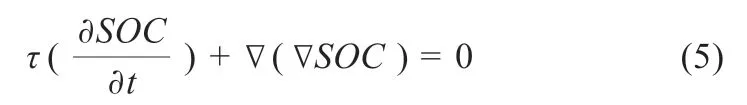
式中:τ为扩散时间常数;t为时间。若将颗粒中心和颗粒表面位置系数分别用X=0 和X=1 代表,那么这两个位置的SOC变化率可由式(6)~(7)得出:

式中:N为颗粒形状系数,对于球形坐标取3。在Comsol 软件中对式(6)~(7)进行表面积分,即可到颗粒表面的SOC值。
2.2 热模型控制方程
建立集总参数电池模型的关键在于确定VIR_1C、J0和τ三项参数,相关研究认为该三项参数均可视作温度的函数[7],因此首先需要利用电池的热模型计算电池的平均温度。锂离子电池在充放电过程中的产热可依据经典的Bernardi 生热理论进行计算,其表达式为:

式中:Uocv、Ubatt与为荷电状态(SOC)的函数。若将生热率q引入电池的能量守恒方程,即可实现电池的热电耦合过程并且获得电池的平均温度,假设电池只通过表面与空气进行对流换热,那么三维锂离子电池能量守恒方程为:

式中:ρe为模型的等效密度;cpe为等效比热容;k为等效导热系数;h为对流换热系数;θ为电池温度;θamb为环境温度。相关等效参数均按照文献[8]中的结果。
2.3 仿真模型参数
本文所研究的对象是由48 个18650 锂电池组成的二维电池模组模型,如图1 所示。为了简化计算,选择模型的左半边作为计算域,并将电池单体由下向上进行编号。电池模组始终处于-10 ℃的环境下,模组壳体与外界换热系数设定为10 W/(m2·℃),电池单体间隔部分为能够自然对流的空气。为了获得VIR_1C、J0和τ 三项参数的表达式,本研究首先建立不同温度下电池单体的集总参数模型,基于最小二乘法逐步迭代仿真结果,使其与试验结果匹配良好。将不用温度下的三项参数值进行拟合,可以得出参数与温度的表达式,结果如表1 所示。此外,电池的开路电压通过试验测得,而则依据文献[9]中的表达式。最后,将上述表达式统一嵌入到电池模组模型中,形成能够体现电池单体热电特征差异的模组仿真模型。

表1 模型参数表达式

图1 电池模组几何结构
3 结果与讨论
3.1 试验与仿真结果对比
图2 为不同温度下电池1C放电的试验与仿真结果,可以看出对于磷酸铁锂电池,其30 和40 ℃的放电曲线比较接近,而随着温度的不断下降,电池的放电容量呈现不断减小的趋势,并且电压平台下降幅度大,极化现象十分明显。比如在0 ℃时,其放电容量只有额定容量的50%;当温度降至-10 ℃时,放电容量仅为0.5 Ah,占额定容量的27%,并且放电平台几乎消失。仿真结果基本保持了与试验结果相同的趋势,二者的差异在5%以内。此外,为了测试电池在不同放电倍率下的热电特征,本文又设计了常温下的1C和2C放电试验,所测温度为电池表面中心处的温度,结果如图3 所示。从图中可以看出,仿真结果能够较好地体现电池的真实放电过程,特别是电池在2C放电初期电压先下降,之后由于温度效应而缓慢上升的现象,仿真结果也呈现相同的规律。在图3(b)所示的温升结果中,试验与仿真结果的最终温度基本相同,但是温升过程中存在1~2 ℃的温差,这是由于模型所采用的热物性参数为文献中的参考值,加之简化了试验过程中的边界条件,导致仿真与试验存在一定误差。总之,本文所建立的单体模型能够较好地反应电池在不同温度及不同倍率下的热电特征,可以作为后续建立电池模组模型的基础。
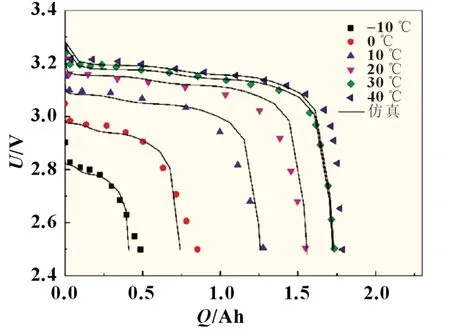
图2 不同温度下电池1 C放电的试验与仿真结果

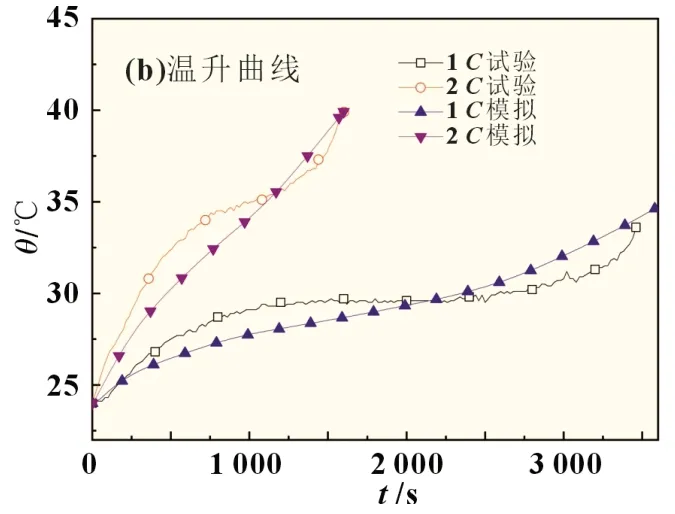
图3 常温下不同倍率放电时的放电曲线与温升曲线
3.2 直流放电加热
为了分析电池模组在低温条件下通过直流放电的加热效果,首先模拟了1C放电下模组内部的热电特征(截止电压为2 V)。图4 为电池模组在1C放电下的温度分布,在放电过程中电池温度逐步升高,在3 000 s 时刻达到25 ℃。然而由于外界环境始终较低,使模组内部的边缘空气区域始终在0 ℃以下,这也导致了模组内部的温度差异随放电的进行而愈加明显。受到模组排列与外界低温两个因素影响,处于模组中心的电池(N15)始终拥有最高温度,而边缘的电池(N1)拥有最低温度,二者的温差在放电3 000 s 时达到5 ℃左右。由此可知,模组内部最大的电压差异也应存在于N1 和N15 之间,结果如图5 所示。在低温放电初期,电池产生了较大的极化,虽然使放电平台产生了大幅度下降,但是也会促进热量的产生,使温度急剧升高,进而使电池的放电平台曲线逐步上升。在这一期间,N1 与N15 两个电池电压差也逐步扩大,特别是在放电结束阶段,N1 电池率先达到放电拐点后电压急剧下降,而N15 电池虽然前期电压平台较高,但是后期的电压下降幅度则更为明显,两个电池在该阶段产生了最高为0.3 V 左右的电压差。因此,通过计算N1 与N15 两个电池的温差与压差,可知在低温直流放电下,在放电后期电池模组内部的热电差异十分显著。

图4 电池模组在1 C放电下的温度分布
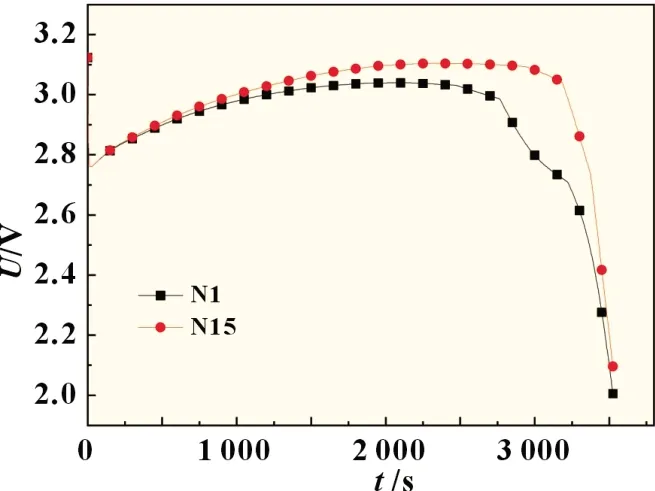
图5 模组在1 C放电下单体N1与单体N15的放电曲线
为了对比不同放电倍率对模组热电差异的影响,选择了0.5C、1C和2C三种工况并计算了模组内部的最大压差与温差变化情况,如图6 所示。对于压差结果,0.5C和1C放电过程都具有压差前期缓慢上升,后期急速上升之后迅速下降的特征,而二者的温差结果也有同样规律。这是由于模组中拥有最低温度的电池单体N1 在放电后期的极化逐步增大,使其温度在最后阶段又产生了一次明显升高,导致温差下降。而对于2C放电过程,虽然其温差随着放电过程逐步增加,并在最终达到8 ℃,但是其压差始终保持在0.05 V 以下,这是由于2C放电末期模组内的温度保持在40 ℃左右,在该范围内的放电曲线比较接近。总之,在低温直流放电过程中,模组内的最大压差与倍率呈负相关,而最大温差与倍率呈正相关,在选择加热倍率时应综合压差、温差、温度与寿命影响等因素进行选择。

图6 不同倍率下电池模组的最大压差和最大温差
3.3 脉冲直流放电预热
与直流放电加热相比,脉冲放电加热因其可以充分利用电池的欧姆产热而降低极化产热,并且对寿命的影响较小,更加适用于电池在低温条件下的加热策略开发。本研究尝试采用先脉冲直流放电预热,再1C持续放电的工作模式,预热时间为180 s,脉冲时间与间隔均为1 s,脉冲放电倍率选定为2C、3C与4C。图7 为不同倍率脉冲预热下单体N1 的温升情况,在前180 s 内,由于高倍率脉冲放电的作用,采用预热的工况温度出现显著的上升,在4C脉冲放电下可以达到10 ℃,其加热速率为6.67 ℃/min,基本能够满足后续的放电起始温度需求。而在后续恒流放电过程中,电池的直流放电也在不断加热电池,最终三种工况的最终温度与无预热的直流放电结果比较接近。图8 为不同倍率脉冲预热下模组内的最大压差与温差结果,可以看出在脉冲预热阶段,模组内压差随倍率的增大而增加,这种特征一直保持到之后的1C放电阶段。值得注意的是,在放电末期压差会出现一个阶跃式的增加,其值接近0.5 V。这是由于在实施预热之后,N15 电池温度有所升高,使其出现电压拐点的时间有所延后,导致放电末期与N1 的压差更加明显。从温差结果对比来看,高倍率的脉冲预热也将导致更大的温差。总之,脉冲直流放电预热可以在短时间内将电池加热至合适的放电温度,但是要适当调整放电截止电压,避免后期压差过大的问题。

图7 不同倍率脉冲预热下单体N1的温升情况

图8 不同倍率脉冲预热下模组内的最大压差与温差
4 结论
本文基于不同温度下电池单体的放电试验,将集总参数模型中的1C欧姆过电位VIR_1C、无量纲交换电流密度J0和扩散因子τ 拟合为温度的函数,从而建立了能够反映小型电池模组热电差异的集总参数电-热耦合模型,且仿真结果与试验结果匹配良好。通过分析低温直流放电加热过程中的温度分布与电压变化,以及不同倍率下热电不一致性,发现模组内的最大压差与倍率呈负相关,而最大温差与倍率呈正相关。此外,低温脉冲放电预热策略可以实现的最大加热速率为6.67 ℃/min,然而在后续恒流放电中不同脉冲倍率预热的电池温度会逐步趋于一致,并且在放电结束阶段产生近0.5 V的压差。因此在设计脉冲预热策略时,应适当提高放电截止电压,保证电池模组的电性能一致性。

