基于VOF相追踪的液滴撞击不同壁面振荡行为研究
尹宗军,苏 蓉,丁 坚,张子豪,李 勇
(安徽信息工程学院 机械工程学院,安徽 芜湖 241100)
1 引言
液滴在固体表面上的润湿应用于许多领域,如超疏水表面、印刷、自清洁表面和集水器[1-3]。对于超疏水表面和自清洁表面来说,使用表面微结构和化学表面处理壁面,可使得液滴撞击后能够发生弹跳,有利于微纳米电子元器件的散热以及防雾防冰;对于印刷来说,油墨喷射纸面时若发生反弹或飞溅将不利于字迹的清晰度;对于集水器来说,在海风多频且缺少淡水的地区,若微小液滴能在壁面凝结形成水珠而后收集则有助于解决淡水资源缺乏问题。可见,理解液滴撞击动力学及其在相关参数范围内液滴的碰撞结果对现有工程应用具有重要研究意义。
近几年,国内许多学者致力于液滴撞击动力学的研究。伊贵娜[4]采用多体耗散粒子动力学方法研究壁面上单液滴和多液滴的撞击及聚并行为。周鑫等[5]考虑液滴物性参数随温度的变化,模拟了液滴撞击流动行为,研究表明固液传热作用会影响液滴铺展直径,但不改变运动趋势。彭启[6]主要研究了层级微槽超疏水表面液滴合并弹跳行为,以及微槽疏水与层级微槽超疏水表面蒸汽冷凝换热特性。王欣[7]通过改变撞击We数、亲水表面的亲水性、疏水条纹的疏水性和疏水条纹的宽度,研究了液滴撞击亲水性表面上疏水条纹的分裂特性。于凡斐[8]提出了一种双组分液滴撞击超双疏非润湿表面的新型动态行为,该表面能够促进撞击诱发飞溅的提前发生。彭启等[9]制备了CuO纳米结构和矩形微槽相结合的层级微槽超疏水表面,研究了三种表面张力的单个液滴在微槽内的受限生长特征以及槽内变形液滴与槽外正常液滴的合并弹跳行为。韩立宝[10]开展了环槽超疏水表面的液滴碰撞实验,探究了环槽结构对于液滴横向运输的影响规律。王昊[11]开展了液滴撞击不同倾角的超疏水沟槽表面的铺展和接触时间动力学特性的研究,并根据沟槽方向与斜面方向所成角度将实验分为横向撞击和纵向撞击。杨延杰[12]研究了液滴撞击亲疏水表面的铺展和迁移规律,主要工作包括液滴撞击光滑表面的模态判断,液滴撞击润湿性梯度表面的动态过程,液滴撞击楔形亲疏水表面铺展研究。韩丁丁[13]揭示了粘弹性抑制液滴在疏水壁面上反弹的机理,实现了高分子溶液撞击超疏水壁面的不同模态。姚一娜等[14]研究了液滴的碰撞角度和We数对碰撞过程中液滴前后沿点位移、最大铺展直径、滑移距离等的影响。张春雨[15]研究了剪切流中复合液滴运动和平板上复合液滴构型之间的转化。闫哲[16]探究了不同的表面润湿性、撞击速度及表面微尺度结构对液滴动态特性的影响。高明谦[17]认为超疏水表面具有较大接触角和较小滚动角,液滴撞击其上会产生弹跳现象,并通过改变柱状阵列的倾角间接改变最小柱间距值从而实现对液滴的弹跳状态、弹跳方向及弹跳时间的控制。张博[18]考察了液滴润湿行为与表面纳微结构关系。李大树[19]对传热、液固润湿、Marangoni应力和接触角滞后现象进行了数值求解。梁超等[20]模拟了液滴以相同速度撞击到接触角分别为63°、90°、118°和160°的固体壁面,结果表明固壁的亲憎水性对液滴撞击表面后的形态演化有较大影响。
考虑液滴与壁面的相互作用对液滴撞击后的形态演化以及液滴因粘性耗散而产生的振荡行为具有重要的影响,结合液滴对撞击不同润湿壁面的普遍性,本文将以毫米尺寸水滴撞击不同固体壁面作为研究载体,着重分析液滴在撞击不同润湿表面的振荡行为和振荡特性,为理解壁面作用对液滴振荡行为的影响提供模拟应用依据。
2 控制方程与参数设置
2.1 基于VOF相界面追踪的流体控制方程
在本研究中,液滴因撞击而在内部产生激波的传播时间尺度很短(约D0/V0×10-4),因此可以忽略液滴撞击固体表面引起的液体可压缩性的影响。此外,气体的可压缩效应也被忽略,因为气相的马赫数Ma=V0/c0为O(10-3)(c0表示空气中的声速)。因此,假设液体和气体这两种流体都是不可压缩的牛顿流体,并指定为层流流体,且考虑这两种流体之间的表面张力γLV和重力。此外,使用ρV和μV分别表示空气的密度和粘度,ρL和μL用于表示液滴的物理特性。
在VOF计算中,可以将固体表面上铺展的不互溶液气两相流假设为一种有效流体。由于每个单相流的物理性质(例如密度和粘度)被认为是恒定的,因此体积分数变量c可以用来跟踪该有效流体的相分数(相分数c=0表示气相,c=1表示液相,c介于0和1之间时代表两相界面区域)、密度ρ和粘度μ。更具体地说,密度ρ可以用体积分数变量c表示为ρ=cρL+(1-c)ρV,粘度定义为ρ=cμL+(1-c)μV。就此而言,该有效流体流动的控制方程包括连续性方程,带表面张力项的Navier-Stokes方程和相分数的扩散方程[21],如下所示:
(1)
(2)
(3)
式中,u≡(u,v)表示为速度矢量,p表示压强,D定义为Dij≡(∂iuj+∂jui)/2,g重力加速度,δ为迪拉克算子,κ表示界面的平均曲率,n表示从液相流出的界面的单位法线。
上述控制方程的离散格式可参考文献[22],如下所示:
(4)
(5)
(6)
其中,下标n和n+1/2分别表示相应的时间节点,u*表示辅助速度场。所有VOF数值模拟均使用GERRIS程序(一个用于求解描述流体流动的偏微分方程的开源软件程序)进行。
2.2 建模与参数设置
液滴撞击壁面模型可简化为二维模型LX×LY=2L×L,其中L等于8 mm,如图1(a)所示。初始,压强p设置为0,气体内部u和v(x、y方向上的速度分量)设置为0。模拟区域的大小选择应保证直径为D0的液滴能够自由扩散。对于底部壁面,采用滑移边界条件(u=u0+λ∂u/∂y)来描述固体表面与液滴之间的相互作用,λ为滑移长度,u0为壁面的移动速度。液滴与固体表面之间的初始距离h选择为h=D0。如果h的参数值太大,撞击速度V0的控制精度较低,计算量会增加。相反,气相流动的影响可能会被忽略,固体-液滴界面的计算误差较大,这意味着初始距离h不应太小。

(a)计算模型 (b)局部自适应笛卡尔网格
为了在不增加大量计算量的情况下保证液气界面的计算精度,对液滴周围区域进行动态自适应局部笛卡尔网格细化。如图1(a)所示,由高分辨率网格包围的红色区域表示液滴,其中VOF体积变量c的值为1。网格细化的最大和最小级别分别为10和6,相应的计算单元尺寸分别为L/210和L/26(即7.8125×10-3mm和1.25×10-1mm)。根据液滴运动和形状变形,网格分辨率沿液滴-气体界面变化,局部网格中自适应细化的判据可以表示为:
‖c‖Δx/max‖u‖>δ
(7)
式中,‖c‖是VOF体积分数变量c的值,Δx为子网格的尺寸,max‖u‖为流体穿过局部单元的最高速度,δ为阈值参量。只有当每个时间步的‖c‖Δx/max|u|小于δ/4时,GERRIS软件中网格才会粗化。液滴-气体界面的急剧变化对应于高网格分辨率,因此阈值δ指定为0.01。如图1(b)展示了液滴动力学包括撞击、铺展、回缩和反弹行为所对应的局部笛卡尔网格。
2.3 验证
为了进一步验证VOF模拟算法的准确性,将水滴(D0=2.0mm,V0=0.31m/s)与固体超疏水表面(静态接触角θE=157°)的VOF模拟与文献[23]中的实验进行比较,如图2(a)-(b)所示。在计算中,水和空气的密度和粘度分别设定为ρL=9.98×102kg·m-3/ρV=1.2kg·m-3,L=1.003×10-3N·s·m-3/μv=1.8×10-5N·s·m-3,表面张力设置为γLV=7.5×10-2N·m-1。经历扩展和后退过程后,液滴在特征时间t=11.2ms时完全脱离固体表面。如图2(c)所示,最大润湿直径及其相应时间分别约为1.85mm和3.6ms,模拟结果与实验结果一致。该数值策略可以准确地预测液滴的变形,并很好地解决了网格无关性问题。
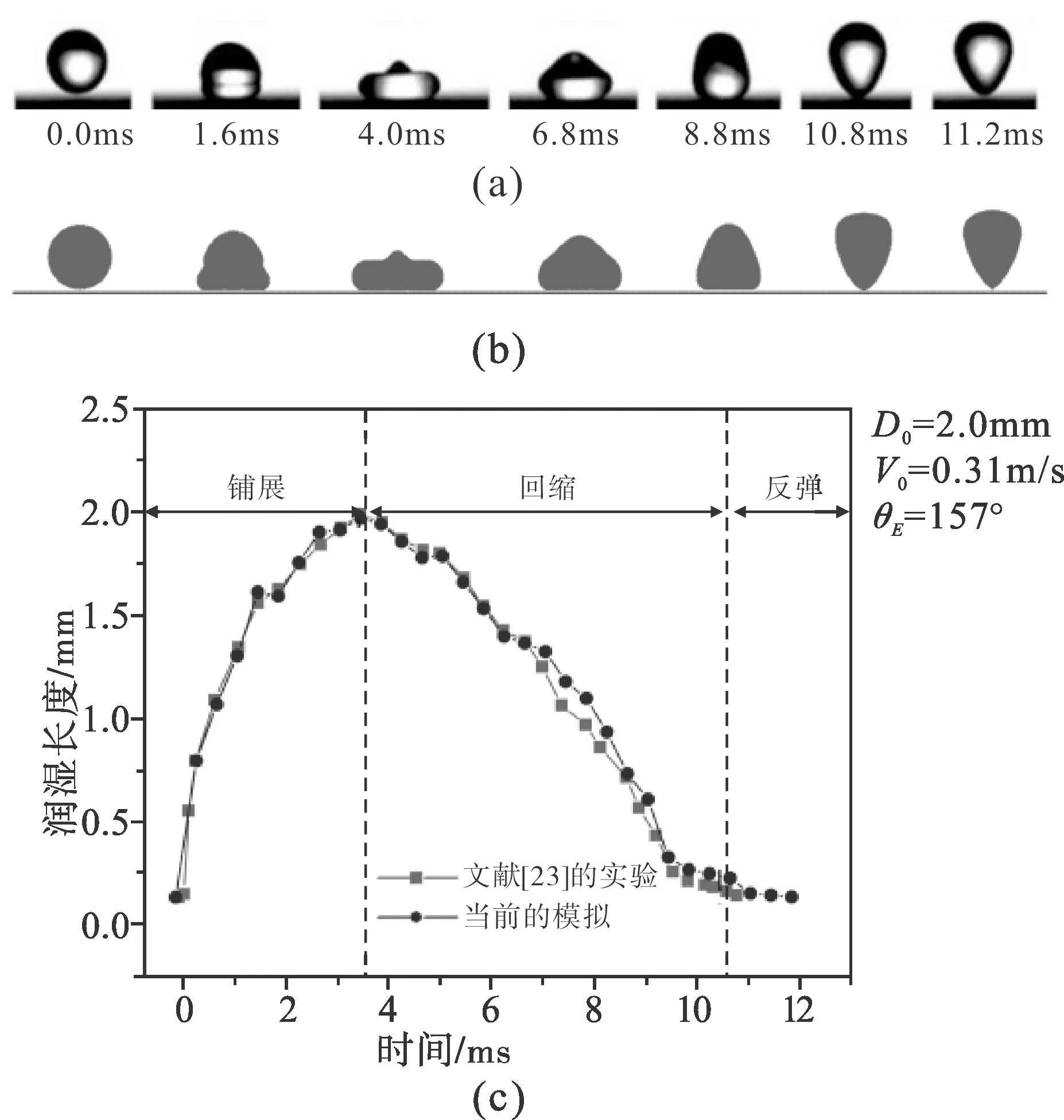
(a)液滴反弹的实验[23];(b)液滴反弹的VOF模拟 (c)当前模拟与文献[23]实验对比
3 液滴撞击壁面的振荡行为仿真模拟
3.1 不同速度下液滴撞击壁面的运动演化
液滴撞击固体表面后,会导致弹跳、飞溅或粘附,这在很大程度上取决于撞击速度[24]。这个撞击速度不能太大,否则液滴可能会在固体表面上反弹或发生飞溅。因此,液滴的撞击速度V0设定为0.1m/s、0.2m/s、0.3m/s、0.4m/s和0.5m/s,以便研究液滴撞击壁面后的振荡行为。此外,水滴的直径指定为D0=1.6mm,壁面静态接触角为θE=90°。
图3显示了不同撞击速度下液滴撞击光滑固体表面的运动演化图以及部分速度矢量场。图4显示了铺展因子β的时间变化曲线(定义为β=L/D0,L为当前润湿长度)。时间节点t=0.0定义为水滴刚接触到固体表面时刻,此时β=0。对于较低的速度V0=0.1m/s(见图3(a)),可以看到液滴经历了铺展和回缩阶段。碰撞开始时,由于固体表面的阻挡,液滴的法向动量发生变化。随着高度的降低,液滴的下部形成向外的径向流动(见t=2.0ms)。直到t=6.2ms,该径向流动达到最大润湿面积,此时液滴运动的驱动力变为毛细力。相应地,扩展因子β增加到最大,即βmax=2.43,如图4(a)所示。之后,液滴向内收缩,从中心升起。液滴的内聚力迫使湿滴面积减小,β值开始减小。在表面张力和惯性力的综合影响下,液滴达到一定高度而不反弹。在t=13.8ms时,β减小到最小值0.74。在随后的运动中,重力产生向下的运动趋势,使水滴落下。当t=19.8ms时,液滴再一次达到当前最大润湿面积。随后,因粘性耗散不断铺展/回缩,直到水滴处于平衡状态,平衡时间甚至超过400.0ms。在V0=0.2m/s、0.3m/s和0.4m/s的情况(见图3(b)-(d)),上述三种情况下的βmax值约为2.58/6.4ms,2.77/6.6ms和3.14/7.6ms(如图4(a)所示)。对于V0=0.5m/s(见图3(e)),液滴中心出现一个孔,这是由于弯曲界面的夹断。在时间t=8.2ms时,它的最大铺展因子βmax等于3.48。
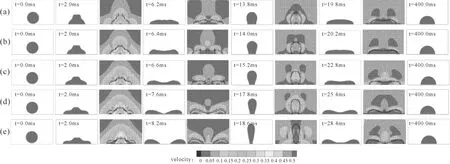
(a)0.1m/s (b)0.2m/s (c)0.3m/s (d)0.5m/s (e)0.5m/s
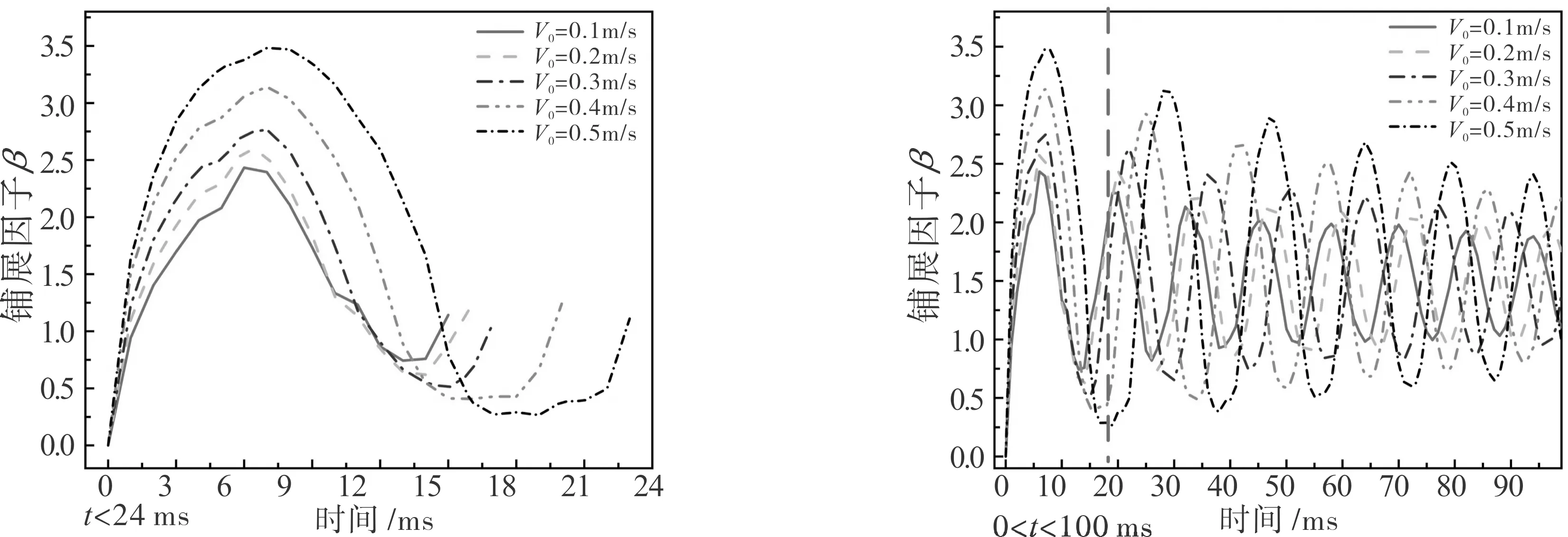
(a)第一个振荡周期 (b)100ms内的振荡曲线
为了定量描述振荡液滴变形特征,如图4(b)所示为100.0ms内铺展因子β的时间变化曲线图。铺展因子因子β在100ms内的变化足以让我们确定振荡特性的关键特征(即平均振幅比χ和平均振荡周期τ)。很明显,液滴振荡的振幅随着V0的增大而增大。V0的大小在0.1m/s到0.5m/s之间变化时,χ值为依次为1.045、1.052、1.058、1.064和1.076,τ的对应值分别为13.32ms、13.62ms、14.64ms、15.66ms和17.12ms,因此,平均振幅比χ和平均振荡周期τ均随撞击速度的增大而增大。可见,撞击速度的增加并不利于削弱液滴振荡。
3.2 液滴撞击不同润湿壁面的振荡特性
除撞击速度外,壁面润湿性在液滴碰撞动力学行为中也起着重要作用。液体/气体界面的接触角通常被用来描述液滴润湿固体表面的能力。若液滴静止在理想的固体表面上,这个接触角称为静态接触角θE。对于较低的θE(例如θE<90°),此时壁面附着力较强,液滴倾向于粘附在壁面上。如果θE较高(如θE>150°),由于壁面阻力较小,液滴撞击后容易破碎或反弹。因此,接触角小于90°的表面为称为亲水表面,而大于90°的则为疏水表面。然而,界面动力学揭示了液滴存在接触角迟滞效应,接触角在液滴铺展/回缩过程中是动态变化的。这种接触角被称为动态接触角θD,其与接触线的速度有关。但本文假设液滴在光滑表面上移动的接触角等于静态接触角θE,通过数值模拟壁面的静态接触角范围为θE=70°至110°(包括从部分湿润到非湿润)对液滴振荡行为的影响。这里主要研究D0=1.6mm的液滴低速(V0=0.2m/s)撞击不同润湿表面的振荡特性。
图5显示了不同时间下的液滴撞击在不同润湿表面上的运动演化图。在液滴铺展过程中,部分速度矢量场也在图中显示。所有这些图像都呈现出液滴铺展/回缩的行为。很明显,随着θE值增大,最大润湿长度减小。对于较小的θE值(见图5(a)-(c),即θE=70°、80°和90°),可以观察到液滴中心弯曲界面的形成。当θE=110°时,液滴中心不形成弯曲界面,原因是壁面与液滴间粘附力小于液滴自身的内聚力,如图5(d)中所示。对于液滴形状处于平衡状态时,θE值较小的情况(例如θE=70°)具有较大的静态润湿面积。

(a)70° (b)80° (c)90° (d)100° (e)110°
图6(a)给出了铺展因子β的第一个振荡周期。对于考虑的所有液滴碰撞,β值起始都会增加,然后随着时间的推移而减少。βmax值在θE的第一个循环期间得到,可以看出当接触角从70°变化至110°时,βmax值及其对应的时间节点分别为3.66/9.2ms、3.06/7.8ms、2.55/6.8ms、2.21/6.5ms和1.87/6.1ms。因此,对于较小θE值(例如θE=70°),βmax值较大,对应达到βmax时的时间节点也较长。这是因为较小θE值对应于较强的壁面粘附,这会促进液滴润湿并导致βmax增大。图6(b)显示了相应的铺展因子β在100ms内的时间变化曲线。可以清楚地观察到几个液滴铺展/回缩的振荡周期,平均振幅比χ和平均振荡周期τ分别为1.051/17.1ms、1.050/15.2ms、1.049/13.7ms、1.041/12.7ms和1.028/12.6ms。表明随着θE值的增加,χ和τ的值均减少。θE的减小可以有助于抑制液滴的振荡幅度,并延迟平均振荡周期,但润湿面积较大。
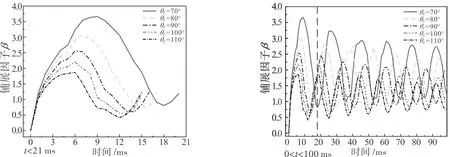
(a)第一个振荡周期 (b)100ms内的振荡曲线
4 结论
固体表面润湿性对液滴在壁面上的振荡行为重要影响,通过引入描述壁面润湿特性的壁面接触角,利用VOF相界面追踪法对液滴撞击不同壁面的振荡特性进行了仿真模拟,分析了液滴速度和壁面润湿性因素对液滴振荡特性的影响。仿真结果表明壁面接触角减小有助于抑制液滴的振荡幅度,并增大平均振荡周期,但润湿面积较大。在海风多频而缺少淡水地区,使用较小壁面接触角的表面收集液滴时,在液滴动态振动过程中液滴与表面接触面积较大、振幅衰减较快有利于液滴附着表面,可有效避免液滴在海风影响下反弹出表面。

