一种改进的D数聚集方法及其在决策中的应用
莫泓铭,徐建林,肖万武
(1.四川民族学院 图书馆,四川 康定 626001;2.四川民族学院 马克思主义学院,四川 康定 626001;3.四川民族学院 体育学院,四川 康定 626001)
决策是一种常见的日常活动,是决策者为实现特定的目标,根据主观、客观的可能性,在既有信息和经验的基础上,借用相关决策方法或工具,对影响决策目标的诸多因素进行分析、判断、整理的过程。一般决策目标所涉及到的因素即决策目标的属性比较多,因此决策通常指多属性决策(Multiple attributes decision making,MADM)[1]。近年来,诸如层次分析法(AHP)[2]、逼近理想解排序法(TOPSIS)等方法用于解决MADM问题,其中各属性的相关参数或指标的评估信息都是必不可少的。然而在现实生活中,获取参数或指标的精确评估信息比较困难。一方面,对指标的量化可能涉及到定性信息、定量信息,甚至有的由于不方便量化而导致信息缺失,即出现不完全信息等;另一方面,决策者在决策评估时,由于自身的专业知识、兴趣偏好等主客观原因,做出的相关评价信息具有不确定性。近年来,学者们提出了模糊数学[3]、粗糙集[4]、证据理论[5,6]等方法用于解决信息不确定性问题,并取得了一定成效。
值得一提的是,证据理论作为贝叶斯概率论的推广,最大优势在于不需要任何先验概率信息,并且将单子集推广到幂集,表达和应用范围更广。然而在运用时,仍面临诸多条件约束与先天不足。为解决这些问题,邓勇教授[7]于2012年提出D数理论,作为证据理论的有效扩展,克服了相关限制与先天不足,信息的表达与处理更加灵活。但在处理不完备信息时容易出现与直觉相悖的结果。基于此,本文提出一种新的D数聚集方法,将缺失的信息有效利用起来,使融合结果更加合理。
1 预备知识
1.1 证据理论
证据理论(Evidence theory)是Dempster[5]于1967年提出,随后由其学生Shafer于1976年进一步推广、完善的一种处理不确定信息的数学工具[6]。不仅能表达不确定信息,还能表达完全不知道的信息。由于具有强大的信息处理能力,证据理论已被广泛应用于故障诊断[8]、供应商选择[9]、多源目标融合[10]等领域,并取得较好的效果。
假设H={H1,H2,H3…,Hn}是一个非空、完全、互斥的集合,辨识框架(Framework of discernment)Ω={H1,H2,…Hn,{H1,H2},{H1,H3}…Ω}由该集合的所有子集及其幂集组成,在该框架上的基本概率指派(Basic probability assignment,BPA)满足:
其中,Ø是空集,A是集合Ω的任意子集。
Dempster组合规则是证据理论的核心,又称为两个BPA的正交和,即将两个不同来源的证据进行融合,得到一个新的证据。Dempster组合规则定义如下:
其中,k是冲突系数,反映两个BPA的相容程度。当k=1时,说明这两个BPA完全一样;k=0,则完全冲突、互斥的,即彼此互相矛盾,此时Dempster组合规则无效,证据理论不适用于此情形。Dempster组合规则满足交换律和结合律,即m1⊕m2=m2⊕m1,(m1⊕m2)⊕m3=m1(⊕m2⊕m3)。当存在多个BPA时,不考虑先后顺序采取一对一进行融合。
1.2 D数理论
证据理论相对传统的贝叶斯概论而言,从单子集到幂集,在先验信息的需要与否,信息的表达与融合等方面都取得了一定成效,应用范围更加广泛。但在运用时,需满足诸多条件:一是集合中的元素必须两两互斥,不能有任何交集。但实际生活中诸如“很好”“好”“一般”等语言评价集,元素之间可能没有明确的界限,甚至相邻的两元素间很可能有一定交集。二是同一BPA概率分配之和必须为1,即完整性约束。但由于设备的软、硬件原因,收集不到足够的完整的信息,或者评估者由于知识水平不足,对评估对象缺乏足够把握等主客观原因,评估时很容易只给出部分信息,即只能给出部分BPA信息,导致BPA信息信任度之和不为1,这在现实生活中是允许的,也是客观存在的,但在证据理论中是不允许的。三是Dempster组合规则的运算时间复杂度高,当证据源的数量呈线性增长时,计算时间复杂度呈指数级增长,不适用于对时间性要求比较高的信息融合决策场景。四是Dempster组合规则在运用时,要求各证据源间必须彼此完全独立,毫无关联,这在实际中很难完全达到。比如在评估时专家有可能受到其他专家的干扰或影响,或者查阅资料时受到历史评估信息的影响等。五是Dempster组合规则的先天“一票否决”制,即著名的“Zadeh悖论”[11]。当某个元素一旦被否决,即信任度被赋值0,不论后面的证据源多么强有力的支持,甚至100%信任,最终的融合结果也为0。
在D数理论中,元素间不强行要求必须互斥,允许评估者根据实际情况给出评估信息,不强性要求评估信息的信任度之和必须完整,即允许信息缺失,解决了证据理论的指数级计算时间复杂度问题等。由于上述诸多优势,D数理论目前已被广泛应用到医疗废物处理技术评估[12]、选址[13]、质量目标评估[14]、紧急决策[15]、交通可持续评估[16]、项目复杂性评价[17]、环境影响评估[18]、风险评估[19]等领域,并与TOPSIS[20]、SWOT[21]、模糊层次分析法[1]等技术联合运用,取得了不错的效果。相关定义如下:
定义1假设Ω是一个有限非空集合,D数是一个映射,即D:Ω→[0,1],满足以下条件:
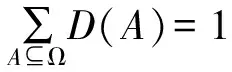
定义2假设Ω={d1,…di,…dn},一种特殊形式的D数D(d1)=ν1,……D(di)=νi,…D(dn)=νn,可简化表示为
D={(d1,ν1)…(di,νi)…(dn,νn)}
属性1 交换不变性。假设在同一个框架上有两个D数,D1={(d1,ν1)…(di,νi)…(dn,νn)}和D2={(dn,νn)…(di,νi)…(d1,ν1)}。若D1和D2的元素di及其对应值νi相同,说明D1和D2完全一样。
例1假设在同一框架上有两个D数,分别为D1={(G,0.3),(F,0.5),(T,0.2)}和D2={(F,0.5),(G,0.3),(T,0.2)},则D1⟺D2,⟺表示二者一样,只是在不同的D数中,顺序不一样。若D1和D2的信任度值之和都为1,说明这两个D数是完备的。
例2假设在同一框架上有两个D数,分别为D1={(A,0.35)},(B,0.55)}和D2={(B,0.55)},(A,0.35)},则D1⟺D2。但D1和D2的信任度值的和都小于1,说明这两个D数是非完备的,这在证据理论中是不允许的,但D数理论是可以的。
属性2 聚集性。假设存在一个特殊的离散型D数,D={(di,νi)},(i=1,2,3…),那么其聚集方法可表示为
(1)
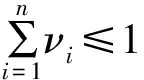
需要说明的是,D数的聚集方法仅适用于特殊的离散型D数,在信息融合上充分利用可大大简化并加快融合过程。
2 改进的D数聚集方法
2.1 D数原始聚集方法的局限
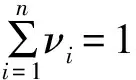
例3假设有10名专家受邀对拟采购的设备A和B基于评估集Ω={1,2,3,4,5,6,7}进行评估,7表示相当好,1表示相当差。由于大家对设备A比较熟悉,所以对其评估等级均为“5”,设备A的评估结果可D数表示为DA={(5,1.0)。当对设备B评估时,有7位专家比较熟悉,其中2位的评估等级为6,其余为7;剩余3位专家不够了解,没有给出评价,则设备B的评估结果表示为DB={(6,0.2),(7,0.5)}。根据D数原始聚集方法,两种设备的最终评估得分分别为:
I(DA)=5×1.0=5
(2)
I(DB)=6×0.2+7×0.5=4.7
(3)
5>4.7,即设备A更优于设备B,但熟悉B的专家认为B更优。一方面从评估等级来看,6>5和7>5;另一方面,虽然给出高评估等级的专家为7人,占总人数的70%,但有3人即30%的专家没有给出信息,D数原始聚集方法将该部分信息直接视为0,导致与直觉不太一致。由此可知,D数原始聚集方法有一定局限,特别是在处理不完备的信息时。
2.2 基于数值比例的D数聚集方法
D数原始聚集方法造成与直觉相悖结果的主要原因在于抛弃了非完备信息的非完备部分的信息,而这部分信息也是有效信息,不能舍去。为解决这一不足,Wang等[22]提出一种基于D数数值比例的聚集方法(简称比例法),如式(4)所示。基于现有评估信息,将缺失的信息按比例分配给现有的评估信息,出发点在于对于认知不完全的专家,可以参考已经给出评估结果的专家的意见进行分配。
(4)
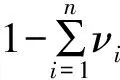
比例法从一定程度上修正了D数原始聚集方法,并取得了良好效果。如表1所示,将非完备部分的信息再分配给现有的评估等级,从而得到充分利用。然而,比例法仅适用于非完备信息下的非单子集信息,而对于单子集信息则无效。对于非单子集的信息,按照比例法的原理,无论现有的评估信息量多么渺小,哪怕无穷小,非完备部分的信息都将毫无保留地分配给现有信息,又将导致直觉相悖的结果出现。

表1 三种D数聚集方法对比
2.3 基于评估等级的D数聚集方法
鉴于基于比例的D数聚集方法在处理单子集方面的不足,本文提出一种基于评估等级的D数聚集方法(简称等级法),将非完备信息的非完备部分信息平均分配所有的评估等级。将属性2修正为:
定义3对于一个离散型D数,简化表示为D={(di,νi)},(i=1,2,3…),聚集方法表示为
(5)
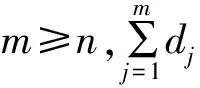
由表1可知,等级法不管是对单子集还是非单子集的处理,无论信息完备与否,聚集结果都更为合理,与直觉也相符,同时也向下兼容D数原始聚集方法。
在评估过程中,如果相关指标及权重信息,则首先需要建立层次化的结构模型,对每个层次每个指标的权重信息纳入评估范围,基于评估等级的加权D数聚集方法,可表示为
定义4假设每个指标的权重与专家的评估结果分别表示为ωk和Di={(di,νi)},(i,j,k=1,2,3,……),则基于评估等级的加权D数聚集方法,可逐步加权求和,表示为:
(6)
其中,Di={(di,νi)}是离散型的,di∈R,m是dj的个数,即评估等级的个数,m≥n;E(D)表示专家在评估时,充分考虑各指标属性的权重与属性值的评估结果。
3 数值验证与结果分析
3.1 数值验证
某公司拟引进摩托车发动机技术,通过对市场上常见摩托车发动机进行摸底,最终确定4种品牌纳入候选评估。为方便专家充分表达评估意见,采用语言评估等级L={很差(I),差(P),一般(A),好(G),很好(E)}供评估使用,邀请10位专家参与评估[22]。在评估时,假如有6位专家认为某个品牌的某项指标很差,其他4位认为差,那么关于该品牌此项指标的评估结果可以用D数表示为:{(I,0.6),(P,0.4)}。假如有3位专家给出的评价是好,6位给出非常好,另一位没有给出评价,则该评估结果用D数表示为{(G,0.3),(E,0.6)},该评估信息是非完备的。需要说明的是,各评估指标信息在本算例中默认相同,忽略权重信息。专家的原始评估信息(数据来源于文献[22])如表2所示。

表2 摩托车发动机评估结果(语言)
为应用D数的聚集方法,需将语言评价集转化为数值评价集,采用文献[22]定义的效用函数如表3所示。表2可转化为表4。

表3 语言集效用函数

表4 摩托车发动机评估结果(数值)
评估信息中存在着非完备信息,如表4所示。采用等级法分步骤地对各品牌摩托车的引擎指标进行融合。以摩托车发动机K为例,由于评估信息是非完备的,融合结果为
(7)
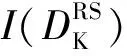
(8)
同理,其他摩托车发动机的评估结果为:
I(DY)=2.10,I(DH)=3.83,I(DB)=2.90
(9)
其中,I(DK)表示K的最后得分,I(DY)表示Y的最后得分,I(DH)表示H的最后得分,I(DB)表示B的最后得分。由式(8)(9)可知,最后排序为H>K>B>Y,故应推荐摩托车发动机H。
3.2 结果分析
为验证本文提出的等级法的有效性,将D数原始聚集方法和比例法再次运用到上述案例,所得到的结果如表5所示。可以看出,三种方法所得到的排序结果是一样的,说明本文提出的等级法是有效的。
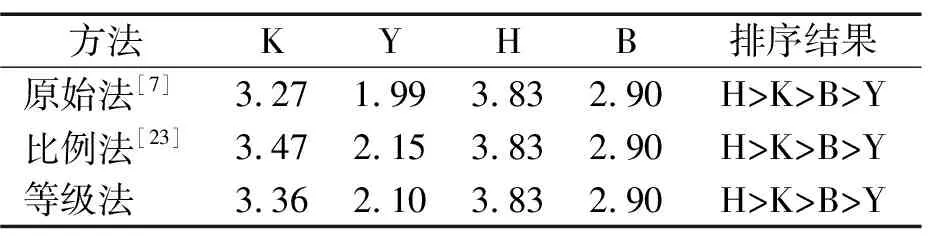
表5 不同的聚集方法结果对比
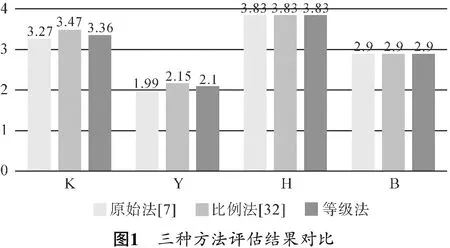
对于完备数据的处理,如图1的H和B可知,三种方法得到的评估数据一样。对于非完备数据的处理,如图1中K和Y可知,三种方法得到的结果大小排序为:比例法>等级法>原始法。造成这种差距的原因主要在于,原始法直接将非完备信息中的非完备部分信息抛弃,因而所得评估结果值最小;比例法则将非完备信息中的非完备部分信息按现有评价信息进行二次叠加分配,忽略了潜在的其它信息,造成“强者愈强,弱者愈弱”的情况,即没有全面对待非完备部分的信息,只是基于现有信息进行分配。而等级法将非完备信息中的非完备部分信息按比例分配给评估等级中的所有信息,一方面考虑了现有的评估信息,另一方面也考虑了未知的潜在信息,因而评估的结果更为全面。
4 结语
本文在对D数原始聚集方法及基于比例的D数聚集方法在处理非完备信息的不足进行充分分析的基础上,提出了一种基于评估等级的D数聚集方法。将非完备信息中的非完备部分信息进行充分利用,平均分配给评估等级,兼顾已有信息与非完备信息。如果信息是完备的,将退化为D数原始聚集方法,说明新提出的方法具有兼容性;如果信息是非完备的,将充分利用非完备部分的信息,说明新提出的方法具有兼容性。实例验证表明,本文提出的基于评估等级的D数聚集方法在信息处理,特别是在处理非完备信息及单子集评估信息等方面具有合理性、全面性、有效性。

