应用张量分析推导柱坐标系和球坐标系中弹性力学几何方程和平衡微分方程

周正峰

(1. 西南交通大学 土木工程学院，四川 成都 610031;2. 西南交通大学 道路工程四川省重点实验室，四川 成都 610031)

物理量及其遵循的物理规律是客观存在的，与选取的坐标系无关[1]. 但是物理量的分量与参考坐标系密切相关，会随着参考坐标系的不同而变化. 为了研究同一物理量及其规律在不同参考坐标系中表达形式的差异和联系，张量分析是十分有力的工具，它不仅能使繁琐的数学推导以及表达式变得简明清晰、便于记忆，而且使分析问题不受具体坐标系的限制，对于一些需要选用曲线坐标系进行分析的问题特别有利. 张量分析能充分展现数学应用于力学分析时的严谨和美感，被近代力学相关教科书和学术论文普遍采用，也是深入学习连续介质力学的必要基础[2].

弹性力学中几何方程和平衡微分方程是应变和应力分析的重要内容，在大多数面向工科学生的弹性力学教材中，直角坐标系和极坐标系中的几何方程都是由线元的应变与位移的关系导出的，平衡微分方程都是由微元体的静力平衡条件导出的[3]. 在直角坐标系中，由于坐标线的方向保持不变，几何方程和平衡微分方程的推导还比较容易，但在平面极坐标系中，由于环向的坐标线是曲线，几何方程和平衡微分方程的推导需要借助作图进行细微分析，推导过程难以掌握[5]. 对于三维柱坐标系和球坐标系，若仍采用作图分析法推导几何方程和平衡微分方程，将会变得非常复杂和困难.

本文应用张量分析详细推导柱坐标系和球坐标系中弹性力学几何方程和平衡微分方程. 首先利用正交曲线坐标系与笛卡儿坐标系单位矢量之间的关系，以及笛卡儿坐标单位矢量为常矢量的特性，从单位矢量变换的角度，推导柱坐标系和球坐标系中的梯度算子，以及单位矢量对坐标的偏导数. 然后根据张量的场论基础，通过微分运算，推导出位移矢量的梯度和应力张量的散度，再根据几何方程和平衡微分方程的张量表达形式，推导柱坐标系和球坐标系中的应变几何方程和应力平衡微分方程. 本文推导过程尽可能详细，使读者在具有最基本的张量知识前提下，能够理解和掌握整个推导过程.

1 正交曲线坐标系下的梯度算子▽

采用张量形式给出的弹性力学几何方程和平衡微分方程，并不依赖所选取的坐标系，在曲线坐标系下仍然成立.

由张量表示的几何方程为[6]

(1)

式中，ε是应变张量；u是位移矢量，▽是梯度算子，▽u表示位移矢量u的梯度，(▽u)T表示位移矢量u的梯度的转置矩阵.要得到正交曲线坐标系下几何方程的具体形式，关键是要求位移矢量u的梯度.

由张量表示的平衡微分方程为[6]

·σ+F=0

(2)

式中，σ是应力张量；F是体力矢量.要得到正交曲线坐标系下平衡微分方程的具体形式，关键是要求梯度算子▽与应力张量σ的内积，即散度.

1.1 正交曲线坐标系下的梯度算子▽

设笛卡儿坐标系为xi，正交曲线坐标系为αi，两组坐标系之间存在对应关系：

xi=xi(α1,α2,α3)

(3)

笛卡儿坐标系中任意一点矢径r对坐标的偏导数是三个相互正交的单位矢量ei，矢径r可表示为

r=x1(α1,α2,α3)e1+x2(α1,α2,α3)e2+

x3(α1,α2,α3)e3

式中，e1、e2、e3分别是笛卡儿坐标系沿坐标轴x1、x2、x3方向的单位矢量，是方向和大小均不变的常矢量，矢径r对单位矢量ei进行分解所得的分量即为坐标xi.与笛卡儿坐标系不同，曲线坐标系的单位矢量沿坐标线αi的切线方向，是随点变化的，等于矢径对曲线坐标αi的偏导数除以拉梅系数hi.根据式(3)，拉梅系数hi为

(5)

则曲线坐标系的单位矢量为

(6)

式中等号右边项的下指标i不是哑标，即对i不求和.将式(4)代入式(6)，可得曲线坐标系与笛卡儿坐标系单位矢量之间的关系为

(7)

在笛卡儿坐标系中，梯度算子为

(8)

假设同一函数，在曲线坐标系中的梯度算子可表示为

(9)

则对于正交曲线坐标系，式中系数为

(10)

将式(7)、式(8)代入式(10)得

(11)

将式(11)代入式(9)，就得到了正交曲线坐标系中的梯度算子：

(12)

1.2 正交曲线坐标下单位矢量对坐标的导数

对于柱坐标系有

α1=r,α2=θ,α3=z

(13)

(14)

对应的笛卡儿坐标为

(15)

由式(5)得拉梅系数为

h1=1,h2=r,h3=1

(16)

将式(15)、式(16)代入式(7)，得柱坐标系与笛卡儿坐标系单位矢量之间的关系为

进一步可求出柱坐标系单位矢量对坐标的偏导数：

(18)

同理，对于球坐标系有

α1=r,α2=θ,α3=φ

对应的笛卡儿坐标为

(20)

球坐标系的拉梅系数为

h1=1,h2=r,h3=rsinθ

(21)

球坐标系与笛卡儿坐标系单位矢量之间的关系为

(22)

球坐标系单位矢量对坐标的偏导数为

(23)

2 位移矢量的梯度及几何方程

对于柱坐标系，位移矢量为

(24)

将式(24)代入式(12),有

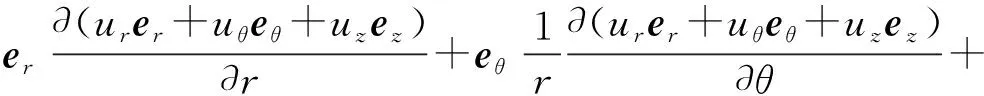
(25)

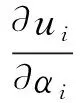
(26)

写成矩阵形式为

(27)

将式(27)代入式(1)，得柱坐标系中的几何方程为

(28)

同理，可得球坐标系下的位移梯度为

(29)

将式(29)代入式(1)中，得球坐标系中的几何方程为

(30)

3 应力张量的散度及平衡微分方程

(31)

从式(31)可以看出，在正交曲线坐标系中要求应力散度，除了求应力分量对坐标的偏导数iσij之外，还要求单位矢量对坐标的偏导数

有了上面的基础，就可以求应力张量散度的具体表达式.对于柱坐标系，根据式(12)，可求得式(31)等号右边第1项的展开式：

(32)

根据式(12)和式(18)，可求得式(31)等号右边第2项的展开式，此时只有i=r、k=θ这种取值组合时计算结果不为0，其他i、k取值时均为0，有

(33)

同样根据式(12)和式(18)，可求得式(31)等号右边第3项的展开式，此时只有i=θ、j=r和i=θ、j=θ这2种取值组合时计算结果不为0，其他i、j取值时均为0，即

(34)

根据式(32)、(33)和(34)，最后有

(35)

再根据式(2)，即可得柱坐标系下的平衡微分方程：

(36)

同理，球坐标系下式(31)等号右边第1项的展开式为

(37)

球坐标系下式(31)等号右边第2项的展开式为(此时只有i=r、k=θ，i=r、k=φ，i=θ、k=φ这3种取值组合时计算结果不为0，其他i、k取值时均为0)

(38)

球坐标系下式(31)等号右边第3项的展开式为[此时只有式(23)中5项偏导数不为0时计算结果不为0]

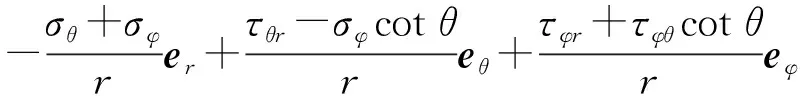
(39)

根据式(37)、式(38)和式(39)，得到球坐标系下的应力张量散度·σ，再带入式(2)，即得到球坐标系下的平衡微分方程：

(40)

4 结语

通过上述推导过程可以看出，利用正交曲线坐标系与笛卡儿坐标系单位矢量之间的关系，以及笛卡儿坐标矢量为常矢量的特性，可以比较容易地推导出正交曲线坐标系中的梯度算子和单位矢量对坐标的偏导数.在此基础上，运用张量的场论基础，通过微分运算，推导出位移矢量的梯度和应力张量的散度，进一步根据弹性力学几何方程和平衡微分方程张量表述形式不依赖坐标系的特性，得到柱坐标系和球坐标系中几何方程和平衡微分方程.与大部分教科书通过几何分析的推导方法相比[3]，张量分析推导方法更加清晰严谨，更具普遍适用性，且本文推导过程所需的张量知识少，可供弹性力学教学和科研参考.