基于4f系统的光学图像加密与解密
盛天爽,蔡乐雨,许 诺,潘永华,丁剑平
(南京大学 物理学院,江苏 南京 210093)
由于光具有高速、高并行度和多密钥自由度(振幅、相位、偏振)的特点,因此光学信息加密成为信息安全领域的重要研究课题.目前有许多基于光学原理的信息加密的报道[1,2],其中对于光学图像的加密则具有重要的实际意义.自从1995年双随机相位编码方法实现光学图像加密[3]被首次提出之后,大量的改进方法相继被发明.但是这些方法都属于对称加密范畴,并且由于加密系统的线性特点,这些加密方法的安全性较低.为解决这一问题,2010年Peng等人首次提出非对称光学加密系统[4],利用在双随机相位编码过程中引入相位裁剪操作,使加密结果仅保留光强信息,实现了加密与解密密钥的不一致性.这一方法在现有的攻击手段下都显示出很高的安全性.
然而,在实际实验解密过程中会遇到解密相位掩膜密钥在光路中难以精确放置的问题,这使得光学解密的效率很低,阻碍了光学加密的实用化进程.因此对于图像加密的研究大多停留在计算机仿真阶段[1,5],有关光学实验的报道很少.本文基于4f系统设计了“对称-非对称混合加密”方法,将光学实验与计算机处理有机结合,降低了实验的难度.结果表明该加密方法具有良好的安全性,且在密度小于0.4的椒盐噪声干扰下具有较高的鲁棒性.
1 实验原理
1.1 阿贝成像原理
阿贝成像原理可以利用4f系统解释.4f系统是由两个焦距为f的全同薄透镜L1和L2组成的光学系统,其中L1的后焦面与L2的前焦面重合,此平面称为傅里叶平面.4f系统的输入面为透镜L1的前焦面,输出面为L2的后焦面.在相干光照射下,4f系统成像可以分为二次衍射.第一次衍射发生在输入面s到傅里叶面s′,通过物的衍射光在L1后焦面上形成夫琅禾费衍射图;第二次衍射发生在傅里叶面s′到L2的后焦面s″,将傅里叶面上夫琅禾费衍射图上各点发出的球面波在输出面上相干叠加得到最终倒立等大的实像[6].该过程本质就是两次傅里叶变换.
(1)
(2)
其中g(x,y)是输入面光场复振幅分布,G(fx,fy)是对应的空间频谱,fx和fy是x和y方向的空间频率,而h(x″,y″)是输出面上光场复振幅分布,其满足h(x″,y″)=g(-x,-y).
1.2 Lee型迂回相位编码
本实验对明文图像在频域进行加密.在4f系统傅里叶面上放置特定的相位掩膜作为密钥进行空间滤波,则最终在4f系统的输出面上可获得模糊的密文.自行设计加密相位函数(密钥)后利用Lee型迂回相位编码方法制作其对应的计算全息图,然后加载在位于傅里叶面上的空间光调制器上.Lee型迂回相位编码的思想是生成一个特殊的光栅,使得该光栅特定的衍射级次能够受所设置的相位函数调制.利用Lee型迂回相位编码制作计算全息图的基本原理如下[7]:
对复函数exp[iφ(x,y)]选取特定个数的抽样点均匀抽样,每个抽样点的函数值对应于复平面上一个向量,如图1(a)所示.在空间光调制器(SLM)上选取4×4共16个像素点称为宏像素.如图1(b)所示.将宏像素沿x轴方向分解成四个部分,分别对应延迟相位0、π/2、π、3π/2,而宏像素y轴方向则保持不变.抽样点函数值对应的向量可分解为
f(a,b)=f1(a,b)r++f2(a,b)j++f3(a,b)r-+
f4(a,b)j-
(3)
其中,r+、j+、r-、j-对应复平面的基矢量,满足
r+=e0,j+=eiπ/2,r-=eiπ,j-=ei3π/2
(4)
投影长度f1、f2、f3、f4是非负实数.因此对于一个抽样点,只要在宏像素的两列中使用投影长度对应的灰度等级表示即可.对每个抽样点进行如上操作,最终在SLM上可制得一幅完整的计算全息图.

图1 Lee型迂回相位编码
(5)
其中fx是x方向的空间频率.显然,负一级衍射光的复振幅分布受到了相位函数exp[iφ(x,y)]的调制,通过空间滤波方法可以将其单独保留.
1.3 对称-非对称混合加密原理
在信息安全领域中有两种普遍运用的加密密码,分别是对称加密和非对称加密.对称加密过程中发送方的加密密钥和接收方的解密密钥相同.而在非对称加密的过程中,发送方利用一个公开的公钥对明文进行加密,而接收方则利用一个与之不同的非公开的私钥对密文进行解密.在本实验过程中,将两种加密方法相结合,称之为“对称-非对称混合加密”,以下对该方法的原理进行简单介绍.
令f为明文,FT(·)为傅里叶变换算子,IFT(·)为逆傅里叶变换算子,PT(·)为相位裁剪操作算子,PR(·)为相位保留操作算子.例如F=FT(f)=|F|exp(i2πφ),则PT(F)=|F|,PR(F)=exp(iφ).根据这一方法,本文设计了如图2(a)所示的加密流程.加密者选定加密相位密钥K,则密文g可以通过如下的加密方法得到
g(x,y)=PT[IFT[K(u,v)·FT[f(x,y)]]]
(6)
同时,加密过程中也产生了解密所需的密钥P:
P(x,y)=PR[IFT[K(u,v)·FT[f(x,y)]]]
(7)
解密流程如图2(b)所示,包含如下两步操作:
g2(u,v)=FT [g(x,y)·P(x,y)]
(8)
f(x,y)=PT[IFT[g2(u,v)·K(u,v)*]]
(9)
显然,密钥K既用于加密明文,又在解密过程中决定解密密钥K*,因此K对应于对称加密过程中的密钥.而解密过程中另一密钥P与K不同,此处K与P分别对应非对称加密过程中的公钥与私钥.至此本方法实现了将对称加密和非对称加密的结合.
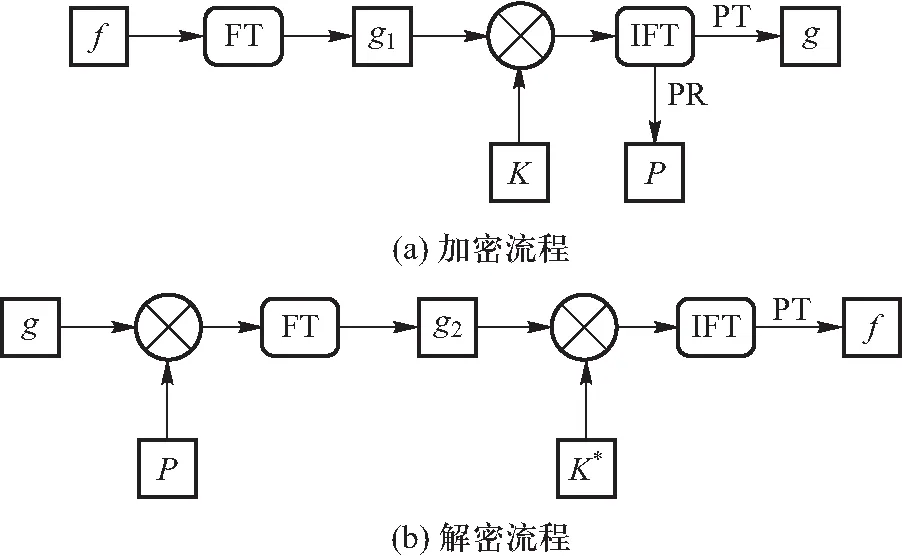
图2 方案流程
值得注意的是,本方法中的密钥P伴随加密过程产生,因此需要通过额外的安全通道传输给接收方.在实验中采用Arnold置乱方法[7]对密钥P进一步加密以提高密钥传输的安全性.事实上密钥P是一个矩阵,对其中的每一个元素pij规定如下的置乱规则:pi′j′=pij,其中下标符合的变换关系为

(10)
式(10)中a和b参数可在通信双方的保密传输协议中进行规定.N为P矩阵的阶数(若P不为方阵则可根据需要添零成为方阵).接收方可通过式(11)所示的下标对应关系将置乱后的矩阵P还原,获得正确的解密密钥P为
(11)
2 加密与解密实验
本文设计了如图3(a)所示的实验光路对加密原理进行验证,实验实物图如图3(b)所示.在一套透镜焦距为200 mm的4f系统的输入面处放置第一个振幅型空间光调制器,加载简单的黑白二值图像作为物体,图像选为1 024 px×728 px的黑色背景,其中央有一白色“光”字,尺寸为64 px×64 px.综合考虑空间频率和空间光调制器的像素个数,本文选择的加密函数K为周期性二元函数:
K(x,y)=2πsin(1 750x)cos(1 750y)
(12)
在函数exp[iK(x,y)]的相位调制下,加密所得密文会在x和y两个方向呈现出较大程度的扭曲,因此可以充分隐藏明文信息.本实验利用1.2节介绍的Lee型迂回相位编码原理,将该函数制作成计算全息图,并加载在位于傅里叶面的第二个振幅型空间光调制器上.以上两个空间光调制器像素均为1 024 px×728 px(像素大小26×26 μm2),位于输出面上的CCD相机像素是1 024 px×1 280 px(像素大小5.6×5.6 μm2),当物体大小选择合适时总可以在CCD相机上接收到完整的密文.由(5)式可知负一级衍射图样是最终所需的加密结果,但两次透镜的傅里叶变换作用导致其最终是倒立像.为此,将CCD相机接收图像设置成自动旋转图像180°,如图4所示得到的白框内衍射图样即为加密结果.另外,为了防止零级像将明文泄露,实际实验中在每台空间光调制器前后各加了一个偏振片,如图3(b)所示,通过旋转偏振片到合适的角度可以将零级像消去.由于CCD相机只能接收到光强信息,且光强正比于复振幅分布的强度的平方,所以相位剪裁的操作可以自动完成.为了将相位保留生成解密密钥P,可以对原始输入图像利用式(5)进行计算,从而获得相位分布.由于得到的P矩阵为1 024×728阶矩阵,为了满足1.3节介绍的Arnold置乱的要求,必须对P矩阵补零使之成为方阵后再进行Arnold置乱,最终完成加密流程.

实验光路图

图4 加密前后对比
为了解决实验时共轭密钥K*所对应的相位掩膜难以在光路中精确放置问题,本文自行设计了解密程序,使得解密操作可由计算机精确执行,大幅度提高了解密效率和质量.该计算机程序不仅可对密钥P进行恢复,而且可自动过滤出CCD接收图片中正一级加密图样.通过图5所示的滤出的一级密文可知其基本隐藏了明文信息.将密文图像强度信息结合利用式(11),恢复后的密钥P所代表的相位分布就可以重建出一级衍射光场.之后计算机可以结合K*和P,并根据(8)、式(9)对重建的复振幅进行计算,最终获得解密像.图5所示的解密结果表明其与明文高度相似,但是其亮度不及明文,具体原因是一级衍射场分配到的能量小于入射光总能量,因此光强有所下降.另外,由于程序解密计算的原理完全基于解密相位掩膜精确放置的理想解密光路,因此解密难度降低而且不会引入环境噪声.

图5 解密前后对比
3 性能分析
原始明文与解密结果之间的相似度可以通过两幅图像的相关度定量表示.相关度CC的定义是
(13)

(14)
其中0≤α≤1,rand(-2π,2π)代表(-2π,2π)区间内均匀分布的随机数.正确度α反应了假想的窃密者在窃听时对密钥引入的随机噪声,正确度越高则噪声越小.


图6 CC值与K*密钥正确度关系
另外,本文还证明了使用密钥P可使加密方法的安全性进一步提高.假设窃密者同时截获了加密图片和被加密的密钥P,但由于未知保密传输协议中的置乱参数而无法将密钥P正确恢复,此时如果窃密者使用强力攻击破译置乱参数,其解密结果如图7(a)所示.而图7(b)(c)分别表明窃密者没有截获密钥P而直接对密文进行强力攻击,和窃密者只通过密钥K进行解密时都无法获得正确的解密结果.同时通过计算可得这些解密结果与明文之间的相关度CC值都非常低,这进一步证明了对称-非对称混合加密方法具有很高的安全性.

置乱参数错误 强力攻击 只使用密钥K解密图7 错误解密结果
考虑到实际传输时密文会因受到干扰而引入噪声,在这种情况下能否正确还原出明文考验的是加密方案的鲁棒性.本文利用计算机模拟方法在密文中加入椒盐噪声,噪声密度从0至0.45每隔0.05取一个值,随后利用正确的解密方法进行解密,利用式(13)计算不同椒盐噪声密度影响下的解密结果和原始图像之间的相关度.最终用折线将数据点连接,得到图8.结果表明在密度低于0.4的椒盐噪声影响下,解密结果与明文之间的相关度均超过0.8,说明本加密方法在较低噪声下具有较高的鲁棒性.

图8 椒盐噪声影响下的加密方案鲁棒性测试
最后需要指出的是,对密钥K改进可以进一步提升加密安全性.例如将K设置为随机相位函数.理论上同样可以利用该随机相位函数对应的计算全息图对明文图像的频谱进行相位调制,这会使得CCD接收到的加密图案更接近白噪声,从而提高加密的安全性.但是这种随机衍射会导致加密图像向空间各个方向散射,使得无法通过CCD接收到完整的加密图像.解决该问题的方法是换用纯相位调制型空间光调制器直接对频谱进行相位调制.由于目前受器材限制,无法对此进行实验验证.如果条件允许,这不乏是一种更安全的加密手段.
4 结语
本文基于4f光路设计了一套对称-非对称混合加密系统.该系统有K与P两幅密钥.首先通过Lee型迂回相位编码生成密钥K对应的计算全息图,并将其放置于4f系统的傅里叶面上对明文图像进行频域加密,最终使用CCD相机接收加密密文.与此同时利用相应公式对明文计算生成密钥P,并通过Arnold置乱操作对密钥P进行加密从而实现保密传输.利用自行编写的计算机程序进行解密操作,大幅度提升解密的效率和质量.实验表明该加密方法具有较高的安全性,同时也证明了本方案在密度小于0.4的椒盐噪声干扰下具有较好的鲁棒性.同时本实验设计也为光学加密实验方面的研究开辟了新的思路.

