光子筛:研究进展及空间应用前景
熊玉卿,李 坤,王 瑞,王志民
(兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000)
0 引言
光子筛(Photon Sieve)是一种新型衍射光学元件,其概念于2001年由德国Kiel大学的Kipp等[1]首次提出。光子筛是在菲涅尔波带片的基础上发展起来的。
自从2001年光子筛的概念被提出以后,各国研究人员针对提高衍射效率、展宽成像光谱、提高分辨率等需求开展了对光子筛成像特性的研究,并制作了多种小型光子筛[2-6]。这些研究成果一方面证明了光子筛的成像优势,另一方面也暴露出光子筛成像特性的一些缺陷。首先,由于利用透光小孔取代菲涅尔波带片的透光环带,降低了对入射光的利用率,导致衍射效率低;其次,作为衍射光学元件,光子筛的色差特性非常明显,使得成像带宽很窄。要实现光子筛的实际应用,必须重点研究解决上述问题。
本文将对光子筛与传统衍射光学元件进行对比,介绍国内外光子筛在计算理论和方法、构型设计、制作技术以及应用方面的发展现状,并分析光子筛的空间应用前景。
1 光子筛的成像机制
光子筛与菲涅尔波带片的区别在于,菲涅尔波带片是由一系列明暗相间的同心圆环组成,而光子筛是将菲涅尔波带片的明暗环带替换为一系列按一定规律分布的小孔,如图1所示。
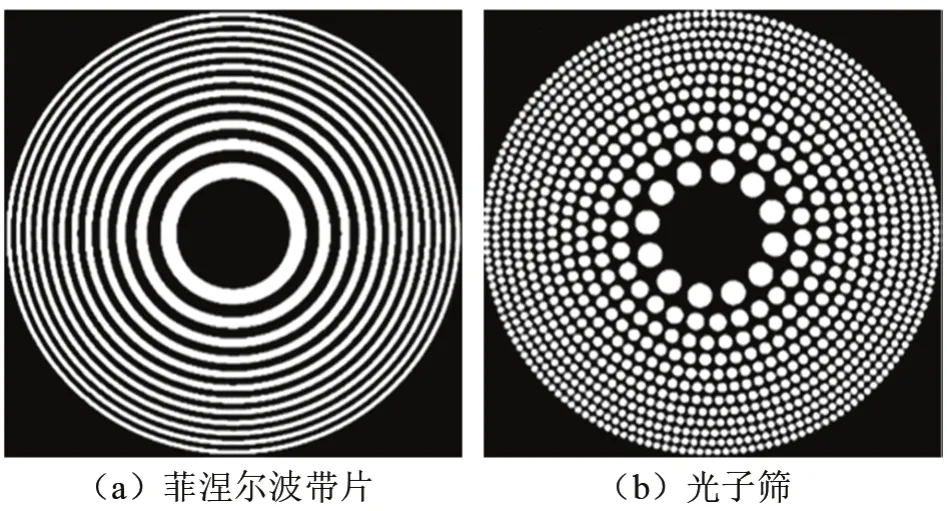
图1 菲涅尔波带片和光子筛对比Fig.1 Comparison of fresnel zone plate and photon sieve
光子筛的小孔具有下列特点:第一,小孔的尺寸取决于光子筛的工作波长,一般为微米或纳米量级;第二,小孔的位置须满足如下要求,即光波通过所有小孔中心到达焦点的距离与光波通过光轴到达焦点的距离之差(称为光程差)应是对应波长的整数倍。这样,通过光子筛每一个小孔的衍射光,在光子筛后的同一位置均为同相相加。图2是光子筛的成像机制示意图[1]。
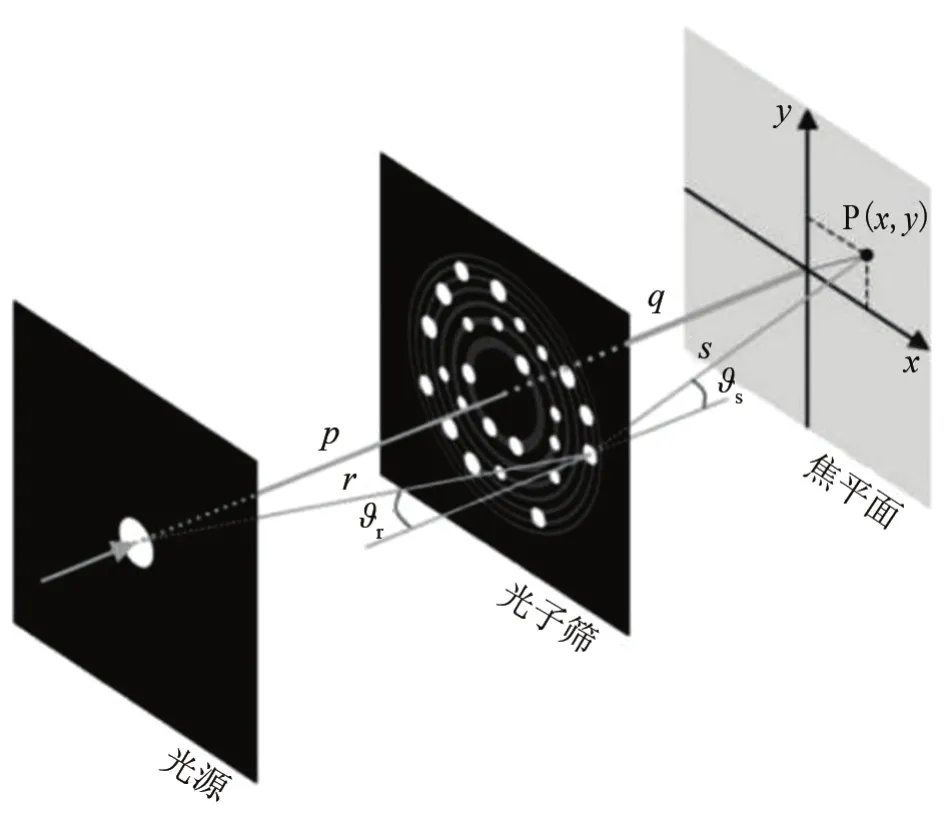
图2 光子筛的成像机制示意图Fig.2 Schematic diagram of imaging mechanism of photon sieve
假定一个光源距光子筛的距离为p,光波到达光子筛平面后,通过光子筛在距离为q的焦平面上一点聚焦。为了简化,假定光源和像均位于光轴上(实际上,在光子筛系统中,可以实现光源离轴或像离轴或者两者同时离轴)。为获得清晰的一级聚焦,从小孔中心到焦点的光程应该是波长λ的整数倍。因此,小孔应位于以光轴为中心、由式(1)决定的rn为半径的圆上:

式中:λ为光波波长;n为正整数。
选取数n和φ(0<φ≤2π)之后,即可以获得以(rn,φ)为中心的小孔位置分布。
利用菲涅尔-基尔霍夫衍射理论可计算图2中P点的光强振幅:

式中:A为距光源单位距离处的光强振幅;r、s、ϑr和ϑs的含义分别如图中所示,,k=2π/λ。对所有的小孔进行积分,即可获得P点的总振幅。
根据式(2)计算得到的单个小孔对焦平面处振幅的贡献与d/w的函数关系如图3所示。图中,位于小孔内的白色区域产生的相长干涉和黑色区域产生的相消干涉对聚焦的贡献分别用灰色的实线和虚线表示,不同直径d、中心均位于宽度为w的透明区中的小孔(插图中A、B、C)在焦平面处产生的光强振幅总和用黑色实线表示,中心位于不透明区的小孔(插图中D)在焦平面处对光强振幅的贡献用黑色点线表示。

图3 小孔尺寸和位置对聚焦的贡献示意图Fig.3 Schematic diagram of contribution of hole size and position to focusing
单个小孔在焦平面处产生最大振幅值对应的小孔直径大约为1.53w、3.51w、5.51w……等值(对应焦平面处1级、3级、5级衍射)。当小孔中心从透明区移到不透明区时,焦平面处振幅值会发生正负颠倒,因此直径约为3.5w、7.5w……等的小孔中心应该位于不透明区,以在焦平面处获得相长贡献(图3插图中D)。
波带片的空间分辨率Δx取决于最外圈环带的宽度wmin:Δx≈wmin(1级衍射);当工作在更高的m级(奇数)衍射时,也可以获得强度降低(~1/m2)的小光斑(~1/m)。但是,对于光子筛来说,即使是1级衍射,空间分辨率也可以小于最小的孔径dmin。事实上,它受限于所对应波带片的最外层环带的宽度。这个有效最小宽度取决于d/w的最大值:
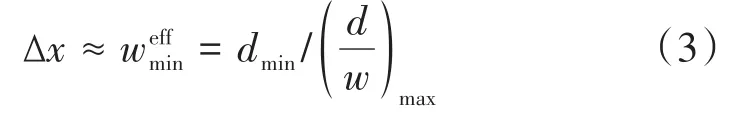
图4是计算得到的光子筛和对应波带片的光强分布对比,图中实线代表光子筛,虚线代表菲涅尔波带片,两种衍射光学元件的最小结构尺寸均为30 nm。从图中可见,光子筛的聚焦光斑明显小于所对应的菲涅尔波带片的聚焦光斑(图4(a)为聚焦光斑在焦平面上的强度分布,图4(b)为聚焦光斑在轴向的强度分布),可以看出,相比于菲涅尔波带片,光子筛的聚焦光斑具有更强的旁瓣抑制能力,可以显著提高分辨率。
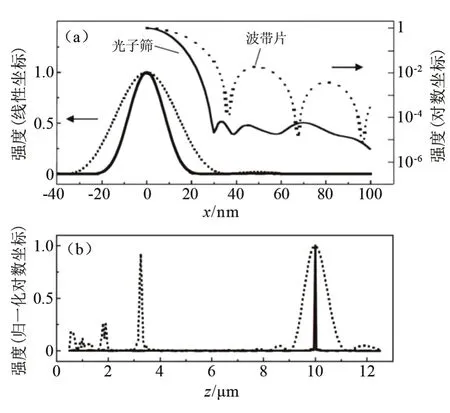
图4 光子筛和波带片的计算光强度对比Fig.4 Comparison of calculated light intensity between photon sieve and zone plate
作为一种新型衍射光学元件,光子筛除了具有传统衍射光学元件可以对超短波长成像的特点,还可以有效抑制高阶衍射和旁瓣,提高成像质量。研究表明,即使光子筛小孔的尺寸大于对应的菲涅尔波带片环带的宽度,但不超过一定范围时,成像质量不受影响。这可以降低光子筛的制作难度,同时有助于增加系统的光通量。
2 光子筛的计算理论和方法
光子筛的概念被提出之后,首先在计算理论和方法方面得到迅速发展。
Kipp在提出光子筛概念时,采用的分析理论和方法是传统的菲涅尔波带片理论和菲涅尔-基尔霍夫衍射积分。德国Hagen大学的Cao等[3-4]对光子筛模型作了系统而全面的分析。在他们的早期工作中,同样采用菲涅尔波带的概念和菲涅尔-基尔霍夫衍射集成数值计算,提出了一种用于低数值孔径光子筛分析与设计的近轴远场模型,并将模型扩展,使之可以应用于工作在软X射线波段的高数值孔径光子筛的非近轴情形分析与设计。后来,他们利用标量衍射理论详细分析了光子筛的理论光强分布,讨论了光子筛在焦平面上和沿光轴方向上的光强分布特性。根据小孔的小尺寸特征,利用精确的瑞利-索末菲衍射公式积分函数的局域泰勒展开,推导出了应用于远场小孔的非傍轴表达式,根据这个表达式和线性叠加原理,建立了应用于高数值孔径光子筛的非傍轴远场模型,给出了光子筛的筛孔尺寸、筛孔半径位置的确定条件。
新加坡国立大学Huang等[7]提出一种可见光波段光子筛的复合设计方法,利用耦合模理论[8]描述小孔出口平面上的电场,利用多级展开法[9]描述出口平面上电场的远场衍射。设计了一种由超高密度亚波长小孔构成的非周期复杂结构,可以精确调控光,实现无孪生像、高衍射效率的全息图。另外,利用非周期随机分布光子筛,可以将光线聚焦成尺度为0.32λ的光斑,实现高分辨率聚焦。这种针对亚波长小孔远场衍射建模的复合设计方法很容易扩展到任意形状光子筛(如矩形、椭圆形、环形和三角形等)的设计,对于为实现光的空间振幅、相位和极化调制而进行的单元元素的几何排列具有鲁棒性和通用性。随机分布光子筛具有偏振无关性、超薄平面性、高的场均匀性以及高衍射效率等优点,可以应用于集成光子学和光束整形等。
苏州大学Zhao等[10]提出一种基于波前编码的光子筛宽带衍射成像技术,在光子筛的前端置入经过特定设计的非球面位相元件,对光子筛的入射波前进行编码,组成分离式波前编码光子筛成像系统。理论研究表明,该系统的调制传递函数和点扩散函数对入射波长不敏感,因而可以展宽光子筛的工作带宽。在此基础上,采用光子筛实现波前编码,将衍射聚焦和波前编码两个功能集成在一个单一的光子筛上。通过对光子筛小孔的空间分布进行调制,使得在很宽光谱范围内的入射光产生一致的聚焦效果,降低衍射器件对波长的敏感性,实现光子筛在宽光谱条件下的清晰成像。
中国科学院长春光机所Liu等[11]针对大尺寸光子筛提出一种小孔环衍射模型,以提高对光子筛聚焦特性的计算效率。通常情况下,对光子筛的计算是以每个小孔为单元单独计算的,这对于小孔数量巨大的大尺寸光子筛来说,计算量将非常大。基于单个小孔的非近轴远场模型,对于小孔尺寸相同、在环带上均匀分布的小孔,小孔环衍射模型将同一环带上的所有小孔作为一个整体来计算。计算结果表明,该模型可以实现对光子筛聚焦特性的快速准确计算。
在光子筛的设计中,为了抑制衍射中的次级主最大,消除焦平面上的背景光,通常采用不同的窗函数对光子筛的结构进行调制。窗函数是数字信号处理中对信号进行截取的截断函数。用窗函数可以调制光子筛的小孔数量和分布,使通过光子筛的光波绝大部分能量集中在主焦点上,而在主焦点以外的区域,光强迅速衰减。这种调制方式通常也被称为切趾[12-16]。
香港中文大学Cheng等[12]提出一种泽尔尼克切趾光子筛结构。这种光子筛是基于切趾光子筛和泽尔尼克相衬两个概念的结合,利用切趾光子筛的高分辨率和泽尔尼克相衬的高成像对比度,通过在一个切趾光子筛上进行选择性区域移位,实现±π/2的相移。根据点扩散函数对这种切趾光子筛进行的聚焦特性分析表明,通过调节窗函数的切趾因子σ,可以显著抑制旁瓣,但付出的代价是主瓣宽度会略微展宽。将这种光子筛作为高分辨率相衬X射线显微镜的物镜,与同步辐射光源相结合,可实现X射线对弱吸收材料的高空间分辨率和高相衬成像。
中国科学院微电子所Xie等[13-14]提出一种改进的三参数凯撒切趾窗函数,用于调制应用于硬X射线波段的光子筛的小孔密度,并分析了光子筛微纳结构中的波导传输特性。理论分析表明,波导效应可以抑制高阶衍射效应的出现,而凯撒窗函数中额外的参数可以增加调制半高宽和信噪比的自由度。经过90°相移后的硬X射线光子筛可以获得很好的信噪比,同时,光子筛的厚度对半高宽没有影响,这在一定程度上降低了对光子筛制作的要求。
中国科学院长春光机所Liu等[15]提出一种多区域切趾光子筛设计方法。利用标量场框架下的小孔环模型,将一个光子筛分成多个环形区域,对每个区域采用不同的窗函数。研究了区域数量、窗口函数和小孔数量对光子筛衍射特性的影响。研究发现,通过调节小孔尺寸,衍射效率可提高25.5%。
综上所述,目前的光子筛设计基本都以标量衍射理论为计算依据,这种方法的优点是计算过程简单,无须考虑振动的方向,缺点是当小孔直径较小时,计算误差较大。因此,为获得准确的计算结果,应当考虑结合矢量衍射理论来进行光子筛的设计计算。切趾从本质上讲是一种优化设计方法。
3 光子筛的构型设计
3.1 振幅型光子筛
振幅型光子筛是光子筛的最基本形式,是将对应菲涅尔波带片的透光环带用小孔代替,小孔直径等于环带宽度,小孔的中心位于波带片透明环带的中心,同时,须满足光波通过各小孔中心到达焦点与通过光轴到达焦点的光程差为波长整数倍的条件。这样,入射光通过所有小孔到达焦点时,光强满足同相位叠加条件,焦点处的光强振幅会大幅增强。因此称为振幅型光子筛。
3.2 相位型光子筛
相位型光子筛[17-18]与振幅型光子筛的区别是,将振幅型光子筛中的不透明材料基底替换为吸收较小的相位型材料,利用圆槽或者圆柱形结构,在相邻的透光环带和不透光环带之间引入相位差π,这样,经过小孔的光和透过材料的光对焦面处光场的贡献均为正,达到提高光子筛光能利用率的目的。但是,相位型光子筛不能提高光子筛的聚焦性能。
美国空军学院Anderson等[19]提出一种“负孔”型光子筛。振幅型光子筛的小孔中心位于透明环带中心线上,“负孔”型光子筛的小孔中心则位于不透明环带中心线上。由于允许的小孔直径可以达到对应环带宽度的3倍以上,这种设计可以获得更大的孔径而不必损失光通量,同时,降低了光子筛的制作难度。Anderson等利用“负孔”型光子筛制作了直径10 cm的空间望远镜主镜,并采用另一个衍射元件进行色差校正,使工作带宽达到40 nm。
浙江大学Hou等[20]提出一种二元光子筛结构。该光子筛结合了振幅型光子筛和“负孔”型光子筛,在对应透光环带及不透光环带上均分布有大量透光小孔,如图5所示,两种环带上的小孔存在一个π的相位差。对聚焦能量、透射波前等进行的测量表明,相对于振幅型光子筛,二元光子筛的透射能量和聚焦光点的能量占总入射能量的比例有较大提高。

图5 振幅型光子筛和二元光子筛对比图Fig.5 Comparison of schematic diagram of amplitude photon sieve and binary photon sieve
中国科学院光电技术研究所唐燕等[21]设计了一种准相位型光子筛。与二元光子筛类似,这种光子筛同样在透光环带及不透光环带上都分布有小孔。不同之处在于,准相位型光子筛的透光环带和不透光环带之间不需要π相位差,是通过调节不透光环带上小孔的直径,对焦点处的相位分布进行调制的。由于对基底没有特殊要求,准相位型光子筛可以降低光子筛的制作难度,而且可获得大的数值孔径。
3.3 全透明型光子筛
振幅型光子筛是在不透明基底上加工小孔形成的,因此,其透射率很低,一般不超过25%。较低的透射率阻碍了它在很多领域的应用,如卫星遥感。为了克服振幅型光子筛固有的缺点,美国科学系统与应用公司Sun等[22]提出了全透明光子筛,在透明薄膜上加工光子筛小孔,透明薄膜为具有要求折射率的完全透明材料。为使光线聚焦在焦点处,透明材料的厚度δ和折射率m须满足如下条件:

式中:λ为光在自由空间中的波长;j=0,1,2,3,…。式(4)表示通过小孔的光线和通过薄膜的光线的相位差。根据式(3),可以得到薄膜材料的光学厚度D:

选取折射率合适的材料,可以显著提高光子筛的透射率。即使实际材料的折射率不能刚好等于m,折射率相近的材料仍然可以改善光子筛的透射率。由于全透明型光子筛具有高的透射率,因此适合制作与多层二元相移菲涅尔波带片[23]相似的多层光子筛,可以得到大于50%的聚焦效率。
3.4 反射型光子筛
在全透明光子筛的基础上,研究者提出了反射型光子筛的概念[24-25]。反射型光子筛是在全透明光子筛背面增加一个反射镜构成的,透明薄膜的光学厚度为入射波长的1/4(相当于一个减反射膜层),这样的设计使得从小孔中反射出来的光和经过透明薄膜反射出来的光具有一个180°的相差,入射到镜面上的光被反射后聚焦到焦点上。根据模拟结果,这种反射型光子筛具有最高100%的反射率和最高50%的聚焦效率。这种器件的功能类似于一个凹面聚焦镜,但可以保留光的相位特征(如具有轨道角动量的光)。它还具有优异的波长选择性,这样可以在焦点处排除大部分不需要的光。一层很薄的透明薄膜在遥感系统的光路中就可以同时起到透镜和光栅的作用,很适合于在紧凑的光学仪器如卫星遥感仪器中实现对光的调控。美国NASA的研究人员将反射型光子筛应用于LIDAR系统中,成功将所需的信号从背景太阳光噪声中分离出来[26]。
3.5 分形光子筛
由于光子筛本质上是一种衍射光学元件,受到严格的干涉和衍射物理机制的限制,其成像会受到色差的严重影响。因此,传统光子筛只能在设计的单一波长成像,不能满足一些宽光谱成像的需求,限制了光子筛的应用。
西班牙瓦伦西亚理工大学Giménez等[27]和美国宾夕法尼亚州立大学Liu等[28]分别提出了分形光子筛的概念,如图6所示,拓展焦深并减小衍射元件对波长的敏感性以降低色差。

图6 分形光子筛Fig.6 Schematic diagram of fractal photon sieve
这种分形光子筛在光轴方向对每一个波长均产生一系列次焦点,不同波长的次焦点在同一成像平面上可以相互叠加,从而拓展焦深和消除色差。但是,分形光子筛具有能量利用率低、分辨率低、背景杂散光强等缺点,不利于成像。
美国佛罗里达大学Chung等[29]采用分区的办法实现了光子筛对两个不同波长的聚焦,如图7所示。但是,该光子筛只能对设计的两个波长成像,不能满足宽光谱成像的要求,且两个波长之间相互干扰,具有较低的衍射效率。

图7 双波长光子筛Fig.7 Dual wave length photon sieve
苏州大学Chen等[30]为满足超大尺寸可见光波段光子筛设计需求,提出一种多区域光子筛结构,将一个光子筛沿径向由内向外分成若干个环状区域,在同一个环状区域内,对不同环带的小孔采用相同的放大倍率,对不同的环状区域则采用不同的放大倍率,使所有小孔尺寸都在最佳衍射范围内。其设计原理同时基于相匹配和区域内小孔总面积匹配。对多区域光子筛结构和传统单片结构光子筛的聚焦特性如能量效率和旁瓣抑制等进行了对比,结果表明,相同数值孔径的多区域光子筛的聚焦特性要优于单片结构光子筛。对该方法加以扩展,提出了一种依据小孔尺寸和每个环上小孔密度的环对环设计新概念,应用于超大尺寸、高数值孔径光子筛的设计,可以获得优异的旁瓣抑制性能,提高光子筛的分辨率。该方法使得大面积、大数值孔径光子筛的制作难度显著降低。
3.6 斐波那契光子筛
中国科学院上海光机所Zhang等[31]将斐波那契数列应用于光子筛的设计,提出斐波那契光子筛的概念[32]。传统的光子筛小孔中心位于菲涅尔波带片的透明环带上,斐波那契光子筛的小孔中心则是位于根据二元非周期斐波那契数列确定的斐波那契环带上[33]。
基于惠更斯-菲涅耳原理,利用数值仿真分析了斐波那契光子筛的聚焦特性。结果表明,当单色平面波通过斐波那契光子筛时,可以获得两个轴向焦点,其焦距比约为黄金分割比。当筛孔直径等于所在环带宽度的1.165倍时,两个焦点处的光强相等。利用高斯切趾技术,对设计的斐波那契光子筛筛孔数量进行调制,可以在两个焦平面上都获得更高的横向分辨率。
上海光机所王松贤等[34]研究了另外一种可获得双焦点的希腊梯子光子筛,希腊梯子光子筛的编码方法和斐波那契数列编码类似,都是应用数列形成规律对光子筛小孔中心所处的环带进行设计。采用数字全息的方法对由希腊梯子构造的双焦点光子筛进行聚焦特性的研究,利用离轴全息光路,通过一次实验即可获得离焦处的复振幅分布,再通过衍射数字计算,可以得到器件的焦距以及远场衍射的焦斑分布。
3.7 复合型光子筛
振幅型光子筛是将菲涅尔波带片所有的透明环带用小孔替代,如果只将一部分波带片透明环带用小孔替代,而保留另一部分透明环带,这种由波带片和光子筛组合的衍射元件通常被称为复合型光子筛[35]。复合型光子筛在提高透射率的同时,也可减少光子筛的加工制作数据量。复合型光子筛的光子筛部分实现对信噪比的提高,波带片部分则使透射率比普通光子筛高,同时数据量较少,对于大孔径光子筛的制作具有优势。但是,这种复合型光子筛也会损失光子筛的部分优点,例如,会降低成像质量。因此,必须根据实际需求,进行折衷考虑,以获得满意的成像效果。
4 光子筛的制作技术
最早的光子筛是利用镀铬的石英玻璃制作的,首先在石英玻璃板上沉积铬膜,再利用电子束曝光在铬膜上加工出设计好的图形。2005年,美国空军学院Anderson等[2]报道了利用镀铬石英片制作的光子筛,口径为100 mm,工作波长532 nm,最小孔直径10 μm;随后在2006年,又制作了同样口径和工作波长的负孔光子筛[19]。
在国内,中国科学院光电技术研究所在2006年制作了口径为30 mm的镀铬石英玻璃光子筛[36],最小孔直径5.6 μm。2010年,中国科学院微电子研究所在镀铬石英玻璃上制作了口径为17.75 mm的复合型光子筛[35],其半径1/3以内的中心部分为波带环,外部2/3为小孔。
2006年,为满足空间对大孔径轻质成像系统的需求,Anderson等[37-38]开始研究薄膜型光子筛,先后研制了三种不同基底的薄膜型光子筛,其中一种基底为美国Nexolve公司研制的LaRC-CP1超薄聚酰亚胺薄膜,LaRC-CP1具有质量轻、韧性好、可卷曲等优点,还具有接近于零的热膨胀系数,用它制作的光子筛非常适合于空间应用。
薄膜型光子筛采用光刻技术制作,具有易复制、工艺简单的特点。Anderson等[37]采用的制作薄膜型光子筛的流程如图8所示。在薄膜基底上蒸镀一层铝膜,在铝膜上涂AZ1518型光刻胶,基底、铝膜和光刻胶的厚度分别为10 μm、200 nm和2 μm。将预先利用电子束曝光制作好的镀铬石英玻璃光子筛掩模紧贴在光刻胶上,采用紫外线曝光,将光子筛图形转移到光刻胶上,然后移除掩模,刻蚀曝光后的光刻胶和铝膜,最后去除残余的光刻胶,便可得到薄膜型光子筛。利用一块掩模,即可批量生产薄膜型光子筛,与传统的光学元件生产方式相比,可大幅缩短生产周期。
光子筛的其他制作方式包括激光束直写、电子束直写、聚焦离子束直写等。对于尺寸较小的光子筛来说,光刻技术是目前采用的主要技术手段。但随着光子筛尺寸的不断增大,或者要在非平面上制作光子筛时,光刻技术将不能满足要求,须探索其他可加工尺寸大、控制更为灵活的制作技术。
5 光子筛的空间应用
美国在光子筛的应用方面开展了多个项目研究。美国国防高级研究计划局(DARPA)于2010年开始开展薄膜光学成像仪实时利用(Membrane Optic Imager Real-Time Exploitation,MOIRE)项目的研究[39-40]。这是一个大口径衍射光学成像技术应用研究项目,旨在突破衍射薄膜、大型可展开支撑结构、星上薄膜压缩和展开等关键技术,为开发高分辨率衍射成像提供技术支持。
MOIRE项目将实现大口径、轻质量及可折叠展开的低成本高分辨率成像的望远镜系统,如图9所示。系统由物镜和目镜组成,物镜为薄膜型光子筛,项目由美国鲍尔宇航公司承担。MOIRE项目的第一阶段已于2011年9月份完成,完成了初步设计,验证了薄膜型衍射光学成像器件的成像性能;第二阶段主要对整个系统进行地面验证,包括机械设计、全光路测试、环境对系统性能影响等,最终要确保整个系统可以实时获得场景数据;目前项目处于最终阶段,将综合考虑环境、材料等对系统的影响。该系统具有很好的成像性能,还将大幅度降低重量及制造成本,对空间望远镜系统的发展具有重要意义。

图9 采用光子筛作为物镜的地球静止轨道高分辨率成像望远镜系统Fig.9 Geostationary orbit high resolution imaging telescope system using photon sieve as objective lens
2012年,DARPA又开展了军事行动空间使能效果(Space Enabled Effects for Military Engagements,SeeMe)研究计划[41],目的是利用低成本小卫星星座和光子筛衍射成像等新技术,改变美国长期依赖于高成本大型侦察卫星获取地面图像信息的现状。2018年,Raytheon公司向DAPRA交付了第一颗SeeMe卫星[42]。SeeMe卫星项目的最终目标是建设价格可承受的小卫星星座,使地面作战单元可以利用手持设备,直接从小卫星获取精确定位环境的实时高分辨图像信息。
SeeMe项目包括两个主要的关键技术领域。其一是采用非宇航级商业部件,以非连续方式制造卫星,并满足快速制造和低成本的要求;其二是利用可展开射频和成像孔径,使光电系统以最低的成本和质量达到成像传感器性能最高,实现与地面装备直接通信,满足快速响应成像需求。
2014年,以美国空军学院为主,合作方包括美国国家侦察局、DARPA、美国空军科学研究办公室、空军技术学院、NASA、MMA设计公司以及空军研究实验室等多家单位,开始研制“猎鹰卫星-7”微卫星[43-45],首次探索将薄膜型光子筛作为望远系统载荷主镜,采用波音公司制造的殖民地II 3U卫星平台,尺寸约为30 cm×10 cm×10 cm,质量5 kg,主载荷为一台口径200 mm、焦距1 000 mm的薄膜型光子筛衍射主镜,工作波长为656.45 nm的H-alpha,有效视场0.008°,主要用于观测太阳活动,具备在450 km轨道高度对地面以1.8 m分辨率成像的能力。如果“猎鹰卫星-7”能够验证薄膜型光子筛的高分辨成像能力和空间可靠性,将使低轨道卫星在保持高分辨率的前提下实现轻量化甚至超轻量化。
综上所述,美国的光子筛技术空间应用发展遵循了理论研究、地面试验、低轨验证及应用、高轨应用的路线,逐步实现光子筛技术的实用化,参加各单位按不同分工开展研究。
6 总结
对薄膜型光子筛的研究及初步应用表明,光子筛在构建大口径空间光学元件上具有显著的优势。首先,与菲涅尔波带片相比,光子筛的所有非图形区域是连续一体的,这样,可以将光子筛直接加工在薄膜上而不需要基底或其它支撑结构;而且,光子筛的最小尺寸通常大于所对应的特征波长,这可以降低光子筛的制作难度;其次,光子筛可以抑制高阶衍射和旁瓣效应,其空间成像分辨率可以突破瑞利衍射极限的限制,从而提高衍射元件的成像质量,这是波带片难以实现的;第三,光子筛能对各种波长的光束成像而不受材料限制,因此可成像的光谱范围宽,可探测普通光学望远镜和基于菲涅尔波带片的望远镜探测不到的短波波段;最后,薄膜型光子筛质量轻、易于折叠和展开,有利于大口径光学元件在卫星上的装载以及卫星的发射。可见,光子筛为大口径、高分辨、可折叠展开的轻质空间光学元件提供了技术途径,将促进大型衍射光学元件未来在空间的应用。
但是,与光子筛优点并存的,是实际应用中必须解决的缺点和局限性。首先,光子筛对入射光的利用率很低,导致衍射效率低;其次,光子筛的色差特性非常明显,使得成像带宽很窄。目前针对光子筛的设计也是在各指标之间进行折中,例如,目前尚无法同时实现高分辨率、高衍射效率和宽带成像。若要光子筛达到实用化水平,还必须进一步开展研究。另外,和传统透射/反射式光学元件相比,尽管光子筛对形位偏差的容忍度要高得多,但大口径薄膜型光子筛的空间面型精度保持,仍是实际应用须重点考虑的问题。未来可采取一种多区分块设计制作并在太空进行拼接的方式,以降低光子筛面型精度的保持难度。

