电喷推力器稳定域研究与性能测试
张 开,索晓晨,黄潇博,李自学,汪 典,贾宏宇,匡双阳,宋培义*,涂良成,2*
(1.华中科技大学物理学院引力中心 基本物理量测量教育部重点实验室引力与量子湖北省重点实验室 精密重力测量国家重大科技基础设施,武汉 430074;2.中山大学物理与天文学院(珠海校区),广东 珠海 519082)
0 引言
空间引力波探测计划[1-2]目标是在太空中部署多颗相同卫星,构建天基激光干涉引力波天文台,利用无拖曳控制系统解决高精度空间惯性基准问题以及大尺度、高精度分布式系统的一致性问题。无拖曳控制技术是利用微推力器产生的推力来补偿航天器搭载惯性传感器进行检测时受到的扰动力,使检验质量不受非保守力影响而处于自由落体运动状态。无拖曳控制是空间精密测量卫星平台的核心技术,是空间基础物理,微重力测量,地球科学与卫星导航等超高精度试验研究的关键技术之一。2016年,欧空局主导的空间引力波探测计划验证卫星LISA Pathfinder搭载了两款微牛顿量级推力器作为无拖曳控制的推力力学执行装置,分别为冷气微推力器以及基于场发射效应的电喷微推力器[3],并完成了3 000 h在轨测试,初步验证表明,两款推力器性能可以满足任务要求。电喷微推力器是20世纪60年代起NASA研究发展的一种新型电推力器,其发射过程在微米级泰勒锥尖上进行,发射电流/推力受电压和工质流量控制,具有推力下限低、精度高、结构简单、功耗低、比冲高的性能优势,适用于微纳卫星轨道维持、深空探测、高精度无拖曳控制等航天任务。目前,国内外多家研究机构针对不同航天使用场景中的电喷微推力器开展了持续性研究工作,包括美国麻省理工学院[4]、加州大学洛杉矶分校[5]、加州大学欧文分校[6],欧洲的洛桑理工[7]、伦敦大学[8]、伦敦玛丽女王大学[9]等。我国对电喷推力器的研究始于21世纪初[10],上海交通大学[11]、北京航空航天大学[12]、中北大学[13]、北京理工大学[14]、上海空间推进研究所[15]、北京机械设备研究所[16]以及兰州空间技术物理研究所[17]等高校与科研单位分别针对毫牛级、高比冲、连续可调型电喷推力器进行原理探索与型号攻关。2019年,航天科工二院206所应用物理技术中心研制的离子液体微电推力器成功完成多次在轨点火试验[18]。2021年,“基于精密反馈控制的微牛级推进技术”重点研发计划项目启动。该项目将场致发射电喷推力器设定为研究方案之一,目标是为实现工程样机的推力调控性能与上万小时仪器寿命进行技术攻关。
电喷微推力器的工作原理是电致锥射流与静电加速,工质(室温离子液体,Room Temperature Ionic Liquid)在高压电场的作用下,克服液体的表面张力使液体弯月面转化为泰勒锥,锥尖自由电荷的累积使场强迅速增强,最终导致电场力驱动液体脱离锥尖形成射流,射流在毛细不稳定性与瑞利极限作用下,在静电场中雾化为离子与带电液滴混合的电喷雾后经静电加速喷出,产生推力。电喷推力器发射过程受电压与流量调控,按照对工质流量的控制方式可以分为主动型和被动型两类。主动型电喷推力器须集成微流控系统以调控工质输运流量,一般由储罐、比例阀、流道与作为发射极的毛细管构成;被动型电喷推力器利用毛细力实现工质从储罐到发射极的输运过程,已报道的输运机制包括单管浸润、多孔材料浸润与表面浸润。对于主动型电喷推力器,其推力调控变量为电压与流量,电压/流量的不匹配会使发射进入单锥射流以外的发射模式,例如离轴发射、多股射流、脉冲射流[19]等。研究指出,工作在稳定单锥射流的电喷推力器相较于其他发射模式具有全频段噪声低,输出稳定[20]的优点,当流量和电压变化时,可用固有的物理模型评估输出推力大小[20]。因此,如何约束控制参量调节范围,使推力器始终工作在稳定单锥射流模式,是电喷推力器设计的重要问题。
本文基于我国空间引力波探测任务需求,开展微牛级电喷推力器稳定发射机制与调控特性的研究。设计搭建一套主动型电喷推力器真空试验系统,实现发射电压与工质流量的精密调控与发射电流的精密测量;分析稳定单锥射流的喷雾电流在不同参量下的时域与频域特性,提出一种以电流特征判定推力器发射模式的分析方法,并基于此方法测定单锥射流稳定域;利用该稳定域制定电喷推力器电压/流量调节范围,对单发射极推力器的分辨率、噪声、响应时间性能进行表征。
1 试验装置
1.1 电喷推力器发射原理试验系统构成
根据电喷推力器的工作原理与流量-电压变化的推力调控策略设计的推力器试验系统由三部分组成:推力器、工质储供系统以及测量系统,如图1所示。
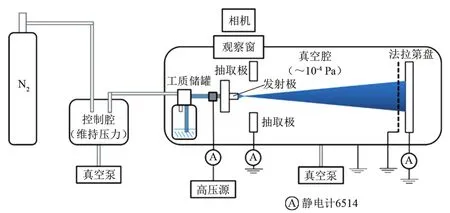
图1 试验装置示意图Fig.1 Schematic diagram of experimental device
推力器由支架,发射极(不锈钢毛细管)、抽取极以及高压电源构成,如图2所示。推力器支架采用3D打印制作,发射极为New Objective公司生产的不锈钢毛细管,长度为5 cm,内径为100 μm,外径为308 μm,毛细管尖端进行了尖锐化处理,最前端外径为165 μm。抽取极为中心开孔的不锈钢金属片,厚度为300 μm,开孔为6 mm,与发射极尖端相距2 mm。试验中,发射极与抽取极间的电势差通过高压电源Keithley 2290提供,范围为0~10 kV。

图2 电喷推力装置与稳定锥射流Fig.2 Photos of the colloid thruster and steady cone-jet mode in experiments
工质储供系统由一个真空腔(维持压力)与工质储罐构成,试验使用的工质为离子液体1-乙基-3-甲基咪唑双三氟甲磺酰亚胺盐(EMI-Im)。工质储罐通过一根长50 cm,内径500 μm的聚四氟乙烯PTFE软管连接至推力器发射极尾部。工质储罐内压力大小由气压控制腔决定(二者通过气管相连),该腔配有调节压力用的氮气瓶与真空泵。
测量系统由法拉第盘,静电计与采集卡构成,静电计Keithley 6514连接至发射极、抽取极与法拉第盘处(如图1所示),用来测量电流。法拉第盘放置于推力器单元之后,并根据试验需要调节其与抽取极间的距离(10~50 cm)。
试验中推力器单元与工质储罐共同放置于主真空腔内,该真空腔的工作压力设定为10-4Pa。
1.2 流阻标定试验
相较于被动型电喷推力器仅依靠电压调控,主动型电喷推力器当增加了流量调控后有更宽的推力调节范围。主动型电喷推力器的实际流量在nL/s量级,而现有的商用流量计检测极限在μL/s量级,无法满足检测需求,因此须对整个流量控制系统的流阻进行标定,利用压力与流阻评估流量大小。通过测量固定时间段内流出的工质质量计算系统流阻,试验方法为:设置工质储罐内外压力差Δp为某一固定压力值,将工质送至发射极尖端,发射极垂直放置,尖端朝下,下方放置培养皿以收集发射极尖端滴落的工质液滴,通过将一定时间内积累的工质液滴称重得到总质量M,再除以密度ρ与总时长t得到工质在该压力下的体积流量Q,取不同压力差Δp进行多组试验,得到一条压力差Δp与流量Q的曲线。再利用Poiseuille定律,将得到的曲线斜率(即流阻RH)与理论值进行对比。试验中,所有的流道都是截面为圆形的圆柱状流道,此类截面直径为d的圆柱形流道的流阻RH可用Poiseuille定律表达为:

流阻标定结果如图3所示,红色实线为试验测量值的拟合曲线,蓝色虚线为Poiseuille定律所描述的理论曲线。从图3可知,两条曲线斜率(流阻RH)的偏差为4.1%,其中试验曲线有截距,源于试验装置中发射极处液体与工质储罐内液面的高度差。

图3 流阻标定:试验曲线与理论曲线对比Fig.3 Flow resistance calibration:comparison between experimental curve and theoretical curve
2 电喷推力器稳定域内电压与流量调控特征
在2021年立项的科技部“引力波探测”重点专项中,对无拖曳控制中的推力器提出的指标为:推力范围为5~50 μN,推力分辨率优于0.1 μN。推力噪声在mHz频段小于0.1 μN/Hz0.5,响应时间小于50 ms。在实际使用中,调节电喷推力器的流量与电压即可调控推力的大小,但是前提条件为电喷推力器工作在稳定的单锥射流模式。试验中,在恒定的流量与电压下,测量并评估射束电流的时域频域特征以确定发射所处的射流模式,并且与光学成像结果进行比对验证,以确定是否工作在稳定的单锥射流模式。
电喷推力器的电压与流量通常都有开启阈值,达到该阈值后,无论是提升流量Q,或者电压V,都会度过一段稳定可控的单锥射流V-Q调控区间,但是最终会进入失稳状态。在不同的电压和流量条件下,失稳状态表现不同,如图4比较了0.9 kPa和1 kPa下的电流时域信号,当流量达到1 kPa时,电流表现为周期性失稳,即变为低频脉冲模式。出现该模式的主要原因是流量过大,与电压不匹配。在该状态下,时域上射流呈脉冲式发射。在图5的功率谱密度中,电流噪声相较于稳定单锥射流有明显提升。

图4 稳定单锥射流(红)与低频脉冲模式(蓝)的电流时域信号对比Fig.4 Comparison of current time-domain signal of steady cone-jet(red)and low-frequency pulsating mode(blue)

图5 稳定单锥射流(红)与低频脉冲模式(蓝)的电流噪声功率谱密度对比Fig.5 Comparison of current noise power spectrum density in steady cone-jet(red)and low-frequency pulsating mode(blue)
当电压持续增大至某一值时,出现多锥射流模式,试验中观测到的多锥射流模式的锥位置与锥形状不稳定,该模式的持续时间短,几秒后即消失,并在发射极管口处产生固体生成物,供液管道内产生气体空腔,结合这些试验现象,可认为是离子液体在发射极尖端发生电化学反应,这一现象可能与环境中的回流电子相关[21]。试验中观察到,出现多锥射流和电化学反应时的电压与流量无关,在不同的流量下电压均为较固定的值;射束电流信号相较于稳定锥射流信号明显表现出不稳定的时域特征,电流噪声在mHz频段明显提升。因此,将调控电压上限设置为增大电压的过程中发生多锥射流与电化学反应的最小电压值。
如图6中阴影部分所示,改变原理样机阴影范围内的流量与电压时,能稳定地形成单锥射流。该范围被称为稳定域[22],电压的上边界由电化学反应产生的电压所界定,下边界由脉冲模式形成的电压所界定,相较于不受流量影响的上边界固定电压,下边界同时受到流量与电压的影响。值得注意的是,流量主动控制下的电喷推力器一般工作在液滴模式,荷质比分布较为集中,电压的升高会使得离子的成分增加,影响荷质比的集中分布并影响推力效率。因此电喷推力器的推力调节以流量调节为主,电压调节通常会采用二极分压结构(发射-抽取-加速)形式,以保证电喷推力器在较低的恒定电势差下形成稳定的锥射流(发射-抽取),并同时具备电压调节下的推力调控能力(抽取-加速)[23]。

图6 电喷推力器稳定工作电压与流量范围Fig.6 Stable working voltage and flow rate range of the colloidal thruster in experiment
得到该稳定域后,可评估稳定域内调控参量能够覆盖的推力范围。评估之前,须表征电压、流量与电流的关系。假设电能完全转化为动能,根据动量定理,电喷推力器产生的推力可表示为[24]:

式中:q为电荷;V为电压;m为工质质量;t为时间;ρ为工质密度。
由式(2)可知,主动控制流量的电喷推力器系统中,只有电压与流量可以作为实时改变量,并且必须知道电流与电压及流量之间的关系。Mora等[25]在1994年的文献中,给出了这种主动控制流量操作下电流I与流量Q的关系:

Mora在试验中也得出了“电压对电流影响甚小,不起调控作用”的结论。在上述关系式中,K为工质的电导率,γ为工质的表面张力系数,ε为介电常数,f(ε)为不同介电常数下,无量纲电流与流量的比值。为了验证上述结论,控制电压或流量(气压)不变,改变另一项,并记录发射极,抽取极,法拉第盘上电流数据。将得到的I-Q数据进行曲线拟合,得到系数并与计算值进行对比。为了得到流量Q与电流I的关系,测量了一系列不同流量下的电流值,并进行了曲线拟合,得到如图7(a)所示结果,可以看出,流量Q与电流I成2次方关系,系数为5.84。将式(3)变形为:

代入文献中数值γ=0.0349 N/m;K=0.88 S/m;ε=10;f(ε)在6~8之间,计算得到系数为5.08~9.04,试验中得到的I-Q关系中的拟合系数5.84与文献给出的关系式中的系数相近。试验同样对定流量下不同电压的电流数据进行了采集,如图7(b)所示,与Mora的试验趋势相同。相较于流量Q与电流I的二次方关系,电流I没有因为电压V的大幅变化而明显改变,证明推力器工作在稳定的单锥射流模式。最后,由式(2)(3)计算得到图6中稳定域范围内推力器输出的推力范围为0.5~8.5 μN。

图7 推力器Q-I和I-V特性Fig.7 Thruster's Q-I and I-V characteristic curve
3 推力器性能表征
作为引力波探测应用的一种推力器,电喷推力器必须满足无拖曳控制提出的输出要求,诸如推力噪声,推力分辨率,响应时间等。本文利用测定的稳定域规定了单发射极电喷推力器电压/流量调节范围,对推力器的分辨率、噪声、响应时间等性能进行了表征。
试验中设置流量为3.1 nL/s,电压为2 kV,测量了14 h推力器稳定发射电流。在固定电压、流量条件下,推力器可长时间稳定发射,推力最大波动值小于0.1 μN。电流特征显示,测量期间推力器未进入单锥射流以外的发射模式,如图8(a)所示。在约1 μN的推力输出状态下,对时域推力数据作傅里叶变换计算得到的推力噪声水平在引力波探测敏感的mHz频段低于0.1 μN/Hz0.5,如图 8(b)所示,该推力噪声低于空间引力波探测任务的推力噪声需求。

图8 静态推力输出和推力噪声测试结果Fig.8 14 h static thrust output and thrust noise test results
通过电压台阶试验可测试输出推力的分辨率,台阶值为100 V,结果如图9所示。设置流量为0.5 nL/s,电压为2~2.4 kV,数据经过0.78 s滑动平均处理。电压变化时,单发射极推力分辨率约为0.04 μN,小于任务要求的0.1 μN。在该流量下调控推力器电压时,推力器仍然处于稳定锥射流模式,电压上调过程与下调过程的推力误差小于0.1 μN,证明在单锥射流模式下,单发射极推力器具有较高的推力调控精度,此分辨率低于空间引力波探测的分辨率需求。未来结合系统闭环反馈控制技术可进一步提升推力器精度与稳定性

图9 100 V电压台阶变化时的推力台阶变化Fig.9 Thrust step change under 100 V voltage step change
通过电压台阶试验可表征推力调节的响应时间,台阶值为300 V,结果如图10所示。设置流量为0.5 nL/s,电压为2~2.3 kV,调节电压时,得到输出电流从稳定值提升再次达到稳定的响应时间在10 ms以内,小于空间引力波探测任务要求的50 ms。更快的推力响应时间将拓宽无拖曳控制带宽,并为推力器闭环反馈控制技术与推力器阵列化数字调控技术的研制提供了基础。文献[26]中电压从关闭到开启,形成稳定单锥射流所消耗的时间约为100 μs,本文试验中通过电流信号得到的响应时间大于文献中通过高速成像得到的响应时间,但均小于50 ms的目标时间,证实稳定单锥射流对于电压调节有非常快速的动态反应性能。
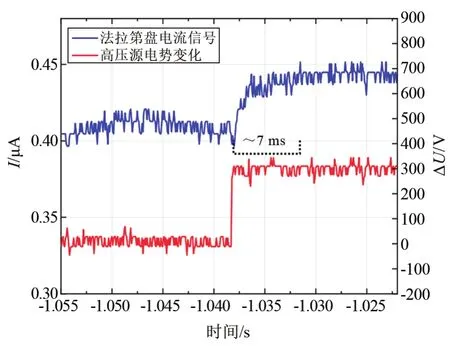
图10 300 V电压台阶变化时的电流响应时间测试结果Fig.10 Current response time under 300 V voltage step change
4 结论
本文介绍了电喷推力器的工作原理,梳理了国内外研究现状,研制了单发射极毛细管电喷微推力器原理样机,搭建了真空试验表征系统。通过分析稳定的单锥射流的喷雾电流时域与频域特征,提出了以电流特征判定推力器发射模式的方法,并对推力器原理样机稳定工作范围与电压流量调控特性进行了研究,对电喷推力器原理样机性能参数指标进行了表征,单发射极推力范围为0.5~8.5 μN,推力噪声小于0.1 μN/Hz0.5,推力台阶在100 V电压变化时小于0.1μN,推力随电压变化的响应时间小于10 ms。引力波探测要求的推力范围5~50 μN,若须实现50 μN推力范围的调节,多发射极阵列是一种增大推力范围的方案,但是发射极之间的串扰、不一致性以及更加复杂的工质储供系统是多发射极电喷推力器必须重点思考的几个问题,这些问题同时也影响推力器整体的性能,包括分辨率、噪声、寿命等。未来我们将重点研制阵列化的电喷推力器,并研究上述问题。

