变刚度复合材料螺旋弹簧的刚度预测模型及影响因素分析

李志虎，柯 俊，秦玉林，张 宁，张吉光，夏婉莹，严路平

变刚度复合材料螺旋弹簧的刚度预测模型及影响因素分析

李志虎，柯 俊，秦玉林，张 宁，张吉光，夏婉莹，严路平

（奇瑞汽车股份有限公司，安徽 芜湖 241009）

变刚度复合材料螺旋弹簧，不仅具有极好的轻量化效果，还能通过刚度的变化，提升整车的舒适性。目前变刚度复合材料螺旋弹簧的设计理论尚不完善，文章基于复合材料层合板理论，结合螺旋弹簧变刚度的原理，建立了变刚度复合材料螺旋弹簧刚度预测模型。根据变刚度复合材料螺旋弹簧的刚度预测模型，分析了各结构参数对刚度的影响灵敏度，其中结构参数的影响力大小分别为簧丝半径＞中径＞有效圈数＞芯轴半径。文章推导的刚度预测模型和影响灵敏度分析，可快速指导变刚度复合材料螺旋弹簧的结构设计。

变刚度；复合材料；螺旋弹簧；刚度预测模型；结构设计

“节能减排，发展低碳经济”已在全球范围内形成高度的共识。汽车轻量化可有效降低能源消耗，减少尾气排放，汽车每减重100 kg，传统燃油汽车百公里油耗可降低0.2 L～0.8 L[1]，二氧化碳排放可减少约5 g/km。连续纤维增强复合材料具有比强度、比模量高的特点，其在汽车轻量化方面具有巨大的潜力。目前，连续纤维增强复合材料已经在沃尔沃板簧、奔驰SLS传动轴、宝马I3车身骨架、蔚来ES8地板、前途K50全车外覆盖件等车型零件上使用。

复合材料螺旋弹簧，由于其质量远小于传统的钢制弹簧，轻量化效果超过30%。目前复合材料螺旋弹簧已在奥迪A6前悬架进行量产化应用，另外，在一汽大众、广汽等主机厂，也有复合材料螺旋弹簧的应用开发研究。为推进复合材料螺旋弹簧在汽车上的应用，近几年国内也开展了大量的研究。北京理工大学的陈潇凯开展了纤维增强复合材料螺旋弹簧的刚度预测，对复合材料螺旋弹簧的刚度设计进行了理论推导和计算机辅助工程软件（Computer Aided Engineering, CAE）分析验证，其理论推导和CAE分析结果有较好的一致性[2]。熊志远、葛勇、答建成等人则借鉴传统的金属螺旋弹簧刚度公式，结合复合材料的特性，推导出复合材料螺旋弹簧的刚度计算模型[3-5]。以上研究还主要是停留在理论阶段，并没有进行样件试制，并根据实际样件的刚度结果，对理论推导模型进行修订。

目前复合材料螺旋弹簧的研究，仅仅还局限于定刚度复合材料螺旋弹簧，相对于金属弹簧，主要作用是轻量化。本文介绍的一种变刚度的圆柱形复合材料螺旋弹簧，相对于传统的金属螺旋弹簧，该复合材料螺旋弹簧不仅可达到40%以上的减重，还能通过结构的设计，实现螺旋弹簧在使用过程中，根据运动状态进行刚度调节，从而更有效吸收高冲击能量，提高整车行驶舒服性。

本文重点提出了一种新型变刚度复合材料螺旋弹簧的刚度预测模型，并对其影响的各种因素进行了探讨，为变刚度复合材料螺旋弹簧的设计提供理论依据，促进复合材料螺旋弹簧在汽车上的应用。

1 变刚度的原理

螺旋弹簧一般是通过改变其在工作状态下的有效圈数来实现刚度的改变，而改变有效圈数的方法主要有两种：一种是螺旋弹簧有效圈之间的自接触，如螺旋弹簧簧圈之间的压并；另一种是螺旋弹簧有效圈与外界发生贴合[6]。复合材料螺旋弹簧，由于材料的特性，一般不允许簧圈之间发生压并，所以是通过螺旋弹簧有效圈与螺旋弹簧底座之间发生贴合而改变的。

本文研究的复合材料螺旋弹簧为腰鼓形结构（见图1），其中A、C段呈对称形，中径和线径逐渐减小。B段中径和线径固定。

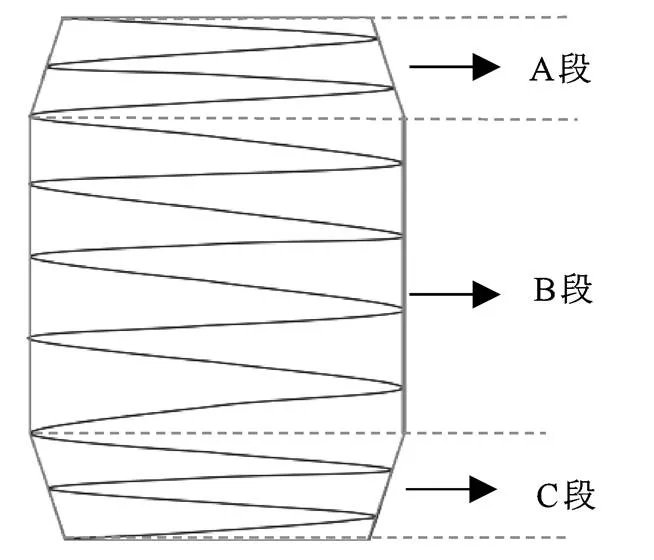
图1 腰鼓形复合材料螺旋弹簧结构

根据螺旋弹簧串联定理，当有个刚度分别为1，2，…，k的螺旋弹簧串联在一起时，螺旋弹簧的总刚度值为[7]

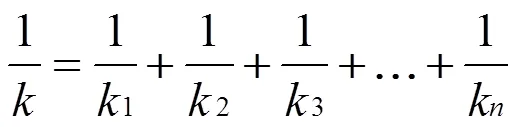
当研究形状复杂的螺旋弹簧刚度特性时，采用离散化思想进行分析，将螺旋弹簧离散化为小段，各段之间相当于串联连接，每小段复合材料螺旋弹簧的刚度近似看为定值。则螺旋弹簧发生压并前即初始状态的总刚度可以由串联定理式（1）表示。

图1形状的螺旋弹簧，其总刚度值（）为

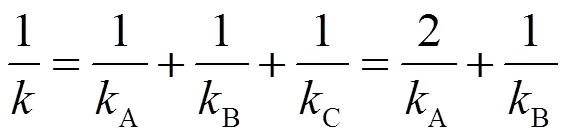
在汽车行驶过程中，随着受力的增大，A、C部分会逐渐并圈并与弹簧底座贴合。随着贴合程度的增大，该部分弹簧刚度逐渐变大。当A、C部分完全贴合到底座上时（此时，KA=KC，均为无穷大），弹簧总刚度K=KB。螺旋弹簧在整个运动阶段，其刚度变化示意图如图2所示。

2 刚度预测模型

图3为变刚度复合材料螺旋弹簧有效圈数的示意简图，它由两端线径及中径逐渐减小的过渡圈与等中径、等线径的中间圈组合而成，其中1为有效圈最小丝径，2为最大丝径，1为最小中径，2为最大中径。

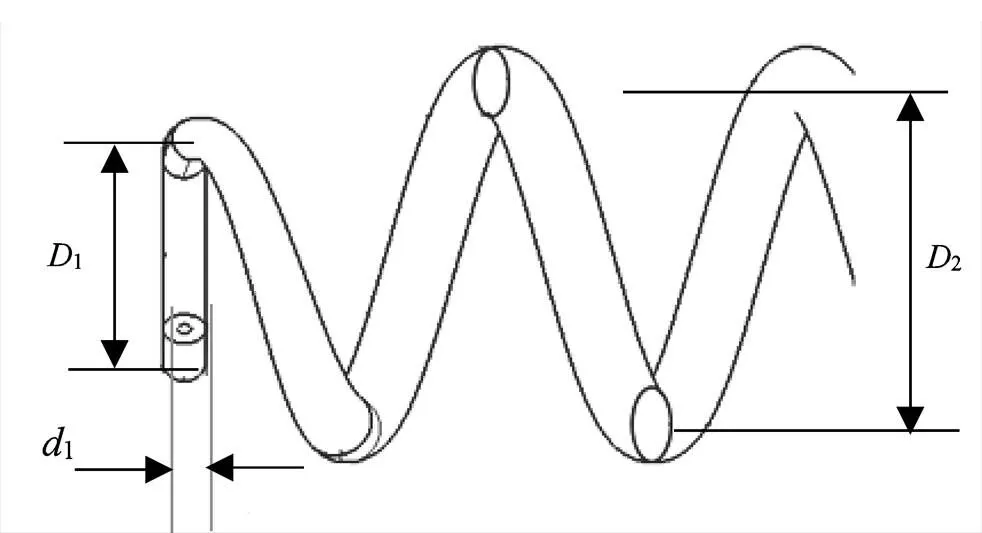
图3 变刚度复合材料螺旋弹簧结构示意简图

复合材料螺旋弹簧的设计选用两层材料结构。其横截面分为两层，中间层为聚氨酯芯轴，外层则采用的是玻璃纤维或碳纤维增强复合材料。

根据金属螺旋弹簧的刚度公式以及复合材料的分层积分理论，可推导出定刚度复合材料螺旋弹簧的刚度计算表达式[8-9]为

式中，为螺旋弹簧受到的垂直向下压力；为弹簧在压力下的垂直变形量；为有效圈数；为弹簧中径。22()为螺旋弹簧刚度系数，其与螺旋弹簧的线径有直接的关系。根据文献[9]可知，J2()与螺旋弹簧线径（含芯轴部分的线径i）之间的关系为

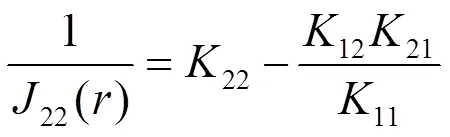
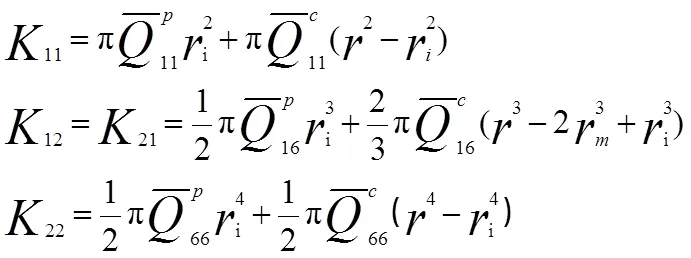
式中，K为根据复合材料分层积分理论下复合材料螺旋弹簧的中截面刚度系数；Q是纤维增强复合材料的变换刚度系数；Q是芯材材料的变换刚度系数，其表达式为

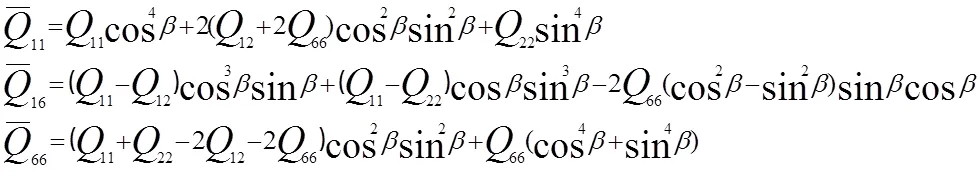
式中，是纤维增强复合材料螺旋材料中纤维材料的铺层角度。11，12，22，66与复合材料的材料参数相关，其关系式为

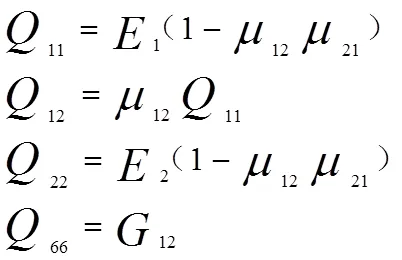
螺旋弹簧的两端部分（即图1中的A和C），由于弹簧丝径及中径都是变化的，可以采用无限切割的方法，将整段的变中径部分分为若干段，每一段的圈数为（足够小）圈，则总共分成的段数为/段。设该部分的中径变化为1→2，弹簧丝径变化为1→2。最终的刚度A可用式（8）表示。

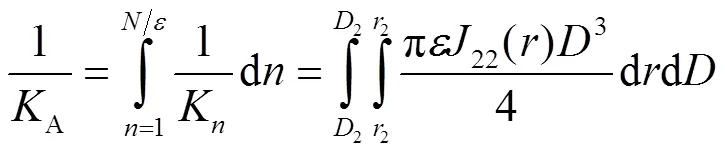
最终螺旋弹簧的刚度与图2一致，在两端并圈前的刚度（1）为

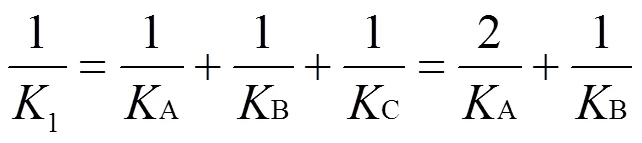
在两端并圈后，弹簧的刚度（2）：2=B。

3 刚度影响分析

由以上理论预测模型可以看出，变刚度复合材料螺旋弹簧的刚度影响因素主要有两方面：复合材料的材料参数、螺旋弹簧的结构参数。

影响复合材料螺旋弹簧刚度的材料参数主要有1（复合材料纵向弹性模量）；2（复合材料横向弹性模量）；12（复合材料层间剪切强度）；12（复合材料横向泊松比）；21（复合材料纵向泊松比）；p（芯材弹性模量）；P（芯材层间剪切模量）；p（芯材泊松比）；（铺层角度）等。

影响复合材料螺旋弹簧刚度的结构参数主要有（有效圈数），（中径），（簧丝半径），i（芯轴半径）等。

由于材料的选用在产品设计前期已经确定，在产品开发过程中，主要通过产品结构参数的调整，确定最终产品的刚度，故本文主要探讨各结构参数对螺旋弹簧刚度的影响。

本文初步选定复合材料螺旋弹簧结构参数如表1所示。

表1 变刚度复合材料螺旋弹簧结构参数

表1中A、A、A只影响两端的刚度，B、B、B、i则对两端和中间段的刚度都有影响。

图4为有效圈数与刚度值的关系图，从图4(a)中可以看出，刚度A和有效圈数A互成负相关关系，随着等中径部分有效圈数A的增大，A逐渐减小。

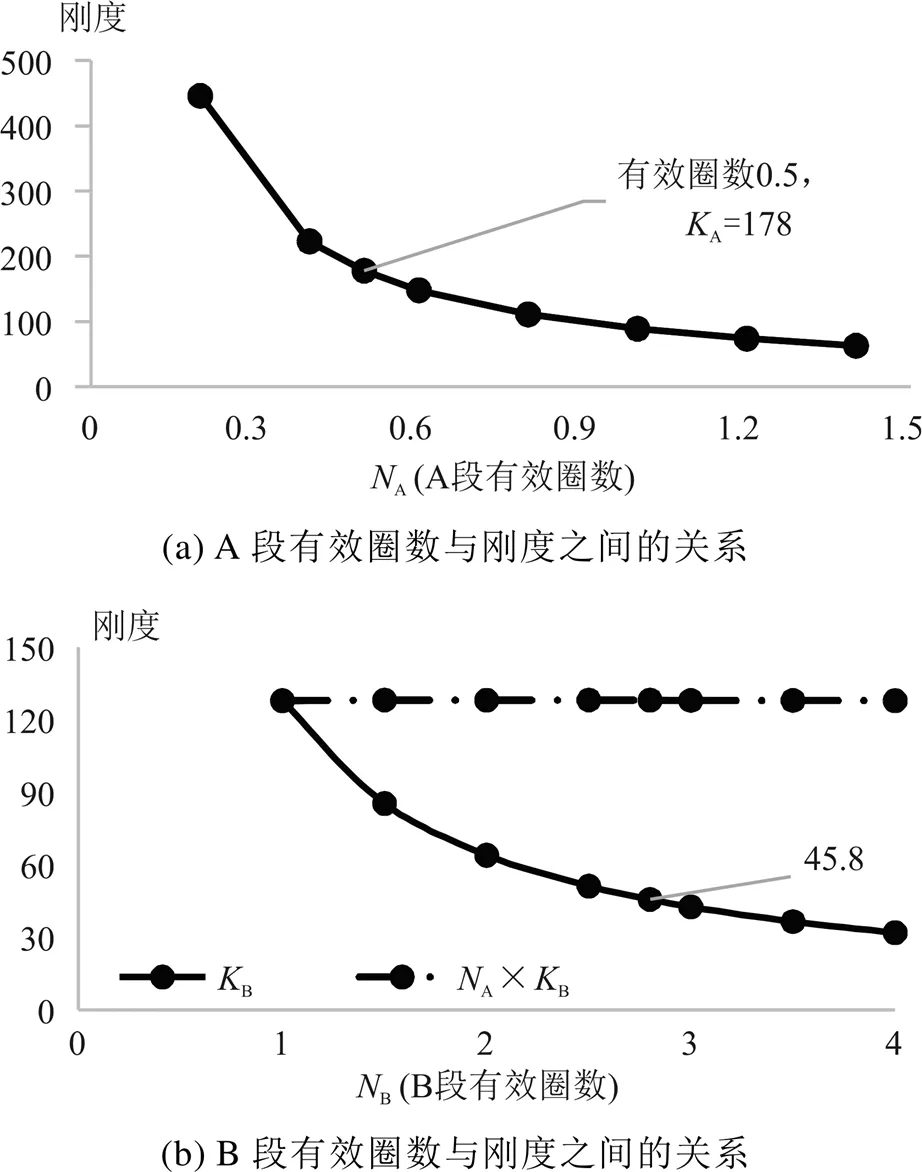
图4 有效圈数与刚度值的关系

从图4(b)中可看出，刚度B与B的乘积为定值，即B与B互为反比例关系。

图5是中径与刚度值的关系，从图5中可以看出，复合材料螺旋弹簧B段的中径与弹簧刚度成负相关的关系，随着中径B的增大，B与A逐渐减小。复合材料螺旋弹簧A段的最小中径与B关系不大，其主要影响A段刚度，呈负相关的关系，随着中径A的增大，A逐渐减小。

图5 中径与刚度值的关系

在B段，复合材料螺旋弹簧的中径均匀，刚度B和中径B的三次方的乘积为定值，即刚度B和中径B的三次方互成反比例关系。

图6是弹簧簧丝线径B与弹簧各段刚度值的关系。从图中可以看出，A段、B段的刚度和弹簧簧丝线径B正相关的关系，随着弹簧簧丝线径B的增大，A、B逐渐增大。

图6 B段线径（RB）与刚度值的关系

图7是B段簧丝的四次方与弹簧刚度的关系，从图中可以看出，B段弹簧的刚度B与该段弹簧线径的四次方（B4）基本呈正比例关系。

图7 B段刚度与丝径（RB）之间的关系

图8是弹簧簧丝线径A与弹簧各段刚度值的关系。从图中可以看出，A段的刚度和弹簧簧丝线径A正相关的关系，随着弹簧簧丝线径A的增大，A逐渐增大，基本为不严格的正比例关系。B段的刚度和弹簧簧丝线径A关系不大，基本为定值。

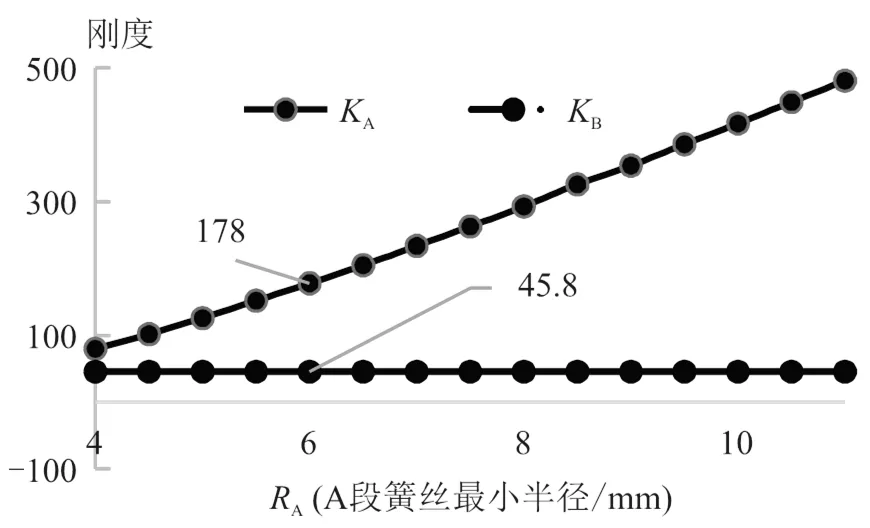
图8 A段刚度与丝径（RA）之间的关系

图9是芯轴半径i和弹簧刚度的关系图，由图中可以看出，随着芯轴半径的增大，无论是弹簧A段的刚度，还是B段的刚度，都呈先增加后降低的趋势。但总体来说，由于芯轴本身直径较小，其对螺旋弹簧的刚度影响较小。

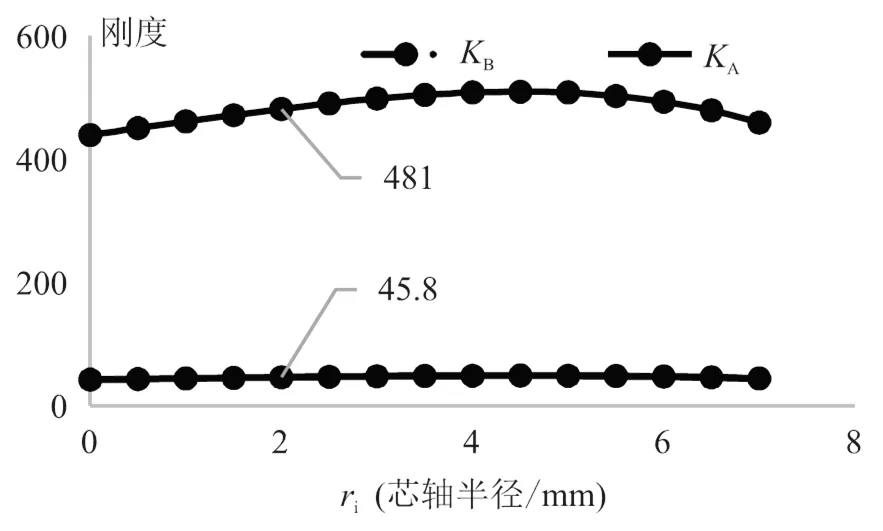
图9 芯轴半径ri和弹簧刚度的关系图

通过以上弹簧结构参数（有效圈数），（中径），（簧丝半径），i（芯轴半径）对弹簧各段的刚度影响分析可以看出，影响力分别为：＞＞＞i。在复合材料螺旋弹簧设计过程中，可以根据每个参数的影响力来调节整体的刚度值，若刚度的调节幅度较大，则可选择调节影响力大的结构参数，以便达到最大的调节效率。

4 结束语

本文介绍了一种复合材料螺旋弹簧，相对于传统的金属螺旋弹簧，具有轻量化、刚度可变的优点。基于复合材料细观力学方法，对单层复合材料的弹性常数进行理论计算，又根据经典层合板理论和传统螺旋弹簧刚度计算公式，研究推导了一种新型变刚度复合材料螺旋弹簧的刚度预测模型，并基于该模型，进一步分析了影响刚度的结构参数及其影响程度。

影响变刚度复合材料螺旋弹簧的材料参数主要有弹性模量、层间剪切强度、泊松比、铺层角度等，结构参数主要有有效圈数、中径、簧丝半径、芯轴半径等。其中结构参数的影响力大小分别为簧丝半径＞中径＞有效圈数＞芯轴半径。

[1] 李军,路洪洲,易红亮,等.乘用车轻量化及微合金化钢板的应用[M].北京:北京理工大学出版社,2015.

[2] 陈潇凯,李超.纤维增强复合材料螺旋弹簧刚度预测模型[J].北京理工大学学报,2020,40(7):725-730.

[3] 熊志远,宋瑞祥,赵娜,等.圆柱螺旋弹簧轻量化设计探讨[J].机械设计与制造,2022(3):176-180,184.

[4] 葛勇,赵光艺.碳纤维复合材料圆柱螺旋弹簧力学性能分析[J].装备制造技术,2020(9):209-212.

[5] 答建成.碳纤维增强复合材料弹簧的制备及模拟研究[D].上海:上海工程技术大学,2016.

[6] 肖光育,周磊,金敏桢.腰鼓型变刚度螺旋弹簧的设计[J].时代汽车,2019(12):73-75.

[7] 方子帆,郑小伟,何孔德,等.多段式组合变刚度悬架螺旋弹簧设计与研究[J].机械设计与研究,2018,34 (6):75-79.

[8] 刘宇宸,花军,宁礼佳.碳/玻璃纤维混编复合材料压簧制作方法及实验研究[J].复合材料科学与工程, 2021(2):43-48.

[9] 杨永宝,金达锋,高希.CFRP圆柱螺旋弹簧静刚度预测理论及仿真[J].汽车技术,2013(7):21-25.

A Stiffness Prediction Model and Impact Analysis for Variable Stiffness Composite Material Helical Spring

LI Zhihu, KE Jun, QIN Yulin, ZHANG Ning, ZHANG Jiguang, XIA Wanying, YAN Luping

( Chery Automobile Company Limited, Wuhu 241009, China )

Variable stiffness composite helical spring, not only has excellent lightweight effect, but also through the change of stiffness, improves the comfort of the vehicle. At present, the design theory of variable stiffness composite helical spring is not perfect, this paper based on the theory of composite laminates, combined with the principle of variable stiffness of helical spring, a stiffness prediction model of variable stiffness composite helical spring is established. Based on the stiffness prediction model of the variable stiffness composite helical spring, the sensitivity of the influence of the structural parameters on the stiffness is analyzed, among them, the influence of structure parameters on the radius of the spring wire > the middle diameter > the number of effective rings > the radius of the mandrel. The stiffness prediction model and influence sensitivity analysis derived in this paper can quickly guide the structural design of variable stiffness composite helical springs.

Variable stiffness; Composite material; Helical spring; Stiffness prediction model;Structural design

TB33

A

1671-7988(2022)24-124-05

TB33

A

1671-7988(2022)24-124-05

10.16638/j.cnki.1671-7988.2022.024.023

李志虎（1979—），男，硕士，高级工程师，研究方向为新材料新技术相关的汽车产品开发。

安徽省重点研究与开发计划项目（202104a05020073）。