基于IPSO-LSTM的高校贫困生精准资助方法

杜兴丽 刘 玲 袁 平

（1.西南科技大学计算机科学与技术学院 四川绵阳 621010；2.西南科技大学教育信息化推进办公室 四川绵阳 621010）

大数据技术在高校信息化建设中的运用越来越受重视，在中共中央、国务院印发的《中国教育现代化2035》中指出要推进智能化校园建设，推进管理精准化和决策科学化［1］。高校日常运行产生的大量数据能为学校管理精准化提供数据支撑，建立有效的教育大数据分析模型，能对学校招生计划、学生资助、安全防控等决策提供支持。

教育数据挖掘囊括了学生的学习表现、职业选择预测、生活情况等多方面。研究者的关注点包括学生辍学预测［2］、学生成绩预测［3-4］以及学校对学生成绩的影响［5］等。文献［6］使用集成模型选择方法进行教育数据挖掘；文献［7］采用无监督学习方法对MOOC课程进行优先级建模分析；文献［8］提出基于XGBOOST模型的聚类中心模型来预测学生的职业选择。这些研究关注学生学业生活，对学生在校的消费数据挖掘不够充分。国家在教育上投入资金是期望帮助学生高质量完成学业，现有问题是如何让教育资助发放到最需要帮助的学生手中。

传统高校经济困难学生资助评审依靠学生的主观陈述，所述内容不能客观反映学生阶段性的经济情况。利用学生在校消费数据构建经济困难学生分类模型是解决精准资助问题的办法之一。文献［9］利用聚类算法快速判定贫困生类别。文献［10］利用CHAID算法找出最佳分组变量和分组点，设计判别贫困生的模型。文献［11］使用学生“一卡通”消费记录，构建高校贫困生精准资助的神经网络模型。文献［12］采用正负序列模式挖掘算法对学生的消费数据进行分析。文献［13］提出一种深度学习算法来处理学生数据，挖掘高校学生行为产生的海量数据的价值。文献［14］研究发现贫困生与其他学生的消费行为存在明显差异，贫困生资助对于学生的消费水平会产生短期效应，但无长期效应。文献［15］将“一卡通”数据和学生网贷数据相结合，为高校管理者提供帮助经济困难学生的新思路。文献［16］利用校园卡的消费数据结合自适应优化算法和逻辑回归算法构建贫困生识别模型。文献［17］通过学生的海量校园数据构建学生自画像，描述学生特征。文献［18］基于校园一卡通大数据对学生消费行为进行分析，使用聚类算法为高校精准资助工作提供支持，并构建学生共现网络，发现孤独者，为心理资助提供参考。

上述研究中，研究者已开始探索如何将神经网络算法应用到贫困生的分类中，但是在运用神经网络解决此类问题时，对于神经网络存在的参数确定困难问题，没有给出解决办法。本文以学生在校期间的消费数据、学生出入校园场所记录数据和学生基本信息数据，结合神经网络算法，构建学生经济困难分类模型。结合学生消费数据的时序特点，使用长短期记忆神经网络（Long short-term memory，LSTM）构建分类模型，针对LSTM参数手动调整困难的问题，使用改进的粒子群优化算法（Improved particle swarm optimization，IPSO）对LSTM的学习率和隐藏层节点数进行优化，提高模型的分类准确率［19］。

1 算法理论

1.1 长短期记忆神经网络

LSTM能够很好处理时序数据，并在一定程度上解决循环神经网络梯度消失或梯度爆炸的问题。LSTM引入了输入门、输出门和遗忘门［20］来控制信息的传递，该算法核心在于记忆单元的设计，每个单元的计算公式如（1）式至（7）式所示，ft，it和ot分别表示遗忘门、输入门和输出门；ht为隐藏状态；xt为输入的样本；bf，bi，bo和bc为参数；Ct和C～t分别表示记忆细胞和候选记忆细胞。在LSTM模型中，需要手动调整学习率、隐藏层节点数，直到达到良好的分类效果。本文针对这一问题，引入粒子群优化算法，对学习率和隐藏层节点数进行参数寻优。

1.2 粒子群优化算法及其改进

粒子群优化算法（Particle swarm optimization，PSO）是群智能优化算法的重要组成部分，可用于深度神经网络中的权值优化［21］。该算法通过模拟鸟的不断飞行达到搜索的效果。算法输入的每一个个体根据自身的搜寻能力，在n维空间寻找个体的最优解，然后通过全局跟踪对比，寻找整个群体的全局最优解。算法通过k次迭代，不断调整粒子的自身位置和飞行速度，最终收敛到全局最优解。n维空间中m个粒子，粒子的位置可表示为Xi＝［Xi1，Xi2，…Xin］，i取值为1到m，在整个寻优过程中，每个粒子的更新速度可表示为Vi＝［Vi1，Vi2，…Vin］，每个粒子搜寻到的最优位置可表示为pbesti＝［pi1，pi2，…pin］，在整个粒子群中，群体的最优位置表示为gbest＝［g1，g2，…gn］，搜索过程中，需要限定位置范围［Xmin，Xmax］，限定速度范围［Vmin，Vmax］。k次搜索迭代过程中，粒子的更新变化可表示为：

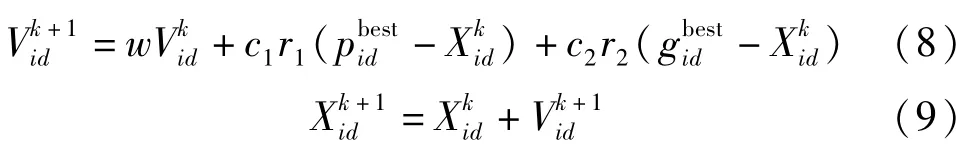
式中：d＝1，2，…n；i＝1，2，…m；w表示惯性权重，若没有惯性权重会因无法知道初始状态而造成寻优困难；c1和c2表示学习因子，能够调节学习的步长，c1为0容易陷入局部最优解而无法跳出，c2为0会导致收敛缓慢，c1和c2均不为0算法更容易保持收敛速度和搜索效果的均衡性；r1和r2是两个随机数，取值范围为［0，1］，用于增加搜索的随机性。

PSO算法参数较少且收敛速度较快，标准的粒子群优化算法易陷入局部最优，且需要重视初始粒子位置，w惯性权重是描述粒子历史状态的参数，会在每次搜索中影响当前的搜索效果，是可优化PSO性能的重要参数［22］。本文通过改进惯性权重w，解决算法易陷入局部最优的问题，w能够较好平衡搜索速度和搜索进度，提升算法性能。因为速度过大，粒子容易越过最优解，速度过小容易陷入局部最优解。在实际搜索过程中，空间较大时，前期需要较高的全局搜索能力，后期需要较高的局部搜索能力，因此，w可设置为动态更新的函数，本文将w修改为：

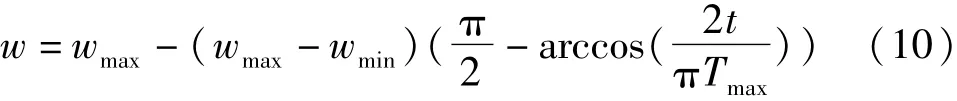
式中：wmax是w的最大值；wmin是w的最小值；Tmax是最大迭代次数；t为当前迭代次数。

为避免粒子搜寻陷入局部最优解，加入自适应变异操作，计算公式如式（11）所示。

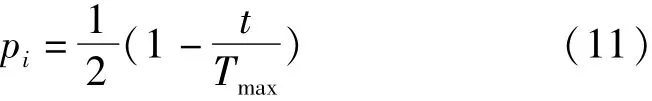
式中：Tmax是最大迭代次数；t为当前迭代次数；pi为自适应变异几率。

2 数据来源与数据处理

2.1 数据来源

本文使用某高校提供的2020年10月至2021年7月一学年的本专科学生校园消费数据，涉及学生31 645名。高校一卡通数据库有本专科生、研究生、教职工、外来人员和临时员工的所有消费记录，但在经济情况的判断中，由于研究生、教职工、外来人员和临时员工的消费记录分散，无法进行系统的分析，因此将这一类数据剔除。学生校园一卡通的消费数据具有时间限制，所取数据的高校位于四川省，根据学校提供的供餐时段以及在校学生日常作息情况，以上午10：00和下午15：00为界线区分早餐、午餐和晚餐，抽取学生消费的时序特点并且计算在校学生的消费次数。

数据集包括学生的基本信息和消费信息，部分数据字段如表1和表2所示，本文实验重点关注消费数据。学生的基本信息包含学号（xh）、姓名（xm）、性别（xb）、身份证件号（sfzjh）、学院名称（xymc）、班级（bj）等，学生在校内的消费情况部分重要字段为消费金额（jyje）、消费时间（jysj）、消费地点（ZHMZ）等，消费地点囊括了学生食堂、超市、水房等场所。

表1 高校学生部分基本信息Table 1 Some Basic information of college students

表2 消费记录（部分）Table 2 Consumption Record（partial）

本文从学生的基本信息和消费记录中提取特征，作为IPSO-LSTM模型的输入。学生的基本信息主要抽取学生的性别、年级、生源地以及专业，重点抽取消费记录中所隐含的特征。学生在校的消费情况能反映出学生经济状况，根据消费记录，抽取学生的基本消费特征，主要特征有消费总次数、消费总金额、每次消费平均值、每月消费平均值、周消费次数以及月消费次数等，消费的时间段作为数据重要的区分特征。

2.2 数据定义

根据高校学生的消费规律，可计算在一段时间内一所高校学生的消费平均水平，以此可确定该校整体经济情况，并且能够确定一段时间内该生经济情况。为划分出在校学生的经济情况，本文给出了相关数据定义及其计算方法。

定义1校内学生月消费平均水平：学生群体的整体消费情况可用一段时间内该群体的平均消费水平展示，记作M_average，计算公式如式（12）所示：

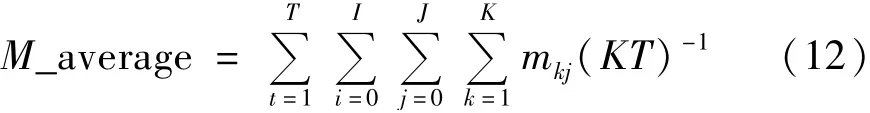
公式含义为k位学生i天t月j次在校内消费的总额与在校消费学生总数K和该时段总月数T的商；mkj表示第k位学生第j次的消费金额；J表示消费的总次数；I表示每月消费的总天数；K，J，I和T均为正整数。

定义2经济困难水平线：处理好异常数据后所有能够参与经济资助评定的K位学生中，若消费水平低于经济困难水平线，则该同学在该时段出现经济困难的概率越大，记作LOPC，计算公式如式（13）所示：

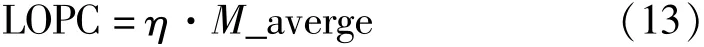
式中：η为可调整系数，取值大于0小于1，可根据高校的资助名额进行调整。

定义3经济困难判定应满足以下条件：（1）学生月消费总额小于LOPC；（2）学生月消费次数大于n；（3）学生连续m月在校消费。n为设定的每月消费次数，m为设定的在校消费月数。当3个条件均满足时，认为该同学经济困难，反之则不困难。

在本文的实验中，η的系数取值设置为0.3；n的取值设置为30；m的取值设置为3。

3 基于IPSO-LSTM的分类模型

本文使用改进后的粒子群优化算法（IPSO）对LSTM的学习率和隐藏层节点数进行寻优，将参数寻优结果用于LSTM模型训练，并结合学生在校消费数据构建分类模型。

基于IPSO-LSTM的贫困生分类模型如图1所示，基于IPSO-LSTM的分类模型伪代码如表3所示。

表3 IPSO-LSTM分类模型伪代码Table 3 IPSO-LSTM classification model pseudocode

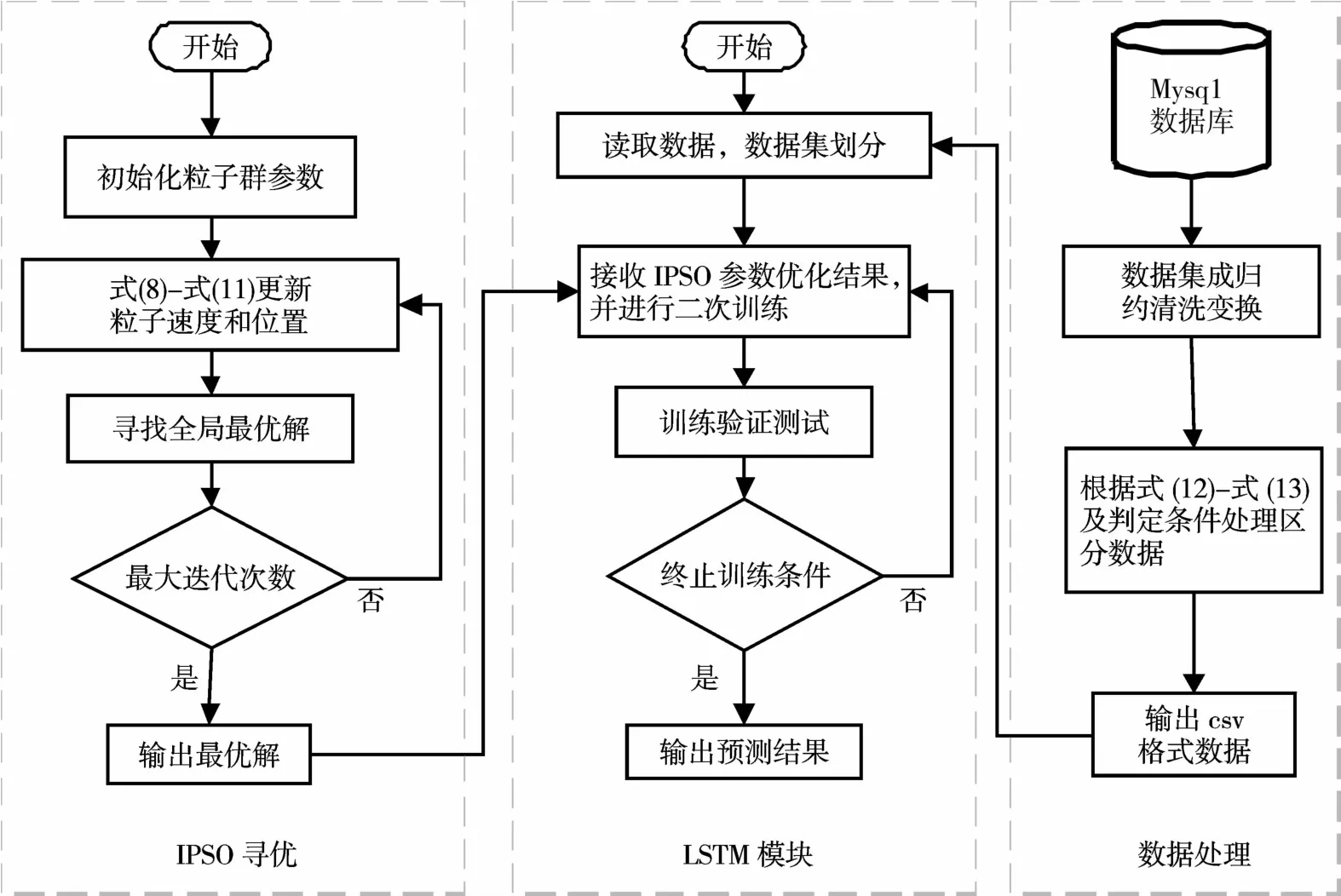
图1 IPSO-LSTM算法模型Fig.1 IPSO-LSTM algorithm model

4 实验分析

4.1 实验评价指标

本文的研究目的是利用LSTM网络构建贫困生分类模型，完成贫困生的类别划分任务，解决传统贫困生识别方法受人工经验影响较大的问题。因此本文选择常用于分类问题的评价指标来进行模型的性能评估，实验评价指标包括准确率（Accuracy）、精确率（Precision）、召回率（Recall）和F1-score。各评价指标的数学表达式如下所示：

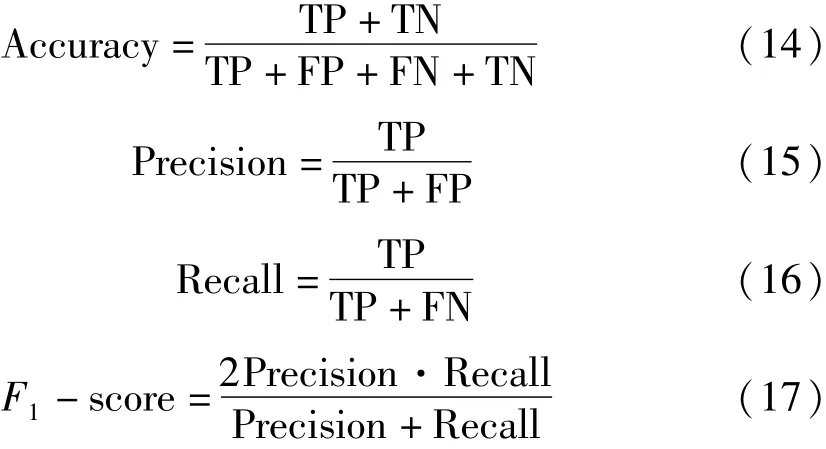
式中：TP表示分类正确的正例；FP表示分类错误的正例；TN表示分类正确的反例；FN表示分类错误的反例。

4.2 实验验证

4.2.1 基于IPSO的网络参数优化

本文模型利用IPSO的自适应搜索特点确定LSTM网络的相关结构参数，解决LSTM网络参数确定困难的问题。

设置粒子个数为3，迭代次数为10；wmax为0.8，wmin为0.2。在寻优过程中，通过式（8）到式（11）更新粒子速度和位置，IPSO-LSTM寻优收敛情况如图2所示。其中：图2（a）为算法寻优适应度曲线，以错误率函数进行评估，收敛在0.203 57；图2（b）为LSTM学习率寻优结果为0.000 26；图2（c）为LSTM第一个隐藏层节点数，取值结果为149；图2（d）为LSTM第二个隐藏层节点数，取值为175。

图2 改进粒子群优化算法寻优结果Fig.2 Optimization results of improved particle swarm optimization algorithm

4.2.2 基于IPSO-LSTM的贫困生分类

利用IPSO的自适应优化获取LSTM的网络结构参数后，利用该参数二次训练模型。

设置迭代次数为1 000、移动步长为16，数据集总样本数为10 008条，采用8∶2随机划分训练集与测试集。贫困生分类模型训练过程中整个模型准确率和损失率的变化如图3所示，其中：图3（a）为IPSOLSTM算法损失曲线；图3（b）为IPSO-LSTM分类准确率曲线。在训练至800次左右，算法收敛，最终分类预测准确率收敛在98.3%。

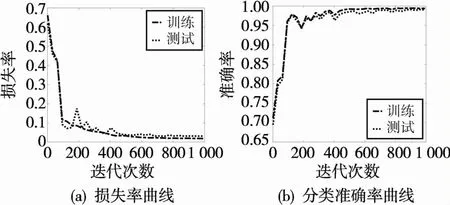
图3 IPSO-LSTM损失率和准确率Fig.3 IPSO-LSTM loss and accuracy

同时，为提高本文所提方法的说服力，本文将所提方法与LSTM和PSO-LSTM算法进行对比。为防止偶然实验对结果的影响，本文利用十折交叉验证理念设计对比实验，实验结果如表4所示。实验表明本文所提方法表现良好，略优于对照算法。

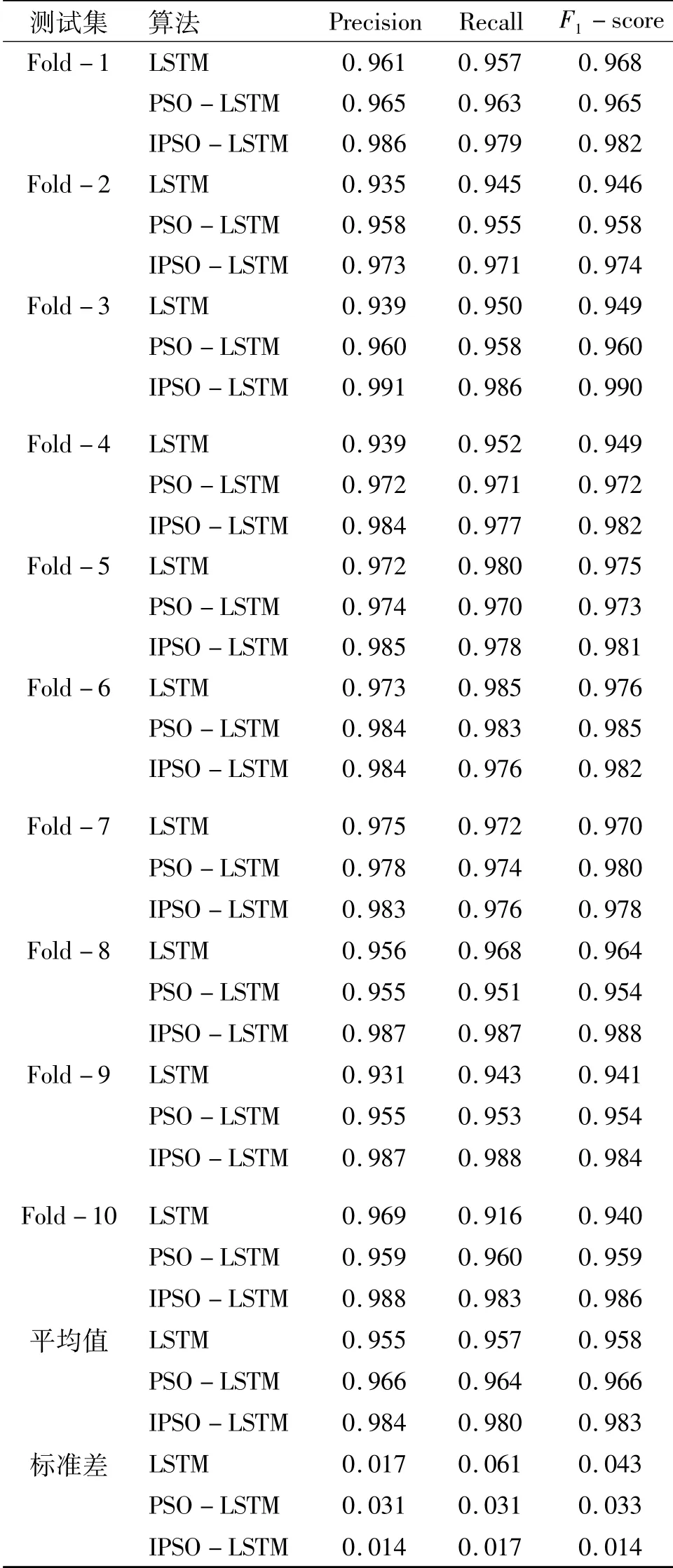
表4 十折交叉验证数据Table 4 Ten fold cross validation data

通过实验可以发现，改进后的粒子群优化算法进行隐藏层节点数和学习率的参数寻优后，随着迭代次数的增加，IPSO-LSTM的分类结果越准确。IPSO参数调整后，算法的收敛速度和寻优精度表现良好，验证实验表明，IPSO-LSTM的稳定性和准确率较好。

5 结论

本文抽取学生的基本信息和消费信息，构建基于IPSO-LSTM的经济困难学生分类模型，用于困难学生的识别，对IPSO-LSTM算法进行验证测试，实验结果表明IPSO-LSTM模型在经济困难学生识别问题上的整体表现效果较好，收敛速度较优，准确率较好。本文的研究工作能够为高校精准帮扶贫困学生提供理论与实践参考，研究方法能为教育数据挖掘领域同类型研究提供参考。