宽高比13.57的宽幅半封闭箱梁的涡激振动特性

段青松

（西南科技大学土木工程与建筑学院 四川绵阳 621010）

随着我国桥梁建造技术水平的提高，桥梁向更纤细、更轻柔方向发展。设计者对典型的流线型钢箱梁进一步创新，提出半封闭箱梁断面形式，并逐渐在大跨桥梁中应用［1］。表1列出了部分大跨度半封闭箱梁结构的部分参数。与流线型钢箱梁断面相比，半封闭箱梁去除了部分底板，以沿桥梁纵向分布的横隔板代替，半开口位置处会形成较大的旋涡，影响其绕流结构进而弱化主梁的涡激振动性能［2-4］，并成为该类断面形式主梁面临的共性问题。近年来西堠门大桥、虎门大桥、鹦鹉洲大桥、日本东京湾跨海大桥等发生的涡激振动事件影响较大［5-6］，大跨桥梁的涡激振动性能引起诸多学者的关注。

表1 部分半封闭箱梁桥梁列表Table 1 Some Bridges of semi-closed girder

孟晓亮等［7］对比了封闭和半封闭钢箱梁的涡振特性，认为风嘴角度可以改善桥梁的涡振性能，原因是风嘴角度变化引起了桥梁断面外部绕流的变化，当气流流经风嘴角度较小的封闭箱梁断面时，不容易形成频率低、能量高的漩涡，而对于半封闭箱梁断面，外部绕流流态复杂，风嘴角度对外部绕流的改变程度相对较小。针对窄幅半开口主梁断面的涡振性能，朱乐东等［8］提出在主梁底板外缘安装多孔扰流板以抑制主梁涡振，迎风侧的多孔扰流板对半封闭窄箱梁能起到很好的减振或消振作用，而背风侧多孔扰流板减振效果不如迎风侧多孔扰流板，甚至可能会起到放大竖向涡激振动的作用。方根深等［9］通过风洞模型试验和数值模拟对半封闭箱梁的涡振性能进行了测试，认为检修道栏杆是引起主梁涡振的主要原因，并提出了对应的抑制措施，其中水平翼板和抑流板都能有效控制竖弯涡振。高云峰等［10］对半封闭箱梁独塔斜拉桥的涡激振动性能进行了风洞试验研究，发现来流上游侧人行道墙式防撞护栏是导致涡激振动发生的最主要原因，检修车轨道和检修道栏杆对竖弯涡振起放大作用；设置检修车轨道遮风板可以一定程度降低涡振振幅，高透风率的钢结构人行道防撞护栏能够有效降低竖弯涡振振幅［11］。王骑等［12］、宋锦忠等［13］也分别对此类断面的涡激振动性能展开过针对性研究。

上述研究多针对某种特定主梁断面的涡振特性，存在“一桥一议”的状态，缺乏系统分析，半开口类断面涡激振动性能变化规律尚不能确定。同时，根据已有的研究可知涡激振动对主梁断面形式十分敏感，其中一个重要的影响因素是主梁截面的宽高比。Shiraishi等［14］和Deniz等［15］对类桥梁断面绕流特性研究发现：当断面宽高比增大时，主梁周围涡脱结构变为尾端涡脱，且为双剪切层涡振驱动机制。但是，已有的研究大多基于宽高比小于12的主梁结构，当宽高比继续增大时绕流结构特性不得而知，有必要基于风洞试验对此展开进一步研究。本文针对宽高比13.57的宽幅半开口主梁断面，基于节段模型风洞试验，讨论攻角和阻尼比等因素对其涡振性能的影响，在此基础上总结半开口类断面主梁的涡振性能变化规律，初步探究半封闭箱梁涡激振动的诱因，为工程应用提供依据。

1 涡振性能试验分析

1.1 主梁截面形式

以某主跨420 m的单跨悬索桥为工程背景，该桥主梁为带风嘴的箱型双主梁＋钢横梁＋混凝土桥面板的开口叠合梁，为半开口断面形式，其有效宽度为38.00 m，高度为2.80 m，宽高比为13.57。其中，风嘴角度为95°，钢主梁宽度为7.80 m，横隔板宽度为22.40 m。主梁断面如图1所示。

图1 主梁断面（单位：m）Fig.1 Cross section of main girders（unit：m）

1.2 风洞试验

为研究主梁的涡振特性，制作节段模型进行风洞试验。模型几何缩尺比为1∶50，长度为2.095 m。主梁模型框架采用优质木材制作，主梁外形通过高性能木材蒙皮制作，梁上内、外侧防撞护栏等附属构件为通过数控雕刻机制作的工程塑料板，结构模型整体刚度满足试验要求。通过8根弹簧将节段模型悬挂于洞壁外的支架上。为保证模型流场的二维特性，在其两端设置端板。节段模型如图2所示。

图2 风洞中的节段模型Fig.2 Section model in wind tunnel

节段模型试验的主要参数如表2。根据《公路桥梁抗风设计规范》（JTG／T 3360-01—2018）［16］，叠合梁阻尼比取1%；成桥状态主梁竖向、扭转的风速比分别为5.3，5.4；施工状态主梁竖向、扭转的风速比均为4.7。

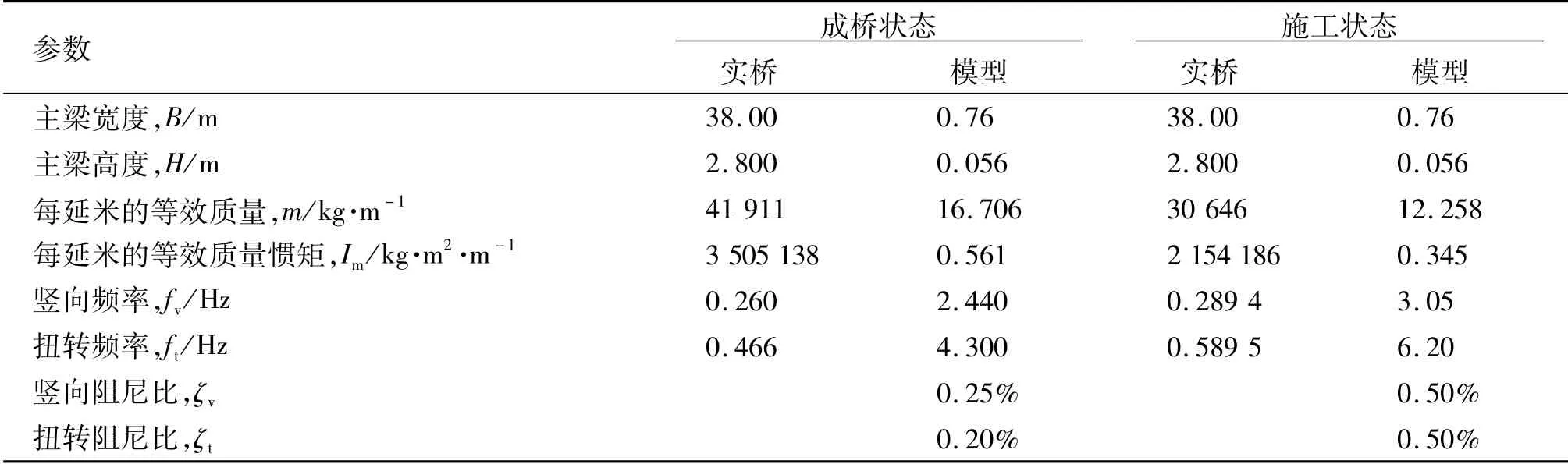
表2 节段模型主要参数Table 2 Main parameters of section model

1.3 试验结果

攻角分别为0°，±3°和±5°时，成桥状态主梁断面的涡振性能结果如图3所示。图3中横轴为无量纲风速V＝U／fB，其中U为来流风速，U，f，B均为实际桥梁参数；纵轴为无量纲振幅η＝1000y／B，其中y为实桥竖向涡振振幅。

由图3（a）可知，主梁在攻角为＋3°和＋5°时均出现竖向涡振，攻角为0°，-3°和-5°时未出现涡振（数据未列出）；主梁断面出现了2个涡振区，涡振区较接近且其无量纲风速区间分别为0.5～1.0和1.2～2.2；不同攻角时，主梁断面第1个涡振区的无量纲竖向涡振最大振幅基本一致，均为1.8左右；攻角为＋3°和＋5°时第2个涡振区的主梁无量纲竖向涡振最大振幅分别为3.94和8.82，攻角为＋5°时的主梁最大振幅比＋3°时增大约119%。对比风攻角为0°时的结果可知，该断面涡激振动性能存在明显的风攻角效应，即：0°攻角时未发生涡激振动，正攻角时主梁的竖向涡激振动振幅明显增大，与以往的针对其他典型断面风攻角效应一致。试验结果也证明，单纯的半封闭断面形式并不能激发主梁竖向涡激振动。

由图3（b）可知，主梁扭转涡振也出现2个涡振区，攻角为＋3°和＋5°时主梁扭转涡振最大振幅分别为0.59°和0.60°。需要说明的是，试验时主梁扭转涡激振动阻尼比为0.20%（远小于我国规范规定1.00%），当阻尼比增加到0.80%时，扭转涡激振动最大振幅约为0.2°，此时涡激振动振幅已远小于规范允许值，主要是竖向涡激振动的影响，因此后续主要分析竖向涡激振动性能。

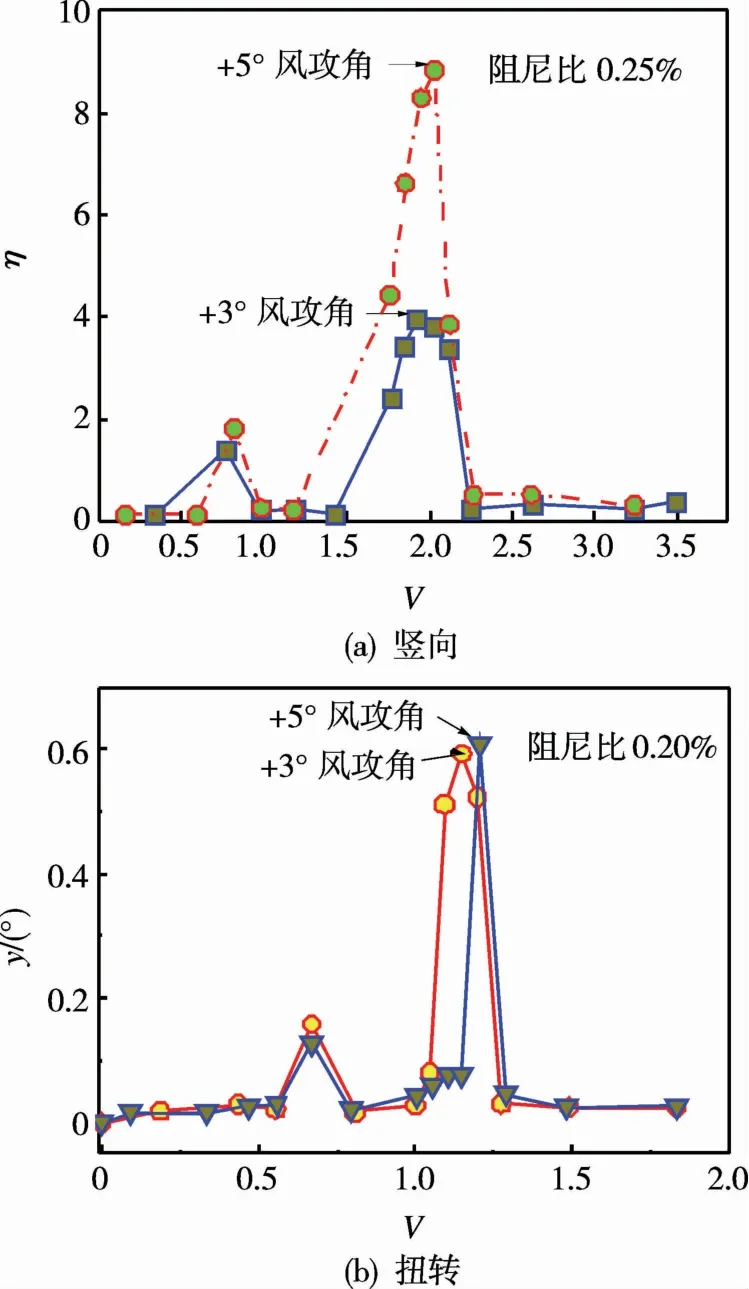
图3 主梁断面成桥状态涡振振幅Fig.3 Vortex-induced vibration amplitude of main girder sections under service status

攻角分别为0°，±3°和±5°时，竖向及扭转阻尼比为0.50%，施工状态主梁断面的涡激振动完全消失，具体结果如图4所示。对比成桥及施工状态的主梁参数可知，施工状态一阶频率略有增大，但质量及质量惯性矩减小，由此推测：在相同攻角工况下，人行道栏杆是引起主梁涡激振动的主要影响因素。

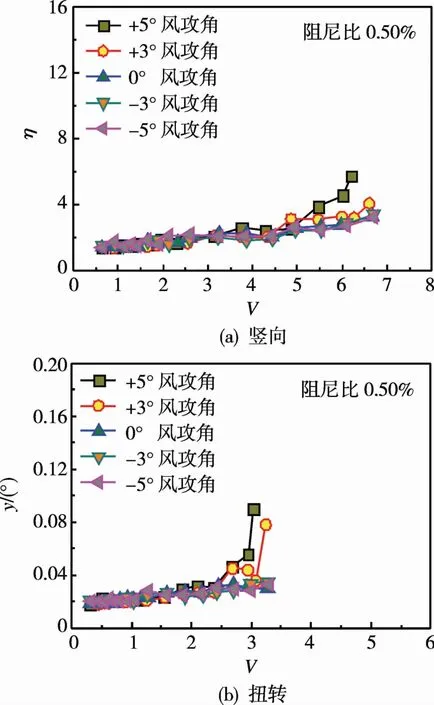
图4 主梁断面施工状态涡振振幅Fig.4 Vortex-induced vibration amplitude of main girder sections under construction status

对比成桥及施工状态主梁在不同攻角时的竖向涡激振动试验结果，成桥状态 0°攻角时成桥态主梁并未发生涡激振动，不同攻角下施工状态主梁（无栏杆）也并未发生涡激振动，推测单独的人行道栏杆影响或风攻角效应均不确定能否引起涡激振动，二者叠加作用下可能会引发涡激振动。

为分析阻尼对宽幅半封闭箱梁竖向涡激振动性能的影响，图5显示了4种不同阻尼比（0.25%，0.55%，0.80%和1.00%）工况下的无量纲涡振振幅，图中ηmax代表无量纲竖向涡振最大振幅。从图5可知，主梁断面无量纲竖向涡振最大振幅随阻尼比的增大而减小。攻角为＋3°，阻尼比为0.25%，0.55%，0.80%和1.00%时，无量纲竖向涡振最大振幅分别为3.94，2.48，1.42和1.10，与阻尼比为0.25%的振幅相比，无量纲最大振幅依次减小37%，64%和72%。攻角为＋5°，阻尼比为0.25%，0.55%，0.80%和1.00%时，无量纲竖向涡振最大振幅分别为8.82，6.57，4.26和3.71，与阻尼比为0.25%的振幅相比，无量纲最大振幅依次减小26%，52%和58%。同时，不同阻尼比条件下主梁竖向涡激振动最大振幅随阻尼比近似呈线性变化。阻尼比相同的条件下，＋5°攻角时主梁的无量纲竖向涡振振幅更大。随着阻尼比逐渐增大，＋5°攻角与＋3°攻角时主梁的无量纲竖向涡振振幅差距逐渐减小。

图5 不同阻尼比下的竖向涡振振幅Fig.5 Vertical vortex-induced vibration amplitudes at different damping ratios

2 半开口类断面的涡振性能综合分析

为进一步分析半封闭箱梁涡激振动性能，表3统计了部分半封闭箱梁涡激振动试验结果。图6给出了主梁一阶频率与桥梁跨度的变化关系，其中横轴为主梁主跨跨度，纵轴为频率值。可以看出，随着桥梁跨度的增大，主梁频率呈现线性减小的趋势。因桥梁主梁宽度为38.00 m，高度为2.80 m，宽高比13.57，与表3中其他主梁相比，宽高比明显偏大，主梁扭转刚度可能偏小，因此与同类型其他桥梁相比，该桥的扭转频率略微偏低。

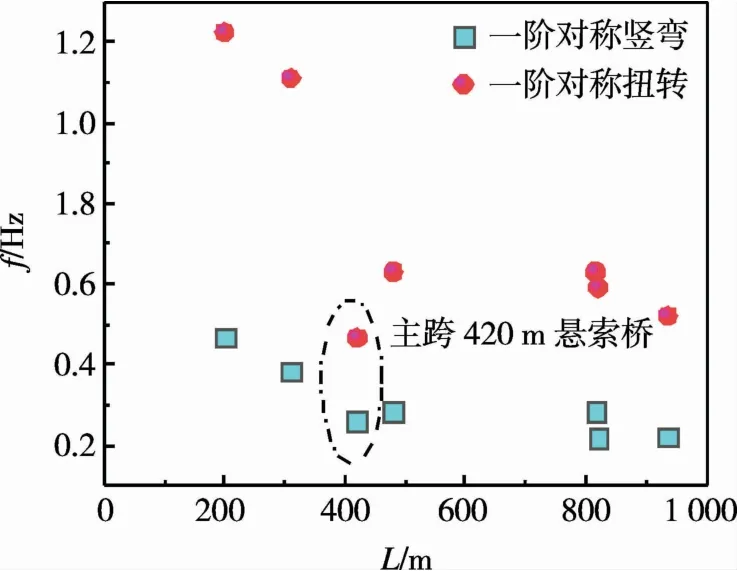
图6 主梁一阶频率随主跨变化Fig.6 The first-order frequencies of main girder varying with the main span

由表3可知，几座桥梁主梁的宽高比在10～12之间，且风嘴角度在60°～70°之间，斜腹板倾角范围15°～24°，且涡振区间大部分在15～20 m／s，主梁竖向涡激振动振幅最大值范围约为0.3～0.5 m，极个别主梁出现了扭转涡激振动，且扭转涡振区间对应风速在30 m／s以上，故此处暂未列出，只对比竖向涡激振动性能。

表3 部分半封闭箱梁涡激振动结果统计（＋5°攻角）Table 3 Results of vortex-induced vibration responses for some semi-closed girders（＋5°wind attack angle）

为进一步理解阻尼、质量、攻角等因素对主梁断面涡激振动性能的影响，图7给出了不同攻角时主梁无量纲竖向涡振最大振幅随Scruton数Sc的变化曲线，图中结果除标注外，均为＋5°攻角结果。Sc＝4πMξ／（ρD2），式中ξ为主梁断面试验时的阻尼比；D为主梁断面特征尺寸，此处取主梁宽B；M为主梁断面等效质量；ρ为空气密度。

由图7可知，除个别窄幅主梁涡激振动振幅较小，大部分半封闭箱梁涡激振动最大振幅随Sc数的增大而逐渐减小，总体呈线性变化且可用函数较好拟合，可为同类型桥梁涡激振动振幅值估算提供依据。同时，＋3°攻角时主梁涡激振动最大振幅较＋5°攻角时略微偏小，但符合总体变化规律。

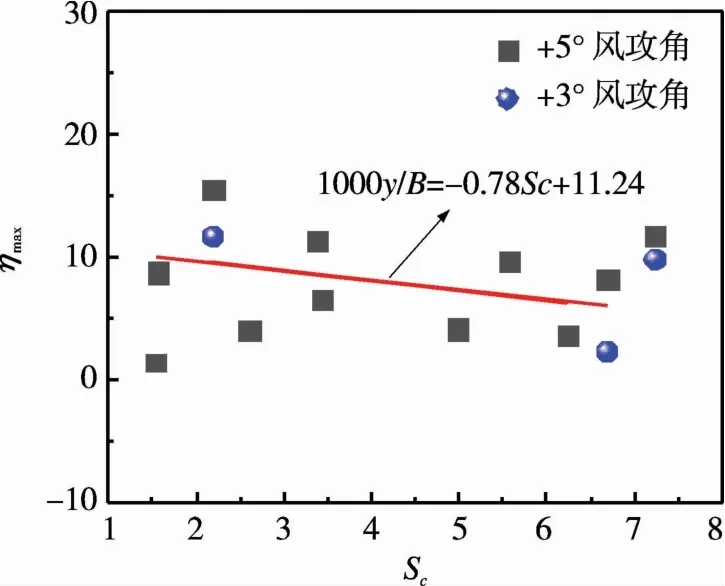
图7 主梁无量纲竖向涡振最大振幅随Sc数变化Fig.7 Variations of themaximum amplitudes of non-dimensional vertical vortex-induced vibration of main girders with Sc

3 涡激振动诱因初探

对比第1节中主梁成桥及施工状态的涡激振动试验结果，可知试验时施工状态主梁Sc数为2.28，主梁涡激振动消失，单纯的半封闭箱梁并未发生涡激振动，推测桥面栏杆是该类主梁涡激振动的主要诱发因素，半封闭断面形式对主梁涡激振动起进一步放大作用。方根深［6］试验时也发现，去掉栏杆或去掉来流上游侧栏杆时，主梁均未发生涡激振动，来流上游侧的检修道栏杆是诱发半封闭箱梁涡激振动的主要因素，检修车轨道等因素会起一定的放大作用，并提出在栏杆处布置水平翼板或抑流板可较好抑制主梁竖向涡激振动。Nago［12］认为栏杆对主梁竖向涡激振动的自激涡激力影响较小，阻尼力明显减小是诱发主梁涡激振动的主要原因。

采用FLUENT软件模拟了主梁竖弯第二个涡振区涡激振动，计算模型缩尺比选为1∶50，＋5°风攻角下进行，风速为3.57 m／s（竖向涡振最大振幅对应风速），采用k-wSST湍流模型及壁面函数。方程组求解时采用SIMPLE算法，收敛项残差控制在1×10-6、时间步长设置为2.0×10-4以确保柯朗数小于5，雷诺数与主梁节段模型试验保持一致。数值模拟计算域为38B×8B（B为主梁截面宽），截面中心距前后边界分别为14B和24B，距上下边界均为4B。网格划分时，在远离断面区域采用稀疏网格，在结构断面周围进行网格加密，靠近断面第一层网格厚度为0.000 2 m，网格总数为50万，保证y＋值小于5。断面和附属设施表面边界为无滑移壁面边界，入口为均匀来流速度入口，来流速度U为3.57 m／s；出口为压力出口边界条件，上、下边界均为壁面边界条件。

图8为主梁断面在3.57 m／s计算风速下的气动升力频谱图，频谱图中共存在2个卓越频率，其值分别是2.6 Hz与5.2 Hz，呈明显的倍频现象。通过风洞试验得到主梁在＋5°风攻角下竖弯涡振风速为3.57 m／s，由此可计算得到对应的斯托罗哈数St为0.038。通过数值模拟计算得到的斯托罗哈数与风洞试验数据相比，误差为5.0%，表明本文的模拟结果可较准确地再现断面的漩涡脱落与发展情况。

图8 升力及其频谱图Fig.8 Lift force and the corresponding spectrum

图9为＋5°攻角时半封闭箱梁周围的瞬时涡量及平均流线图。从图9可以看出，＋5°攻角时，来流在主梁迎风侧风嘴处发生分离，由于正攻角效应及桥面人行道栏杆的影响而产生较大的旋涡，并在主梁断面上部出现3个较大尺寸的旋涡，同时另一部分来流沿风嘴下斜腹板运动，并在主梁的半开位置产生2个较大尺寸的旋涡，主梁上、下部位的旋涡不断运动，在尾部发生周期性脱落，半封闭箱梁涡激振动为运动涡导致的，并掺杂有卡门涡街，主梁尾部呈明显的双旋涡驱动机制。

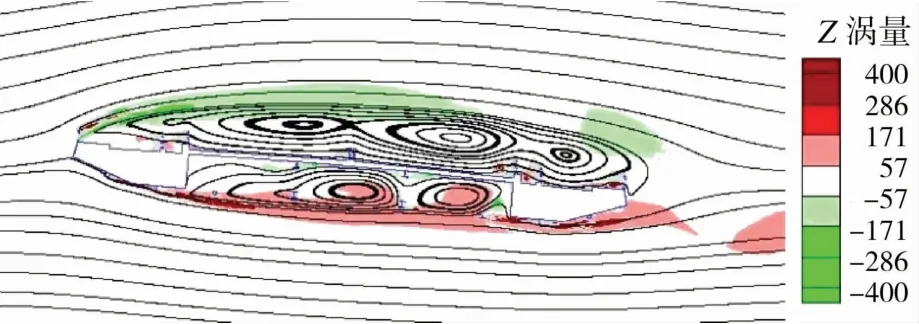
图9 ＋5°风攻角时主梁的涡量与迹线图Fig.9 The vorticity magnitude and trace diagram around girder at＋5°wind attack angle

4 结论

在半封闭箱梁涡激振动风洞试验研究的基础上，对比不同尺寸参数主梁的竖向涡激振动性能，分析了涡激振动的主要诱因，并初步探究了其绕流结构，得到以下结论：（1）半封闭箱梁在＋3°和＋5°时均出现竖向涡振，攻角为0°，-3°和-5°时未出现涡振；主梁断面出现了2个涡振区，攻角为＋5°时的主梁竖向最大振幅比攻角为＋3°时增大约119%。（2）半封闭箱梁竖向涡激振动性能同样存在明显的风攻角效应，单纯的半开口断面形式并不能激发主梁竖向涡激振动。人行道栏杆及风攻角效应是引起半封闭箱梁竖向涡激振动的主要因素。（3）半开口类主梁涡激振动最大振幅随Scruton数的增大而逐渐减小，总体呈线性变化且可用函数较好拟合，可为同类型桥梁涡激振动振幅值估算提供依据。