等质量5卫星中心构型模型与计算

陈 剑 李培茂 张晓勇 谢馥励 毕 鹏

（1.西南科技大学数理学院 四川绵阳 621010；2.四川中烟工业有限责任公司绵阳卷烟厂 四川绵阳 621000；3.西南科技大学制造科学与工程学院 四川绵阳 621010）

人类对星星（天体）的观察和研究已有几千年历史并将一直持续进行。天体力学的诞生使人们对星星（天体）的研究进入新的历史阶段。牛顿N体问题是天体力学的基本问题之一，作为研究天体系统运行的一种力学模型，对它的研究有助于人类对自然界中基本天文现象的理解和预测，如海王星的发现。中心构型是天体力学上一个古老且重要的问题，对中心构型的研究在理解N体问题的复杂性方面起着“中心”作用［1］，对人们解释天体的运行具有非常重要的意义，如天体的碰撞、膨胀、周期轨道以及同形运动等，有太空“停车位”之称的著名的拉格朗日点就是中心构型一个非常显著的应用。另外，中心构型能生成牛顿运动方程的唯一显式解，决定碰撞附近天体的行为以及影响积分流形的拓扑结构等［2］。

1859年，Maxwell构造土星环模型时，近似地把土星环看作是由等质量且位于正n边形的顶点上的n个无穷小天体（卫星）组成，它们围绕中心的土星做刚体旋转。这是人们首次考虑限制1＋n体问题的中心构型，即关于一个大的天体以及n个无穷小天体（卫星）的中心构型问题，对它的研究可用于解释、预测及模拟小天体（卫星）的运行及相互影响等。

Moeckel［3］研究了n颗卫星中心构型及其线性稳定性，并给出了一个判定准则。Casasayas等［4］给出了n颗卫星中心构型模型的一个新的推导，并且在卫星质量相等的情况下证明了对于足够多的卫星只有唯一的构型。Albouy等［6］证明了等质量4卫星中心构型模型一定对称。Oliveira［8］证明了若4颗卫星中的某两颗卫星对径，构型一定是对称的，且这两颗卫星不能相邻，而另外两颗卫星质量相等，同时还得到了构型的个数。Deng等［10］研究了4卫星对称中心构型。Chen等［11］研究了4卫星的对径中心构型，发展和推广了Oliveira的结果。古往今来，中心构型以及限制1＋n体问题的中心构型引起了众多专家和学者的关注，并得到了大量的建设性成果［12-20］。

1 n颗卫星中心构型模型

设无穷大天体位于平面直角坐标系的原点上且质量为1，n个无穷小天体（卫星）位于qk处且质量为mk＝εμk（k＝1，2，…n），其中μk＞0，ε＞0为趋于零的无穷小参数。对于平面n颗卫星的所有中心构型，卫星都位于一个以无穷大天体为中心的共轨圆上。若以从原点到qi的半径和原点到qi＋1的半径之间的夹角θi作为坐标（第n颗与第1颗之间形成的夹角记为θn），n颗卫星的中心构型模型（系统）为：

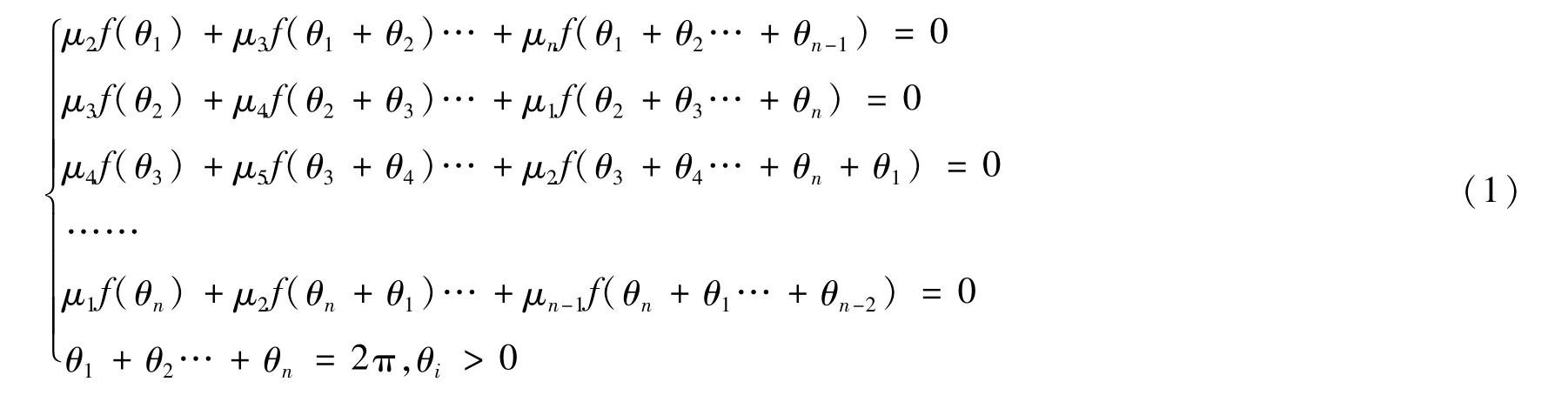
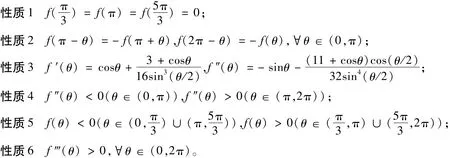
函数f（θ）的图像及函数f′（θ）的图像如图1、图2所示。

图1 函数f（θ）的图像Fig.1 Image of function f（θ）

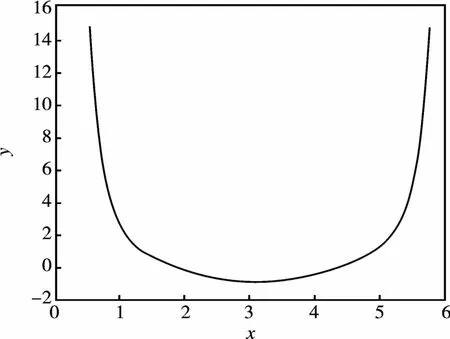
图2 函数f′（θ）的图像Fig.2 Image of function f′（θ）

本文给出了等质量对径5卫星中心构型模型，即5颗卫星质量相等且位于以无穷大天体为圆心的共轨圆上，其中某两颗卫星位于该圆的一条直径的两端，即对径。应用部分对称条件，得到对称模型及其解的情况，再从特殊到一般，讨论了模型的解。

2 等质量对径5卫星中心构型模型

当5颗卫星的质量相等时，模型（1）演化为：

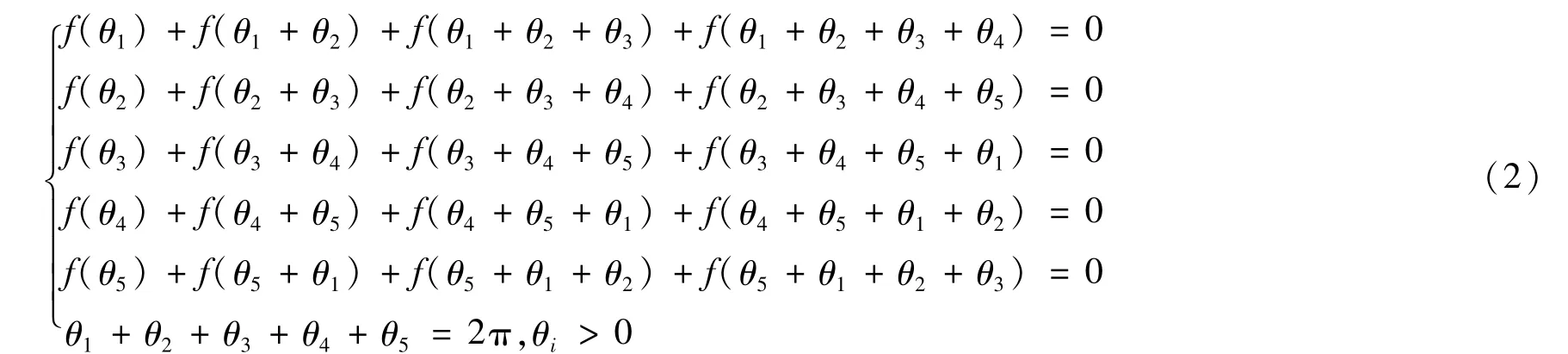
下面分别针对相邻卫星对径和相间卫星对径两种情况研究模型（2）。

2.1 相邻两卫星对径

不失一般性，假设θ1＝π，θ2＋θ3＋θ4＋θ5＝π，如图3所示。注意到f（π）＝0，f（π-θ）＝-f（π＋θ），f（2π-θ）＝-f（θ）以及θ5＝π-θ2-θ3-θ4，模型（2）转化为：

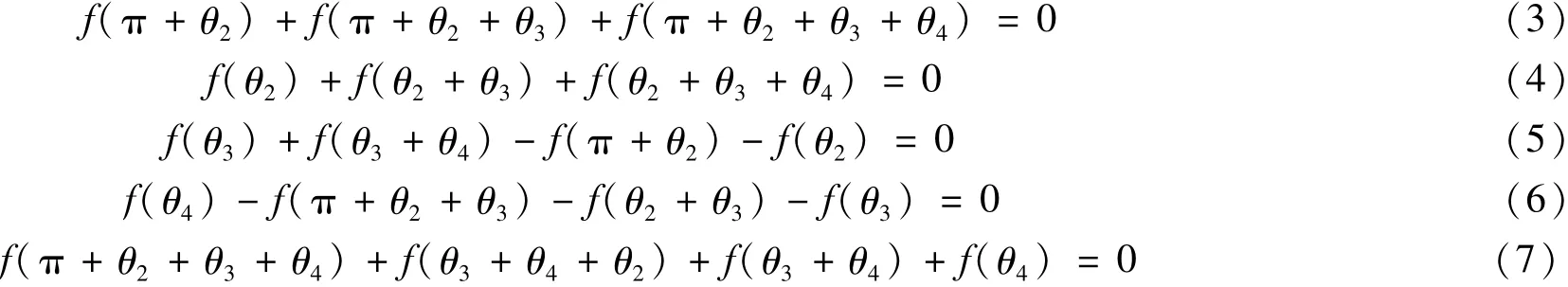
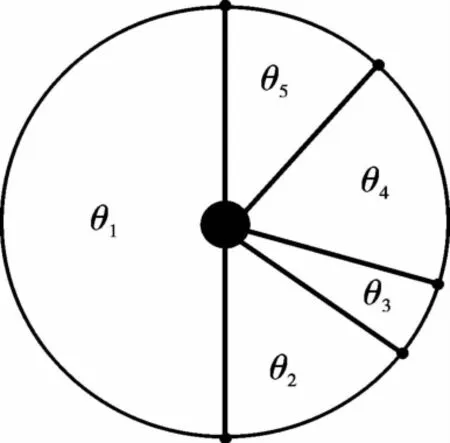
图3 相邻两卫星对径Fig.3 Consecutive satellites being diametrically opposite

2.1.1 对称模型

由于该系统较复杂，首先考虑θ3＝θ4时的特殊情况，此时方程（6）变为f（π＋θ2＋θ3）＋f（θ2＋θ3）＝0，根据f（θ）的性质2f（π-θ）＝-f（π＋θ），有f［π-（θ2＋θ3）］＝f（θ2＋θ3）。令即可得，易求得，所以由于，因此而θ3＝θ4，所以θ5＝θ2，此时模型对称。又由方程组式（3）-式（7）等价于以下方程组：

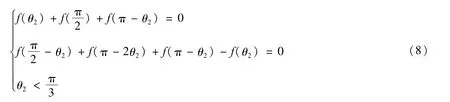
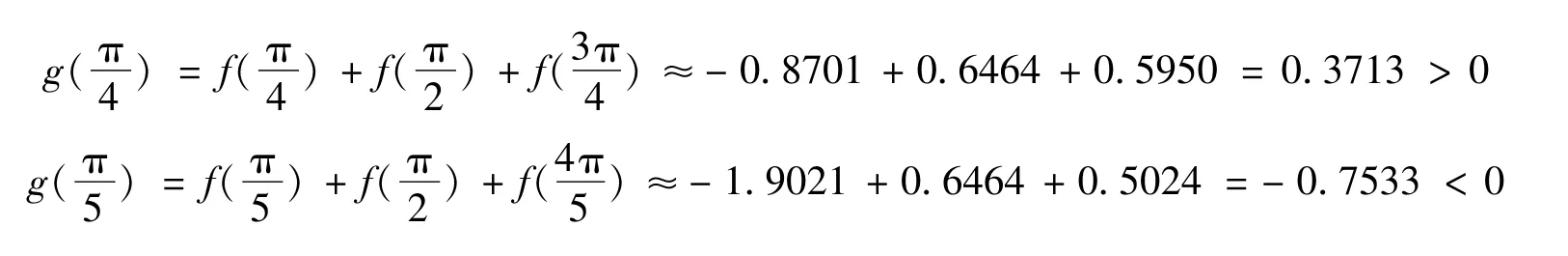
即g（θ）在内只有唯一零点，且属于

2.1.2 一般模型

因为在等质量条件下，对称模型是最有可能产生中心构型的情况。而前面已经证明了对称情况不存在中心构型，所以推测一般模型也不存在中心构型，即方程组式（3）-式（7）也是无解的。由于模型的复杂性，理论分析较为困难，利用MATLAB编程解方程组式（3）-式（7），可得到当3，4，5）时，方程组确实无解，也就是说当卫星质量相等时，不存在某相邻两卫星对径的中心构型。

2.2 相间两卫星对径

不失一般性，设θ1＋θ2＝π，θ3＋θ4＋θ5＝π，如图4所示。注意到f（π）＝0，f（π-θ）＝-f（π＋θ），f（2π-θ）＝-f（θ）以及θ2＝π-θ1，θ5＝π-θ3-θ4，则模型（2）转化为：

图4 相间两卫星对径Fig.4 Alternate satellites being diametrically opposite

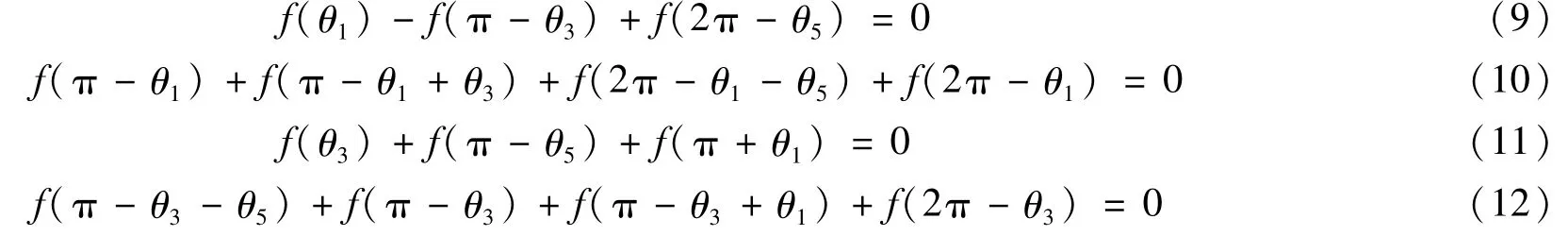
这里模型（2）的第5个方程可由前4个方程得到，因此消去。因θ3＋θ4＋θ5＝π，所以θ3，θ5中至少有一个小于

2.2.1 对称模型

又由式（9）和式（11）可得：f（θ3）-f（π-θ3）＝f（θ5）-f（π-θ5）。

令l（θ）＝f（θ）-f（π-θ），l′（θ）＝f′（θ）＋f′（π-θ），l″（θ）＝f″（θ）-f″（π-θ），由于f‴（θ）＞0，∀θ∈（0，2π），即f″（θ）在（0，2π）内单调递增。若，此时θ＜π-θ＜π，就有f″（θ）＜f″（π-θ），即l″（θ）＜0，所以l′（θ）在上单调递减。而，即l′（θ）＞0，所以上单调递增。由于，可得θ3＝θ5，即构型是对称的。此时，式（9）-式（12）等价于如下方程组：

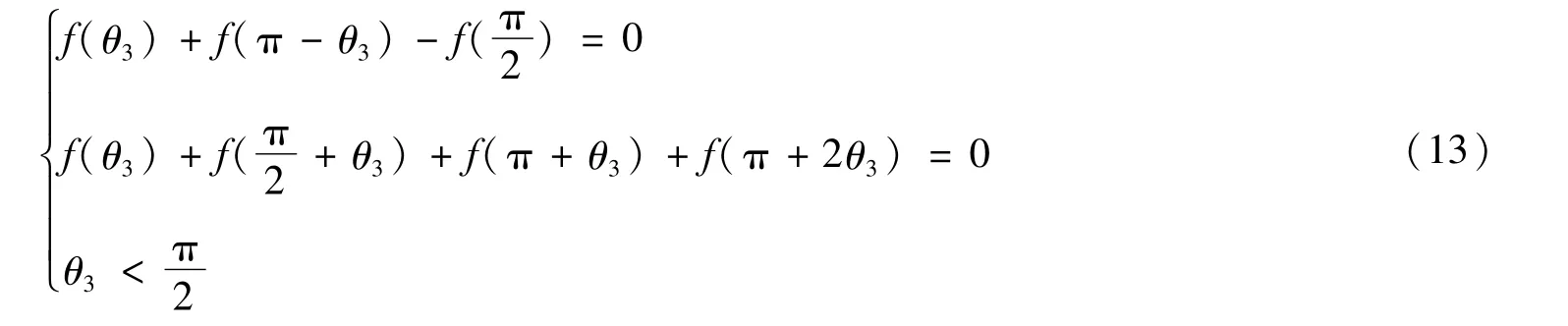
所以m（θ）＝0在内存在唯一解且属于

2.2.2 一般模型

同样，因为在等质量条件下，对称模型是最有可能产生中心构型的情况。而上面已经证明了对称模型不存在中心构型，所以可推测一般情况下也不存在中心构型，即方程组式（9）-式（12）也是无解的。由于模型的复杂性，理论分析较为困难，利用MATLAB编程解方程组式（9）-式（12），可得到当或时，系统确实无解，亦即当5卫星质量相等时也不存在相间两卫星对径的中心构型。

3 结论

应用对称模型方法及计算机仿真建模，从特殊到一般，研究了等质量对径5卫星中心构型。证明了当5颗卫星质量相等且其中某两颗卫星（无论相邻还是相间）对径时，中心构型方程都无解，即不存在等质量对径5卫星中心构型。文中所用方法及所得结果，丰富了对限制1＋n体问题中心构型的认识，为人们研究和探索卫星及人造卫星在空间的分布提供了有意义的理论依据。