永磁同步直线电机自适应控制研究策略

张福特

（江南大学 物联网工程学院，无锡 214000）

永磁同步直线电机是一种无须借助于任何传动装置就能够将电能转化为动能的直线电机，是直线驱动控制技术中最典型的应用案例。得益于优良的机械性能，它在数控机床、工业机器人以及半导体加工等领域发挥着重要作用。但是，如何精密控制永磁同步直线电机，仍面临着较大挑战。

1 永磁直线同步电机自适应控制策略

1.1 永磁直线同步电机的d-q坐标数学模型

对于永磁直线同步电机来讲，一般认为它的电枢中d轴和q轴具有大小相同的电感，即Lq=Ld=L[1]。以旋转电机的d-q轴模型作为参考，通过计算可以得出直线电机在d-q坐标系下的电压方程。

直轴电压方程为

交轴电压方程为

电磁推力方程为

机械运动方程为

式中：L为电枢电感；p为极对数；R为电枢电阻；ψf为定子磁钢在电枢中的耦合磁链；v为电机运转速度；M为动子和负载质量；B为粘滞摩擦系数；Fm为电磁推力；Fd为负载阻力。参照以上方程可以画出永磁同步直线电机的d-q坐标系数学模型，如图1所示。

图1 永磁同步直线电机数学模型图

1.2 永磁直线同步电机矢量控制

矢量控制包含id=0、cosφ=1、最大推力/电流比控制以及弱磁控制等几种不同的类型。其中，id=0矢量控制是一种应用最广泛的控制方式。采用这种方式需要先将d轴电流设定为0，使得电机定子的电流和q轴电力相同。cosφ=1主要是利用对d-q轴电流的控制，实现将电机定子电流和定子电压保持同一方向。但是，这种控制方式会使电磁推力和电流之间呈现出非线性化关系，相较于其他控制方式，在同样电流大小的情况下，对应的推力会减小。在d轴、q轴具有相同电感时，这种控制方式的原理和id=0控制方式是相同的，但存在在大推力状态下功率因数较低的缺陷。结合本文研究对象和永磁同步直线电机的控制方式，本文采用id=0控制方法。

1.3 永磁直线同步电机初始位置检测

永磁同步直线电机的电磁推力Fe可以表示为

式中：kf为推力常数；Fs为电机定子的磁动势；FPM为电机永磁体磁动势；δ为定子磁动势和永磁体磁动势之间的夹角。结合所列电磁推力方程，在两个磁动势之间的夹角为零时，对应的电磁推力也为零。要想得到电机的初始位置，式中只需给定一个具体的电压矢量推动电机移动，在δ逐渐达到零时，电磁推力也会减小至零，从而获得电机的初始位置[2]。

1.4 永磁同步直线电机的MATLAB/Simulink模型

结合式（1），构建直线电机的直轴电压方程模型。结合式（2），构建直线电机的交轴电压方程模型。结合式（3）和式（4），构建直线电机的机械运动方程模型[3]。将各个模块进行有机整合，可以得到永磁同步直线电机的仿真模型，如图2所示。

图2 永磁同步直线电机的仿真模型

2 基于干扰观测器的控制设计与仿真

2.1 控制设计

采用非奇异终端滑模（Non-singular Terminal Sliding Mode，NTSM）控制完成永磁同步直线电机位移系统的控制器设计[4]。利用干扰观测器的前补偿对控制器进行设计的数学模型为

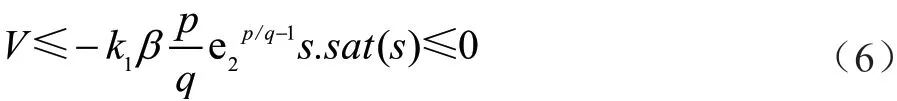
式中：k1为常数；β＞0；e2为速度误差；p、q分别为正奇数；s为NTSM滑膜面；sat()为饱和函数。

结合李雅普诺夫理论可以得出，该控制系统的特性能够保持一致且稳定。设计的基于非线性干扰观测器（Nonlinear Disturbance Observer，NDO）的NTSM控制系统结构如图3所示。

图3 基于NDO的NTSM控制系统结构

2.2 仿真研究

通过用MATLAB/Simulink两种仿真工具对上述3种针对永磁同步直线电机的控制方式进行仿真实验，分析测试结果。电机初始位置数据信号通过正弦曲线y=0.2siny(t)m计算获取（其中t为时间，m为位移），在仿真实验过程中设定扰动力数值为10 N，仿真实验结果如图4和图5所示[5]。图4为电机位置跟踪曲线，图5为电机位置跟踪误差曲线。仿真实验中，3种控制方式都能做到对参考信号的有效跟踪。此外，仿真结果表明，比例积分（Proportional Integral，PI）控制系统和NTSM控制系统两种模式的稳态误差较大，而NTSM+NDO控制系统的稳态误差较小，但也存在一定的误差值。

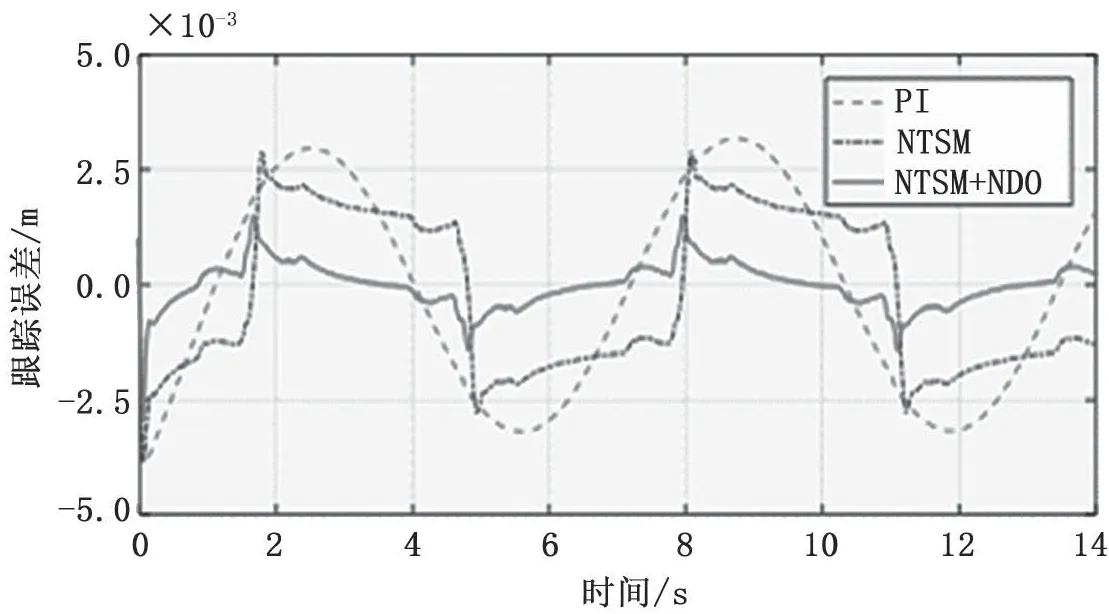
图4 PI、NTSM、NTSM+NDO控制位置跟踪曲线

图5 PI、NTSM、NTSM+NDO控制方式的位置跟踪误差曲线

3 结语

通过以非线性干扰观测器为基础的控制策略，设计出NTSM控制器，并采用饱和函数对滑块的振动和抖动进行抑制，采用NDO对NTSM控制器进行补偿，以提升稳定性。通过MATLAB/Simulink仿真和对比，结果表明永磁同步直线电机自适应控制方式在电机的动态响应、稳态误差方面均具有优异性能。