工业机械臂的模型设计与运动分析

樊宏升

（北京天玛智控科技股份有限公司，北京 100013）

随着工业逐渐步入4.0时代，大幅提高了社会生产力，单纯的人力已经无法满足生产快速性与标准化的需求。特别是针对一些危险的工作环境，需要使用自动化机械设备取代人工进行更高效的生产。机械臂具有普适性，是生产线上代替人工的主要设备。

工业机器人作为机器人大家族的重要一员，主要指面向工业生产的或者有多个自由度的机器人或者机械臂。一般来说，工业机器人主要由机器人本体、操控机器人工作的控制器、伺服驱动系统及传感系统组成。机器人不仅可以自动控制，也可以通过编程完成各工位的相应任务。在当今工业生产中，机械臂在提高产品良率和生产效率方面扮演了十分重要的角色。

1 机械臂运动控制算法研究现状

机械臂轨迹跟踪控制是机器人控制中最重要的部分。在应用机器人的过程中，既要系统功能完善，又要系统性能良好。前者体现在具有相对宽泛的运行空间范围，后者表现在使用过程中能够满足人们的需求。机械臂具有和一般机器人相同的运动学和动力学特点，即变量多、时变性大、耦合性高等，运行中存在很多不确定因素，对整个控制系统的稳定性会产生很大影响。以五轴机械臂作为研究对象，基于设计的结构与尺寸进行运动学和动力学分析，并通过计算得到的运动学模型对机械臂进行实际仿真，规划其运动轨迹，分析其空间运动范围。

2 模型设计与计算

2.1 模型设计

本机械臂是一种关节坐标式机器人，如图1所示。它主要由旋转底座部分（肩膀）、大臂部分、前臂部分及机头部分（手腕部分）4部分组成。

图1 机械臂模型

2.2 各个关节的力矩估算

各个关节的动力参数是选择电机型号和减速器减速比的重要依据。根据机械臂动力学的相关知识，完整的机器人动力学方程为[1]

式中：q、q˙、˙˙q分别为广义关节坐标角度、速度和加速度矢量；M(q)为关节空间惯性矩阵；C为科里奥利和向心耦合矩阵；F为摩擦力；G为重力载荷；Q为关节驱动力矩；W为施加在末端执行器的外力；J(q)为机器人的雅可比矩阵[2]。

为估算每个关节的最大力矩，假定各个关节的重量都集中在关节理论中心点，各个连杆的重量都集中在连杆中间。计算静力矩时，机械臂主要受到重力产生的力矩作用，将机械臂拖动至产生最大力矩的位置，如图2所示。

图2 机械臂伸展图

机械臂位于最长伸展距离时，夹持处与大臂电机的垂直距离为1 091 mm，近似为1.1 m，计算可得大臂驱动关节距离计算质心距离为0.55 m。大臂质量为2 kg，前臂质量为1.54 kg，手腕部分质量为2.5 kg，设计指标夹取的物件质量为2 kg，此时前臂驱动关节距离最远处距离为685 mm，计算可得前臂驱动关节距离计算质心距离为0.34 m。前臂质量为1.54 kg，手腕部分质量为2.5 kg，设计指标夹取的物件质量为2 kg，则第3个前臂驱动关节的计算力矩为

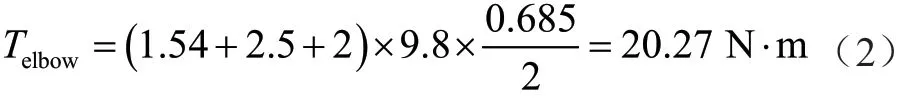
旋转底座电机与腕部旋转电机驱动部分不受重力扭矩，主要是加速度扭矩作为负载驱动整个机械臂的旋转。这时最大扭矩等于转动惯量乘以角加速度，即

转动惯量的表达式为

机械臂的质量为8.04 kg，杆长为1.1 m。假设机械臂旋转底座最大角加速度为0.5 rad·s-2，此时旋转平台关节的最大扭矩值为

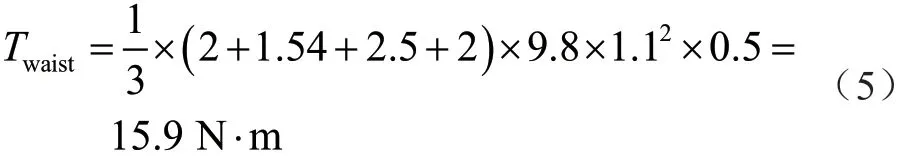
夹具质量为0.8 kg，夹持物件质量为2 kg，腕关节最大角加速度为1 rad·s-2，得出腕关节的最大扭矩值为

3 机械臂运动学分析

机械臂的运动学研究的是机器人的运动特性，从以下两个问题出发进行分析：一是正运动问题，即已知机械臂的连杆参数和关节变量，确定执行坐标系的位置和姿态；二是逆运动问题[3]，即已知机械臂连杆参数，给定目标为固定姿态，确定关节变量的大小。

3.1 机械臂的正运动学分析

正运动学的求解是根据已知关节变量求末端执行端相对于参考坐标系位姿的过程。正运动学对于轨迹规划与轨迹跟踪控制具有重要意义。通过改进D-H方法确立连杆参数的变换关系，将机器人极坐标系通过连杆齐次矩阵的连乘变换到末端执行器坐标系。利用这种变换可以求解机器人机械臂执行端相对于机器人基座的坐标系位置。三维向量n、o、a分别表示在基础坐标系下的向量相对变换。机械臂的正运动学方程可以根据表述的关系式求解，整理化简后为

3.2 机械臂的逆运动学分析

正运动学研究的是已知各关节角度[4]，计算执行器末端在笛卡尔空间中的位置。逆运动学主要研究的是给定执行器末端在笛卡尔空间中的位置，计算各个关节角的角度位置。

从工程应用角度来说，待给定各个关节角变量后，正运动学有特定唯一的解，此时末端姿态是唯一确定的。但是，逆运动往往有很多种结果。由于机器人结构设计，nz、oz、ax、ay都等于0，az=1。若末端的位姿已给定，可以求解关节变量θ1、θ2、θ3、θ4、θ5的值。

求解θ1为

求解θ2。在式（8）第一个等式两边依次分别乘有θ23为

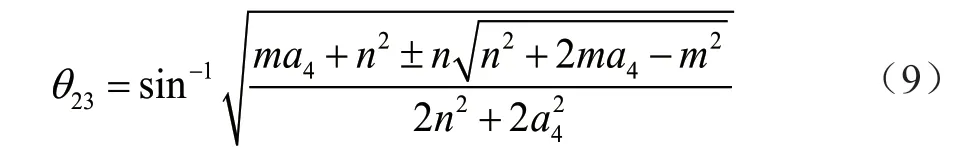
所以，有

求解θ3为

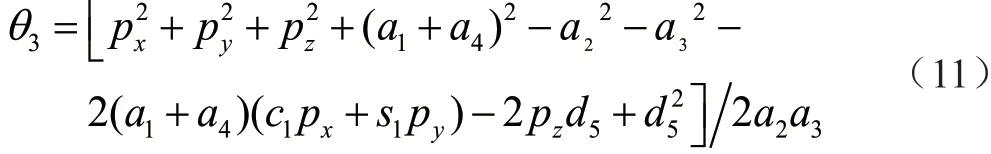
求解θ4。由提及的机械结构设计可知，θ4满足关系

于是，有

求解θ5。在式（8）第一个等式两边依次分别乘

4 机械臂运动学仿真分析

分析工业机械臂的运动学、动力学以及轨迹过程，可以使用基于MATLAB平台开发的机器人工具箱。

4.1 正运动学仿真

使用工具箱中的函数对工业机械臂建模并进行正运动学仿真，仿真结果见图3。可以给定角度进行示教调节，通过软件中的滑块控制角度的输入值，实现实时仿真控制。

图3 正运动仿真结果

4.2 逆运动学仿真

使用工具箱中的函数对机械臂求逆解。先给每个轴给定角度，计算此刻的变换矩阵，再将这个变换矩阵代入逆解函数，给定目标位置与姿态。

5 机械臂运动空间分析与仿真

使用蒙特卡洛方法分析工作空间。蒙特卡洛属于模拟统计方法[5]，是一种以概率统计理论为指导的数值计算方法。先在机械臂关节运动范围内生成n个随机值，关节角的取值为θi=θimin+(θimax-θimin)*rand(1,n)，再将随机生成的角度值代入计算得到的正运动学方程，最后在MATLAB中将机械臂的工作空间显示为点云图，取随机值个数为20 000进行计算分析。机械臂的工作空间如图5所示。使用蒙特卡洛方法在MATLAB中模拟其工作空间，使得实际机械臂的使用更加准确直观。

图4 逆运动仿真结果

图5 机械臂模拟工作空间

6 结语

本文阐述工业机器臂的应用领域与发展现状，主要介绍机械臂的机械结构设计，标定机械臂的主要设计尺寸，并通过计算机械臂每个轴承受的最大力矩范围来选定满足条件的步进电机与减速器。分析机械臂的运动学相关内容时，简单介绍机械臂坐标变换的基础知识、位姿在空间的描述、齐次坐标矩阵的平移与旋转。以设计的机械臂为研究对象，使用改进D-H方法对机械臂进行数字化建模，并对其正运动学与逆运动学进行分析，最后使用蒙特卡洛方法对机械臂的空间运动范围进行计算。现阶段，5自由度工业机械臂的动力学模型建立还存在一定误差，仍需寻找更加精确且有效的化简方法，使化简得到的动力学方程满足实时轨迹跟踪的控制要求。