圆弧轮廓铣削最大刀具补偿半径的确定方法

成建群

（苏州健雄职业技术学院 中德工程学院，太仓 215411）

数控刀具路径规划直接影响加工质量和加工效率。通过刀具半径补偿设置自动偏置，可避免大量轨迹偏置带来的复杂坐标计算[1]。另外，直接采用零件轮廓坐标编制刀具路径程序，可以利用刀补功能直接去除毛坯加工余量，简化编程过程[2]。对于复杂曲面加工，可以通过优化补偿方法适应曲面加工要求[3-4]。针对零件特殊表面的加工要求，可以充分运行刀具补偿原理，优化补偿算法，拓展刀具补偿的应用范围，改善加工质量[5-6]。在多轴加工过程中，刀轴矢量多变，但仍可实现刀具补偿[7-8]。刀具补偿编程是铣削过程中的基本方法，在运用刀具补偿编程时需要选用合适的刀具。刀具半径直接关系刀具的刚度，影响加工质量。刀具直径大，可以选用更高效的切削参数，提高加工效率，降低加工成本。

在铣削过程中，刀具半径与最小的零件轮廓半径有密切关系。零件轮廓半径小于刀具半径时，该轮廓不能进行切削。刀具补偿半径根据刀具半径设定，在不留加工余量的情况下，刀具补偿半径等于刀具半径；当留有加工余量时，刀具补偿半径大于刀具半径。所以，刀具最大半径小于等于刀具最大补偿半径。刀具最大补偿半径决定了刀具最大半径。在不考虑通过修改刀补来添加余量的情况下，刀具最大半径就是刀具最大补偿半径。

在数控加工过程中，通常以零件尺寸计算坐标，并添加刀具补偿指令完成编程，由数控系统自动计算偏置，完成零件轮廓加工。鉴于数控系统算法的原因，刀具半径将比零件轮廓半径更小。西门子840D系统是当前主流数控系统之一，应用广泛。本文以西门子840D系统为基础，研究零件轮廓半径与最大刀具半径之间的关系。

1 问题的提出

为了在保证一般性的同时简化问题，选用三轴铣削加工台阶外轮廓面零件进行研究。因外凸圆弧零件轮廓不影响刀具尺寸，这里仅仅考虑内凹槽圆弧零件轮廓，零件如图1所示。该图毛坯尺寸为80 mm×80 mm×20 mm，铣削台阶深度为2，三段圆弧凹槽直径均为Φ20 mm。左侧圆弧轮廓圆心在轮廓线上，中间圆弧轮廓圆心在轮廓线内侧，右侧圆弧轮廓圆心在轮廓线外侧。

图1 零件结构（单位：mm）

现选用西门子840D系统，刀具选用Φ16 mm铣刀，利用Vericut软件建立测试环境。测试环境主要设置如表1所示，控制系统选用sin840d。

表1 Vericut软件测试环境主要设置

仿真结果如图2所示，3个Φ20 mm圆弧轮廓仅仅完成了2个，其中1个并未按要求完成，仅表现为Φ16 mm刀具直径的轮廓。进一步可以查看刀路图，如图3所示，其中有1处出现折线，但并未出现Φ20 mm圆弧轮廓加工刀路。

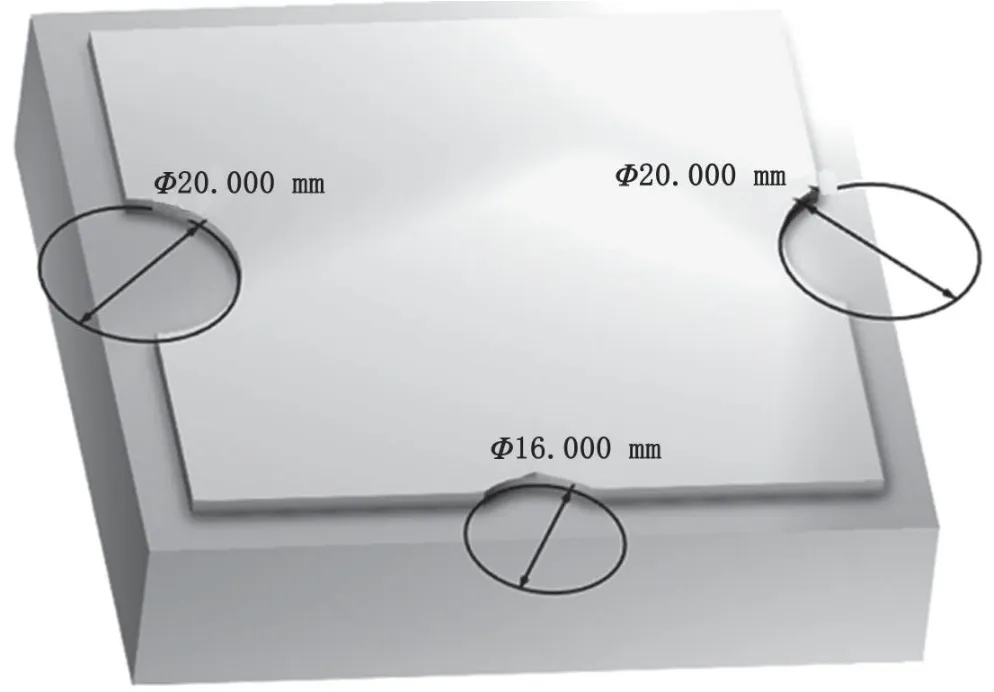
图2 Φ16 mm刀具仿真结果

图3 Φ16 mm刀具仿真刀路

可见，当圆弧轮廓圆心在轮廓线外侧或在轮廓线上时，刀具最大直径为圆弧轮廓直径；当圆弧轮廓圆心在轮廓线内侧时，刀具最大直径小于圆弧轮廓直径，具体数值需要建立数学模型进行分析。

2 数学模型建立

程序中按逆时针圆弧方向编制，坐标由A点到B点，圆心为O。因刀具偏置，A点时，刀具圆心向左和向下都偏移距离d。切线方向进入圆弧，进入圆弧第一个点A对应刀具中心O1，切线长度为d，由此可以得到刀具中心由K点沿切线进入圆弧轮廓。切出轮廓与切入轮廓符合轴对称关系，所以刀具Φd由P1到P2铣削圆心为O圆弧轮廓ΦD，形成铣削原理轮廓，如图4所示。

图4 铣削原理轮廓

因图形对称，选取右侧进行分析，建立数学模型。对称中线交K处水平线于T，A处竖直线交水平线TK于N，延长OA、TK交于P，如图5所示。其中，轮廓半径为R，刀具半径为r，轮廓开口距离为TK，有

图5 数学模型几何

设TK为x，有

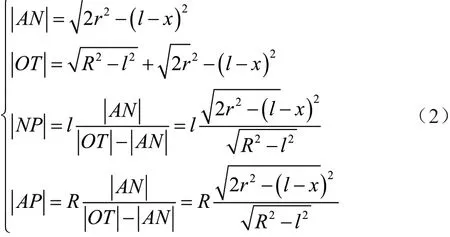
在直角△KPO1中应用勾股定理，得到

求解得到

为了刀具能完成刀补过程，必须x≥0，得到

因刀具半径必须小于孔半径，得到

式中：r为有效铣刀半径；R为圆弧轮廓半径；l为圆弧轮廓半开口宽度。

式（6）在圆弧轮廓圆心在轮廓线内侧有效。当圆弧轮廓圆心在轮廓线上时，式（6）同样实用。当圆弧轮廓圆心在轮廓线外侧时，式（6）失去意义。

3 实验验证

依照式（6），将参数R=10和l=9.7代入验证，得到rmax=7.996，最大刀具直径为15.992 mm，如图6所示。

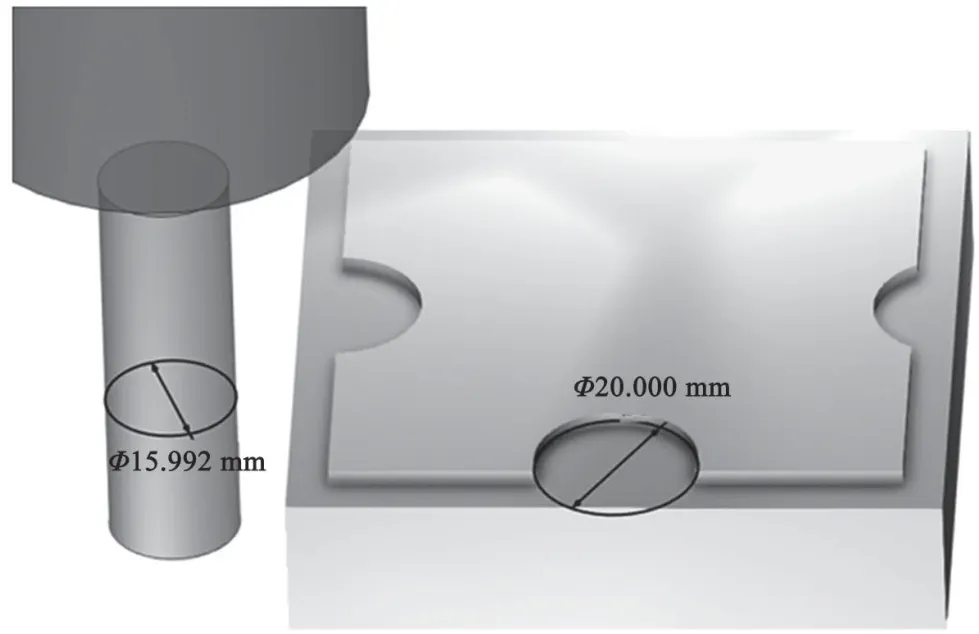
图6 最大刀具验证

为了便于说明问题，将刀具半径增加0.001 mm进一步验证，结果如图7所示，未出现Φ20 mm圆弧轮廓加工，刀具偏置失败。

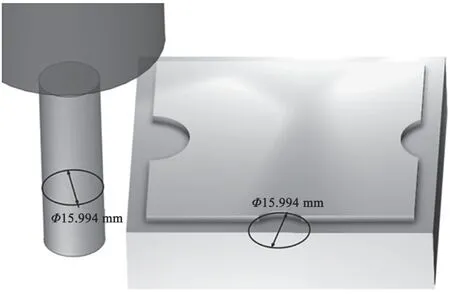
图7 超出最大刀具验证

4 结语

在轮廓铣削加工过程中，运用刀补编程并选择最大刀具半径是有效的工作方法，能极大提高工作效率，保证工作质量，降低加工成本。针对圆弧轮廓加工提出了最大刀具半径计算数学模型，并推导了计算公式。经过西门子840D系统仿真验证，最大刀具半径计算结果符合预期，并有力解决了过大半径刀具无法获得圆弧轮廓加工刀路的问题，说明最大刀具半径计算公式正确有效。