基于高斯受限玻尔兹曼机的工业产品质量智能异常检测

黄 聪，农英雄，张 毅

(1.广西中烟信息中心，广西 南宁 530001；2.清华大学 自动化系，北京 100018)

工业4.0时代，制造过程具有生产工艺复杂、成本管控精细、产品质量严格等特点，通过技术手段确保并有效提升产品良率具有重要意义且需求迫切。产品质量检测是对产品或生产过程的一个或多个特征进行测量、检验、试验或估计，并将结果与工艺要求进行比较[1]。质量检测的特征参数由生产线上配备的传感器或专门定制的检测装置测量得到。传统上，质量检测的标准主要依赖于以往经验所制定的规则。但是，现代工业产品多样化，生产工艺更新较快，而且生产过程数据容易受到生产环境的影响，规则的准确度均会大幅降低。另外，当数据空间快速增长时，很难通过确定的规则对产品质量进行描述。

随着物理计算传感技术以及人工智能技术的飞速发展，基于机器学习的智能异常检测技术应运而生，由于其在应对复杂工艺过程具有大大超越传统方法的独特优势，得到学界和产业界的普遍关注，发展迅猛[2-4]。产品质量的智能异常检测成为确保产品高质量稳产出的重要保障手段，是工业智能运维服务的重要环节之一。

无监督智能异常检测技术的原理是获取正常产品特征数据的分布范围，一旦测量数据超过正常分布范围，则视为异常数据。目前，用于解决无监督异常检测问题的机器学习方法主要有单类支持向量机(one-class support vector machine,OCSVM)[5]、局部异常因子(local outlier factor,LOF)[6]、独立森林(isolation forest,IF)[7]等，这些方法虽然具有一定的稳健性并已取得一些较好的应用，但是在应对大规模数据时，计算复杂度会大幅提高，尤其是在线检测时异常检测性能退化严重，并且扩展性较差[8]。

深度学习方法在高维大规模数据的非线性建模方面具有显著优势。受限玻尔兹曼机(restricted Boltzmann machine,RBM) 模型是一种无向二分图的神经网络模型，相对于深层神经网络模型，能够以较少的计算消耗表征数据复杂关系。RBM不仅可以作为一个生成模型，基于隐变量对一组输入变量的联合分布进行建模，还可以作为判别模型实施无监督分类[9-10]。

考虑到实际工业生产中产品参数的高斯特性，本文选取高斯RBM(GRBM) 用于建模，即可见层各神经元是服从高斯分布的。与传统基于GRBM异常检测方法不同，本文研究聚焦用于描述网络状态的自由能量函数。文献[11]与[12]同样使用能量函数值作为异常控制标准，但对自由能量函数的研究仅限于此，且应用领域与本文不同。本文将自由能量函数整合到目标函数中。在不同的阶段进行不同的梯度补偿，使训练过程易于处理。本文将FE-GRBM与3种常用的异常检测方法OCSVM、LOF、IF以及两种分别以重建误差和能量得分为决策准则的常规GRBM模型，在卷烟产品检测的实际应用案例中进行比较分析，验证FE-GRBM的有效性和优越性。

1 受限玻尔兹曼机

1.1 基本模型

受限玻尔兹曼机(restricted Boltzmann machine,RBM) 是一种可用随机神经网络(stochastic neural network,SNN) 解释的概率图模型(probabilistic graphical model,PGM) 。它由Smolensky于1986年在玻尔兹曼机(BM) 的基础上提出。RBM采用两层网络来描述一组随机变量之间的依赖关系，一层为隐藏层，另一层为可见层。相较于BM，RBM的层与层之间相互连接，但同一层内各神经元间没有连接。RBM 具有如下性质。

性质1当给定可见层各单元状态时，隐藏层各单元的激活条件独立；反之当给定隐藏层各单元的状态时，可见层各单元的激活也条件独立。

RBM的网络结构如图1所示，n、m分别表示可见层和隐藏层神经元个数。可见层状态向量x=(x1,x2,···,xn)与隐藏层状态向量h=(h1,h2,···,hm)相连接。a=(a1,a2,···,an)表示可见层的偏置向量，其中，ai是可见层第i个神经元的偏置。b=(b1,b2,···,bm)表示隐藏层的偏置向量，其中，bj是可见层第j个神经元的偏置。W=(wij∈Rm*n)表示可见层与隐藏层各神经元之间的权重矩阵，其中，wij是可见层第i个神经元和隐藏层第j个神经元的连接权重。

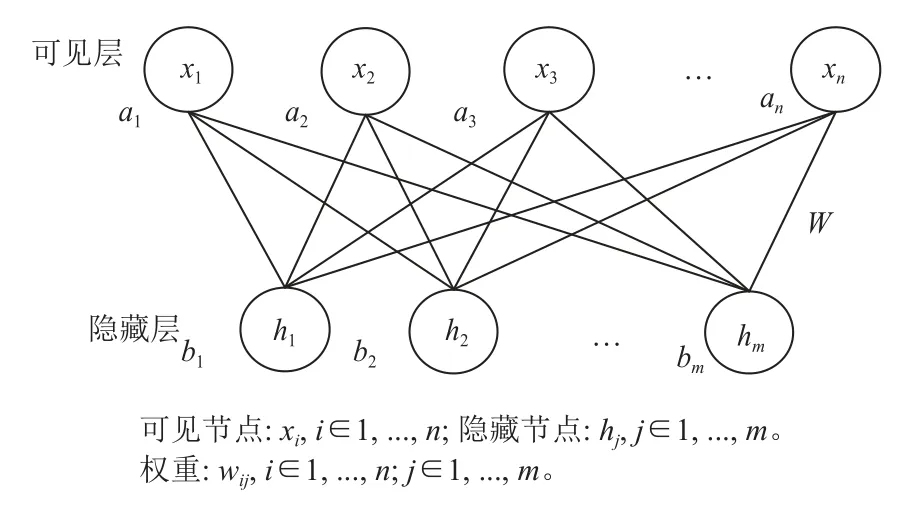
图1 RBM模型结构图Figure 1 The RBM Model structure diagram

RBM模型是一个基于能量的模型(energy based model,EBM)，对于一组给定的状态(x,h)能量函数定义为

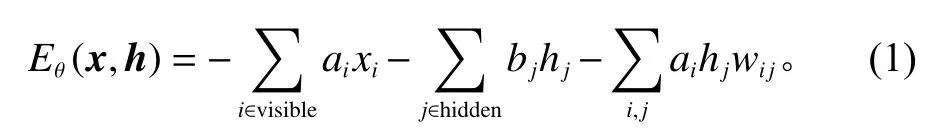
根据能量函数，可以得到关于状态的(x,h)联合概率分布为

为归一化因子，又称为配分函数(partition function) 。对于一个实际问题，更关心关于观测数据x的概率分布Pθ(x)，即Pθ(x,h)的边缘分布，也称为似然函数(likelihood function)，通过对所有可能的隐藏层状态向量求和得到

类似地，关于隐藏层状态向量h的概率分布Pθ(h)的似然函数定义为

给定训练数据后，训练一个RBM意味着调整参数θ，以拟合给定的训练样本，使得该参数下RBM表示的概率分布尽可能地与训练数据相符合。假定训练数据X=(x1,x2,···,xl)，l为训练数据数量，各数据满足独立同分布。这样，训练RBM的目标为最大化似然。为了简化计算，对似然的最大化等价于对似然对数的最大化。

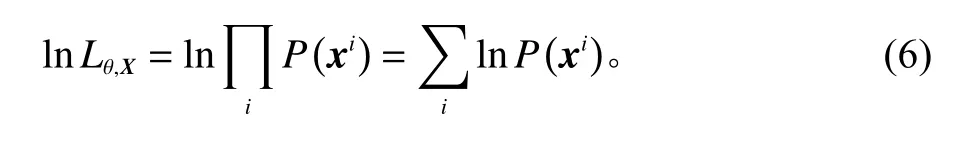
采用梯度上升法最大化式(6)，通过迭代的方式逼近最大值，迭代公式为

其中，η＞0为学习率。

由于式(3) 计算复杂度大，很难直接求得，对比散度(contrastive divergence,CD)[13]一般被用于训练。CD算法执行k次吉布斯采样，其具体步骤如下。对∀x∈X，取初始值x(0):=X，经过k步吉布斯采样生成样本x(k)。其中，第s步(s=1,2,···,k) 先后执行从P(h|x(s-1))采样出h(s-1)及从P(x|h(s-1))采样出x(s)。利用k步吉布斯采样后得到的x(k)近似计算梯度如下。

一般设置k为1，即只进行一次吉布斯采样，就能达到较好的拟合效果[14]。

1.2 变种模型

传统的RBM假设x∈{0,1}，h∈{0,1},这种情况下RBM又称为伯努利-伯努利RBM(Bernoulli -Bernoulli RBM,BRBM) 。相关公式如下。

BRBM假设每个可见层神经元和隐藏层神经元的状态都是二进制的，而现实世界中很多数据参数的取值范围都是不固定的且分布各异，这就大大限制了BRBM的应用。虽然也可以通过一些方法改进实现BRBM对其他分布的建模，但是效果较差。为了更好地对连续分布建模，提出通过修改能量函数的模型改进，使用高斯可见层神经元替代伯努利可见层神经元，即高斯-伯努利RBM(Gaussian-Bernoulli RBM,GRBM)[15]。GRBM的能量函数定义为

其中，σi定义为第i个可见单元高斯噪音的标准差。

2 方法描述

本文提出一种基于自由能量函数的GRBM故障检测方法，即自由能量函数GRBM(free energy GRBM,FE-GRBM) 。该方法采用GRBM作为数据模型框架，利用自由能量与边缘概率自然对数的线性关系，提出基于能量分值的模型训练策略和故障检测方案。

2.1 训练方法

模型的训练算法一般通过参数的对数似然函数(log-likelihood,LL)(式(6)) 最大化实现参数更新。但是由于配分函数计算复杂度大，很难直接在训练时计算得到，采用CD算法作为训练算法执行梯度上升操作。CD算法利用k(一般取k=1) 步吉布斯采样近似计算梯度，而重构误差被直接用于训练的性能度量。重构误差为吉布斯采样生成样本与原始训练数据的均方差距离，虽然计算方便，但是对模型训练而言是一种非常差的度量[16]。

GRBM模型中，每个可见层神经元都服从高斯分布。可见层神经元的边界分布P(x)是每一个可见层神经元的联合概率密度。每个神经元的高斯程度可以使用边界分布来表示。数据的联合概率密度越高则每个神经元的概率越高，数据更有可能正常。相反，联合概率密度越低，数据更可能异常，即异常程度与P(x)成反比。

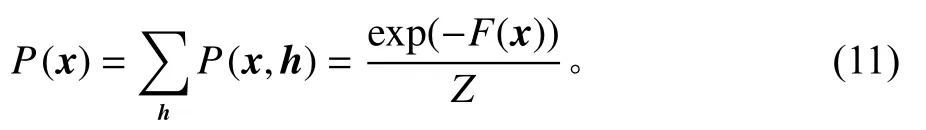
其中，F是自由能量函数。

由于配分函数(式(3)) 不可计算，可见层神经元的边界分布也很难得到。但是每个数据的配分函数值相等。可以通过抵消配分函数，并对P(x) 求对数，得到式(13) 。同时，由于异常程度是与P(x)成反比的，因此可以使用自由能量值作为数据分类的决策指标。

为了简化计算，设置可见层神经元的边缘分布方差为1，得到

将自由能量作为模型学习的目标函数，得到新的对数似然函数为

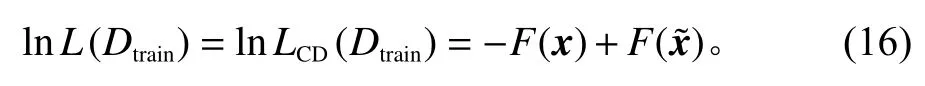
其中，x是原始数据；是重构数据。

根据式(15) 得到梯度如下。

2.2 异常检测

在线检测阶段，需要建立一个监控统计量对新进数据进行实时检测。最直接的方法是采用SPE统计量作为监控指标，当重构误差超过检测控制限后，即可视为故障数据。但是这个检测控制限难于确定，因为虽然原始数据及其重构数据遵循多元高斯分布，但它们之间是相互依赖的，两个相互依赖的多元高斯分布之间的差异不一定是高斯分布。因此，直接选用SPE统计量作为监控指标是不合适的。

2.1 节分析确定了自由能量与边缘分布自然对数的负线性关系，考虑到故障检测主要目标是进行正确的判别，尤其是有效识别出真正的故障，而不是非要构建一个精确的数据模型，因此可以将-F(x)作为监控统计量。新进数据的自由能量可以直接通过式(15) 计算得到，式中的ai、bj及wij皆可在离线建模阶段求得。另外，可见层神经元通过标准化后服从标准高斯分布且相互独立，独立高斯分布的积仍是高斯分布，那么可见层神经元的边缘分布P(x)也服从标准高斯分布。

根据式(13)，得到

可以看到，F(x)与x2是成正比关系的，而x服从标准正态分布，则x2服从标准正态分布，相应地，x也应服从标准正态分布。因此，本文采用高斯核密度估计技术(kernel density estimation,KDE) 来确定F(x)统计量的控制限。

KDE通过非参数方式估计随机变量概率密度函数[17]。概率密度函数(probability density function,PDF) 的基本估算公式为

其中，xi是观测数据点；t是窗口宽度；n是观测值数量；K是核函数。核函数满足

核函数有几种类型，如高斯核、不平滑核和余弦核等。考虑到F(x)统计量的高斯分布特征，选用高斯核函数。高斯核函数的数学形式为

另一个关键问题是需要提前明确窗口宽度t。通常通过平均积分平方误差(mean integrated squared error,MISE) 计算得到

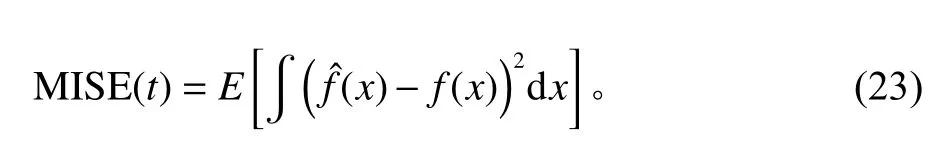
首先，计算正常训练数据的-F(x)值。其次，使用KDE估计-F(x)统计量的PDF。最后，通过逆累积分布函数(inverse cumulative distribution function，ICDF) 求得PDF的相应分位数，并将其作为置信限，当新进数据的-F(x)统计值小于控制限，则为故障数据。

2.3 算法实现

FE-GRBM方法的整体流程见算法1。整个数据集包括训练集、验证集及测试集需要首先经过统一的预处理实现度量一致。

数据预处理采用零相位成分分析(zero-phase component analysis,ZCA) 白化技术。该技术(式(24))源于PCA，区别在于没有减少原始数据的维度。

其中，xi是原输入向量；x(PCA)是对x进行PCA处理；λi是第i个特征值；ε是一个很小的常量用于避免公式分母为0，通常设置为10-5。ZCA模型是通过正常数据训练特征向量ui和特征值λi计算得到的。所有的原始数据都需要通过ZCA模型预处理，以得到最小相关度且具有相同方差的一组特征量。

模型初始需要对超参数Γ进行初始化，包括W、b、a、动量标量m、小批次样本量、隐单元数、学习率及稀疏度等。这些超参在训练过程不是固定值，而是在一个值域中波动。通常，调节前5个参数就足够了。在每个迭代周期结束，通过计算验证集的分类性能度量，取最高值的相应参数值。

整个FE-GRBM异常检测框架如图2所示。离线建模阶段通过正常历史数据建立ZCA数据预处理模型及GRBM模型，并使用KDE方法求解确定-F(x) 的控制限。在线检测阶段，新进数据首先通过ZCA模型进行白化预处理，然后根据GRBM模型计算求得监控统计量-F(x) 值，将该值与控制限比较，若小于控制限则该样本为异常样本，否则继续检测下一个样本。

图2 FE-GRBM异常检测框架Figure 2 The framework of FE-GRBM

3 烟支成品异常检测

烟支成品检测是卷烟质量检验的一个重要组成部分[18]。本文对广西南宁卷烟厂烟支成品实际检测数据开展案例分析，验证FE-GRBM的应用效果。广西南宁卷烟厂烟支成品重要物理指标的检测数据是由烟支/滤棒综合测试台采集得到的。本案例所使用的数据集由22 640个烟支检测实例组成，每个实例包含6个参数，分别为重量、圆周、吸入阻力、通风度、硬度和长度。这些实例的质量异常情况均是结合专家根据自己的经验和知识进行综合感官验证后得到的标注，其中66个实例为异常样本，占总样本的不到0.3%。

实验将FE-GRBM与3个通用的异常检测方法OCSVM、IF和LOF性能比较，用于验证FE-GRBM在无监督分类方面的优越性。另外，还将FE-GRBM与传统GRBM、采用重构误差作为监控统计量的RE-GRBM方法比较，用于验证基于自由能量的学习和监控策略的优势和必要性。所有用于比较的方法均直接利用scikit-learn工具箱编程[19]实现，各方法的超参数则通过交叉验证与网格搜索相结合的方法选择最优值。表1中列出了所有比较方法主要超参数的搜索空间。实验所有的结果都是用50个独立实验的测试平均值计算得到的。

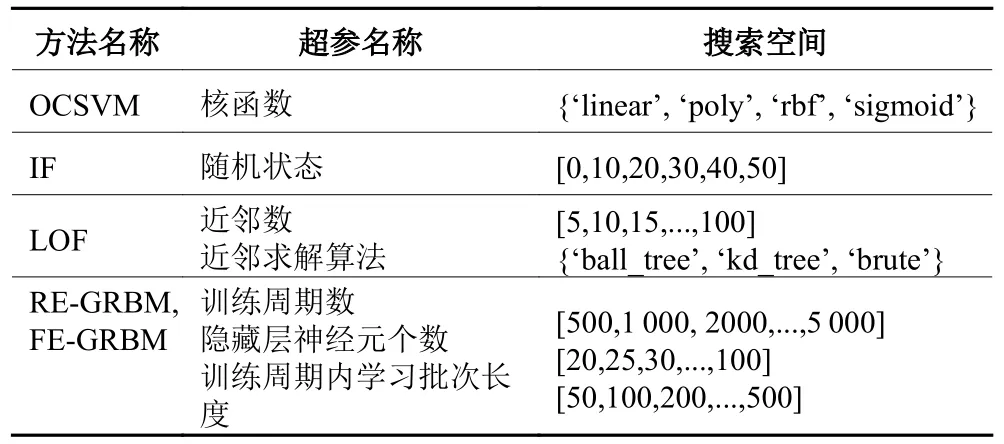
表1 实验比较方法主要超参的搜索空间Table 1 The search-space list of the main super-parameters from the comparison methods

分类方法性能通过受试者工作特征曲线下面积(receiver operating characteristic-area under curve,ROC-AUC) 和平均精度(average precision,AP) 作为评价指标。实验采取交叉验证方法开展。随机选取80%的正常样本用于训练，80%的异常样本以及相等数量的正常数据用于测试，剩下的正常数据以及20%的异常样本用于验证。所有的数据集包括训练集、验证集及测试集均需统一的标准化预处理。OCSVM、LOF和IF实施标准化预处理。其他方法使用ZCA白化预处理。在OCSVM，选择rbf为核函数，通过调节核系数来选择最好的结果。在LOF和IF中，异常点比例设置为0.05。

实验首先采用热力图技术对正常数据的相关性进行分析，图3为正常数据6个变量的相关系数热力图。可以看到，变量间具有显著的线性不相关性。

图3 正常数据变量相关系数热力图Figure 3 The heat map of correlation coefficient of normal data

实验中，FE-GRBM的隐藏层神经元个数设置为20。为了避免权重爆炸，设定学习率为0.000 5，动量参数设置为0.95，以提高学习速度。总周期数为1 000，每个学习周期设置学习样本个数为200。在建立好GRBM模型后，分别计算每个正常样本点的-F(x) 统计量。然后使用KDE来确定-F(x) 统计量的上限作为监控限。图4为通过KDE方法确定控制限的效果展示。图中虚线与x轴的交点是PDF的5%分位点，作为-F(x) 统计量的监控限。当新进样本点xi的统计值-F(x) 小于监控限时，则被检测为异常样本。

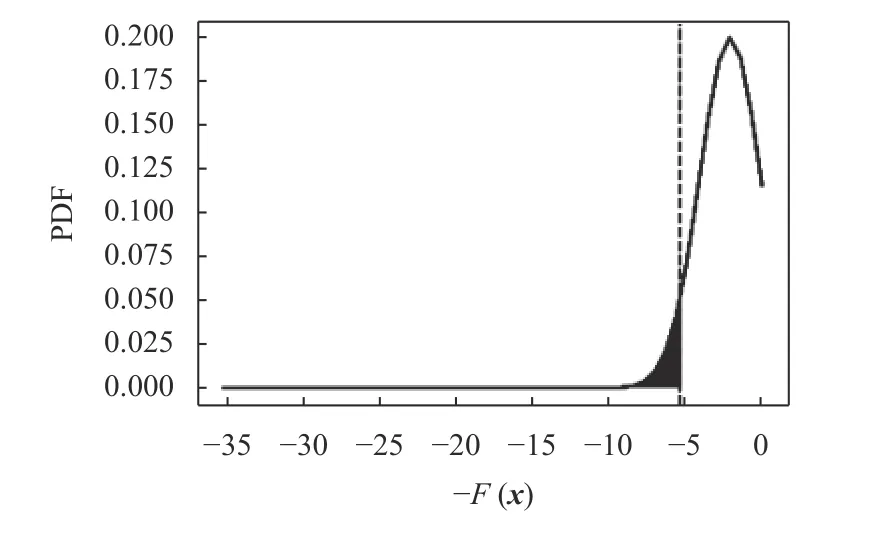
图4 KDE方法效果展示Figure 4 The illustration of KDE

实验结果见图5和表2。在ROC-AUC空间，ROC-AUC得分表示ROC曲线下的面积，而ROC曲线通过计算5种异常检测方法在不同阈值下的异常预测假阳性率和真阳性率(见式(25)) 的对应情况来反映检测效果。式(25) 中，TP是真质量异常样本数；TN是真质量正常样本数；FP是假质量异常样本数；FN是假质量正常样本数。因此，ROC-AUC得分是对异常检测效果的无差别评估，不偏向于多数类或少数类。比较5种方法的ROC-AUC得分，LOF表现最差，IF其次，OCSVM、RE-GRBM与FE-GRBM均表现很好，取得了最高分值。

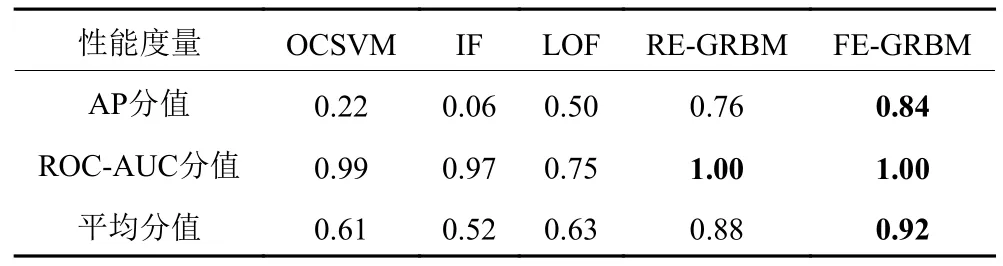
表2 实验比较结果Table 2 The experimental comparison results

图5 实验比较结果散点图Figure 5 The scatter diagram of experimental comparison results

在PR空间，AP得分(式(26)) 是对PR曲线(precision-recall,PR) 精准率取均值。式中，Pn和Rn分别是第n个阈值的精准率和召回率。AP得分展示了5种异常检测方法在不同概率阈值条件下精准率与召回率的配对。精准率和召回率(式(27)) 都是在不考虑假质量正常样本的情况下计算得到的真质量异常样本数量的指标。因此，AP分值更关注于少数类，是一个针对非平衡分类问题的有效评估指标。比较5种方法的AP得分，传统方法OCSVM、IF和LOF均表现很差，LOF得到了最高分0.50，基于GRBM的方法明显高于传统方法，其中FE-GRBM取得最高分值0.84，比LOF高出0.34。这表明OCSVM、IF和LOF针对异常样本的漏检率很高，而FE-GRBM检测出异常样本的效果最好。

很显然，基于GRBM的方法比其他3种经典异常检测方法(OCSVM、IF和LOF) 在高非线性异常检测方面具有较大的优势，FE-GRBM在本实验5种方法中体现了绝对的优势。3个经典异常检测方法平均性能得分最高是LOF，为0.63，FE-GRBM高于LOF，为0.92。这说明OCSVM、IF和LOF在处理高非线性多维度异常检测问题方面具有劣势，基于GRBM的方法能够很好地解决这个问题。FE-GRBM平均得分高于RE-GRBM 0.04，这验证了使用基于自由能量函数的学习策略和监控策略的优越性。

4 结论

本文针对传统多元统计分析方法在处理非平衡非线性异常检测问题上的缺陷，利用浅层深度神经网络在非线性建模和算法复杂性上的综合优势，提出基于自由能量高斯玻尔兹曼机的故障检测方法FE-GRBM。利用自由能量函数与概率密度函数的反向线性关系，设计基于自由能量函数的学习策略，有效解决使用重构误差训练效果差的问题；并在此基础上提出改进的监控策略。通过烟支成品异常检测的实际工业案例，验证FE-GRBM的优越性。下一步将继续对不同的实际工业应用场景进行应用研究。