锂离子电池储能系统多时间尺度均衡方法

丁 凯，钱一民，陈 乔，郑 剑，王 易

（国网湖北省电力有限公司电力科学研究院，湖北 武汉 430077）

后备电源在系统发生故障时，能够保障核心设备的正常工作[1-2]。相比于阀控密闭铅酸电池，锂离子电池(以下简称“锂电池”)因能量密度高、无记忆性、低自放电率、绿色环保等优势被广泛应用于电力直流电源系统[3]。后备电源的传统技术方案是将多节电池串联成组后并入直流母线[4-6]，如图1(a)所示。该技术方案最为明显的缺点是：若单节电池损坏，后备系统将直接故障。对于高压故障，如无法提供后备操作电源，将导致本级断路器无法分闸，甚至直接使上级电网跳闸。另外，由于电池单体电压一般在4 V左右，为了满足直流系统高电压的需求，需要将几十甚至上百节单体串联。而串联电池越多，各电池单体之间的均衡就越复杂。所以，针对上述传统技术方案的缺点，出现了先串联电池后并联模组的并联型备用电源方案[7]，并联型方案如图1(b)所示。即先将性能相对一致的电池串联成组，再为各串联电池组配备独立的DC-DC 转换器并联后为负载供电。以这种并联模组代替后备电源传统的串联模式，不仅避免了因某块电池单体故障导致整个串联电池组无法使用的木桶效应，并且并联模组之间能够互为备用，显著提高了后备电源的可靠性与能量利用率。

图1 后备电源串、并联模式比较Fig.1 Comparison of series and parallel of back-up power supply

电池的内阻、自放电率等特性都会有微小差异[8]，具体表现为，串联电池组会出现单体电压分布不一致的现象，若不能及时均衡，可能引起特定电池单体过充、过放甚至是爆炸等危险[9-11]。而并联电池组则直接表现为电流分布不一致，这将导致电池能量分布与容量衰减差异[12-13]。并联电池模组不同的容量衰减，会使某些模组提前到达截止寿命，破坏了多个并联模组之间互为备份的关系，降低了系统整体的可靠性，且需要额外的人力去检查，增加系统的维护成本。故需要对先串后并的并联型方案进行寿命均衡处理，使各电池单体的特性尽量接近。

对串联电池组均衡方法的研究有很多[14-25]，主要分为被动均衡和主动均衡两大类。被动均衡[14-16]主要依靠耗能型元件(如电阻)消耗电池组中能量较高电池单体的多余能量，使电池组的能量保持一致。被动均衡方法在均衡过程中会产生大量热能，如果散热处理不当，易导致电池系统热失控，且被动均衡并不能最大化利用电池组的能量。

主动均衡[17-25]分为旁路均衡以及基于能量转移的均衡。基于能量转移的均衡[17-22]主要是由电容、电感、变压器等储能元件构造额外的能量传输通道，再设计相应的管理策略，将能量较高单体中的多余能量转移到能量较低的单体。基于能量转移的均衡主要分为4种：单体-单体(cell-to-cell，C2C)、单体-电池组(cell-to-pack，C2P)、电池组-单体(pack-to-cell，P2C)、单体-电池组-单体(cell-topack-to-cell，C2P2C)。相比于被动均衡，基于能量转移的均衡方法具有能量利用率高、均衡速度快、电池组一致性好等优点。但是，该方法也存在如拓扑体积大、成本高、控制算法复杂等问题。旁路均衡方法[23-25]主要利用可控开关阵列调整能量流动的路径，通过设计相应的控制策略去控制开关阵列的开通、关断就能改变能量流动路径。最简单的控制策略是在电池组充电时旁路能量较高的电池单体，在电池组放电时旁路能量较低的电池单体。此方式下电池能量直接流向负载，不需要在不同电池单体之间转移，这就使电池的能量不会在转移过程中被消耗，提高了电池能量的利用率。同时，通过改变开关阵列也能够适时旁路故障单体。相比于基于能量转移的均衡方法，旁路均衡方法不仅均衡速度快而且均衡拓扑结构简单、成本低、容错率高、能量利用率高。

电池组均衡的指标有开路电压(open circuit voltage，OCV)、电池端电压、荷电状态(state of charge，SOC)三种。OCV需要电池静置较长时间到达电池内部平衡后才能测得，并不适合用作均衡指标。多数均衡策略都使用端电压以及SOC 作为均衡指标[26-30]。其中，SOC定义为电池剩余的可用容量占当前容量的比例，保持电池SOC 的一致性是均衡的根本目的。虽然端电压也能间接反映电池的SOC，但是电压与SOC 变化的非线性关系可知端电压难以精确反映电池的SOC[31]。

并联电池组的均衡电路需要与电池/电池组隔离，常用的均衡拓扑结构为每个电池模组配备独立的DC-DC 转换器，使得每组电池的充/放电量可以独立控制。Moo等[32]通过为并联电池组中的每块电池单体配备DC-DC 转换器独立控制每块电池的电流。该方法不仅能够避免电池组过充放，同时也有利于电池组工作过程的SOC、SOH(state of health，健康状态)估计。Cao等[33]提出了一种多输入单输出的电池系统，即为每组电池模块配备独立的DCDC 转换器后将所有模组串联为负载供电。该系统不仅能够使并联电池组达到SOC 均衡，也能在文献[32]所提均衡拓扑基础上减少电池系统所需的元件数。Ur Rehman 等[34]则为每块电池配备独立的DC-DC 转换器后，设计算法增加高SOH 电池的放电深度，以提高电池衰减的一致性、延长电池组的整体寿命。

为此，对于上述并联方案现有的电池不一致性问题，本文提出了一种针对后备电源的锂电池储能系统多时间尺度均衡方法，同时兼顾电池组组内SOC 均衡与电池组组间寿命均衡。即在电池模组组内进行旁路均衡使电池组在短时间尺度实现SOC 均衡，在并联电池模组组间进行长时间尺度寿命均衡。若使用本文所提的均衡方法使得各并联电池模组同时达到截止寿命，就可以一次性完成电池更换等工作，也能够确保并联型电池系统在作为备用电源期间各个模组的互为备份作用。所提的多时间尺度均衡方法不仅提高了锂离子电池的利用率，也能确保备用电源的可靠性。

1 系统均衡拓扑结构

本文所提的多时间尺度旁路均衡采用如图2所示的拓扑结构。

图2 储能系统拓扑结构Fig.2 Topology of energy storage system

图2所示并联电池模组的拓扑结构能够根据负载需求调整输出端电压以及电流，也可以根据电池模组的性能独立调节各电池模组的电流。电池模组内部串联电池组的旁路均衡拓扑可以通过开通/关断开关，旁路任意电池单体，以此实现电池组组内单体SOC均衡。以电池模组内部串联电池组的3块不同SOC 的电池单体为例。若电池组处于放电状态，则开通开关①②④，关断其余开关，旁路能量最少的电池单体。若电池组处于充电状态，则开通开关①③⑤旁路能量最高的电池单体。采用图2所示模组并联的模式，若此时模组2出现故障，则通过DC-DC转换器调控使其输出功率为0，而其余电池模组仍然正常工作使得系统依然能正常运转。若采用传统的串联技术，模组2出现故障时，整个系统都会停止工作。所以，这不仅避免了串联电池组固有的木桶效应，又能使不同并联电池模组之间互为备用，显著提高直流系统的安全性、可靠性。另外，对于各并联电池模组而言，可以提前将电池单体按照性能一致性分组，降低串联电池组组内SOC 均衡的难度，加快组内SOC 均衡的速度为下一步模组之间寿命均衡提供有利的时间条件。

2 均衡算法

本文所提对串并联电池组的多时间尺度均衡方法：在短时间尺度内，使串联电池组组内SOC 在短时间内快速达到均衡；在长时间尺度上，根据并联电池模组的老化程度调节其充放电深度，以此实现寿命均衡。图3描述了均衡算法中长短时间尺度均衡如何协调：当串联电池组组内SOC 在短时间快速达到均衡后就可以启动长时间尺度寿命均衡。

图3 长短时间尺度相互配合的算法流程Fig.3 Flowchart of the algorithm for interfacing long and short time scales

2.1 基于功率加权的长时间尺度寿命均衡控制算法

并联电池模组寿命均衡的本质是根据各模组的健康状态控制电池的放电深度，整体原则为：剩余寿命越少，则该组电池模组的放电深度越浅；剩余寿命越多，则该组电池模组的放电深度越深。结合本文的拓扑结构，利用DC-DC 转换器调控各电池模组的发出功率，就可以达到控制模组放电深度的目的。故根据上述原理，本文提出了基于功率加权的寿命均衡控制算法，如图4所示：首先计算各电池模组应该提供的补偿SOC；然后将各电池模组的容量除以参考容量，得到关于荷电量的权重因数，并利用该因数去修正各电池模组的SOC(即归一化)。最后，再将各电池模组的SOC 除以各电池模组SOC 之和，得到关于功率的权重因数，并根据该因数和补偿SOC 得到各电池模组需要提供的实际功率。算法的具体内容如下：

图4 长时间尺度寿命均衡控制算法流程Fig.4 Long time scale life balance control algorithm flow chart

当串联电池组在短时间内达到SOC 均衡后，取电池组SOC的平均值为各模组(假设模组数目为N)的SOC(SOCave1，SOCave2，…，SOCaveN)，平均容量为各模组的容量(Q1～QN)，假设容量大小关系为Qmax=Q1>Q2…>QN=Qmin。为了实现各并联电池模组之间的寿命均衡，可以计算出各模组相对于健康状态最差电池模组应额外提供的补偿SOC(∆SOC)，计算方式如式(1)

式中，k1～kN-1为比例系数，单位为1/Ah。k1～kN-1的取值并不一定相等，且取值需要根据各模组的容量差进行调节，本文取值为8～10即可达到最佳调节结果。该比例系数不仅可以将容量的单位转换为“1”，也能通过适当调整该比例系数使∆SOC更贴合模组之间的寿命差异。

如果在对并联的电池模组进行寿命均衡时，直接根据各模组当前的SOC(即SOCave1，SOCave2，…，SOCaveN)计算权重因数显然不符合实际情况。因为SOC定义为剩余可用电量与电池容量的比值，只是一个相对值。当各模组的老化程度不同时，其SOC变化对应的电量也不同。若电池组1的老化程度比电池组2的高，那么电池组1的SOC变化量所对应的电量会低于电池组2。所以，算法应该先将各模组的SOC归一化至相同水平下(可任选参考值进行归一化)，以便于进行并联电池组之间的比较与量化。假设算法选择将所有模组的SOC 以最大容量Qmax作为参考值进行归一化，则各并联模组的SOC将转化为SOC'ave1～SOC'aveN：

式中，SOC'avei为各电池模组在同一水平下的SOC。

为实现并联电池组的寿命均衡，需要让健康状态较好的电池组承担更多的功率输出，因此，可以利用各电池组归一化后的SOC以及待补偿∆SOC，综合决定各电池组应提供的瞬时功率P1～PN：

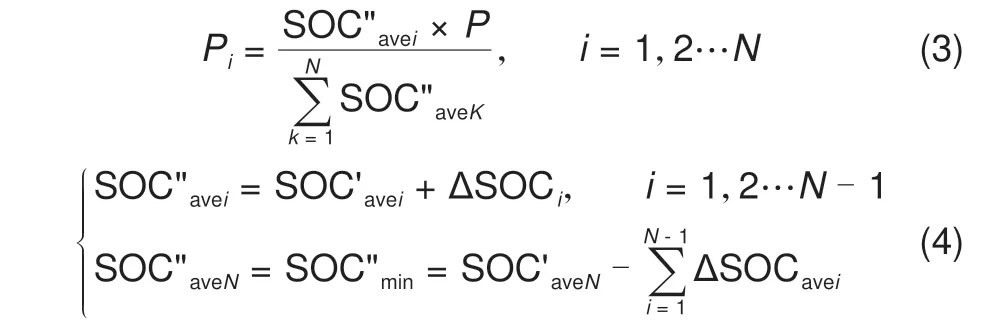
式中，P为负载所需的总功率；Pi为各并联模组应提供的输出功率。根据上述方法控制电池模组的放电深度，会使得健康状态较好的电池模组放电深度更深，健康状态不高的电池模组放电深度更浅。该方法使所有并联电池模组充放电呈现良性循环，最终使各电池模组同时达到截止寿命，减少更换电池的次数，方便运维与梯次利用。

2.2 基于SOC旁路的短时间尺度串联电池组均衡算法

串联电池组SOC旁路均衡算法的基本策略是：根据电池组SOC 值的标准差判断电池组是否需要均衡。若电池组SOC的标准差小于所设定的阈值，表示电池组SOC不需要均衡，则电池组串联运行。若电池组SOC 的标准差大于所设定的阈值，则需要对电池组进行旁路均衡。假定电池组需要旁路Nbypass块单体，判断此时电池组的充放电状态。若电池组放电，则通过控制开关阵列旁路Nbypass块能量最低的电池单体；若电池组充电，则通过控制开关阵列旁路Nbypass块能量最高的电池单体。该算法的流程如图5所示。

图5 短时间尺度SOC均衡算法流程Fig.5 Flow chart of short time scale SOC equalization algorithm

3 仿真验证

3.1 电池模型

搭建能够同时反映电、老化特性的锂电池模型，对于本文所提多时间尺度均衡策略的验证至关重要。本文的电池模型是基于混合功率脉冲特性(hybrid pulse power characterization，HPPC)循环放电实验和加速老化实验建立的一阶RC 模型，如图6所示。R0、R1、C1分别为电池的欧姆内阻、极化内阻、极化电容、Ub为电池端电压。HPPC测试的基本原理是利用一系列充放电脉冲作用于电池不同SOC 以计算不同充放电倍率下的内阻[35]，如图7(a)、(b)所示。根据脉冲电流结束后静置阶段的电池端电压变化(即t0～t1阶段)，可计算得到电池的欧姆内阻(R0)。由于电容两端的电压不能突变，静置阶段电池两端电压会呈指数变化趋势(即t1～t2阶段)，利用该段指数变化趋势，可计算得到电池的极化内阻(R1)和极化电容(C1)。同时，电池的OCV也可以在静置阶段(t1到下一个脉冲加入阶段)结束后得到。故利用该方法即可获得不同SOC 所对应的等效电路模型参数(R0、R1、C1、OCV)。具体计算方法如下[36]：

图6 锂电池一阶RC等效电路模型Fig.6 First-order RC equivalent circuit model of a battery

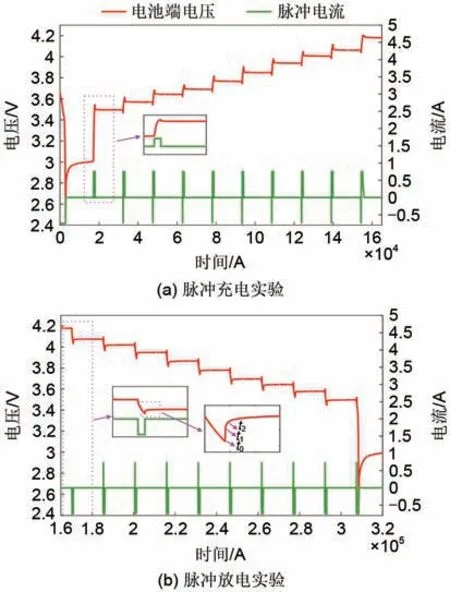
图7 HPPC工况Fig.7 The profile of HPPC

式中，tcp为电流脉冲持续的时间；Icp为电流脉冲的大小；τ为一阶RC电路的时间常数。

电池容量Qbat会随着电池老化而下降，对Qbat演变规律的建模则主要以电池容量标定值为依据。电池老化表现为电池容量的衰减，其根本原因是充放电过程中损伤的不断累积，可以通过安时数的累积量Ahthroughput反映。因此，通过分析锂电池加速老化试验的结果，即可得到Qbat与Ahthroughput的近似关系，如图8 所示。假定新电池容量为Qbat(t0)，经过充放电循环老化，该电池容量衰减为Qbat(t1)。在此过程中，电池的累积安时数为Ahthroughput_1。若继续充放电使电池容量衰减为Qbat(t2)，则可以得到由Qbat(t1)到Qbat(t2)的衰减过程中累积安时数为Ahthroughput_2。以此类推，可以获得电池容量由Qbat(t0)衰减为Qbat(tEOL)整个过程中累积安时数分别为Ahthroughput_1、Ahthroughput_2…Ahthroughput_m。实际应用中对电流累积，能够容易地获得电池的累计安时数Ahthroughput[式(9)]，因此，能够及时通过模型获得电池的当前容量Qbat。

图8 电池真实容量与累积容量随电池老化的变化过程Fig.8 The evolution of the true and cumulative capacity of a battery as it ages

通过使用插值法能够根据已知数据点获得特定区间内的未知量，以解决上述电池建模过程测量点离散的问题。为了得到对应于区间SOC∈[0%，100%]以及Ahthroughput∈[0，∞]内的未知参数，本文使用如下三阶埃尔米特插值方法：

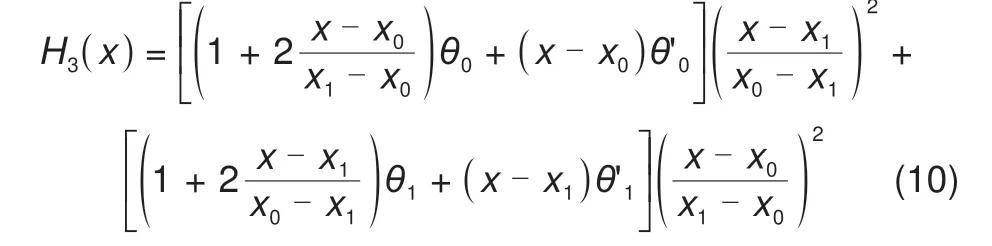
式中，[R0，R1，C1，OCV，Qbat]∈θ；[SOC，Ahthroughput]∈x；x0、x1为待插值点的相邻的两个点的位置；θ0、θ1是应于自变量x0、x1的因变量；θ'0、θ'1是对应的导数。

图9 为锂电池电-老化模型的示意图。获得电池当前容量Qbat后，根据安时积分法实时更新电池当前的SOC(如图9 中的A 部分)。又因为一阶RC模型的各个参数都与SOC 相关，故可以根据电池当前的SOC 更新等效电路模型参数(如图9 中的B部分)。

图9 锂电池电-老化模型Fig.9 Schematic diagram of Li-ion battery electric-aging model

3.2 算法验证

为了验证所提算法的效果，设计了3组对比实验，利用MATLAB/Simulink仿真平台搭建了由3组电池模组并联组成的小型储能系统，其中3个并联电池模组由6块电池单体串联组成(6S3P)，且设定恒功率负载为P=500 W。图10 为储能系统的仿真示意图，控制器中包含完整的均衡算法。控制器根据电池模组电压、SOC、容量等参数输出电池模组需要输出的功率并将该功率反馈给各电池模组。

图10 6S3P储能系统仿真Fig.10 6S3P energy storage system simulation schematic

假设6S3P 模型的3 个并联电池模组分别命名为M1、M2、M3。SOCi,j(i=1,2,3；j=1,2…6)代表模组i中的电池单体j的SOC。模组内电池单体的初始SOC分别设置为[SOCi,1, SOCi,2, SOCi,3, SOCi,4,SOCi,5, SOCi,6] = [95%, 96%, 92%, 90%, 85%,84%]，每个模组的初始容量分别设置为[M1,M2,M3]=[1.5019 Ah,1.4878 Ah,1.4637 Ah]，且各电池模组的OCV会随着模组初始容量的变化而变化。

为了验证所提均衡算法的有效性，设计了3组对比实验：

实验1：本文所提多时间尺度均衡方法[图11(a)、图12]；

实验2：仅在电池模组组内进行SOC均衡，并联电池模组之间不均衡[图11(b)、图13]；

图11 3组实验所得的各模组容量随时间变化的曲线Fig.11 Curves of capacity of each module with time obtained from three experiments

实验3：电池模组组内以及并联电池模组之间均不进行均衡[图11(c)、图14]。

图11(a)～(c)分别为3 组实验中各电池模组的容量随时间变化的曲线；图12(a)～(c)分别为实验1中各电池模组组内电池单体的SOC 随时间变化的曲线；图13和14的子图分布则与图12相同。图15分别为实验1～3中6S3P小型储能系统中每个并联模块到达截止寿命的时间。由图11(a)可知，使用本文所提均衡算法后，老化程度不同的模组可以同时达到截止寿命(即EOL_M1=EOL_M2=EOL_M3)。图11(b)、(c)显示，仅对电池模组组内使用SOC均衡以及电池模组组内、组间均不使用均衡算法并不能在长时间尺度上使各电池模组同时达到截止寿命(即EOL_M1>EOL_M2>EOL_M3)。图11 的结果表明本文所提的多时间尺度均衡算法是有效的。

由图12 可知，使用本文所提的均衡算法后，各电池模组在工作过程中其组内SOC 能够保持一致。但放电深度不同，即：健康状态最好的电池模组M1放电深度最深，老化程度最多的电池模组M3放电深度最浅，这是电池模组在长时间尺度保持寿命均衡的关键之处，也表明了所提多时间尺度均衡策略在长短时间尺度上均衡的有效性。虽然从图13可以看出在仅对电池模组组内使用SOC 均衡的条件下，各并联电池模组内电池单体SOC能够均衡。但是放电深度并没有根据并联模组的老化程度不同而有所区别。所以实验2所实现的均衡过程对实现电池模组长时间尺度的寿命均衡没有积极意义。而图14 则显示电池模组组内、组间均不使用均衡算法时，并联模组内电池的单体SOC 不仅无法保持均衡，各电池模组的放电深度几乎达到了100%。

图12 实验1的结果Fig.12 The results of experiment 1

图13 实验2的结果Fig.13 The results of experiment 2

图14 实验3的结果Fig.14 The results of experiment 3

根据图15可知，实验1中M1～M3的寿命分别为693298 s、693083 s、693084 s；实验2中M1～M3的寿命分别为684051 s、660828 s、634667 s；实验3中M1～M3的寿命分别为711607 s、687305 s、660229 s。另外，实验1中各模组的平均寿命差为143 s，最大寿命差为215 s，实验2中各模组的平均寿命差为32923 s，最大寿命差为49384 s，实验3 中各模组的平均寿命差为34252 s，最大寿命差为51378 s。故由3组实验的实验数据可知实验1中3个并联模组的寿命几乎相同，而实验2和实验3中的3 个并联模组的寿命差则非常大。对于实验2和3的情况而言，若M2和M3提前达到截止寿命时，各个并联模组之间不再具备互为备用的关系，系统可靠性降低，需要运维人员及时更换电池模块。而并联的电池模组数目越多，运维的成本也就越大。若将本文所提方法应用到实际场站，则可以在整个运行过程中始终保障备用电源系统的高可靠性，且仅需在各个模组到达截止寿命时，对备用电源进行一次运维。另外，图15中，实验1中各电池模组的平均寿命为693155 s，实验2中各电池模组的平均寿命为659849 s。故对比实验1和实验2可知，在使电池模组组内电池单体的SOC 保持一致的基础上，使用本文所提的多时间尺度均衡算法可以延长系统的平均寿命。这也间接说明仅考虑电池短时间尺度的均衡，不考虑电池长时间尺度的均衡，并不能在长时间尺度最大化利用电池的能量。

图15 3组实验所得的系统寿命Fig.15 System lifetime obtained from three sets of experiments

综合对比3组实验数据可知文章所提的均衡算法具有以下优势：①电池模组组内在电池工作的过程中可以一直保持SOC均衡，避免了电池单体出现过充或者过放等现象。②并联电池模组可以同时达到截止寿命，避免电池模组多次更换，减少运维成本。

4 结论

为解决备用电源传统串联技术方案的“木桶效应”以及并联型方案电池模组组内SOC、组间寿命等的不一致性问题，提出了一种针对并联型锂离子电池储能系统的多时间尺度均衡方法。该方法的核心思路是在电池模组组内进行旁路均衡使电池组在短时间尺度实现SOC 均衡，在并联电池模组组间进行寿命均衡，使各电池模组在长时间尺度上达到统一的截止寿命。

为了合理设计该均衡方法，根据电池工作特性设计了包含电池模组组内SOC 旁路均衡算法和基于功率加权的寿命均衡控制算法的多时间尺度均衡算法。为了验证所提均衡算法的可行性以及有效性，对锂电池进行了HPPC以及加速老化测试，然后根据试验数据，建立了锂电池电-老化模型。最后，设计了3组对比实验。实验结果显示文章所提的多时间尺度均衡算法不仅可以保持电池模组组内SOC 均衡，也能在长时间尺度上让各电池模组同时达到寿命终止，兼顾单体SOC 的一致性和电池模组寿命的一致性。这不仅解决了串联电池组的木桶效应，也减少了电池的更换次数，降低系统的运维成本。