改善风火打捆系统暂态稳定的限流式SSSC 控制策略

李娟，李方媛，王鹏，郭浩，侯宁

（1.东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 吉林 132012）

0 引言

在我国西北、东北、华北地区，风能和煤炭资源储量丰富[1]。这些地区用电负荷较轻，火力发电和风力发电又相对集中，这为实现风电、火电联合外送提供了可能。风电出力具有间歇性与波动性，远距离无法进行单独外送，通过利用“风火打捆”联合外送的输电方式可以解决风电“难送”的问题，并且该供应方式成本低、效率高。但是采取该输电方式，电网结构相对薄弱，风火打捆联合外送在带来一定经济效益的同时，相应的对电力系统的稳定运行也有一定影响[2]。

关于风火打捆暂态稳定运行的分析，许多专家学者已开展了深入的研究。文献[3]在分析风电、火电联合外送系统暂态稳定问题时，分别采用了特征值法和暂态稳定指数法。文献[4]的研究表明风电并入电网后对同步机组的暂态稳定性影响不具有一致性。文献[5]分别从无功和有功两个层面分析了风火联合外送系统中风电对系统暂态稳定性的影响。研究表明通过风电机组的无功控制可以减轻风电并网后对同步机组稳定性的不利影响，改善了系统暂态稳定性。而文献[6]通过某地风火打捆联合远距离外送的案例表明了由于风电的接入，机组间易失步，严重削弱了风火打捆系统暂态稳定性。

电力系统的暂态稳定是保障电力系统安全稳定运行的重要保障之一，所以提高风火打捆系统的暂态稳定性变得极为重要。文献[7]基于风电机组的功角快变特性，进行了风电机组的转动惯量对系统稳定性的机理分析，通过采取相应的附加控制策略，提高风火打捆系统的暂态稳定性。文献[8]根据风火打捆系统功角失稳的原因提出了风火协调切机策略解决系统突发故障，说明对于提高系统功角暂态稳定性采用火电切机策略优于采用风电的切机策略。除了上述文献中通过控制提高风火打捆系统的暂态稳定的方法外，有文献提出利用FACTS器件改善风火打捆系统的暂态稳定性。文献[9]在通过分析提高系统的阻尼特性可以提高风火系统暂态稳定性机理的基础上，采取了电力系统稳定器和静止同步串联补偿器的附加阻尼控制来改善电网系统的风火系统的暂态稳定性。文献[10]基于风火打捆系统等效外特性模型，提出利用限流式SSSC提高风火打捆系统的暂态稳定性，但该文献主要进行限流式SSSC 提高风火打捆系统暂态稳定性的机理分析，并没有考虑如何根据风速引起的风功率变化对限流式SSSC 进行控制以提高风火打捆系统暂态稳定性的问题。

本文在文献[10]的基础上通过分析风速引起的风功率变化对风机等值参数的影响，研究风功率变化对风火打捆系统暂态稳定性的影响，提出限流式静止同步串联补偿器相应的控制策略来改善风火打捆系统的暂态稳定性。

1 含限流式SSSC风火打捆系统暂态稳定型

1.1 限流式SSSC工作原理简述

含限流式SSSC 风火打捆系统见图1。图中虚线框部分为限流式SSSC，根据文献[10]，在系统正常运行状态下，限流式SSSC 的限流器部分被短接，装置等效为常规SSSC 运行，按SSSC 的原理工作。当系统发生短路故障时，在限流式SSSC 的过渡限流态时，由限流电感立即切入限制短路电流。当进入完全限流态时，串联耦合变压器的副边开路，为保证SSSC 模块不被损坏将其退出运行，此时由限流电阻RF工作。当故障切除后，限流器退出，又由SSSC 模块工作。

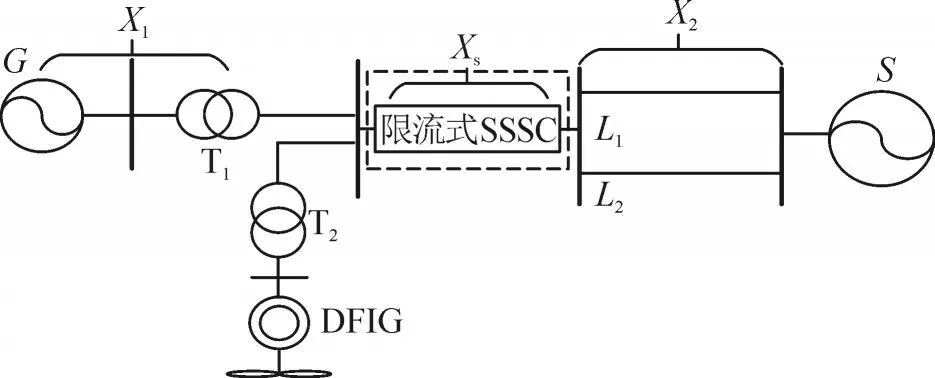
图1 加入限流式SSSC风火打捆系统图Fig.1 Diagram of adding current limiting SSSC wind-thermal binding system

1.2 含限流式SSSC风火打捆系统暂态稳定数学模型

图1 所示的系统，根据文献[11]双馈风机在正常运行状态下等值为一负电阻；在故障期间等值为一个负电阻与一个负电抗并联；在故障切除前期，DFIG 仍等值为另一负电阻与一负电抗并联，但时间较短可忽略不计；在故障切除后期其等效为一负电阻。双馈风机等值的电阻和电抗值的大小公式为

式中：Pe为风机发出的有功功率；Qe为风机发出的无功功率；us为风机机端电压。

因此，图1 所示的含限流式SSSC 的风火打捆系统在不同运行状态下的等效电路图见图2。

单端送电系统的功率特性方程[11]为

式中：为同步电机的电势；U为无穷大系统的电压；δ为与U的角度差；Z11、Z12分别为送端同步机组的自阻抗以及互阻抗；α11、α12分别为自阻抗和互阻抗相应阻抗角的余角。

由式（2）可知，风火打捆系统的功率特性由送端同步机组的自阻抗Z11、自阻抗相应阻抗角角的余角α11、互阻抗Z12和互阻抗相应阻抗角的余角α12这4 个参数所决定。由图2 等效电路（a）、（b）、（c）可分别求出风火打捆系统正常、故障、故障切除3种运行状态下的参数，见式（3）（-11）所示。

图2 风火打捆系统各运行状态下含限流式SSSC等效电路Fig.2 Equivalent circuit of current limiting SSSC in different operation states of wind-thermal binding system

1）系统正常运行时。

送端同步机组自阻抗Z11的公式为

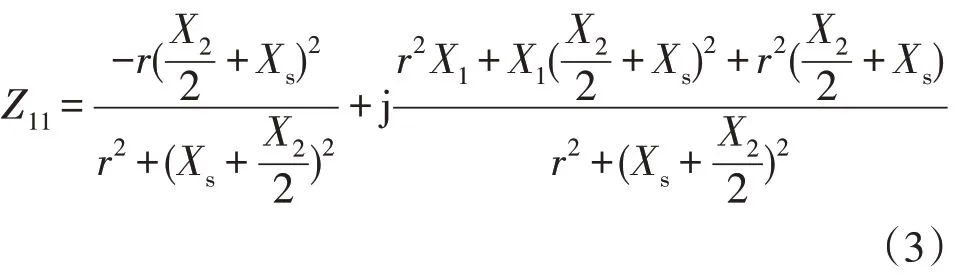
送端同步机组自阻抗的阻抗角余角α11的公式为

送端同步机组自阻抗Z12的公式为

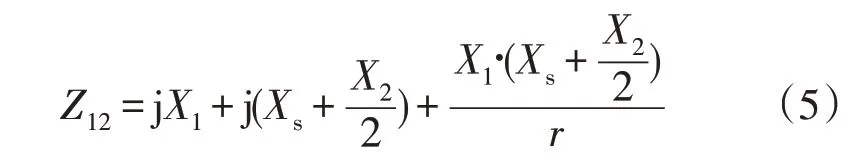
送端同步机组互阻抗的阻抗角余角α12的公式为

送端同步机组互阻抗模值|Z12|为的公式为

式中：X1为同步电机和变压器的电抗之和；X2为线路电抗；r为风电场等值参数；Xs为限流式SSSC 装置的等效电抗。

2）系统发生短路故障时。

根据文献[10]分析可知当风火打捆系统不包含SSSC 时，α11=0；|Z12|为无限大，此时发电机输出的电磁功率几乎为0，发电机转子加速，功角增大，危害系统稳定。加入限流式SSSC 后，送端同步机组互阻抗Z12公式为

互阻抗模值公式为

式中：x为风电场等值参数；RF为限流式SSSC 的等效电阻。

3）系统切除故障后。

当系统切除故障后，由于切除一条线路，线路等值电抗变为原来正常运行的2 倍，此时的送端同步机组互阻抗Z12的公式为

互阻抗模值公式为

2 基于风机等值参数分析风速对含限流式SSSC风火打捆系统暂态稳定性的影响

2.1 风机等值参数对含限流式SSSC风火打捆系统暂态稳定性影响

1）系统正常运行下的分析。

由1.2 节可知，系统正常运行时，双馈风机在正常运行时等值为负电阻。决定风火打捆功率特性的参数Z11、α11、Z12、α12都是关于风机等值电阻r的函数，将4 个参数代入式（2），可得风火打捆系统的功率极限与风机等值电阻r的关系。根据静态安全约束、潮流收敛约束、外部电网注入功率约束及暂态稳定校验约束条件，计算系统风电极限接入容量[12]。通过风电极限接入容量计算此时的风电场等值电阻为0.064 p.u.，即r的最小值为0.064 p.u.。系统的功率极限随r的变化曲线见图3。

图3 风电场等效电阻与系统功率极限关系Fig.3 Relationship between equivalent resistance and system power limit of wind farm

由图3 可以看出，风火打捆系统的功率极限随着风电机组等值电阻r的增大而增大，而系统功率极限提高，有利于改善风火打捆系统的暂态稳定性。

2）系统故障下的分析。

由1.2 中式（8）可知，加入限流式SSSC 后风火打捆系统端同步机组互阻抗模值为风机等值参数r与x的函数，为了方便分析风机等值参数r和x与系统功率极限的关系，分别固定参数r和x，研究另一个参数的变化对功率极限的影响。由式（2）和（8）可得系统功率极限与风机等值参数r与x的关系见图4。

图4 风电场等效电阻、等效电抗与系统功率极限关系Fig.4 Relationship among equivalent resistance，equivalent reactance and system power limit of wind farm

由图4 可以看出，当风机等值的参数r与x减小时，系统的功率极限皆随之增大，有利于提升风火打捆系统的功率传输能力，提高系统的暂态稳定性。

3）系统故障切除后的分析。

由1.2 节可知，系统故障切除后，由于切除了一条线路，线路等值电抗为原来正常运行的2 倍，此时的送端同步机组互阻抗模值如式（11）所示，系统故障切除后，风电场又等效为一电阻，其分析原理与系统正常运行时相同。当风机的等值电阻r增大时，系统的功率极限提高，系统的传输功率增大，进而提高了风火打捆系统的暂态稳定性。

2.2 基于风机等值参数分析风速对含限流式SSSC风火打捆系统暂态稳定性的影响

基于2.1 节中风机等值参数对风火打捆系统暂态稳定性影响的分析，接下来通过分析系统在不同运行状态下风速变化对风机等值参数的影响，进而说明风速对风火打捆系统暂态稳定性的影响。

1）系统正常运行时。

由1.2 节可知，双馈风机在正常状态运行时等值为负电阻，通过分析风机等值电阻与风速的关系，进而分析系统在正常运行情况下风速对系统暂态稳定性影响。

风机机械功率PM的表达式[13-14]为

式中：CP为功率系数，表示流过风力机的空气动能中转换为机械能所占的比例，是桨距角和叶尖速比的函数，（R是叶片半径，ω是风力机转速）；A为叶片扫风面积；ρ为空气密度；v为风速。

风机在正常状态运行时，风电机组注入系统的有功功率Pe与风力机的机械功率PM相等。当风速一定时，Pe可通过式（12）求出。

双馈风机发出的有功功率主要与风速有关，不同风速下，风电机组与风速的关系及运行区域见图5。

图5 风机转速控制规律Fig.5 Control of DFIG revolution

第1 个运行区域是风力发电机的启动阶段，启动风速一般为6 m/s。第2 个运行区域是风机在并网发电运行的区域。该运行区域可分为两个阶段，分别为最大风能跟踪阶段和转速恒定阶段。最大风能跟踪阶段风速范围一般在6～11 m/s 之间，转速恒定阶段风速范围一般在11～12 m/s 之间。第3 个运行区域为功率恒定区，额定风速一般取12 m/s。为防止发电机和变换器达到功率极限出现损坏，通过风机桨距控制系统控制风机在额定风速下运行，通过限制风力机机械功率来维持发电机功率恒定。

由以上分析可知，系统在正常运行时，当风速低于额定风速在6～12 m/s 间波动时，当风速变大，风功率变大，风机注入系统的有功功率变大。根据式（1），当有功功率变大时，风机等值的电阻变小。由2.1 节中分析的在系统正常运行状态下风机等值电阻r与系统暂态稳定的关系可知，当风机等值电阻r变小时，风火打捆系统的暂态稳定性降低。由上述分析可得出结论：当系统正常运行时，风速的增大会削弱风火打捆系统的暂态稳定性。

2）系统发生短路故障时。

双馈风机在故障期间等值为负电阻和负电抗的并联，根据上文分析可知，风机的等值电阻与风机发出的有功功率Pe有关，当风速增大时，风功率变大，风机的等值电阻r变小。而风机等值电抗则与风机发出的无功功率Qe有关。无功功率由风电机组的无功控制方案决定，受到转子侧变流器最大电流和电机容量的限制。根据文献[14]可知：

式（13）为一空间曲面方程，其在Pe-Qe平面的投影就是变速恒频风电机组的无功功率限制范围。当风电机组的有功功率处于Pe在0-Prating之间，相应的无功功率可以由式（13）求得。

风电机组注入系统有功功率变化时，其无功功率变化曲线见图6。由上述分析可知，风机注入系统的有功功率随风速的增大而增大，无功功率随风速的增大而减少。

图6 双馈风机无功-有功关系图Fig.6 Reactive-active relation diagram of DFIG

当系统发生故障时，如果此时风速发生波动，由上文的分析可知，风电机组注入系统的有功功率随风速的增大而增大，无功功率随风速的增大而减少。由图6 有功-无功关系图可以看出，无功功率减少的幅度小于有功功率增加的幅度。由式（1）可得，随着风机注入系统的有功功率增加，无功功率减少，此时风电场等值的电阻r减小，等值的电抗x增大，等值电抗x增加的幅度小于电阻r减小的幅度。由2.1 节分析的在系统故障运行状态下风机等值参数r和x与系统暂态稳定的关系可知，r减小会提高系统暂态稳定，x增大会降低系统的暂态稳定，但由于等值电抗x增加的幅度小于电阻r减小的幅度，所以在整体上，风速的增大会提高系统的暂态稳定性。

3）系统故障切除后。

系统在切除故障后的分析原理和结论与系统在正常运行状态时一致[15-24]。所以当风火打捆系统故障切除后，风速的增大会削弱风火打捆系统的暂态稳定性。

通过以上分析可以看出，在系统正常运行阶段、系统发生故障阶段和系统切除故障后，风速的增大都会降低风火打捆系统的功率极限，削弱风火打捆系统的暂态稳定性。

3 限流式SSSC的控制策略

通过双馈风机的等值参数r、x结合系统具体的网络结构参数计算出限流式SSSC 在正常运行状态和故障切除后的SSSC 最佳补偿容抗Xs以及发生故障时限流电阻RF的值。Xs与RF为线路电抗XL和风机等值参数r、x的函数。通过限流式SSSC 的控制策略减小加速面积，增加减速面积，达到改善系统功角稳定性的目的。

3.1 正常运行情况下的控制分析

计算式（15）中限流式SSSC 的最佳补偿容抗时，根据不同风功率所对应的等值电阻r的值取值来计算XS，此时SSSC 的控制框图见图7。当风功率变化时，XS进行补偿，当超出SSSC 的最大补偿容量时，用SSSC 最大容量补偿即可，使风火打捆的暂态稳定性达到最优。

图7 SSSC双闭环控制系统框图Fig.7 Block diagram of SSSC double closed loop control system

图中,Uc为直流侧电压；Udcref为直流侧电压的参考值，其值由阻抗控制器给出；Xsssc为SSSC 的输出电压；M为调制比；θ为线路电流相位；α为控制角；Xref为线路阻抗的参考值；X为线路有效阻抗。采用PID 控制器来补偿X 的任何偏差，控制方程为

式中，Kp、Ki、Kd为PID 控制器的参数。

3.2 短路故障下的控制分析

在系统发生短路故障时，限流式SSSC 中的SSSC 模块已被切除，主要由限流电阻RF工作。由式（10）可以看出，|是关于限流电阻RF的函数，对RF进行求导公式为

系统发生短路故障时，由于故障时间很短，故可忽略在故障期间风速波动带来的影响，利用限流式SSSC 来改善由于短路前风速为达到额定风速和短路带来的系统暂态稳定性问题即可。限流式SSSC 中限流电阻为可调电阻，当系统发生短路故障时，通过调节RF的值使同步机组互阻抗的模值达到最小，提高风火打捆系统的功率传输极限，提高系统的暂态稳定性。

3.3 故障切除后的控制分析

故障切除后，SSSC 模块再次投入工作，此时送端同步机组互阻抗的模值|Z12|如式（11）所示，对Xs进行求导可得

故障切除后，系统的运行方式同系统正常运行时一致，用限流式SSSC 中的SSSC 模块来改善系统的暂态稳定性，所以控制框图同系统正常运行时一致，见图7。此时由于系统切除了一条线路，所以线路阻抗值发生变化，限流式SSSC 的最佳补偿容抗Xs可以通过式（20）计算得出。通过调制比M来进行调节，得到理想的线路阻抗值，提高风火打捆系统的暂态稳定性。

通过以上分析，设计系统中限流式SSSC 的控制策略如下：

1）正常运行时，令限流式SSSC 中SSSC 呈容性，根据2.2 中所述的不同风速，计算不同风速下所对应的SSSC 补偿度k，补偿度k的公式为

式中：Xc为SSSC 补偿等效容抗；XL为未补偿前线路电抗。

由文献[15]可知SSSC 的补偿度k的范围为0.2～0.75，由3.1 中风机不同工作风速区域可知，风机启动工作风速为6 m/s，通过计算可知当风速小于6.25 m/s 时补偿度大于0.75，所以当风速为6～6.25 m/s时，k取0.75。当风速超过12 m/s 时，由双馈风机的桨距控制系统限制风力机机械功率的输出维持发电机功率恒定。其他不同风速下SSSC 的补偿度见表1。

表1 SSSC的补偿度kTable 1 Compensation degree k of SSSC

在各风速区间利用牛顿插值法计算不同风速下对应的补偿度k，SSSC 的补偿度k的计算公式见表2。

表2 SSSC的补偿度k计算式Table 2 Calculation formula of compensation degree k of SSSC

2）故障运行时，通过系统参数计算出RF对线路进行补偿。

3）故障切除后，由于切除了一条线路，线路阻抗变大，通过计算可知此时的补偿度k都大于0.75，所以当故障切除后补偿度k取0.75。

4 仿真验证

为了验证上文分析的限流式SSSC 的控制策略提高风火打捆系统暂态稳定的作用，利用Matlab 仿真软件对图8 风火打捆仿真系统图中的风火打捆单端送电系统进行仿真验证[16]。

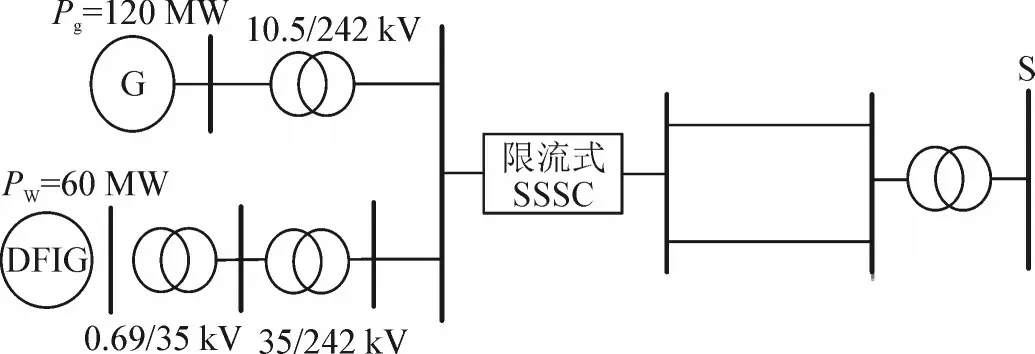
图8 风火打捆仿真系统图Fig.8 Diagram of wind-thermal binding power simulation system

风电机组和火电机组分别经图中所示的变压器变换电压后并联将电能经串联限流式SSSC 的双回线送入系统。风火比例设定为1:2，同步机组容量为120 MW。风电场包含40 台额定容量为1.5 MW的双馈风机，额定运行下风电场的有功出力为60 MW。分别设定风火系统在7 m/s、9 m/s 和11 m/s 的风速下运行，设定系统总运行时间10 s，在4 s 时在线路始端发生三相短路故障，故障持续时间为0.2 s，在4.2 s 后切除故障。正常运行时，根据表1 与表2 中SSSC 的补偿度，Xs与RF的取值分别见图9-10，当风速为7 m/s 时，Xs=-20.17 Ω ；风速为9 m/s 时，Xs=-22.73 Ω；风速为11 m/s 时，Xs=-23.11 Ω。故障期间根据式（18），RF的取值见图10 所示，故障发生时风速为7 m/s 时，RF=15.46 Ω ；风速为9 m/s时，RF=7.68 Ω；风速为11 m/s 时，RF=5.16 Ω。仿真结果见图11-13。

图9 Xs 取值图Fig.9 Xs value graph

图10 RF 取值图Fig.10 RF value graph

图11 故障时风速恢复为7 m/s仿真图Fig.11 Simulation diagram of recovery wind velocity of 7 m/s in the fault

图12 故障时风速恢复为9 m/s仿真图Fig.12 Simulation diagram of recovery wind wind velocity of 9 m/s in the fault

图13 故障时风速恢复为11 m/s仿真图Fig.13 Simulation diagram at recovery wind velocity of 11 m/s in the fault

由仿真可看出，风火打捆系统未加入限流式SSSC 运行在正常状态下，风速分别为7 m/s、9 m/s和11 m/s 时，初始功角分别为49.66°、52.62°、58.52°，初始有功功率分别为55、52、49 MW，初始转速分别为1.205、1.201、1.198 p.u.。可见随着风速的增大，系统功角增大，有功功率和转速下降，系统的暂态稳定性下降。在加入限流式SSSC 后初始功角分别下降为47.32°、50.73°、56.69°，再加入控制策略后初始功角分别再次下降为45.36°、47.78°、53.83°。由此可知，在加入限流式SSSC 控制策略后，系统采取限流式SSSC 控制策略后削弱了风速对系统暂态稳定性带来的不利影响，提高了系统在正常运行时的暂态稳定性[17-18]。

风火打捆系统发生故障和故障切除后的仿真结果见表3-5。

表3 故障时风速恢复为7 m/s仿真结果Table 3 Simulation result at recovery wind velocity of 7 m/s in the fault

表4 故障时风速恢复为9 m/s仿真结果Table 4 Simulation result at recovery wind velocity of 9 m/s in the fault

表5 故障时风速恢复为11 m/s仿真结果Table 5 Simulation result at recovery wind velocity of 11m/s in the fault

由表3-5 的仿真结果可知，在系统发生短路故障时，随风速的增大，系统未加入限流式SSSC 的功角峰值降低，转速峰值增大，有功功率的跌落值增大。即风速增大，系统的暂态稳定性提高；反之风速减小，系统暂态稳定性降低。系统在风速为7 m/s发生短路故障时，在采取限流式SSSC 控制策略时系统的功角峰值比未加入限流式SSSC 和加入限流式SSSC 但未加控制策略的功角峰值分别降低了24.6°和13.88°；转速峰值分别降低了0.016 p.u.和0.008 p.u.；有功功率的跌落值分别提高了13 MW 和8 MW。当系统在风速为9 m/s 发生短路故障时，在采取限流式SSSC 控制策略时系统的功角峰值比未加入限流式SSSC 和加入限流式SSSC 但未加控制策略的功角峰值分别降低了26.15°和16.67°；转速峰值分别降低了0.016 p.u.和0.005 p.u.；有功功率的跌落值分别提高了11 MW 和7 MW。当系统在风速为11 m/s 发生短路故障时，在采取限流式SSSC 控制策略时系统的功角峰值比未加入限流式SSSC 和加入限流式SSSC 但未加控制策略的功角峰值分别降低了24.57°和12.88°；转速峰值分别降低了0.039 p.u.和0.009 p.u.；有功功率的跌落值分别提高了16 MW 和10 MW。由以上分析可知，当发生故障风速在不同值时，通过限流式SSSC 的控制策略，在不同风速下控制RF的阻值，使其消耗有功功率，继而提高系统功率输送能力，削弱由于风速变化带来的系统暂态不稳定问题。

系统在切除故障后，风火打捆系统未加入限流式SSSC 时，系统功角的振荡曲线中心线值在风速为7 m/s 最低，在风速为11 m/s 最高；有功功率、转速的振荡曲线中心线值在风速为7 m/s 最高，在风速为11 m/s 最低。由此可见，在系统切除故障后，风速越大系统的暂态稳定性越差。在系统加入限流式SSSC 后，系统的功角、有功功率、转速的振动曲线小幅缓慢震荡。在采取限流式SSSC 的控制策略后，系统的功角、有功功率、转速的振动曲线在经过短暂的小幅震荡后逐渐平稳[19-20]。由上述分析可知，系统在故障切除后加入限流式SSSC 控制策略后，削弱了风速对风火打捆系统暂态稳定性带来的不利影响，提高了风火打捆系统功率传输极限，改善了风火打捆系统的暂态稳定性。上述仿真结果表明了利用限流式SSSC 控制策略可以削弱系统不同运行阶段风速对系统暂态稳定性的影响，提高了系统的暂态稳定性。

5 结语

本文通过借助双馈风电机组等值外特性参数构造含SSSC 的风火打捆系统暂态稳定数学模型，分析风速对风火打捆系统暂态稳定性的影响，并根据不同影响采取相应的控制策略提高风火打捆系统暂态稳定性。

通过建立含限流式SSSC 风火打捆系统的功率方程分析风机等值参数对系统暂态稳定的影响，进而基于风机等值参数来分析风速对系统暂态稳定性的影响并进行仿真验证，说明系统在正常运行和切除故障后，随着风速的增大风机等值电阻变小，降低了系统功率传输能力，继而削弱风火打捆系统的暂态稳定性；系统在发生故障时，随着风速的减小系统的功率传输极限降低，降低了系统的暂态稳定性。

根据系统不同运行状态下风速对系统暂态稳定性影响的不同提出相应的限流式SSSC 控制策略。正常运行和故障切除后，控制SSSC 等值电抗为容抗，等值容抗随风速的增大而增大，减小了线路等值电阻，提高系统功率传输能力，削弱了风速对系统暂态稳定性的不利影响；短路故障发生时控制限流式SSSC 为电阻，使限流电阻随风速的增大而减小，电阻消耗一定的有功功率，提高系统的功率传输极限，提高了风火打捆系统的暂态稳定性。