基于最优K 均值聚类算法的负荷大数据任务均衡调度研究
白雨佳,李靖,高升
(1.国网内蒙古东部电力有限公司信息通信分公司,呼和浩特 010020;2.中国科学院沈阳计算技术研究所有限公司,沈阳 110000)
0 引言
由于因特网技术的飞速发展,网络中共享的资源越来越多,资源的种类越来越多,各种资源被广泛引用,如何有效地传输多源数据成为相关学者亟待解决的重要问题,传统的多源大数据在进行预取时,往往会出现多个节点输出相同结果的情况,从而导致资源竞争现象的发生[1]。为避免出现上述问题,迫切需要研究多源大数据均衡调度的新方法。跨源资源调度方法是一种有效的调度方法[2-3]得到了人们的广泛关注。
为此,王慧等人[4]提出了基于小波分析的大数据调度方法,该方法通过小波分析对电力大数据去噪后,以去噪数据完成优先级列表控制模型构建,并完成负载均衡传输信道模型的建立,通过自适应加权控制方法和时隙分配获取最佳目标函数,完成数据调度,但是该方法的时间开销较大;周生奇等人[5]研究了基于灰色模糊预测的大数据调度方法。该方法采用灰色模糊预测方法完成多服务器中的流动数据的调度,但是该方法在调度过程中,负荷大数据的均衡度不够理想。
为确保电力负荷大数据的准确调用,需进一步明确数据的类别和数据信息,因此需划分电力负荷数据。K 均值聚类算法为迭代求解聚类分析算法的一种,并且是应用广泛的划分聚类算法,其应用过程简洁且效率较高。因此本文选择K 均值聚类算法对电力负荷大数据实行分类。基于此,本文研究基于最优K 均值聚类的电力负荷大数据跨源调度方法,以期实现较小开销下的电力负荷大数据调度。
1 电力负荷大数据跨源调度
1.1 基于最优K均值聚类的电力负荷大数据分类
1.1.1 K 均值聚类算法
K 均值聚类算法的核心为:设数据对象数量为n,对其实行划分处理,共分为k个类,使全部数据对象距离该类的聚类中心点平方和为最小。
设算法的输入数据集为F={x1,x2,...,xn},算法的输出为k个类,即{F1,F2,...,Fk},且保证最小平方误差准则。算法步骤如下所述:
1)设数据样本为X,初始聚类中心cj为随机选取的数据对象,其中j=1,2,...,k。
2)为获取X中的各个对象xi至k个聚类中心cj的距离,计算欧式距离公式为
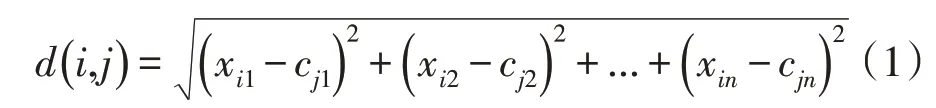
3)获取cj(n+1)的值,并将其作为新聚类中心点[6]:计算公式为

式中,Nj为第j个类中心数据对象的数量。
4)判断准则是否满足,若满足,则转至步骤2),反之转至步骤5)。根据判断准则可知,两次迭代获取的聚类中心点相同,且聚类离散度不会再发生变化。由此可建立聚类离散度函数为
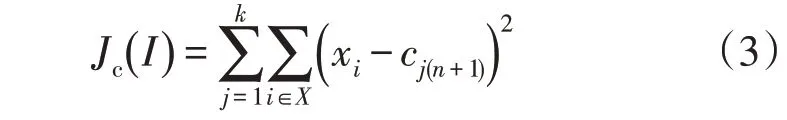
5)输出聚类结果。
1.1.2 聚类中心优化
上节中的K 均值聚类算法虽然可快速完成聚类,但是其聚类不是最优结果。由于其初始聚类中心点是通过随机选取K 个数据对象完成,通过迭代计算寻优,直至符合收敛条件[7]。因此,初始中心点的差别会导致聚类结果出现差异性,导致聚类效果不稳定、结果不是全局最优解,甚至还会降低算法的效率。
基于上述分析,K 均值聚类算法初始中心点的优化尤为重要,实现依据聚类对象自动完成k值估计。K 均值聚类算法利用优化后的最优聚类中心完成电力负荷的分类[8],获取合理、准确的分类结果。本文采用密度法优化K 均值聚类算法初始中心点,其将初始聚类中心用k个位于高密度区域且相互距离最远的点表示。优化的算法可有效抑制噪声点对聚类算法的影响。
该算法在优化过程中,需计算每一个数据对象的密度参数,并以其为标准,将选取k个值较高的对象作为初始聚类中心[9-11]。优化后算法的计算步骤如下:
1)待处理样本数据集合为F={x1,x2,...,xn},k个初始聚类中心点为z1,z2,...,zk。
2)通式(1)对任意对象xi到聚类中心之间的欧式距离求解。
求解计算对象之间的平均距离,其计算公式为

式中,n和分别为数据对象的数量和任意两个对象组合的总数量。
MeanDist 作为计算对象密度参数的一个关键量,以式(4)为依据,则任意两个数据对象之间距离的平均值通常作为其值的选取,但在特殊条件下,可在一定范围内对其进行调整[12-13]。
3)为获取各个对象的密度参数density(p,)MeanDist 采用式(5)完成。
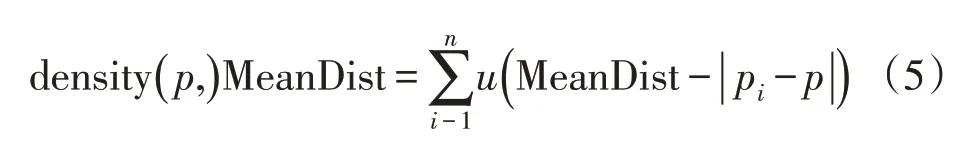
4)寻找密度参数最大值所对应的数据对象,将其作为第1 个初始聚类中心,同时将该聚类中心之间距离小于MeanDist 的数据对象的密度参数从D中删除[15]。
5)重复步骤3)和步骤4),停止条件为获取到密度参数较大的k个数据对象为止,并将该对象作为初始聚类中心点[16-17]。基于密度方法优化初始中心点的计算流程图见图1。
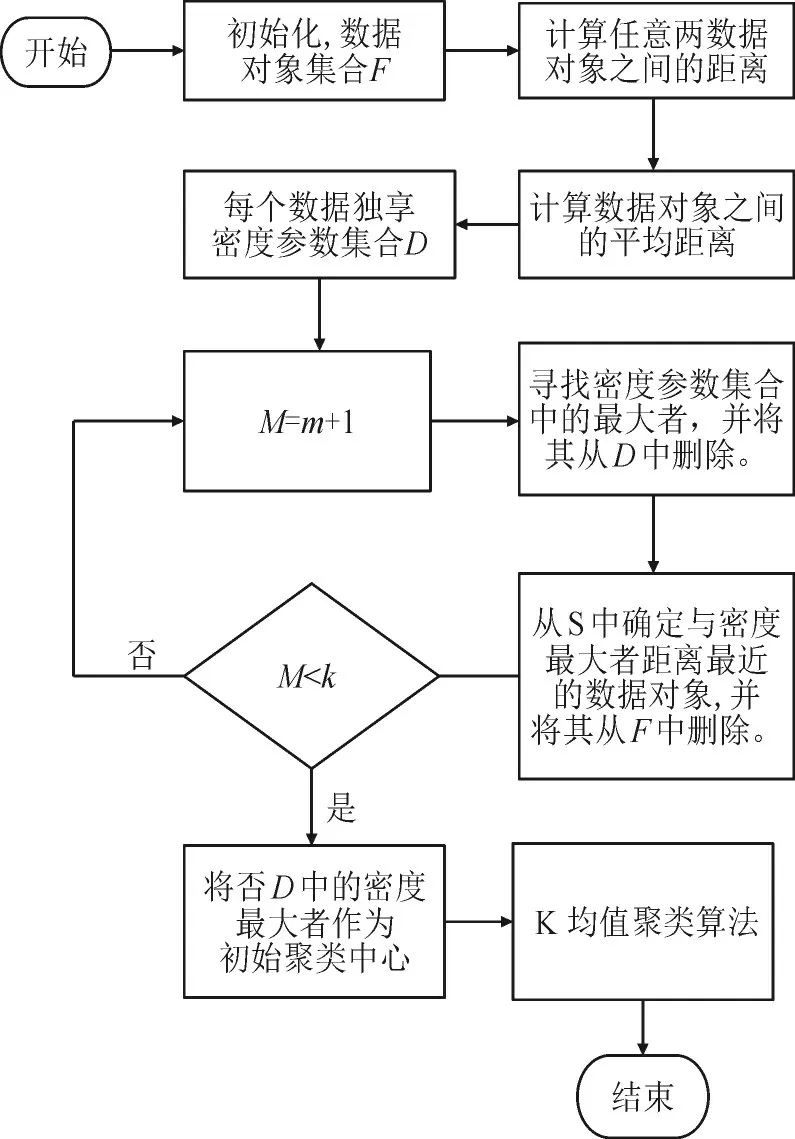
图1 优化聚类初始中心点流程Fig.1 Initial center point flow process of optimization clustering
1.2 电力负荷大数据跨源调度
1.2.1 关联特征提取
基于电力负荷大数据聚类结果,结合基于权重的跨源调度方法,对聚类后的电力负荷大数据实行跨源调度[18],获取电力大数据跨域调度的输出特征量为
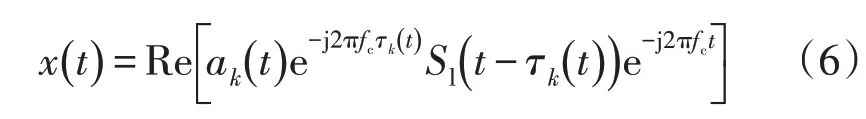
资源调度负载均衡特征向量在支持向量机学习模式下可表示为
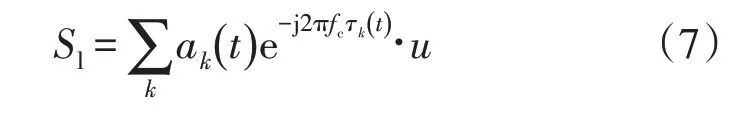
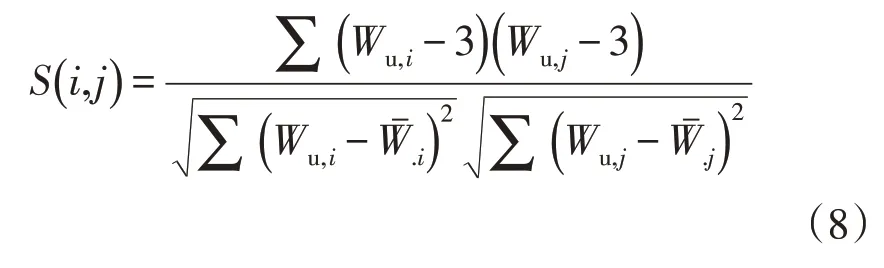
式中,Wu,i和Wu,j分别为分类得到的数据输入集和数据聚类中心的电力负荷大数据评价矩阵[21],则电力负荷大数据分布集的优化关联特征为
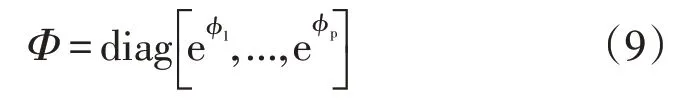
1.2.2 大数据跨源调度输出
在支持向量机学习模式下,利用自适应权重学习方法完成电力负荷大数据跨源调度的寻优控制[22-23]。电力负荷大数据跨源调度的主特征决策树用四元组(Ei,Ej,q,t)表示,其中,电力负荷大数据在有向图中的分岔节点分别为Ei和Ej,获取电力负荷大数据的差异化融合特征量,其公式为
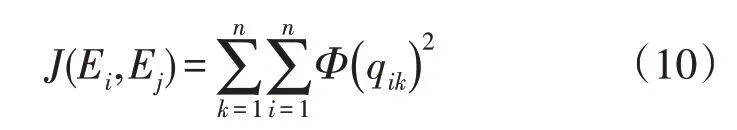
式中:m为电力负荷大数据分布的有限数据集;(qik)为相似度分布映射[24]。电力负荷大数据的相似度分布映射计算公式为
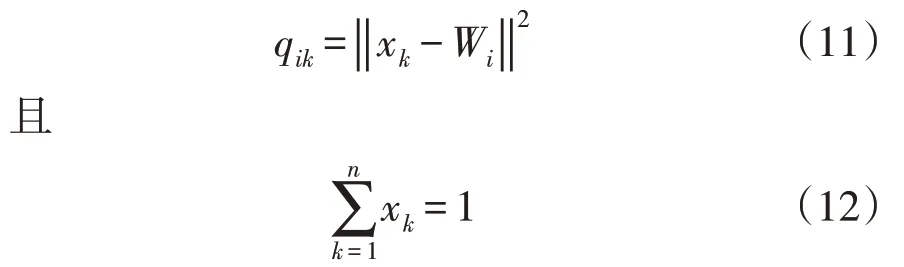
对电力负荷大数据实行优化调度和挖掘处理[25-32],则获取电力负荷大数据调度均衡的输出模型,其公式为

根据上述步骤,完成电力负荷大数据的跨源调度处理模型构建。
2 实例分析
为测试本文方法的应用性能,选取某电网企业中1 000 个不同用户,将这些用户按照每天每时的用电负荷按照由低到高排列,具体数据见表1,数据单位为kW·h。
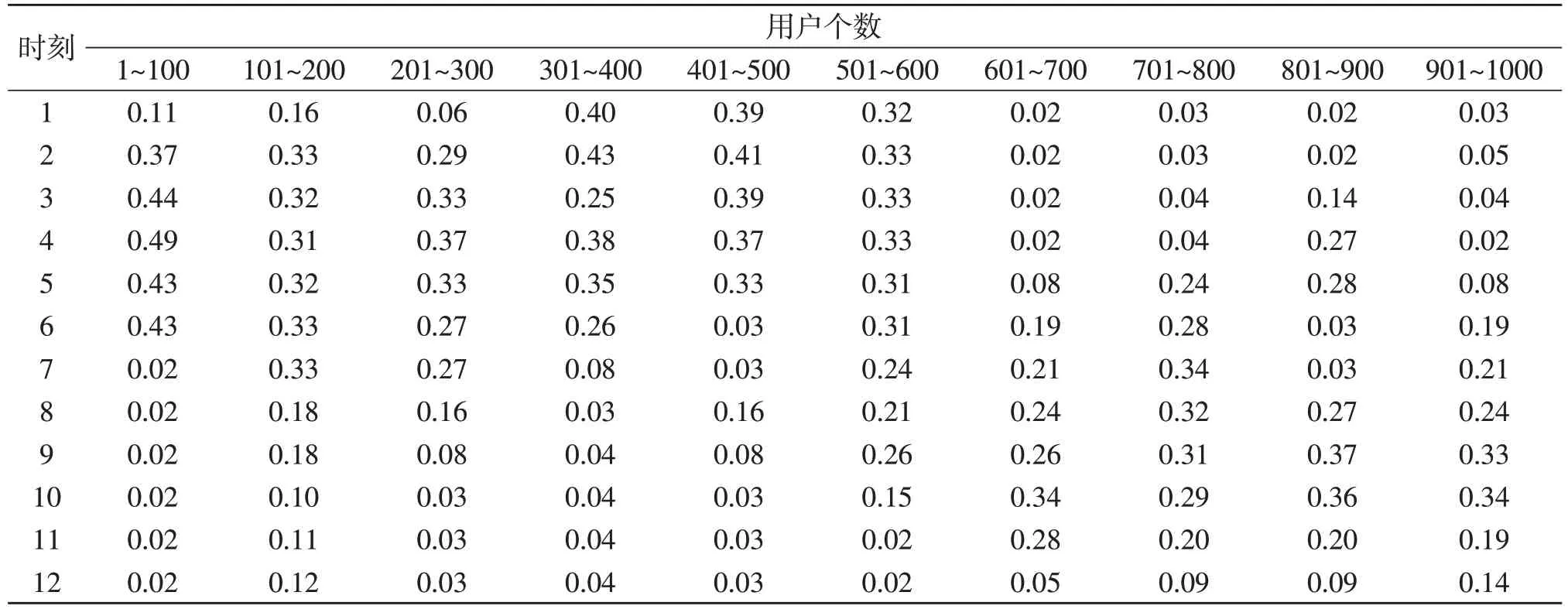
表1 用户用电日负荷数据Table 1 Daily load data of power consumption of user kW·h
聚类的类别数k的取值对于负荷大数据分类的结果存在较大影响,因此需确定最佳k值,测试不同k值时,聚类结果见图2。
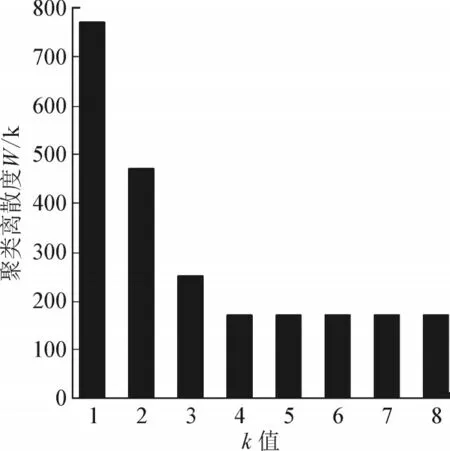
图2 测试结果Fig.2 Test result
根据图2 的测试结果可知:当k值达到4 以后,聚类离散度平稳不再发生变化,因此,为保证电力负荷大数据分类结果准确,k值取值为4,下述实验中,该值均为4。
采用本文方法对表1 数据进行分类,分析本文方法的分类结果,见表2。
根据表2 的测试结果可知:第1 类用户和第2 类用户负荷波动均较小,波动范围分别在0.14~0.25/kW·h和0.03~0.12/kW·h,其中负载较高的时间范围在9~12 时和1~3 时;第3 类用户负荷波动较大,波动范围在1~10 时,说明该用户夜间用电较多;第4 类用户负荷波动也较小,并且相对平稳。根据该结果可说明:本文方法可根据不同的电力负荷大数据特点,有效完成用户电力负荷大数据分类,具备较好的分类效果。
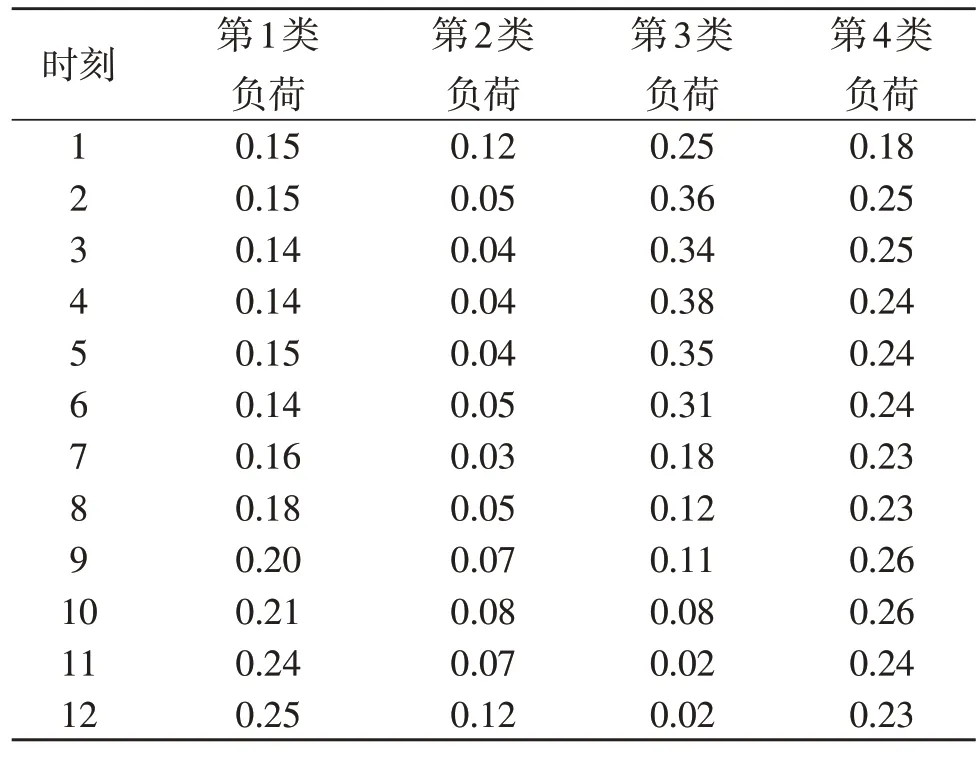
表2 电力大数据分类结果Table 2 Classification result of power big data kW·h
将文献[4]和文献[5]的基于小波分析的大数据自适应延迟调度方法和基于灰色模糊预测的大数据调度方法作为本文方法的对比方法,统计3 种方法调度的负载均衡度,结果见图3。
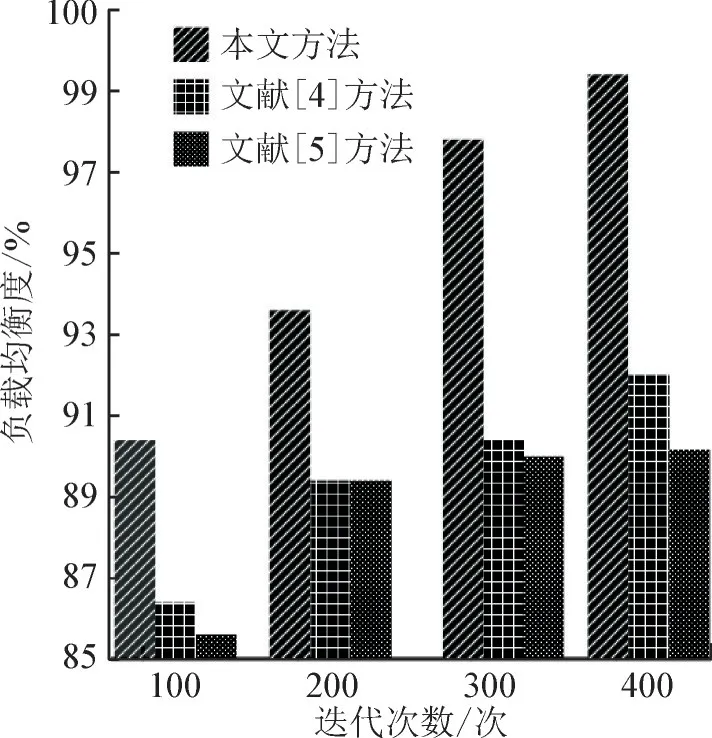
图3 3种方法调度的负载均衡度对比结果Fig.3 Comparison of load balancing degree of three methods
根据图3 测试结果可知:在相同迭代次数条件下,本文方法调度的负载均衡度优于两种对比方法;随着迭代次数的增加,3 种方法调度的负载均衡度均呈现上升趋势,但是,本文方法的调度后的负载均衡度结果依旧优于两种对比方法。说明本文方法调度后的负载均衡度较好,具备良好的大数据跨源调度均衡性。
采用均衡负载离差进一步衡量3 种方法的跨源调度性能,其计算公式为

式中:LBj和分别为处理器调度前负载和调度后负载;m为数据量。
利用式(15)获取3 种方法在不同调度任务量条件下的负载均衡离差结果,见图4。
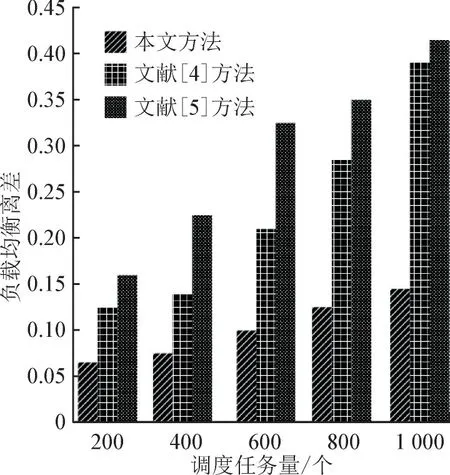
图4 3种方法的对比结果Fig.4 Comparison result of three methods
根据图4 测试结果可知:在调度任务量相同的情况下,本文方法的电力负荷大数据跨源调度负载均衡离差均低于两种对比方法;随着调度任务量的增加,3 种方法的负载均衡离差均呈现上升趋势,但是本文方法的上升趋势相对平缓,并且依旧低于两种对比方法,当调度任务量达到1 000 个时,负载均衡离差也低于0.15,说明本文方法的跨源调度负载均衡较好,调度性能较好。
调度开销是衡量调度性能的主要指标,统计3种方法在不同大小数据调度情况下所需的调度时间开销,结果见图5。
根据图5 的测试结果可知:3 种方法在调度数据量相同时,调度开销结果中,本文方法的开销最低,均低于0.95 s;随着调度数据量的增加,两种对比方法的调度开销呈现明显上升趋势,本文方法则相对平稳,调度开销没有明显增加。说明本文方法可有效降低调度延迟和时间开销,适用性较高。
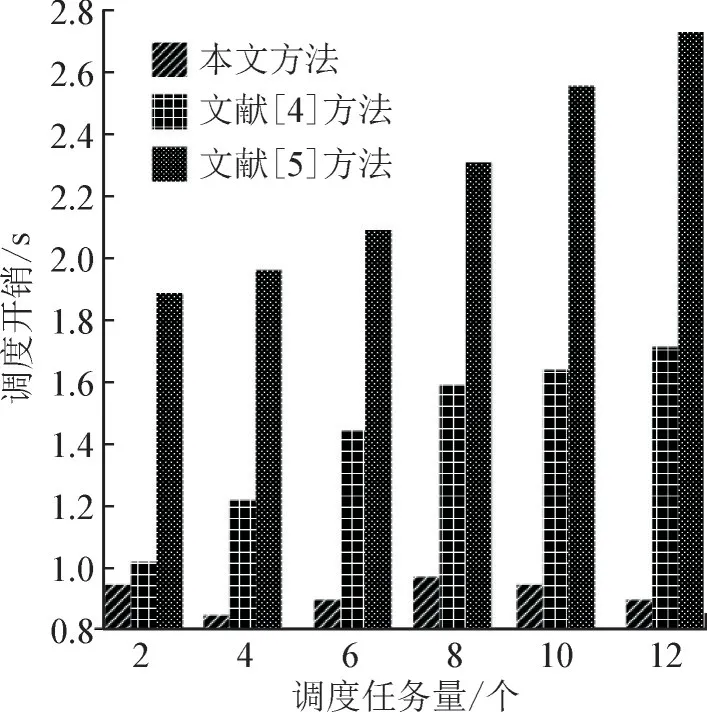
图5 3种方法的调度开销对比结果Fig.5 Comparison result of scheduling cost of three methods
3 结语
随着电力系统的发展,负荷数据日益复杂,且用户类型多样化,使得当前电力用户的负荷调度成为一大难题。本文研究基于最优K 均值聚类的电力负荷大数据跨源调度方法,满足电力企业用电需求的同时保障电力负荷均衡度。经实验测试表明:本文方法在k值为4 时,可获取最佳电力负荷大数据分类结果,并且调度均衡度较好,调度时的开销较低,可有效完成电力负荷大数据的均衡调度。

