基于滞环电压模型的锂离子电池SOC 估计
周文钊,夏向阳,陈彦余,张嘉诚
(1.长沙理工大学电气与信息工程学院,长沙 410114;2.规模化电池储能应用技术湖南省工程研究中心,长沙 410009)
0 引言
近年来,随着新能源发电技术的迅速发展,越来越多新能源接入电网,使电力系统稳定性面临着巨大的挑战[1]。为了满足电网稳定性的需求,电力储能技术应运而生。现有电力储能技术通常可以分为3 类:机械储能,电气类储能,电化学储能[2]。机械储能包括压缩空气储能、飞轮储能、抽水蓄能等;电气储能包括超级电容储能、超导储能等;电化学储能主要包括了各种电池储能,如铅酸电池、锂离子电池、钠硫电池、液流电池等等。在上述3 种电力储能方式中,电化学储能因其建设成本较低,技术相对成熟等优势广泛应用于电力系统中。而在电化学储能中,锂离子电池因其高能率密度,长循环寿命,低成本的优点成为当下电池储能材料本体的首要选择[3-4]。但是由于电池的荷电状态参数无法精确测量,因此需要电池管理系统(bottery management system,BMS)对其进行实时的估计。BMS[5]的一个主要功能就是提供电池荷电状态(state of charge,SOC)、健康状态(state of health,SOH)、内部阻抗等参数的估计值,这些参数可为故障诊断和电池系统的预测能力提供可靠依据。目前电池在线SOC 的估计方法主要有两类[6]:直接测量方法(即非基于模型方法)和基于模型的方法。直接的测量方法包括开路电压法和安时积分法[7-8],两类方法均简单易实现,但都有局限性。例如前者要求电池长时间静止并切断电源从外部电路测量开路电压(open circuit voltage,OCV),后者累积误差较大,随着时间推移估计结果不准确。若不考虑成本问题,基于模型的估计方法的准确度要大大优于直接测量法。而基于模型的估计方法又可以分为纯数据驱动的辨识模型和等效电路模型。其中,纯数据驱动的方法[9-11]能够较好的模拟储能电池的非线性,但是却需要大量的历史充放电数据来支撑模型的建立与优化,而估计的精度又非常依赖模型结构和优化方法,因此运算量极其庞大。等效电路模型结构简单,能直观反映电气特性,运算量相对小得多,因此在实际运用中,等效电路模型应用广泛。一般说来,电池模型越复杂,所用的辨识算法和估计算法运算量就会越大,同样估计精度也会越高[12]。目前大部分锂离子电池所采用的模型为一阶、二阶甚至三阶RC 等效电路模型,难以兼顾SOC 估计的精度和速度。一阶RC 模型又称为Thevenin 模型,采用一个RC 并联网络用以描述电池内部的极化反应。二阶RC 模型在一阶RC 模型的基础上又串联了一组RC 并联网络,用以区分电化学极化反应和浓差极化反应,但同时,模型变得更加复杂导致运算量大大增加[13-14]。考虑实际成本与估计方法的实用性,本文选取一阶RC 等效电路模型。文献[15-17]均采用了一阶RC电路模型,从实际仿真结果可以看出,文献[15]和文献[16]采用最优算法估计误差均能达到3%以内,但是接近真实值所需时间要数千秒,运算速度较慢。文献[17]达到真实值所用时间在1 500 s 左右,但是稳定性较差,后期估计值变化较大。因此,本文改良一阶RC 模型,采用带滞环单元的一阶RC 等效电路模型,应用快速UD 递推最小二乘法(FUDRLS)实时辨识模型参数。基于已识别的模型参数,采用迭代的平滑可变结构滤波算法(ISVSF)估计SOC。本方法可以精确估计锂离子电池SOC,其精度高、稳定性好、所需时间短,具有易实用性,可嵌入BMS 系统。
1 带滞环单元电池模型
本文改良一阶RC 模型,采用带滞环单元的一阶RC 等效电路模型,如下图1。
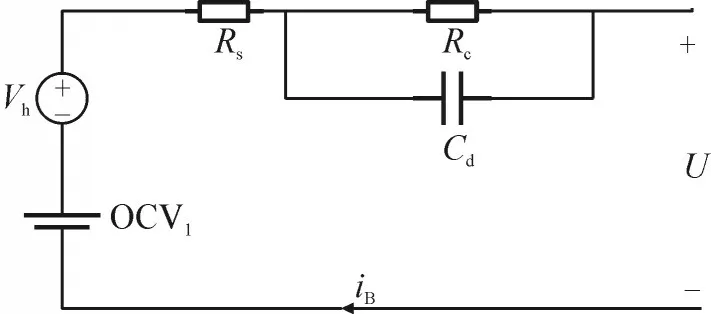
图1 滞环一阶RC等效电路Fig.1 First order RC equivalent circuit with hysteresis ring
在图1 中,电池开路电压OCV 包括两部分。第一部分,用OCV1表示,表示平衡OCV,为电池SOC外部开路电压。第二部分Vh为滞环电压,用于模拟OCV 的非线性。这个RC 电路模型能够比较准确描述电池I-V特性和瞬态响应。串联电阻Rs用于模拟电池充放电时能量电荷的转移损耗,扩散电阻Rc和扩散电容Cd用于模拟电池工作的短期扩散电压Vd[18],U表示电池的端电压。本文定义:

实时电池的离散状态空间方程为

式中:k表示某一时刻;x(k)为状态向量;y(k)是测量输出,为端电压;η为库仑效率(假设η=1);Ts为采样周期;iB(k)为k时刻充放电电流;Vhmax为最大滞后电压,也是SOC 的一个函数;ρ为系数,表示滞回电压变化速度;a0~a5为OCV 曲线的系数。
锂离子电池的SOC-OCV 拟合曲线见图2。
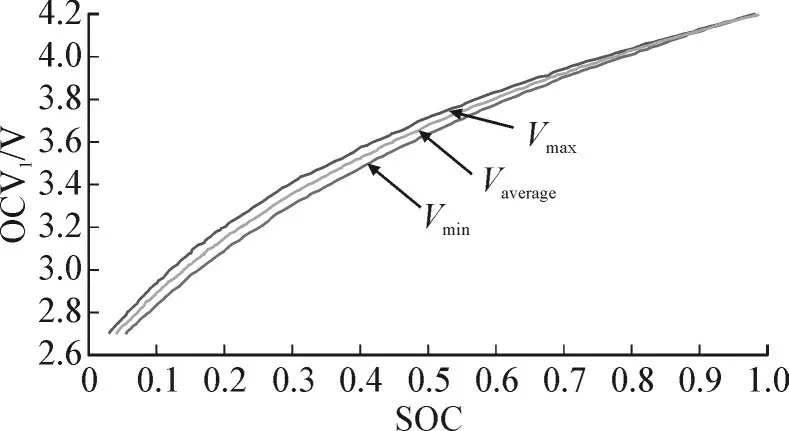
Fig.2 Fitting relationship betweenthebattery SOC and the external open circuit voltage OCV1图2电池SOC与外部开路电压OCV1拟合关系
图中,Vmax和Vmin分别表示电池在不同运行工况时候的开路电压上下限,造成同一SOC 对应外部开路电压(OCV1)的不同是由电池的迟滞现象造成的。取某时刻加上迟滞电压Vh作为电池开路电压,从而得到SOC-OCV 的最终拟合曲线。滞回电压Vh的一阶微分方程为
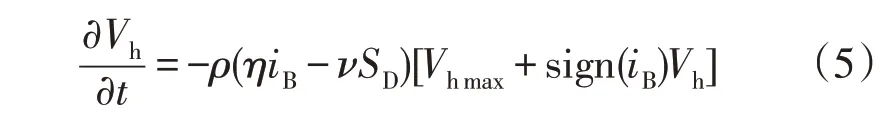
式中:ν为系数;SD为自放电率。
此滞后模型描述了滞后电压Vh与当下电流大小、方向、自放电倍率和滞后边界的关系。从表达式可看出,当电池运行在一个长期电流,或瞬时大电流的工况下,滞后电压将达到Vhmax[19]。从另外一个角度看,外部开路电压OCV1将慢慢达到Vmax;若电池工作在短时小电流,OCV1会慢慢降低到Vmin。加入参数ρ是为了尽量减小SOC-OCV 曲线的仿真与实际情况的误差。参数ρ和Vhmax的大小和电池SOC 以及温度有关[20]。在本文中测试电池时忽略了在环境温度下的温度相关性。
2 SOC估计算法
本文采用改进平滑变结构滤波算法(smooth variable structure filter,SVSF)的算法,应用一种迭代的迭代的平滑变结构滤波算法(iterative smooth variable structure filter,ISVSF)估计方法结合状态空间方程,通过反复迭代每个时刻的电池状态估计值,加快了算法的收敛的速度。这个状态空间模型的内部参数Rs、Rc和Cd由FUDRLS[21]在线参数更新识别算法得到,这会使得最终的SOC 估计值更加精确。SVSF[22-24]作为一种新的预测校正方法于2007年被提出,该方法基于变结构和滑膜理论,后被广泛应用于状态和参数的预测估计。该方法通过实现开关增益以保持估计的状态始终在有界域内,该有界域就是包含了电池真实状态不变量的集合。只要给出边界值,SVSF 就能够相对稳定准确模拟不确定性和误差。该算法估计的电池状态轨迹被强制朝向电池实际状态轨迹靠近,直到它到达实际状态轨道周围的子空间,即存在子空间[25]。而在此之前,SVSF 已应用于估计电池参数和SOC。本文在SVSF算法基础上,采用ISVSF 算法并结合式(1)、(2)状态空间方程,估计电池的荷电状态,公式为
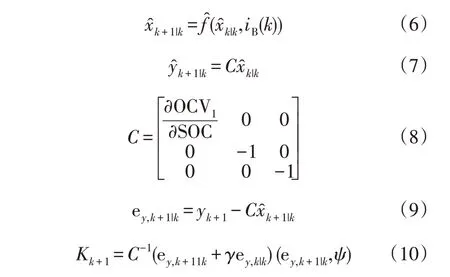
式中:+1|k为电池下一时刻状态估计的预测值;k|k为当前时刻的状态估计值;+1|k为k+1 时刻的测量参数;C为测量矩阵;ey,k+1|k为测量误差;Kk+1为k+1时刻结构增益;Ψ为平滑滤波边界层宽度;γ(0<γ<1)为算法收敛速度;°为舒尔乘积。该增益值应为正(即C>0),以确保数值稳定性。增益K用于修正状态估计值,则修正后的状态估计为:
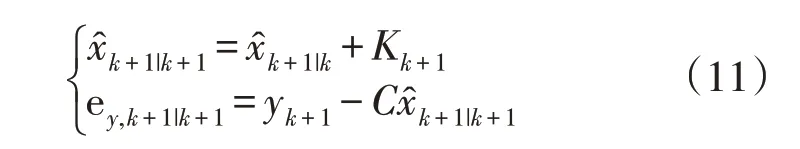
为了加快算法的收敛速度,应用迭代SVSF,他包括两个步骤:预测和更新。其中,预测步骤的公式同上述SVSF 的一致。若预测步骤误差ey,k+1|k+1高于原先设定的误差边界值,则进入更新迭代步骤,公式为
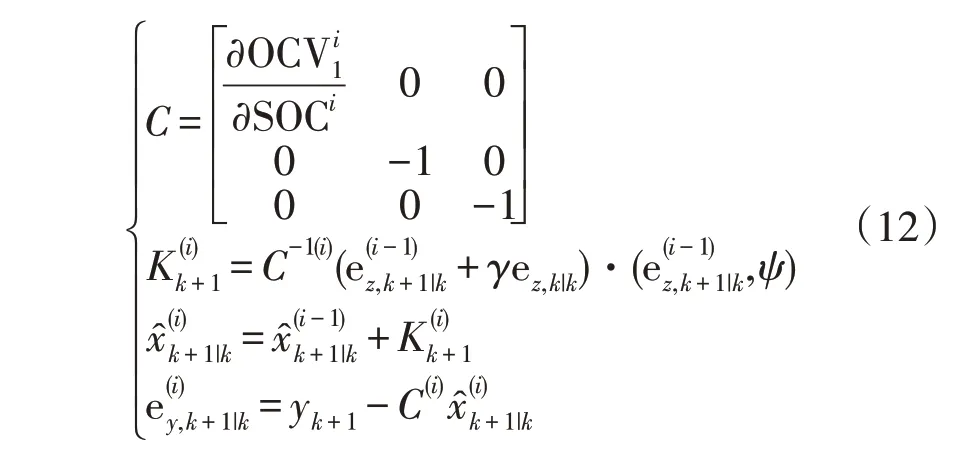
当得到的估计误差小于所设定的误差边界ζ 或者迭代次数i达到了最大设定值Nmax时,停止迭代。随着迭代步骤的进行,最终+1|k+1会收敛到某一个值。其中,误差边界值ζ和迭代次数Nmax的设定会直接影响ISVSF 的收敛速度。
3 实验验证
为了验证上述所提ISVSF 算法状态估计的效果,本文进行了不同脉冲电流作用的实验。实验所用电池为锂电池,其额定容量、标称电压和截止电压分别为5 AH、3.7 V 和2.5 V。在Matlab 中,电池电路模型参数设置见表1,电池的电压、电流等参数由电池测试仪收集得到,然后用上述提到的自适应平滑可变结构滤波进行电池状态估计。
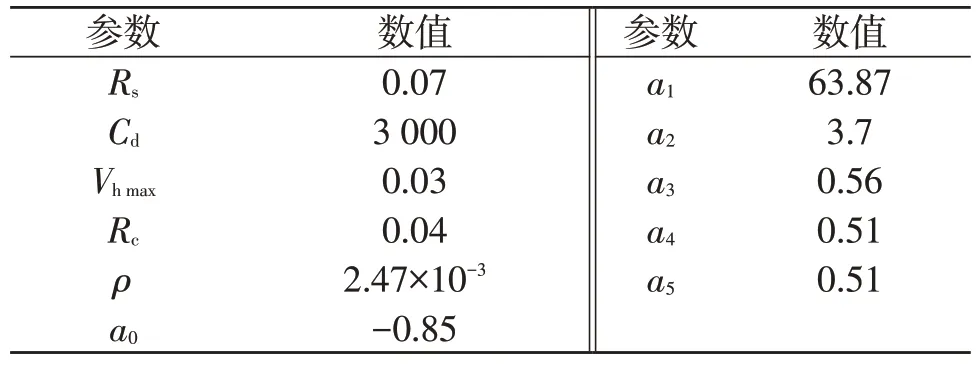
表1 模型参数Table 1 Model parameter
3.1 仿真分析
在Matlab 中,使用依据电池模型设定好的仿真数据并采用基于ISVSF 算法的SOC 估计方法进行仿真验证。后将仿真结果与基于传统扩展卡尔曼滤波算法(extended kalman filter,EKF)和SVSF 算法得到的SOC 进行对比[26-32],从而证明ISVSF 算法的优越性。为了验证各算法对SOC 估计初值的修正能力,最初将电池实际SOC 均设为0.5,而各算法的SOC 估计初值从0.6 开始。在EKF 中,系统噪声协方差和测量噪声协方差分别定义为0.016 和0.025。在SVSF中,γ和Ψ的值分别选为0.1 和1。对于ISVSF,γ和Ψ的值与SVSF 中的相同,而ζ 和Nmax分别设置为0.003 和10。电池充放电电流如图3 所示。图4~图6分别为用3 种算法估计得到的SOC、滞回电压Vh和扩散电压Vd同各真实值的比较图。根据图4-6,表2 对比了3 种算法的估计精度和运算速度,其中,估计精度由各算法所得参数与实际参数的均方根误差来表示,运算速度由各算法在统一配置计算机的所需仿真运算时间来描述。由表2 可证明,ISVSF具有最好的估计精度和较快的估计速度。
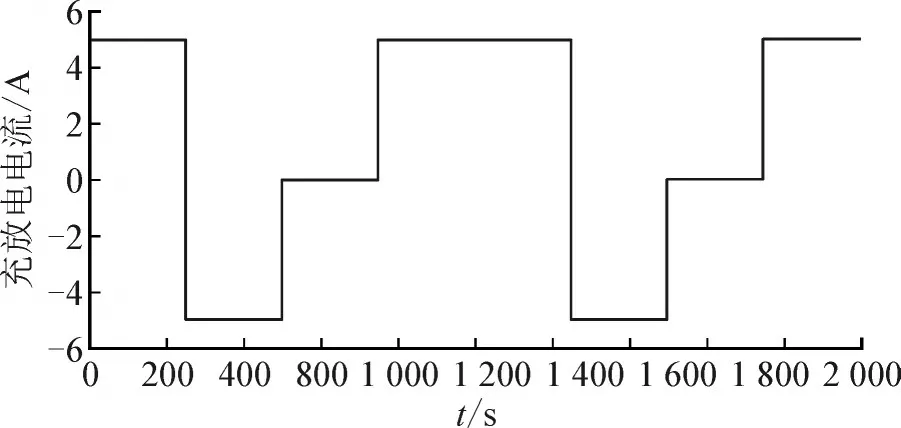
图3 仿真电池充放电电流Fig.3 Charging and discharging current simulation of battery
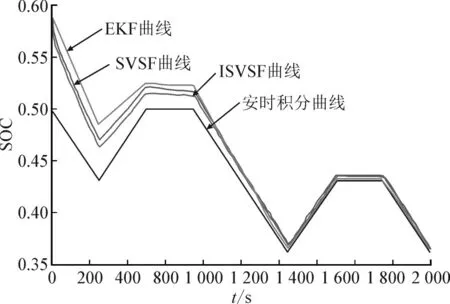
图4 各算法得到的电池SOC估计值Fig.4 Estimation value of battery SOC obtained by each algorithm

图5 各算法得到的滞回电压值Fig.5 Hysteresis voltage obtained by each algorithm
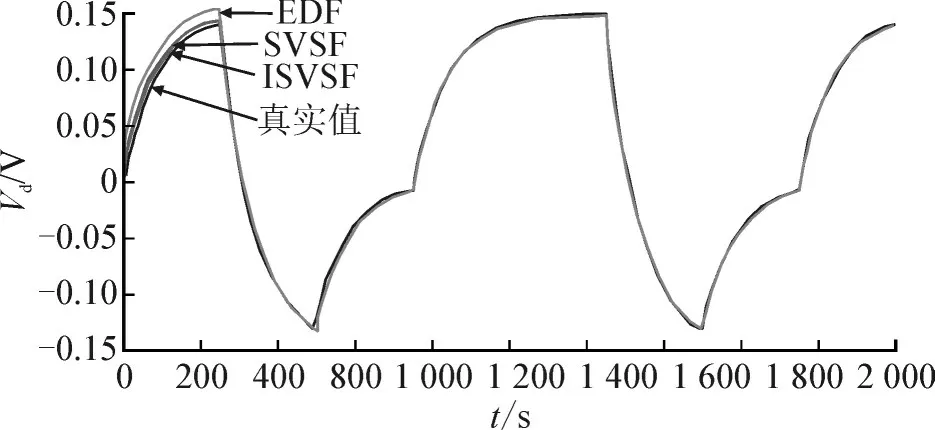
图6 各算法得到的扩散电压值Fig.6 Diffused voltage obtained by each algorithm

表2 各算法运算速度和运算误差Table 2 Operation speed and error of each algorithm
3.2 实验分析
本文方法应用于储能电站电池管理系统,可为电网削峰填谷的储能电池进行SOC 估计,因此不做复杂充放电实验,为了进一步证明所提ISVSF 在储能电站BMS 中的可行性,本文采用实验数据进行进一步分析。实验平台见图7,平台包括DIY 锂离子电池平衡充电器,带220 V 电源输入线,输出电压在2.70~4.85 V 可调,输出电流最大可调50 A,电池采用磷酸铁锂电池,充电截止电压3.5~3.8 V,理论容量为4.8 AH,出厂内阻为1 mΩ,另外包括一台上位机,直流电压电流表和导线若干。

图7 电池实验平台Fig.7 Experimental platform of battery
在本实验中,真实的SOC 值由起初已经设计的充放电电流通过安时积分法可以获得。在实验中,电池真实SOC 值是用安时积分法通过计算得来。在本实验中,γ和Ψ的值分别设为0.1 和1。此外,误差边界ζ 和迭代次数上限Nmax分别设置为0.01和10。电池初始SOC 值和最大容量在算法中不同于实际值分别设置为0.5 和5 Ah,而真实初始SOC和最大值采用安时积分法得到的值分别为0.3 和4.732 Ah。其中,为了获得真实的初始SOC,将电池首先充满电并静置一个小时,然后用小电流(0.2 A)放电至期望初始SOC 值0.5。实际使用的电池实际最大容量由充满电并静置过后的电池采用小电流0.2A 进行一个完整的放电实验获得。实验首先采用FUDRLS 辨识得到电路模型参数,再使用恒定采样周期一秒一次进行采样,用于电池的参数在线更新,以获得精准的参数用于ISVSF 算法。控制电池的充放电电流见图8。
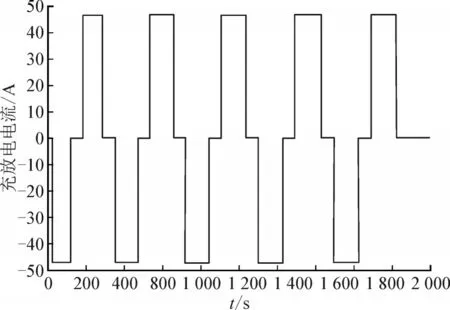
图8 实验电池充放电电流Fig.8 Charging and discharging current of experimental battery
图9 为应用ISVSF 算法且在初始值设定存在一定误差的情况下得到的SOC 估计值与实际根据电池充放电电流应用安时积分法得到的真实SOC 值的对比图。如图所示,在初始误差特别大的情况下,经过数十秒后能够将误差控制在5% 以内,1 000 s 后误差可控制在2%以内。实验结果表明该算法结合上述所提的带滞回电压的电池模型在SOC 估计中有较强的误差修正能力和较高的估计精度。
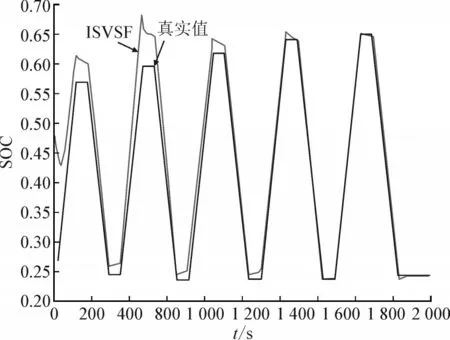
图9 实验SOC估计值与实际值Fig.9 Estimated and actual value of experimental SOC
4 结语
1)改进一阶RC 电路模型,将电池滞回电压作为一个参数辨识量单独提出后可以将SOC 估计误差控制在2%以内,且并没有大量增加算法的复杂度。
2)采用滞环单元电路模型估计电池SOC 时,ISVSF 算法相比较于SVSF 和EKF 在算法复杂度、运算速度和估计精度上有更好的综合能力,更适用于储能电池的SOC 估计。
3)本文所采用方法模型相较其他一阶RC 模型初始误差修正能力强,运算时间短,稳定性好,且算法不复杂,具有实用性,可嵌入各种电池储能场景中的电池管理系统。

