函数与规律探索相撞出思维火花
⦿浙江省杭州市萧山区高桥初级中学 施燕芬
1 问题提出
在平时的学习中,常常会碰到规律探索问题,这类问题一般给出一列数、一列式子或一列图形等形式,通过观察、比较、归纳、猜想的过程,寻求内在规律,然后依据规律加以运用.此类问题有效地考查了学生的逻辑推理、归纳猜想、发现探索,以及运用所学知识和方法分析、解决数学问题的能力,考查的数学思想有:特殊与一般、类比、数形结合、转化与化归.
一般规律题的解答是先找出相邻两项间的联系及各项中的数字与序号之间的关系,再从特殊到一般进行观察与猜想,得到一般规律.但是随着课改的不断深入,规律探索问题也有了新变化,面对新问题,应该具体对待.本文中介绍与前面不一样的规律探索方法:直接从问题的一般情况出发,得出一般规律;或在计算多个几何量(或多个数)之和时,不分别计算每个变量的具体值,而只求出由这些变量构成的某个代数式的整体值.这种从一般情况分析、或从整体分析处理问题的方法,使问题解决更合理、更简洁且实用.
2 求点的坐标
例1(德阳中考)如图1,在平面直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1,P2,P3,……,Pn,使OP1=1,P1P2=3,P2P3=5,……,Pn-1Pn=2n-1(n为正整数),分别过点P1,P2,P3,……,Pn向射线OA作垂线段,垂足分别为Q1,Q2,Q3,……,Qn,则点Qn的坐标为.
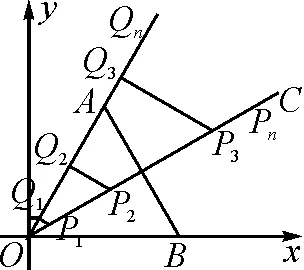
图1
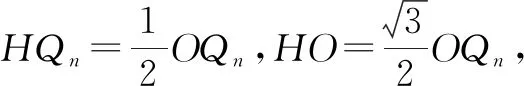

图2
下面只需解决OQn与OPn的关系.
在Rt△OPnQn中,由∠QnOPn=30°,可得


点评:规律探究问题通常由特殊到一般,由具体到抽象,找出几个特殊情况,再去类比、猜想、分析一般的规律特征.本题若按部就班,则涉及的点太多,关系过于复杂.因此,反其道而行之,直接去求点Qn的坐标.利用含30°角的直角三角形的性质,寻找Qn的横纵坐标与OQn的关系,进一步寻找OQn与OPn的关系即可解决.同时,求OPn运用整体思想解决显得浑然天成、精彩灵动.
3 求线段和
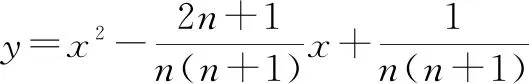
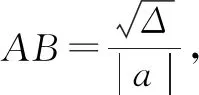
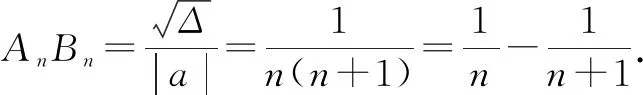
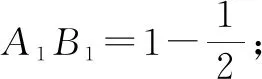
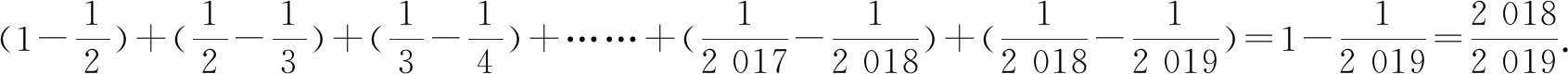
因此选:C.
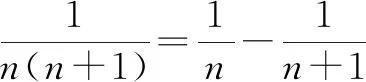
进一步拓展:原题已知条件不变,把所求结论部分改成“求A1B1+A2B2+A3B3+……+AnBn的值”.
4 求与反比例函数有关的三角形面积之和

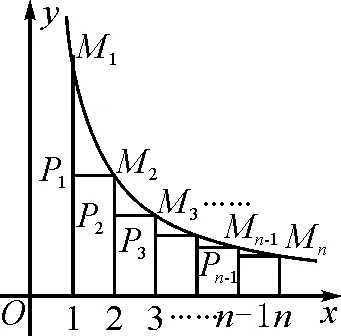
图3
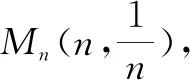
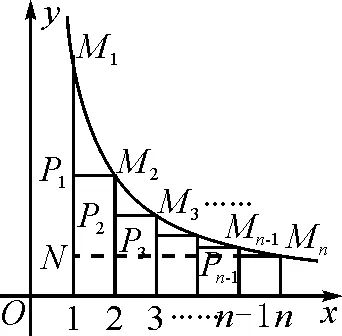
图4
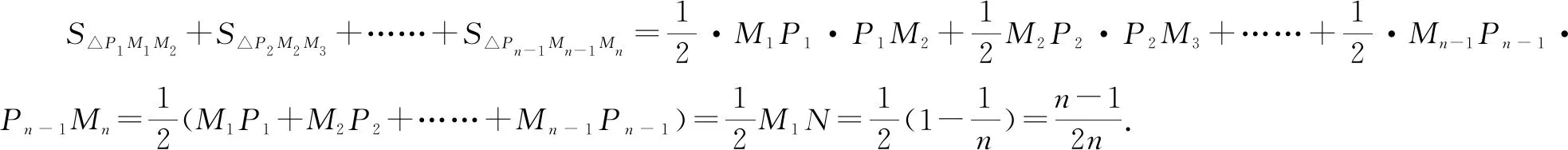
点评:本题若将所求三角形的面积一个一个算出来,再去寻找规律,过程会显得繁琐而冗长;而利用每个三角形的底边为1及反比例函数图象上点的特征,再运用平移及整体思想,将分散的线段平移到同一条线段上,则可快速解题,化困难为神奇,不得不拍手称快.
5 教学启示
《义务教育数学课程标准》提出,数学学习不仅包括数学的一些现成结果,还包括这些结果的形成过程.规律探索性问题,正是新课程理念下培养学生观察、实验、操作、归纳、猜想,发展学生的直觉思维和合情推理能力的绝好材料.它不仅可以考查学生发现问题、自主探究、解决问题等综合能力,暴露学生在解题过程中的思维品质,还能反馈学生对数学思想方法的掌握情况,较直观地反映出学生的数学素养,体现出新时期下数学课程的基本要求.
探索性问题的素材包罗万象,一切都可入题;题型之多彩,设计之巧妙,相对于传统试题来说是一种突破,是一种创新.规律探索是发现数学知识的一种创造性思维,也是探索发现新知识的一种重要手段,一般按照“问题—猜想—验证—总结—结论”的流程进行解题.在平时的学习中,我们不但要探讨此类问题的一般解法,也要有意识地甄选出别样解法的试题进行对比训练.这样学生便可以灵活运用解题方法,从整体上把握题目,创造性地分析解答问题,不仅有助于形成整体性的思维方式,而且更能够让学生在解题过程中发现数学的无穷魅力.
当然以上各题不用整体思想也可以求出,只是过程更长一点,运用整体思想解题则体现出创造性解决问题的能力,是求简意识的体现.因此,在平时训练时,我们不仅要思考怎样去分析题意、探索解题思路,更重要的是思考怎样才是最简的,其解法又是怎样想到的.这里的核心,不是从一题多解的基础上找出一个最优解,因为这样做太浪费时间和精力,而是培养学生从一开始就能较为迅速地寻求和发现解决问题的最优路径的意识和能力,或者说帮助学生如何去制定出最佳的解决方案,这是我们在习题教学中要努力实现的目标.正如高斯所说,“去寻求一种最美和最简捷的证明,乃是吸引我去研究数学的主要动力”.也正是这种动力,才能从更高层次上去激发学生学习数学的兴趣,进而培养创新精神和探究能力.

