基于聚类算法的变压设备运行数据监测与异常检测技术
杜 涛,王朝龙,朱 靖,赵健勃,马 麒,刘勃君
(1.国网青海省电力公司 西宁供电公司,青海 西宁 813000;2.国网青海省电力公司,青海 西宁 813000; 3.国网青海省电力公司 信息通信公司,青海 西宁 813000;4.上海迈内能源科技有限公司,上海 200000)
因变压设备在线监测数据具有类型繁多、体量大等特点,引用大数据技术开展在线监测数据异常检测过程中,便于深入挖掘在线监测数据中的异常信息。近些年,大数据技术在互联网、物流等多个领域得到广泛的应用,展现出较高的应用价值。对电力设备进行异常检测过程中,引入大数据技术能够为设备异常检测准确性提供新的解决思路和方法,便于及时解决传统阈值方式难以轻易提取故障预警特征的不足之处。为有效解决变电站变压设备在线监测多元数据开展异常检测,文中提出一种基于k-means聚类算法创建多元特征量数据点中的异常检测模型,便于及时检出异常点,确保电力系统稳定的运行。
1 变压设备异常常用的诊断方式
在电力系统各类电气设备内,变压器是电力系统重要的枢纽设备,其能够正常的运行是确保电力系统安全工作的关键。因变压器长时间连续的运行,不可避免的会出现一系列故障。加之,变压器结构比较复杂,出现异常均会引发多种故障,一种异常也会在不同程度上出现多种故障状态。基于此,设法减少、预防变压器出现故障,确保变压器正常的运行,成为电力企业迫切需要解决的问题。外观检查、高压电气实验等均是收集变压器状态信息常用的检测方法,上述方式所获取的信息比较滞后。所谓滞后信息,就是变压器出现故障或者事故后获取的状态信息。检测变压器异常传统方式多种多样,但上述方式难以掌握变压器实时状态信息,无法达到设备状态维护现代化发展需求。为解决传统收集方式存在的不足之处,越来越多的学者开始进行变压器状态监测,即对变压器开展实时、全面的状态监测工作。为避免故障对变压器带来不良的影响,需要全面了解变压器内部绝缘情况,也就要求通过变压器在线监测及异常诊断实现。如果能够及早发现变压器出现的异常情况,有利于减少变压器维护费用,对于延长变压器使用寿命、提高经济效益具有重要的意义。而对变压器异常情况诊断时,传统推理诊断方式无法准确展现复杂系统的本质特性。油中溶解气体分析(DGA)作为变压器异常诊断的主要方法,大型变压器均通过油进行绝缘和散热,实际运行中,变压器内部绝缘油与油内有机绝缘材料受到放电等因素的影响慢慢老化、分解,出现少量一氧化碳等气体。DGA是指依托分析油中溶解气体组分比值及其含量对变压器异常状况展开诊断的方式,在电力系统中得到广泛的使用[1-2]。常规DGA方式包含IEC比值法、无编码比值法、特征气体法等。由于传统异常状况诊断方法诊断准确率不高,这是因传统诊断方式诊断结果准确度依赖经验积累而来。变压器发生异常是由某一异常情况引发多个异常导致的突发性故障,因此,传统诊断方式无法达到模糊性、复杂场合要求。随着模糊理论、K-means聚类算法等理论的发展,通过大数据技术开展变压器异常诊断获得良好的效果。随着不同智能方式的应用,只采用一种智能方式对变压器异常进行诊断存在一定的局限性,把2种或多种智能方式联合起来开展异常诊断成为其发展的必然趋势。
2 设计变压设备异常检测模型
2.1 基于滑动窗口候选异常数据集
时间序列X代表通过记录时间、记录值构成的元素有序集合,X={(t0,x0),(t1,x1)…,(ti,xi)…}。假定实际运行阶段数据点X与Z相关,这种假设情况下,变压器实时运行阶段状态量随着时间量的动态改变,且满足实际序列特性。正常条件下,如果时间Z取值比较近,X并未出现较大的改变,均匀分布于当前时间窗中全部X值中的平均值avg(X)附近。如果某一个数据点Q中的X数值与avg(X)发生明显的偏离,Q点出现异常的可能性比较大。基于此,文中依托固定长度条件下滑动时间窗口对时间序列局部数段开展阈值判定,并对数据流实施预处理及其异常模式评估。
本次研究定义Sw[t-w:t]当做数据流时间间隔(w)的滑动窗口,t、w单位相同,t>w。这一滑动窗口中相应的数据点代表为Sw(xt(w))={xt-w,xt-w+1…,xt-1,xi}。挑选有待识别的数据点Q作为t时刻的xt,具体评估异常模式操作:

(2)求解滑动窗口内至数据点空间中心这一阶段的平均距离:
(1)
式中:d(xt)为t这一时间段数据点xt至数据点空间中心之间的距离。
(3)求解得出:zt=|d(xt)-d(xt-1)|:
(2)
进一步求解预测出处于均值周围xt数值:
(3)

重复上述步骤,直至整个时间序列筛选完成为止,获得存在候选异常数据集D。
通过上述分析可知,滑动窗口筛选候选异常数值算法受阈值τ、时间窗宽度w这2项参数的影响。为确保实验结果,挑选阈值应根据实验及其工程实验得到最佳值,依托500多组变压器异常数据点结果设置候选异常数据的阈值,综合分析全部的异常数据发现,τ取值为0.13。与此同时,本次研究使用异常数据检测准确率a,进一步判定滑动窗口的w对最终异常监测结果产生的影响,计算公式为:
(4)
式中:Noutlier代表最终检测出来的异常数据量;NT表示有待检测数据中存在异常的总数量,实验结果如图1所示。由图1可知,由于w数值不断增大,检测准确率随之上升;若w≥8后,检测结果准确率慢慢趋向稳定。分析发现,如果滑动窗口宽度比较小,数据点X邻近具有较少的数据点,无法依托历史数据展开有效的阈值判定。由于w值增多,数据流包含大量的状态信息,使得算法检测准确性趋于稳定。这种情况下,从算法时间及其空间成本分析,文中设定w=8。

图1 滑动时间窗口宽度影响检测准确率Fig.1 Sliding time window width affects detection accuracy
2.2 基于K-means聚类算法异常数据检测
K-means聚类算法作为一种迭代求解算法,其操作在于随机挑选K个对象当做初始的聚类中心,随之,求解每一个对象与不同种子聚类中心的聚类,将每一个对象分配至距离最近的聚类中心[3-4]。K-means聚类算法是依托划分的聚类算法,尝试找到促使平方误差函数最小的k个划分。如果簇与簇之间存在明显的特征区别,且结果簇比较密集,K-means聚类算法得到的结果最好。K-means聚类算法优点如下:K-means聚类算法操作简单、快速;K-means聚类算法对于挖掘大数据集效率较高,且展现出可伸缩性的特点[5-6]。
聚类分析就是在不知情条件下进行类型划分,选取相似度当做量化标准,对变压器运行情况展开评估[7-8]。这一评估操作依托求解不同类之间的相似度,按照相似度具体排名,对设备运行状况进行分析。本次研究所选K-means聚类算法,依据最小的相似度进行数据分析,对不同数据之间的关系实施简化处理,在一定程度上减轻数据分析工作量。
假定集合U的数据点数量是N,空间维度用M代表,对这一集合实施拆分处理,分为k个子集以此组成K-聚类,每一个聚类包含1个簇,求解N个聚类簇的平均数值。采用建立聚类目标函数,对其质量进行评估,公式为:
(5)
式中:G代表有待检测对象所处位置相对聚类中心之间的距离和;dij(xj,cj)表示聚类中心与待检测对象间的欧式距离。数据检测对象紧密度会随G的减小更为紧密。在G值处于最小的状态,聚类中心最好。
本次开展异常数据检测模型构建过程中,挑选环境温度、负荷等指标当做集合维度指标,向着K-means聚类中心输入500多组数据,获得相应的聚类簇数量,用k代表。假定阈值是P、k聚类簇中心与上述维度指标间的距离超过P值,判定这一数组未出现在簇内。因此,使用本模型检测异常数据,可查看不同维度数据点与簇中心间的距离情况实施判断,获得设备是否出现异常的检测结果。
3 变压器运行状态检测操作步骤
3.1 数据预处理分析
对变压器运行状态进行检测时,必须根据不同标准展开判断,极易发生阈值过小容易忽略的情况。因此,必须对数据采取特征开展预处理,从而提升数据的鲁棒性。开展数据预处理时,涉及平均绝对偏差等方面的计算,求解公式为:
1)平均绝对偏差
(6)

2)特征属性值
求解公式:
(7)
3.2 异常状态分析步骤
待检测设备数据属性值给予预处理后,遵循下列步骤开展检测:(1)利用K-聚类数据划分方式把历史数据分成n个聚类簇,明确各聚类簇中心;(2)根据获取的在线监测数据筛选相应的异常数据,这一环节把数据分成多个时间序列,自序列内找到相应的异常数据。对异常数据进行标记,把筛选的数据纳入集合D内;(3)遵循聚类簇判定标准,依据包含关系,对D内数据点实施判断,若数据点不包括聚类簇集合,认定这一数据是状态异常数据点;(4)选取上述3步判断结果为依据,查看异常数据点相邻条件下数据点所属状况,获取多元时间序列数据异常结果。
4 应用实例分析
为进一步检验这种算法对于多元时间序列出现异常情况检测的有效性,选取变压器为对象,对其在线监测数据出现异常情况实施检测。一般先把对负荷影响较大的因素考虑在内,对电力负荷产生影响的各项因素,温度上升、下降对负荷改变产生重要的影响。而开展异常数据监测有利于其判定噪声数据,改善传感器传统阈值判定方面的问题。本次研究将负荷、环境温度、甲烷(CH4)及其乙炔(C2H2)气体考虑在内,判断其对于变压器故障产生的影响。选用某变电站一台主变压器为对象,以2020年6月500多组负荷、环境温度、CH4等指标在线监测历史数据,当做训练样本开展正常的数据聚类。并选取2020年7月6日00:00G至2020年7月7日01:00这一时间段的数据,共有25 h,每隔5 min作为相应的时间间隔(有300个时间间隔),以这段时间的数据当做异常检测样本。
对500多组历史在线监测数据展开分析,正确聚类簇数量k、阈值P选定对最终异常数据监测产生重要的影响。基于此,对聚类簇k,考虑温度类型根据时间的周期性展开操作,按照正常数据类型取值k=3。对于出现异常数据的判定阈值P,根据已经聚类的正常簇类中心至其簇正常部位的最大距离值,其检测正确率结果如表1所示。最终根据稳定下来的数值,选定D=(r1,r2,r3)=(0.7,0.8,0.78)。
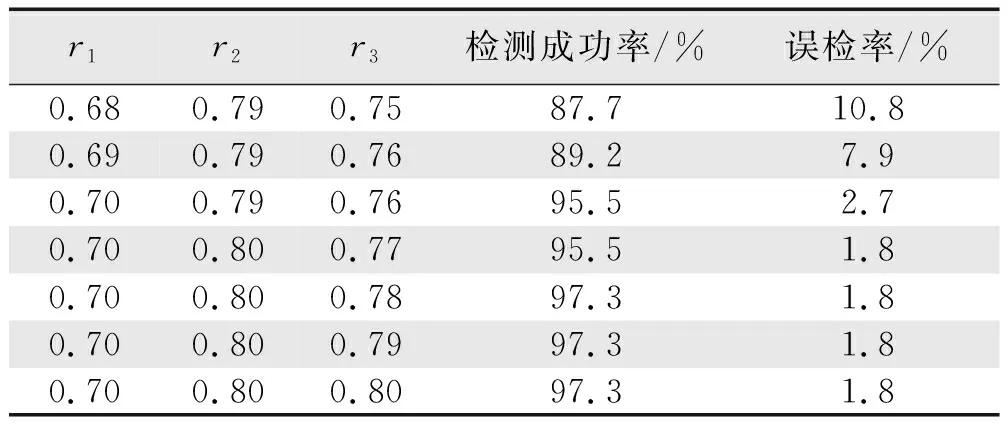
表1 所选阈值对异常检测数据的影响Tab.1 Influence of selected thresholds on anomaly detection data
对由表1可知,对所选300组待检测数据选出相应的异常数据集,判定候选异常数据集每一个时间点的数据是否在3个正常簇内,如果不属于,则判定为异常数据点。分析结果可知,在0~300这一范围的数据流内,大致划分为3类数据:
(1)当T处于100~110,出现一小片连续的异常数据点,说明变压器在这一阶段发生不稳定的异常运行情况,需要对设备健康状况展开进一步的评估;(2)当T=240后,发现这一连续时间段之内多数数据不属于任何一个正常的簇类,得到下列结论:设备在这一时刻后出现可能的故障预兆,需要尽快对相关模块设备状况进行评估;(3)当数据处在某些时刻(例如:T=50、T=200)的数据点不隶属于3个聚类簇,但其邻近时刻数据点显示为正常数据,可知这一时刻出现明显的异常点数据噪声。分析其原因发现,因某个传感器不稳定引起的,可予以忽略。分析实际情况发现,处在2020年7月6日08:15(T=87)这一时刻,受到天气因素的影响,变压器受到短暂的雷击发生放电,使得C2H2数值短时间内快速升高,CH4数值略微上升。这个变压器在2020年7月6日21:40(T=237)出现超预定值运行的情况,负荷慢慢升高,随着顶层油温逐渐升高及油内CH4含量略微上升。通过深入分析这一变压器异常状况与实际运行状况相符合,提示变压器异常运行情况会随着多种状态量发生改变,选取单一特征值阈值判断方式无法及时检出异常情况,极易受到噪声的影响。而本文所用方法对变压器异常状态实施检测展现出实效性、有效性等特点,可根据在线监测的数据流内迅速检出异常情况,及时消除传统阈值检测方式中因噪声数据引起的误判情况,具有较高的应用价值。
5 结语
针对变压器传统检测方法的不足之处,本文中围绕变压器异常状态数据展开分析,建立相应的检测模型,依托分析异常多元数据点相邻时间段之内存在异常数据点数量,评估设备运行状况。研究结果说明,所用模型不仅能准确检出变压器出现的异常数据点,也达到数据检测实时性方面的要求。

