融合径向基神经网络和遗传算法的翻板钢水闸门优化

贺弘扬

(杨凌职业技术学院，陕西 西安 712100)

闸门是水利工程的核心节点之一。其通过控制孔口的出水量来控制河流上下游的水位，从而达到水运通航、农业灌溉、防洪削峰等目的，造福国民[1]。闸门中运用较多的类型是翻板钢水闸门，它是通过调节闸门在河流横截面上受力的力矩来实现闸门开启关闭的。相对于传统水闸门，其含有多种优点，如工程造价低廉、维修保养方便、水位控制更精准等。所以翻板钢水闸门的应用前景十分广阔[2-5]。但因其结构特性，耗钢量较大，因此应用现有的先进知识对其进行理论分析和结构优化，有一定的实际经济价值[6-8]。

1 融合径向基神经网络和遗传算法的翻板钢水闸门优化设计

1.1 构建翻板钢水闸门的有限元计算模型

该研究选取国内某翻板钢水闸门项目为样本，水闸门坝长85 m，有16扇，3孔结构，其单扇门长5 m，高2 m，各扇门的主要承力结构为轻型工字钢100制成的主梁、轻型槽钢100制成的次梁、不等边角钢(L75×50×10)制成的斜梁；另外，其面板由1 cm厚度的钢板制成，具体结构如图1所示。

图1 翻板钢水闸门样本平面图Fig.1 Sample plan of flap steel sluice gate

该闸门结构主要分为面板铆接、梁格焊接构成后对接闸门的橡胶袋组，梁格是用于支撑面板的主要结构[9]。根据上述关于实体样本翻板钢水闸门结构和尺寸材料参数，采用ANSYS软件构建其有限元模型，为后续研究和计算使用。

(1)给该翻板钢水闸门模型选择合适的各结构建模材料，因为该水闸门梁格的主梁、次梁、斜梁均为钢结构，我国现行的钢闸门设计规范里要求闸门结构的等效应力即便在极端情况下也不能超过对应的容许应力值[10-14]。所以为其选择密度7 800 kg/m3、弹性模量2.06×1011Pa、泊松比0.3的Q235钢材。根据《水利水电工程钢闸门设计规范》(SL 74—2013)得到Q235钢材的各相关容许应力与破坏强度，抗拉压、抗剪、局部承压、局部紧接承压容许应力分别为[σ]=160 MPa、[τ]=95 MPa、[σcd]=240 MPa、[σcj]=120 MPa，钢材屈服强度[σs]=235 MPa；

(2)翻板钢水闸门的各基本结构选择合适的有限元模型单元，根据水闸门的力学结构，研究决定主要采用有限元建模软件ANSYS中的板单元、梁单元来进行模拟[15-19]。主梁、次梁、斜梁3结构做空间梁单元模拟，门叶结构划分为多个薄板单元进行模拟。板壳单元需要承受平行板壳方向与垂直于板壳方向的荷载与弯曲变形、薄膜变形[20]。所以，该单元的各节均含有6自由度，其为与3坐标轴方向平行的位移自由度和绕3坐标轴旋转的转角自由度。综上分析，该翻板钢水闸门的闸门面板结构应采用4节点的SHELL63矩形单元模拟。模拟各种梁结构时，ANSYS中的Beam4、Beam188单元都符合要求；然而Beam4单元建模时还需进行节点耦合操作，这在对复杂钢闸门结构建模时会消耗更多时间精力，相比之下，Beam188单元建模更为简单；因此采用后者模拟各种梁单元。确定对应的有限元模拟单元后，根据材料的相关特性对各单元进行单元属性定义，使得模型单元与实际工程单元具有相同的物理性质；

(3)对模型进行网格划分，划分是否合理，会对计算结果产生巨大影响。然而网格划分越细致，虽计算结果与实际情况更接近，误差也越小，但对计算机配置要求也更高，容易导致计算速度过慢。因此综合考虑计算速度与计算精确性、能否描述出模型的基本细节等，限制每个单元各边长最大不超过50 mm，从而将闸门的ANSYS模型切分成4 421个节点与5 166个单元；其中板、梁单元各有4 293个、873个；

(4)设置模型受到的荷载，对水闸门进行受力分析可知，其受到的荷载分为方向与面板垂直的水压荷载、作用于各支撑节点的约束荷载，还有模型自身受到的重力；但考虑到水闸门在荷载最为不利的闸门满水状态下处于竖直形态，其自重不会影响到闸门框架的内力，所以该研究不考虑闸门自重，仅对模型添加前2种荷载。

1.2 融合径向基神经网络和遗传算法的改进混合算法设计

为同时实现节省翻板钢水闸门工程的修建材料，特别是钢材消耗量和保证结构安全性的优化目标。需要借助径向基(RBF)神经网络的最优逼近与遗传算法(GA)良好的全局寻优性能，设计出融合遗传算法和径向基神经网络响应面的混合算法。

RBF网络为一种具有单隐层的3层前馈网络，能以任意精度逼近任意非线性映射关系，对输入特征的响应准确率较高。其结构与BP网络相似，神经元结构如图2所示。

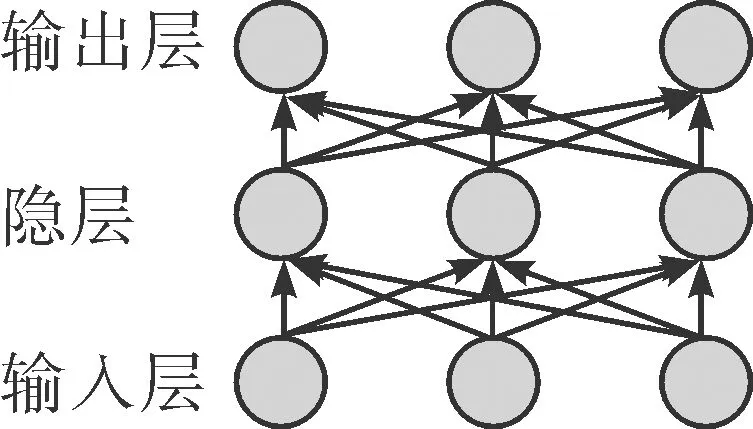
图2 RBF网络的结构示意图Fig.2 Structure diagram of RBF network

从图2可以看出，其网络的第1层为数据输入层；第2层为隐含层，该层神经元数量与输入数据的特征复杂度密切相关，下一层为输出层，用于将上层输入信号组合映射成所需形式再输出。RBF神经网络通过径向基函数及其相关神经元结构组成了隐含层空间，将数据映射到该隐层空间，对于此种神经网络，一旦各层神经元个数及连接关系、相关函数等参数给定，RBF神经网络就能开始高效迭代学习，并且快速训练完成网络，这就是RBF网络对解决包含自适应在内的控制类型任务具有优势的原因。而确定隐层神经元参数则大多数情况下需要采用非线性策略完成，其必须提前设置网络中心数量等参数，才能实现数据的非线性映射。

有限元计算需要耗费大量计算机资源和计算耗时，特别是对复杂模型计算，若针对本结构每一个可能的最优化方案都进行有限元计算，效率过于低下；所以，为了提高该研究的优化效率，融合径向基神经网络和遗传算法构建混合优化算法。该混合算法具体的流程如图3所示。

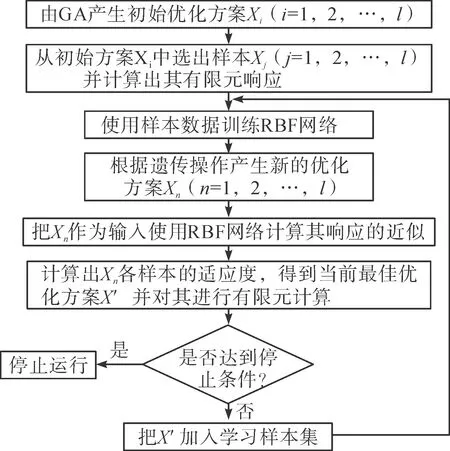
图3 融合RBF网络和GA的混合优化算法流程图Fig.3 Flow chart of hybrid optimization algorithm integrating RBF network and GA

从图3可以看出，其构建思路：使用遗传算法前期运行阶段生成的可行解中的一小部分作为算法输入数据，运用ANSYS计算出每组方案的应力应变数据，作为标签，形成适合有监督学习使用的完整数据组，将其输入RBF网络，至此形成闸门核心结构尺寸参数到受力状态下的应力应变映射系统。严格来说，输出只是实际数据的近似，这样做是想通过牺牲一定程度可以忍受的计算精度来换取更高的优化效率，而且为了减少误差，在每代遗传中，都会在数据集中加入一个遗传优化出的当前最优解，及其有限元计算结果。

2 改进混合算法的翻板钢水闸门优化结果分析

使用MATLAB编写脚本实现混合模型，运行混合模型输出闸门的设计变量即各结构的优化后几何尺寸，以充分发挥材料的性能，在满足应力应变要求的前提下，节省材料用量。设置遗传算法部分的种群规模为40，且为了提高RBF网络的输出精度，再向遗传算法40个初始样本中插入20组均匀的优化方案，则共得到60组优化方案。将闸门结构中各梁的截面惯性矩、神经网络训练后输出的各梁等效应力变形设置为影响因子，同时再将混合算法的训练终止条件设置为均方误差小于0.01，模型的训练误差下降过程如图4所示。

图4 模型训练误差下降过程Fig.4 Process diagram of model training error reduction

从图4可以看出，GA算法虽然比混合RBF网络算法更快收敛，但是其收敛效果更差；后者收敛时训练误差为0.018，比前者0.250减小了92.80%。为了检验混合算法的预测精度，取遗传算法第1代产生的所有样本作为测试样本输入RBF网络，得到预测出的应力应变值，再与其经过ANSYS计算出的应力应变数值对比，统计误差结果如图5所示。

图5 混合算法响应误差测试结果Fig.5 Response error test results of hybrid algorithm

从图5可以看出，应力应变的误差都在0附近波动，误差的平均值分别为0.024 7 MPa和-0.003 35 mm，说明该混合优化模型的误差是随机分布的，并没有系统性误差。这40组方案的大部分应力误差绝对值都小于0.5 MPa，最大值为0.582 MPa，大部分方案的应变误差绝对值都小于0.1 mm，最大应变为0.163 mm。测试数据证明，该混合优化模型的误差小，精度足够，可以用来预测翻板钢水闸门的应力应变数值。然后运行该模型对闸门各部件的几何尺寸进行优化，模型迭代到第42次时均方误差低于0.01，算法收敛完成。整理优化出的部件尺寸与原设计尺寸，统计结果如表1所示。

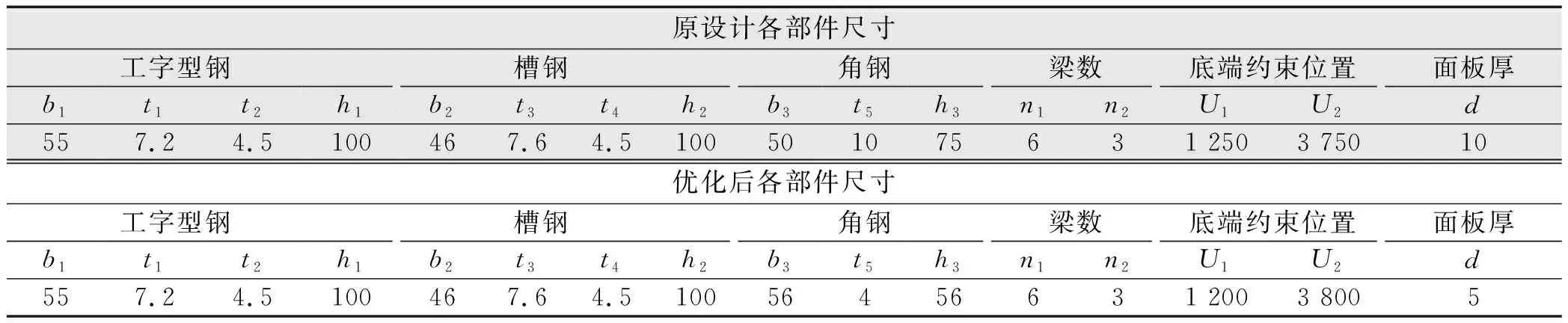
表1 原设计与优化后方案的各部件尺寸Tab.1 Dimensions of components in original design and optimized scheme mm

由表1可知，优化前后工字型钢、槽钢的型号完全不变，其截面积分别为12.0、10.9 cm2，还有梁的数量与配置也完全不变。但角钢和面板厚度尺寸有明显变化，角钢从不等边75 mm×50 mm×10 mm角钢，换为等边45×45×5角钢，截面积减小为4.29 cm2。面板厚度从10 mm减少到5 mm，最后是底端约束位置略有调整U1从1 250 mm减少为1 200 mm，U2从3 750 mm增加为3 800 mm。将2组方案分别使用ANSYS软件计算，发现优化后最大应力从142 MPa增大到162 MPa，虽然有所增加；但仍然大幅小于容许应力值。同时，最大位移从4.66增大为4.92 mm，同样远小于水闸门设计规范中规定的最大值Umax=L/600=5 000/600=8.3 mm(L为单扇门的长度)，也满足规范要求。优化后的翻板钢水闸门总耗钢量为0.105 1 m3,相比于原设计方案的0.156 7 m3节约了32.93%的钢材，优化后的经济效益显著。

3 结语

针对翻板钢水闸门的结构优化问题，研究选择国内某翻板钢水闸门为案例，根据其结构和材料信息并查询相关行业规范标准，运用ANSYS软件构建出能模拟出其力学状态的合理有限元模型；然后，融合径向基神经网络和遗传算法组成混合优化算法，使用遗传算法产生的部件尺寸方案作为输入数据，输入径向基网络预测出该方案的应力应变响应数据，可在控制响应计算精度和优化部件方案的前提下，大幅提高优化方案的计算效率。采用MATLAB软件实现混合优化算法，对比原设计方案和优化后方案，发现工字型钢、槽钢的型号、梁的数量与配置完全不变，角钢从不等边75×50×10，换为等边45×45×5型号；面板厚度从10 mm减少到5 mm；优化后方案最大应力从142 MPa增大到162 MPa；最大位移从4.66增大为4.92 mm。但都远小于规范规定的容许值，同时优化后水闸门总耗钢量为0.105 1 m3,相比于原设计方案的0.156 7 m3节约了32.93%的钢材，优化后的方案经济效益显著。