基于特征融合的注意力增强卷积神经网络的航空发动机滚动轴承故障诊断方法

李泽东， 李志农， 陶俊勇， 毛清华， 张旭辉

(1.南昌航空大学 无损检测教育部重点实验室， 江西 南昌 330063；2.国防科技大学 装备综合保障技术重点实验室， 湖南 长沙 410073；3.陕西省矿山机电装备智能监测重点实验室， 陕西 西安 710054)

0 引言

滚动轴承作为航空发动机的关键部件，通常处于高转速、大噪声环境下，极易产生故障，从而影响发动机正常有效的工作。因此，有必要研究高转速下航空发动机滚动轴承的故障诊断方法。

近年来，基于深度学习的滚动轴承智能诊断方法取得了很大进展。其基本思路是提取振动信号的时频特征、灰度图等，然后，输入到深度学习网络中进行故障识别[1-5]。例如，文献[1]中先将轴承振动信号通过傅里叶变换预处理为频谱图，然后将频谱图作输入到深度卷积神经网络中进行轴承故障诊断。文献[2]将轴承振动信号预处理为时频图，再将时频图作为深度卷积神经网络的输入以识别不同类型的轴承故障。文献[3]中将振动信号转换为灰度图像，再结合深度卷积神经网络诊断轴承不同类型的故障。文献[4]中利用连续小波变换对轴承的原始振动信号处理为时频图，再结合深度卷积神经网络识别不同故障。文献[5]中结合红外热图像和深度卷积神经网络对轴承进行故障诊断。还有以端到端的方式直接对振动信号进行训练从而进行故障诊断[6-10]。文献[6-10]中均将轴承的原始振动信号直接作为深度卷积神经网络的输入，形成了端到端的故障诊断。这些方法都是建立在深度卷积神经网络中卷积层可以自适应地提取信号特征的基础上[11]。然而，深度卷积神经网络中的卷积层在对输入进行卷积运算时，主要针对局部感受野提取信息，容易忽略全局信息。考虑到注意力机制是一种可以捕捉全局感受野捕捉的方法，通过对不同特征赋予不同权重，以提取更加有用的局部信息[12]。目前，一些结合注意力机制和深度卷积神经网络的方法已经被应用到故障诊断中。文献[13-14]将轴承故障振动信号转换为时频图后，输入到深度卷积神经网络中，利用注意力机制进行融合图像的多通道信息，进行故障识别。文献[15]通过构建多尺度的卷积神经网络对信号进行训练，利用注意力机制对多尺度卷积神经网络进行融合，实现轴承的故障诊断。文献[16]提出一种特征注意力机制，考虑了故障信号时间尺度的干扰，从而进行滚动轴承的故障诊断。然而，上述关于注意力机制与深度卷积神经网络的结合是将两个孤立部分机械式地结合，注意力机制要么在深度卷积神经网络之前，要么在深度卷积神经网络之后，注意力机制中的参数未参与到整个神经网络的训练中。很显然，这种注意力机制与深度卷积神经网络的结合，若注意力机制中的参数选择不恰当，往往得不到满意的故障识别效果。因此，有必要探讨新的注意力机制卷积神经网络以克服此不足。

基于此，本文提出一种基于注意力增强卷积神经网络(AACNN)的机械故障诊断方法。相对传统的注意力卷积神经网络，所提方法将注意力机制和卷积层结合构造了注意力增强卷积层，使得注意力参数和卷积参数在整个网络中进行正向传播和反向调优。然后，将所提方法应用到航空发动机滚动轴承故障诊断中，并与传统的注意力卷积神经网络进行对比研究，以验证构建的AACNN有效性。

1 面向故障诊断的AACNN构建

传统卷积神经网络的卷积运算主要针对局部感受野进行的，因此，在提取特征时会失去一些全局信息。而注意力机制具有捕获远程交互的作用，可以更好地关注全局信息。因此，将注意力机制和卷积运算融合起来构造了一种注意力增强卷积运算。该运算可以通过注意力机制将输入经卷积后的映射图进行级联来提取和融合特征，并且将注意力机制贯穿整个神经网络模型。AACNN中使用多头注意力机制与卷积融合构造注意力增强卷积层，使模型对数据在高维空间和特征子空间中进行融合，具体过程如下。

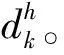
(1)

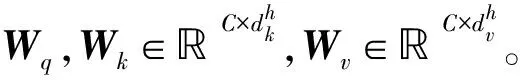
MHA(X)=Concat[O1,…,ONh]WO

(2)

式中：Concat[]表示将每个单头的输出串联到一起；Wo表示线性变换矩阵，Wo∈dv×dv。

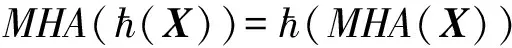
(3)

(4)

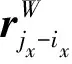
(5)

注意力增强卷积采用多头注意力机制共同构建原始空间，每一个头都对应自己的特征子空间。同时，将卷积操作加入对局部特征提取，所得注意力增强卷积可以更容易地对不同空间维度的输入X进行操作，其输出XAA为

XAA=Concat[Conv(X),MHA(X)]

(6)

式中：Conv(·) 为标准卷积运算。

输入通过注意力增强卷积层提取融合特征后，接下来需要进行标准的卷积运算。对于经过注意力增强卷积层后的输出XAA，通过卷积核继续计算其不同的特征，具体的卷积过程为

(7)

卷积层之后通常是池化层，用于对经过卷积操作后得到的高维输出的降维，池化的具体计算为

(8)

池化的方式通常有最大池化和平均池化等。经过卷积和池化后，通常会对池化后的输出进行铺平操作，再通过全连接层进行连接，最后进行分类输出。

(9)

(10)

(11)

在模型的训练反向传播中，以(12)式所示的交叉熵损失函数，作为模型的损失函数，用于衡量模型输出yo与真实输出y之间的误差。对模型进行反向求导，训练的目标就是使输出值与真实值尽可能地接近。

loss=-(ylg (yo)+(1-yo)lg (1-y))

(12)

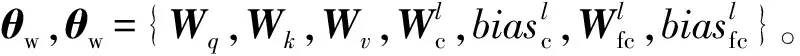
(13)

式中：L(fθ(θw;X,y))为每次迭代中所有样本的损失；m为总样本数。

为了加快寻找最优值的速度，利用Adam优化器对损失函数进行优化，具体过程如下：

在每次迭代t(t=1，2，…，N，N为最大迭代次数)中，对θw求梯度gt，得

(14)

式中：“:=”表示更新运算。

计算1阶矩估计mt和2阶矩估计vt，可得

mt=β1mt-1+(1-β1)gt

(15)

(16)

式中：β1为控制动量与当前梯度的指数衰减率；β2为控制之前梯度的平方影响情况的指数衰减率。为防止mt和vt在初始化时偏向0，采用(17)式和(18)式对其进行纠正：

(17)

(18)

对参数集θw进行更新，可得

(19)

式中：η为学习率；ε为避免除数为0的修正项。

2 AACNN故障诊断流程

基于AACNN进行滚动轴承故障定性诊断时，分为信号采集与样本划分、样本信号特征模量提取、数据集构建、AACNN设计与训练、航空发动机滚动轴承故障诊断5个步骤，流程如图1所示。图1中head1和head2为注意力机制操作的输出对象。

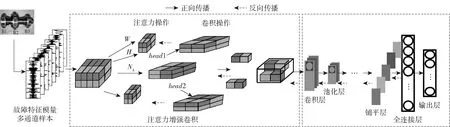
图1 面向故障诊断的AACNNFig.1 Fault diagnosis model based on AACNN

具体步骤如下：

1)信号采集与样本划分：通过加速度传感器采集滚动轴承的振动信号，利用等长的窗口进行划分，得到信号的样本。为了对数据增强处理，采用重叠切片方法，即划分样本的窗口长度小于单个样本信号。

2)样本信号特征模量提取：在高转速、大噪声条件下，滚动轴承的振动信号非线性、非平稳性较强。因此，通过信号处理的方式，如经验模态分解(EMD)、变分模态分解(VMD)和小波包分解(WPD)等，将原始振动信号分解成不同尺度的特征模量。

3)数据集构建：将上述特征模量按顺序堆叠成一个多通道样本，将所有样本进行同样的操作构造多通道样本数据集。创建好多通道数据集后，将数据集划分为训练集和测试集。

4)AACNN设计与训练：AACNN的性能与卷积层的数量和大小密切相关。其中卷积核尺寸大小需要根据一些基本的设计来确定，相对小卷积核来说，大卷积核可以提高感受野。但是AACNN中包含注意力增强卷积层，它可以通过多头注意力机制关注全局感受野。因此，AACNN具有强大的自适应提取和融合特征的能力。在设计时，注意力增强卷积层的注意力机制头数目等于输入多通道特征模量数。其余卷积层采用小尺寸的卷积核，目的是加深网络，从而更好地学习特征，提高网络的表达能力。

按照上述原则建立AACNN模型，通过反复实验调整参数，模型具体参数如表1所示。为防止模型过拟合，在模型中加入Dropout，它将网络中的神经元以一定的概率置为0，以提高网络的泛化能力。用构建好的训练集进行训练，调试超参数，获得性能较好的AACNN模型。

5)航空发动机滚动轴承故障诊断：利用测试集验证AACNN模型故障诊断的有效性，并使用10-fold交叉验证方式来评估模型的性能。为了验证模型的泛化能力，通过不同信噪比的信号来测试模型。

本文所提方法通过信号处理的方式对高转速下的滚动轴承振动信号提取特征模量，利用AACNN对特征模量按一定权重进行自适应特征融合和选择，更好地适用于高转速下的滚动轴承故障诊断。

表1 AACNN模型结构参数Table 1 Parameters of the AACNN model

3 实验验证

3.1 实验数据描述

实验数据来源于高速环境下航空发动机滚动轴承测试台[18]，如图2所示。实验台上包含一个带有3个轴承的高速主轴(见图3)，一套动力系统，润滑器和两个加速度传感器等。动力系统通过一个滑架为轴承加载，润滑系统通过油脂润滑的方式为轴承润滑，主轴的速度是通过变频器的控制面板设置的。主轴安装时，在两个相同的滚柱轴承外圈带有一对支撑架(见图3中的位置B1和B3)。该高速轴专门设计用于高达35 000 r/min的速度。本文采用的航空高速轴承数据是在12 000 r/min转速下和无负载条件下采集的，采样频率为51 200 Hz，共采集了B1位置的轴承7种不同损伤程度工况进行故障诊断，包含正常工况，450 μm内圈故障，250 μm内圈故障，150 μm内圈故障，450 μm滚动体故障，250 μm 滚动体故障和150 μm滚动体故障，每种工况400个样本。

图2 实验台Fig.2 Test rig

图3 航空发动机滚动轴承和主轴Fig.3 Rolling bearings and spindle of an aero-engine

3.2 不同损伤程度的滚动轴承故障诊断结果分析

为验证AACNN对航空高速轴承故障诊断的效果，将其与注意力机制+深度卷积神经网络(ACNN)进行对比研究。首先，分别对轴承振动信号进行WPD[19]、VMD[20]和EMD[21]，提取特征模量；然后，将特征模量分别通过AACNN与ACNN进行训练，AACNN按上述1.2节中第4步设计，对比的ACNN模型则将注意力增强卷积层直接换为“注意力机制+卷积层”，其他参数不变。通过模型对比验证所提方法的自适应特征提取能力和故障识别能力。

对于WPD-AACNN模型，将采集到的信号样本进行WPD，对其进行3层分解，得到8个低频和高频分量信号特征模量，如图4所示。然后将其堆叠成一个多通道的信号特征样本。按图1中的故障诊断流程，通过AACNN对其进行特征融合和分类识别，识别结果如图5所示，训练集和测试集的损失函数曲线逐渐收敛并稳定下降，测试集准确率约为99%，两条曲线几乎重合，模型过程中也并未产生过拟合。

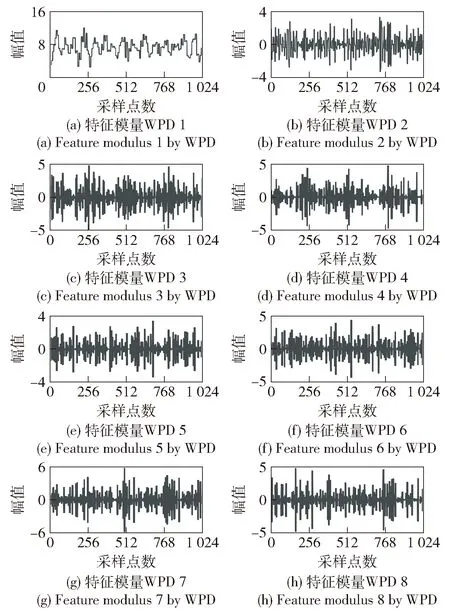
图4 轴承250 μm内圈故障WPD特征模量Fig.4 Feature modulus of the faults of a 250 μm inner ring using WPD

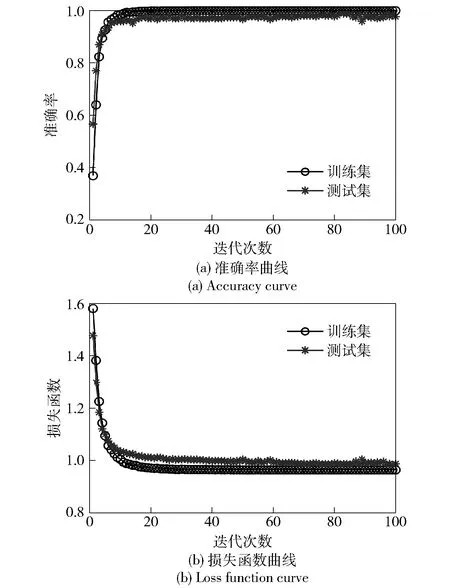
图5 WPD-AACNN 模型诊断曲线图Fig.5 Diagnostic curve of the WPD-AACNN model

为更好地对模型进行分析，挖掘模型提取的隐式特征，采用t-SNE算法对模型中的卷积层的高维输出进行降维，使高维数据可视化。由于散点图的坐标轴无实际意义，采用P1、P2来表示[22]。图6为输入数据经WPD-AACNN模型训练后注意力增强卷积层和其余卷积层的输出特征可视化散点图。观察图6可以发现，经过卷积层提取特征后，不同故障特征逐渐聚拢，到了第4层各状态特征之间已经明显分开。

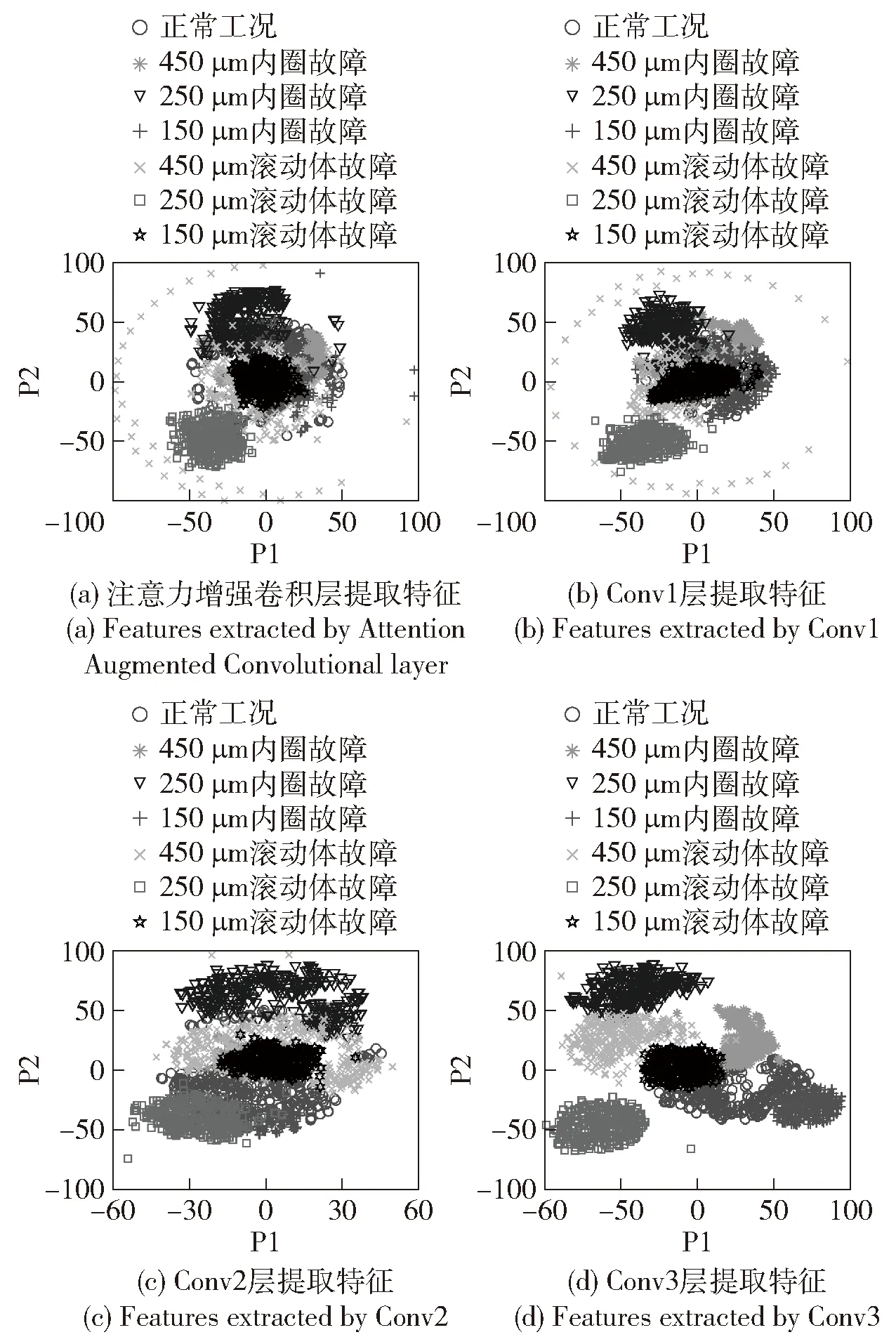
图6 WPD-AACNN模型卷积层t-SNE特征散点图Fig.6 Scatter plot of features extracted by convolution layers of the WPD-AACNN model using t-SNE

同样，采用相同的多通道特征模量样本，训练WPD-ACNN模型，所得结果如图7所示，准确率为95%左右，损失函数曲线平稳收敛，模型收敛较好。图8是输入数据经WPD-ACNN模型训练后各卷积层的特征可视化散点图。可以发现每层的不同故障特征逐渐聚拢，到了第4层各状态特征之间已经明显分开。但与图6相比，由于AACNN关注了全局信息，可以将不同工况下故障特征聚合得更好、更精确。

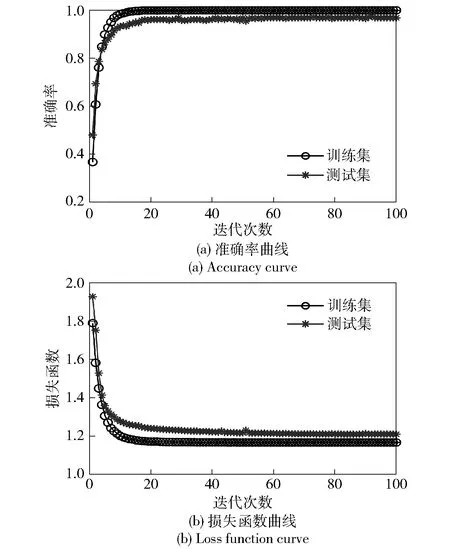
图7 WPD-ACNN模型诊断曲线图Fig.7 Diagnostic curve of the WPD-ACNN model

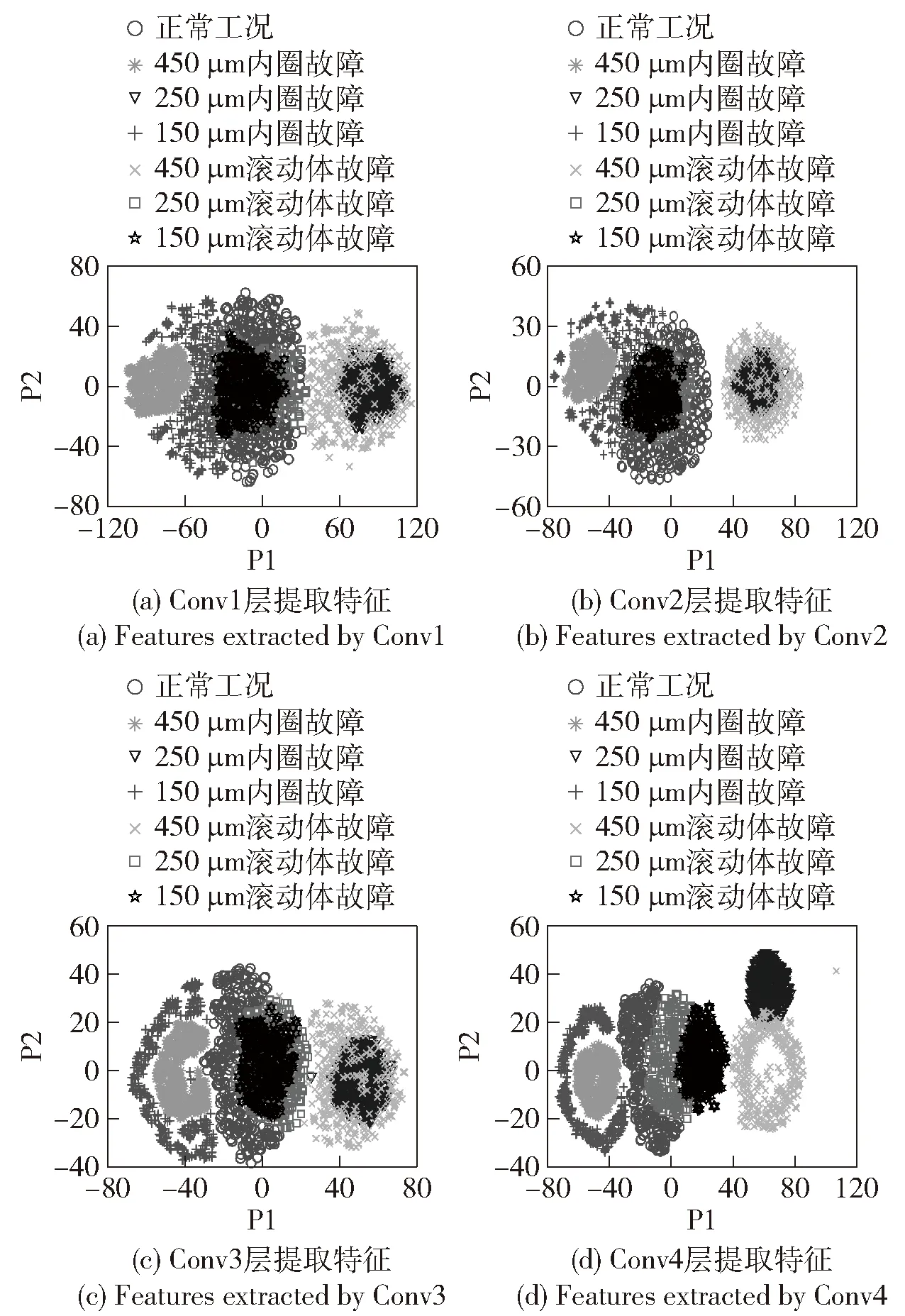
图8 WPD-ACNN模型卷积层t-SNE特征散点图Fig.8 Scatter plot of features extracted by convolution layers of WPD-ACNN model using t-SNE

对于VMD-AACNN模型，通过VMD对信号进行分解。将原始信号进行分解为如图9所示的3层，并作为特征模量构造多通道样本输入，进行AACNN模型训练。所得结果如图10所示。准确率为95%左右，训练集和测试集两条曲线几乎重合，训练集和测试集损失函数 曲线逐渐收敛并稳定下降，模型过程中也并未产生过拟合。图11是输入经过VMD-AACNN模型训练后注意力增强卷积层和其余卷积层的输出特征可视化散点图。可以发现不同故障特征逐渐聚拢，到了第4层各状态特征之间几乎明显分开，只有部分特征重叠，不同类故障未完全分开。

图9 轴承250 μm内圈故障VMD特征模量Fig.9 Feature moduli of the faults of a 250 μm inner ring by VMD

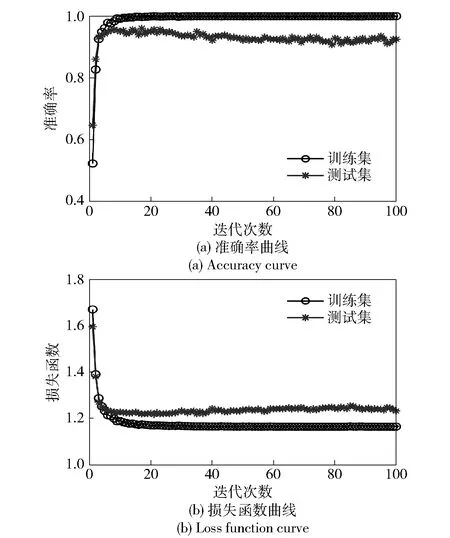
图10 VWD-AACNN损失函数曲线和准确率曲线Fig.10 Diagnostic curve of the VMD-AACNN model

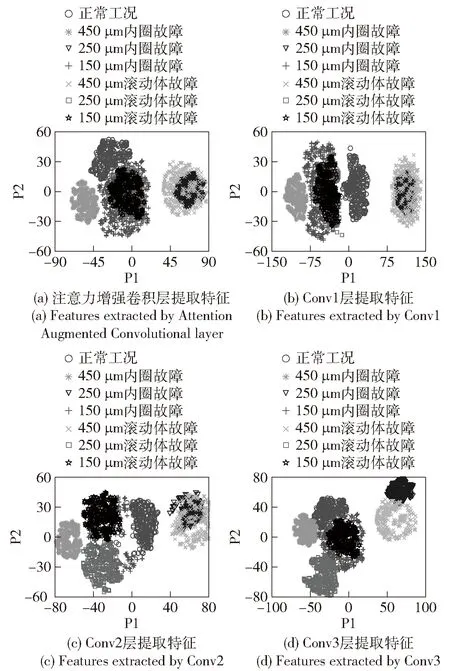
图11 VWD-AACNN卷积层t-SNE特征散点图Fig.11 Scatter plot of features extracted by convolution layers of the VMD-AACNN model using t-SNE

同样，采用相同的VMD多通道特征模量样本，训练VMD-ACNN模型，所得结果如图12所示，准确率为87%左右，损失函数曲线平稳收敛，模型收敛较好。图13为输入经VMD-ACNN模型后各卷积层的特征可视化散点图，可以发现每层的不同故障特征逐渐聚拢，但是到了第4层，部分状态特征之间已经明显分开，还有一些工况特征重叠，没有完全分开。

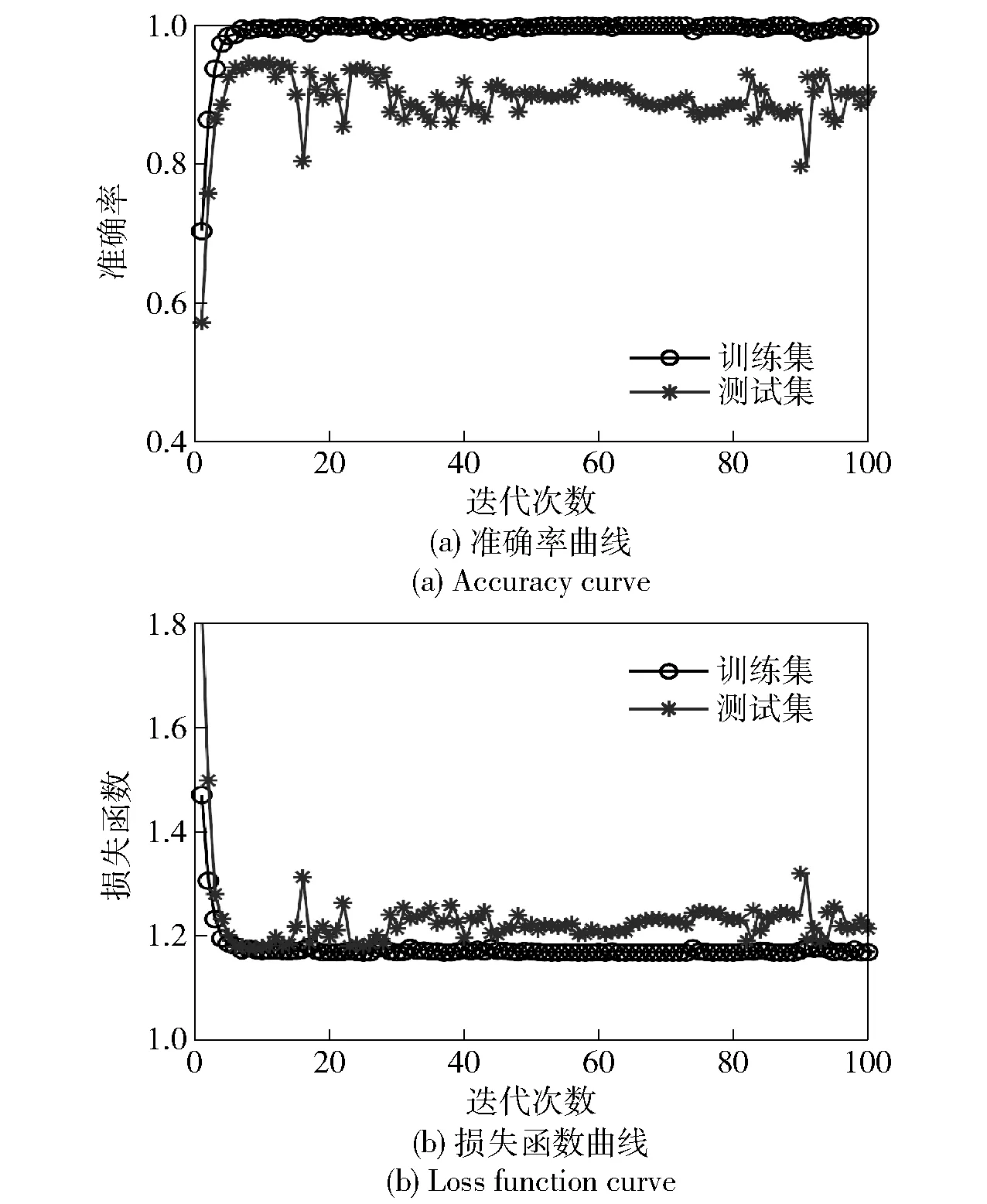
图12 VWD-ACNN模型损失函数曲线和准确率曲线Fig.12 Diagnostic curve of the VMD-ACNN model

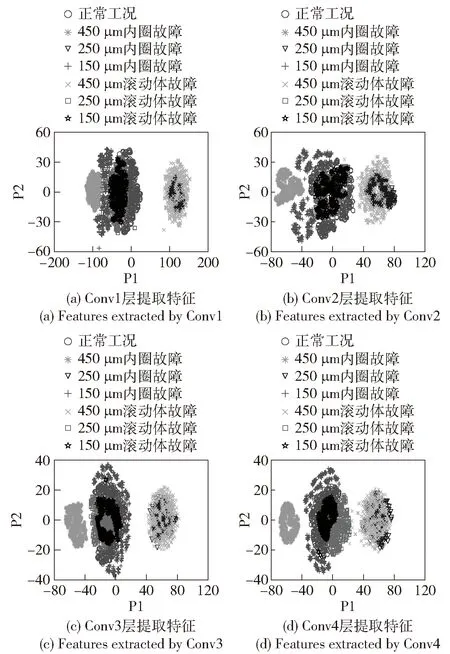
图13 VWD-ACNN模型卷积层t-SNE特征散点图Fig.13 Scatter plot of features extracted by convolution layers of the VMD-ACNN model using t-SNE

对于EMD-AACNN模型，在提取特征模量时，由于EMD对信号样本分解不确定性，通过峭度指标对内禀模式函数(IMF)分量进行选择有效的IMF。轴承250 μm内圈故障通过EMD分解的IMF分量峭度值如图14所示，为了清楚展示取了6个样本。其中一个样本只被分解了5次，与其他样本分解值相差较大，剔除该样本，得到图15所示的IMF分量。对于样本的峭度值从大到小的顺序排列，即IMF3、IMF5、IMF6、IMF2、IMF4和IMF1，按此顺序将6个IMF分量进行堆叠成一个多通道的不同特征样本。

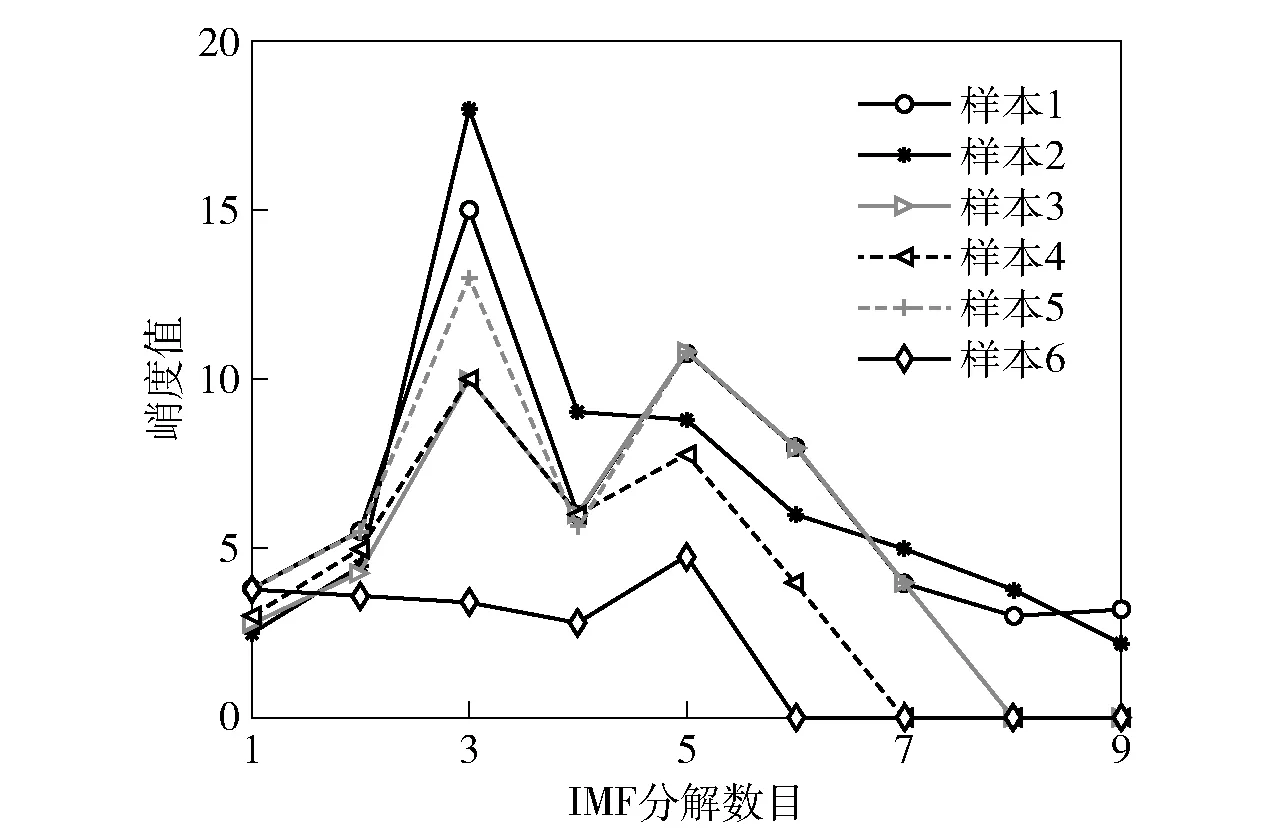
图14 轴承250 μm内圈故障EMD分解IMFs分量峭度值Fig.14 Kurtosis value of IMFs decomposed by EMD for the fault of a 250 μm inner ring bearing

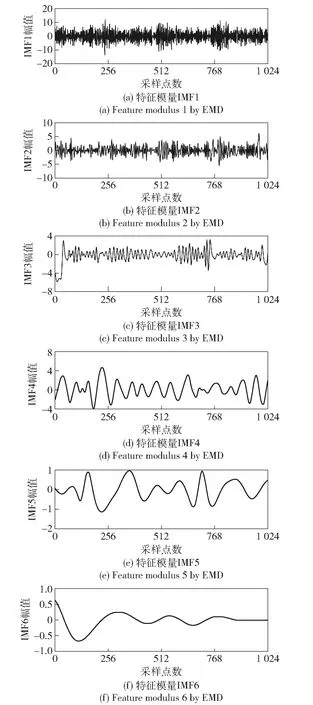
图15 轴承250 μm内圈故障EMD信号分解特征模量Fig.15 Feature moduli of faults of a 250 μm inner ring by EMD

将上述构建好的多通道特征模量样本输入到AACNN模型中进行训练，所得结果如图16所示。训练集和测试集的损失函数曲线逐渐收敛并稳定下降，测试集准确率约为85%，两条曲线几乎重合，模型过程中也并未产生过拟合。图17为输入经EMD-AACNN模型训练后注意力增强卷积层和其余卷积层特征的可视化散点图。可以发现每层的不同故障特征逐渐聚拢，但是各工况特征之间并没有明显分开。

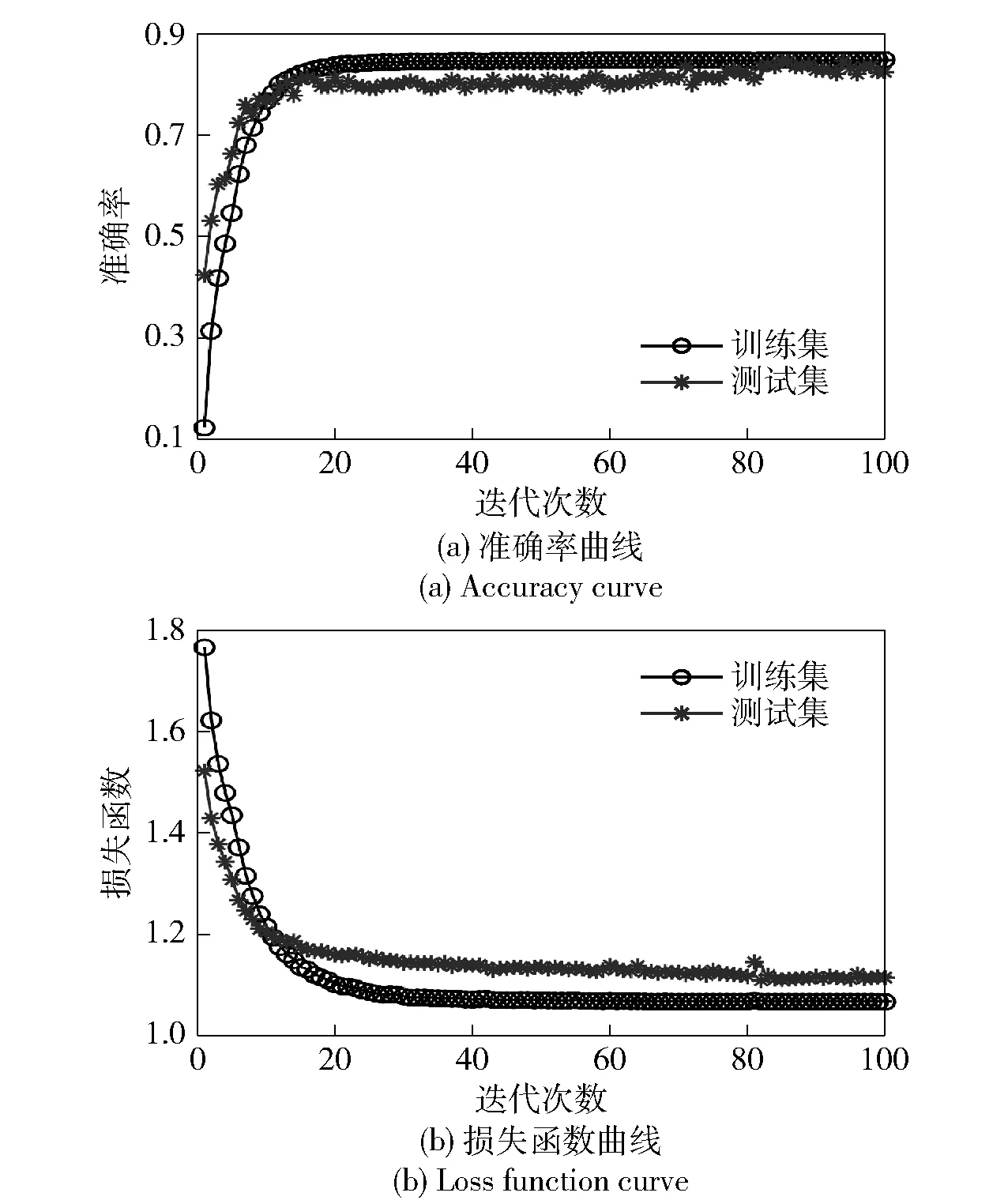
图16 EMD-AACNN模型损失函数曲线和准确率曲线Fig.16 Diagnostic curve of the EMD-AACNN model

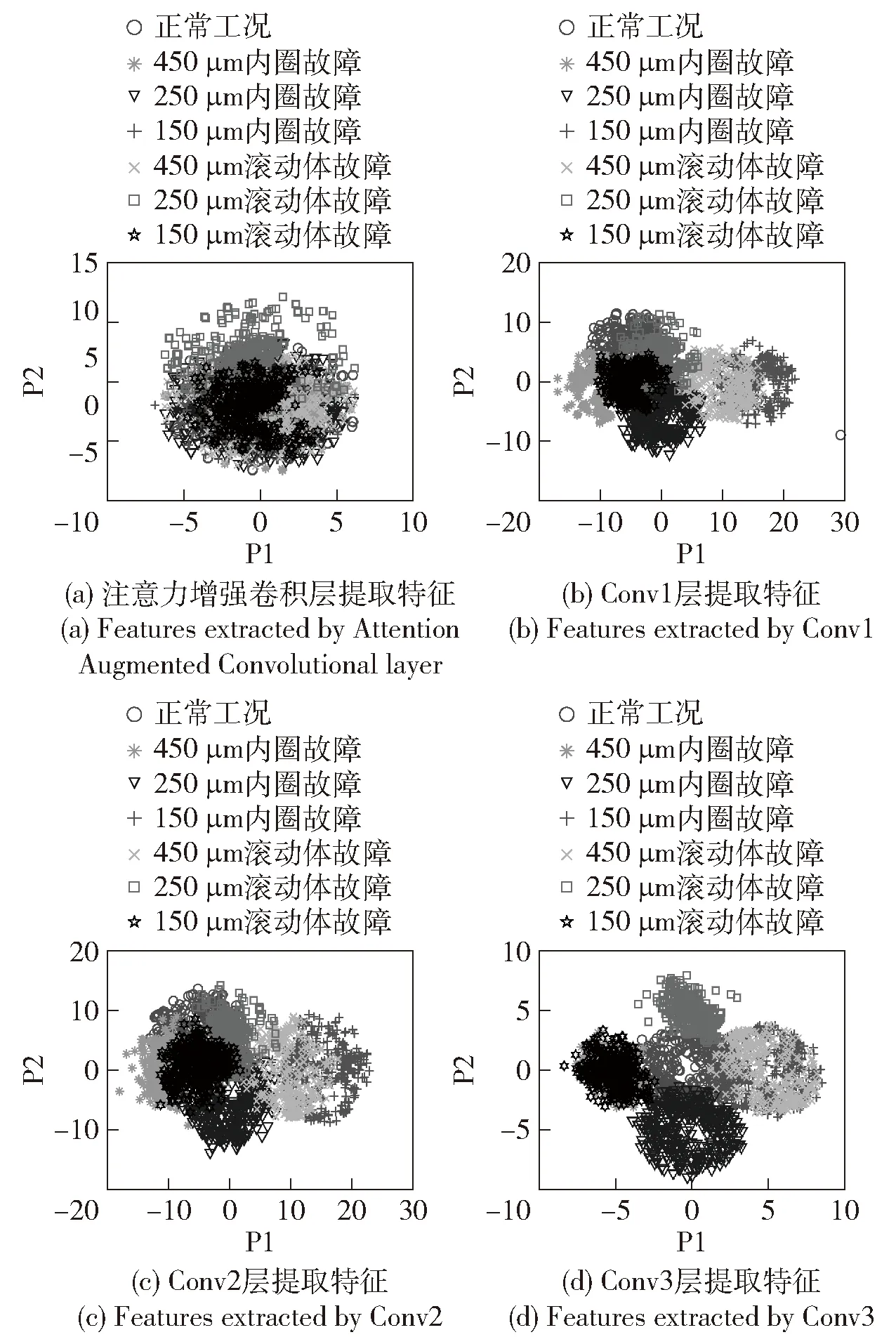
图17 EMD-AACNN卷积层t-SNE特征散点图Fig.17 Scatter plot of features extracted by convolution layers of the EMD-AACNN model using t-SNE

同样，采用EMD多通道特征模量样本，训练EMD-ACNN模型，所得结果如图18所示。准确率约为76%左右，损失函数曲线平稳收敛。图19为输入经EMD-ACNN模型训练后各卷积层的特征可视化散点图。可以发现每层的不同故障特征聚类效果不好，各状态特征之间特征混杂，从而反映了EMD-ACNN模型识别效果不好。

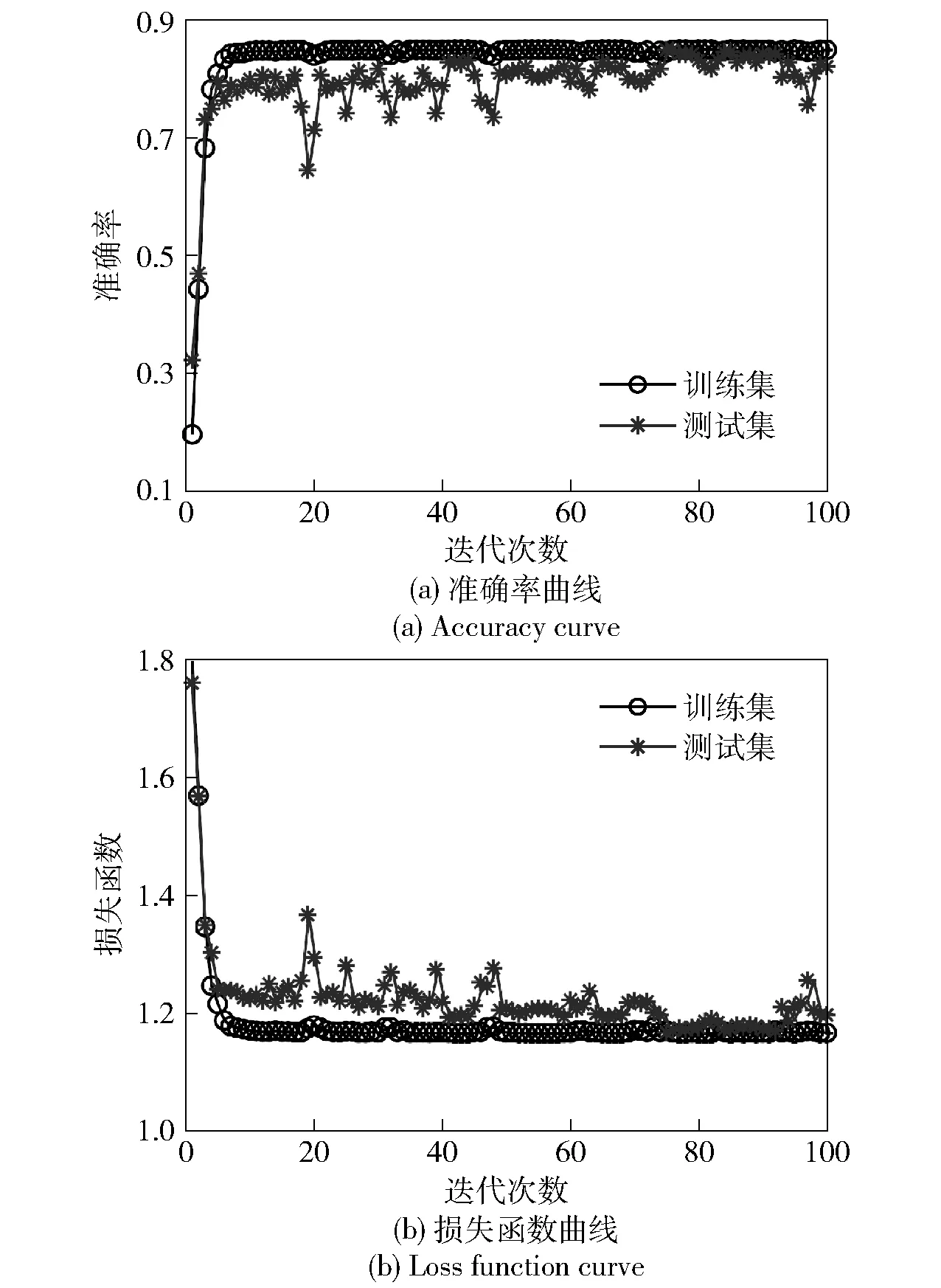
图18 EMD-ACNN模型损失函数曲线和准确率曲线Fig.18 Diagnostic curve of the EMD-ACNN model

图19 EMD-ACNN模型卷积层t-SNE特征散点图Fig.19 Scatter plot of features extracted by convolution layers of the EMD-ACNN model using t-SNE

对上述所建模型通过10-Fold交叉验证来验证模型的性能，所得结果如图20所示。WPD-AACNN的平均准确率为99.02±0.37，VMD-AACNN的平均准确率为95.22±0.83，EMD-AACNN的平均准确率为85.02±1.01，WPD-ACNN的平均准确率为94.85±0.61，VMD-ACNN的平均准确率为87.25±1.21，以及EMD-ACNN的平均准确率为76.11±1.40。

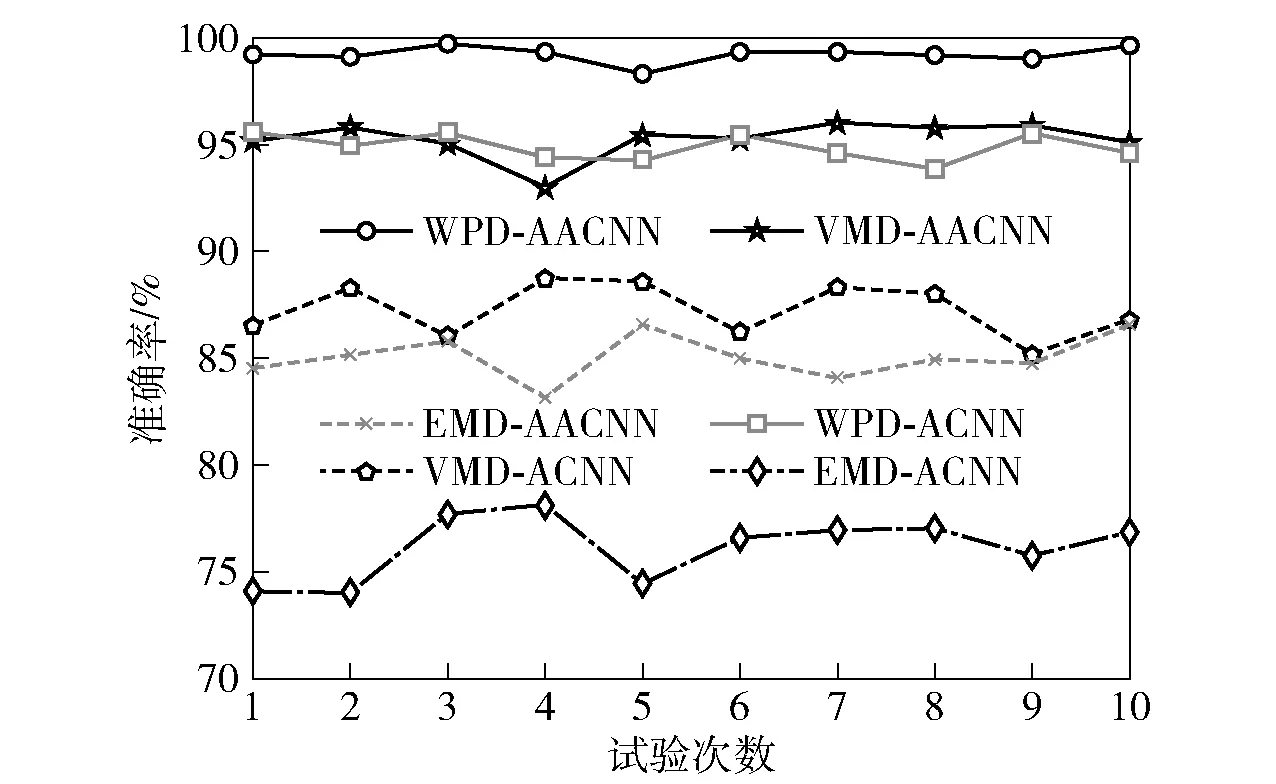
图20 10-Fold交叉验证诊断结果Fig.20 Diagnosis result of 10-fold cross validation

综上所述， AACNN可以有效地对高转速下的滚动轴承进行诊断，可以有效地融合通过信号处理提取的特征模量，而且相比于ACNN，其在融合特征信息时，收敛速度更快。因此，所提算法可以有效地诊断不同损伤程度的滚动轴承故障。

3.3 不同信噪比下模型泛化能力验证

在实际应用中，航空发动机滚动轴承处于噪声的干扰，判断模型是否适应噪声的分析尤为重要。上述实验中，数据为不添加噪声的原始数据，为更好地验证模型在噪声环境下的泛化能力，将上述实验数据添加不同信噪比的高斯白噪声以模拟噪声信号。信噪比SNR定义为信号功率与噪声功率的比值，通常用分贝表示，定义如下：

SNR=10lg(Psignal/Pnoise)

式中：Psignal表示信号的功率值；Pnoise表示噪声的功率值。将SNR设置为-6～4 dB，为信号添加噪声，信噪比越小，噪声功率越大。通过对含噪数据进行训练，不同信噪比下的测试集识别准确率如表2所示。由表2分析可知，在添加噪声后，信噪比越低，原信号的能量比越小，通过WPD、VMD和EMD构建的多通道特征模量样本也会包含更多的噪声信息，通过WPD提取的特征模量包含各频率的故障信息，在输入网络时更容易选择有用的故障特征模量进行特征提取。AACNN相对于“注意力机制+深度卷积神经网络”而言，注意力机制参数也参与了训练，在提取故障信息时选择和关注的信息更精准。虽然AACNN和ACNN都随着信噪比的提升测试集准确率提升，但AACNN模型在低信噪比下依旧能获得较高的准确率，而且在信噪比-2～4 dB中模型较为稳定，能保持较高的准确率。因此，所提模型在强噪声下的环境下，对于滚动轴承可以有效地进行故障诊断。

表2 不同信噪比模型测试准确率Table 2 Test accuracy of different SNR models

4 结论

1)本文提出一种AACNN的滚动轴承故障诊断方法，沿整个网络架构使用了注意力机制，关注全局信息，弥补了深度卷积神经网络卷积层局部感受野特征提取的不足。

2)本文方法可以更好地对信号处理方式提取的特征模量进行融合，进行自适应选择和融合特征模量，更好地关注了全局空间和特征子空间。

3)将本文方法应用于高转速下的航空发动机滚动轴承故障诊断中，对于不同损伤程度的故障可以有效地识别。

4)在不同信噪比的条件下，对本文方法进行训练测试。测试结果表明，本文模型的抗噪性能得到明显提升，并保持一定的诊断精度。