多传感器多目标被动跟踪的“鬼点”形成条件
李松洲, 周荻, 杜润乐, 刘佳琪, 方艺忠
(1.哈尔滨工业大学 航天学院, 哈尔滨 150001; 2.试验物理与计算数学国家级重点实验室, 北京 100076)
0 引言
相比于主动探测跟踪,被动探测跟踪凭借其良好的隐蔽性和生存能力,在军事领域有着更为广阔的应用前景。近些年,关于被动跟踪理论和应用,涌现出大量的研究,如文献[1]对比分析了基于概率假设跟踪方法的扩展卡尔曼滤波和无迹卡尔曼滤波在不同测量噪声水平下求解多传感器多目标被动跟踪问题时性能的优劣;文献[2-5]研究了求解多传感器多目标跟踪的数据关联问题的高效多维分配算法;文献[6-7]研究了异步多传感器多目标跟踪算法;文献[8]比较了两类考虑线程关联的多传感器多目标被动跟踪算法——经典贝叶斯线程关联和蒙特卡洛线程关联对跟踪性能的影响;文献[9-10]研究了基于概率假设密度滤波方法的非关联多目标被动跟踪方法。
被动跟踪问题指的是根据被动传感器获取的目标角度信息估计目标的运动状态,其本质是运用几何上的交叉定位原理,即通过多条测量视线于交汇于目标点处实现对目标的定位。文献[11]指出,该方法能够胜任对单目标的定位跟踪任务,但是在进行多目标的被动定位跟踪时,由于同信道干涉导致“鬼点”问题的出现,使得基于被动测量的跟踪算法在解决多目标跟踪问题时遇到困难。
“鬼点”问题只有在多目标被动跟踪场景下出现,它的本质是来源于不同传感器的多组测量集间的关联不确定性所导致的,当跟踪系统对测量集间进行了不正确关联,将会使系统跟踪到虚假目标点,也就是“鬼点”。一般地,传感器数目越多,获取的测量信息越多,能够有效降低这种关联不确定性。因此,文献[11]给出一定条件下完全消除“鬼点”的所需传感器数目必须比目标数多1个的结论,但是没有对传感器数目小于或等于目标数情况下的“鬼点”形成条件进行研究分析。此外,关于被动多传感器多目标跟踪如何有效去除“鬼点”改善跟踪准确率,文献[12-13]的研究都表明在跟踪算法设计中纳入测量频率信息可提高数据关联结果的可靠性达到去“鬼点”的效果,文献[14]指出在进行目标跟踪时进行航迹管理能够抑制“鬼点”生成,文献[15]通过考察两个被动传感器不同信号抵达延时的相关性去除“鬼点”,文献[16]分别论述了通过增加传感器数目、提高测量维度、利用目标状态的先验认知以及其他属性特征等“鬼点”抑制方法,而文献[17]提出了一种采用抵达角度(AoA)和抵达时间(ToA)的被动多传感器多目标跟踪的新型数据关联算法,通过对测量值进行聚类并打分的方式处理面临的“鬼点”问题,这些都属于通过能够有效区分目标和“鬼点”附加信息的获取已达到去除“鬼点”的目的,但是在实际中,很多情况下这类信息要么不存在、要么获取困难。文献[18]利用Hough变换积累单元数和单元投票数进行“鬼点”的判别,达到了消除大部分“鬼点”的目的。文献[19]将模糊集思想进入Hough变换,利用模糊函数的隶属度作为参数空间累积量,在局部和全局两个层次进行联合判决,通过模糊推理最终区分真假航迹。文献[20] 提出一种在干扰环境下新的有效“鬼点”去除算法,证明“鬼点”一般相对于目标具有更高复杂度的轨迹,通过将目标和“鬼点”的轨迹分别近似表征为线性时不变系统的脉冲响应,实现轨迹复杂度和系统阶数的对应,而系统阶数与响应相关的Hankel矩阵秩相等,从而可通过计算比较不同潜在轨迹所对应的Hankel矩阵秩对“鬼点”和目标进行判别。上述几类方法本质上都是利用“鬼点”与目标在几何复杂度上的差异设计的剔除算法,对低几何复杂度的“鬼点”能够起到较好的剔除效果,但是对与目标有着同样几何复杂度的顽固“鬼点”往往却无能为力。文献[21]研究了两个测量平台的仅角度可测的多目标被动跟踪问题,提出一类能够同时有效降低数据关联不确定性和跟踪误差的轨迹优化方法,通过机动改变传感器的位置增加不同方位对目标的观测信息,以达到降低关联不确定性而去“鬼点”的目的,本质上与增加传感器数目的原理类似,而且一般对观测平台的机动能力有较高要求。文献[22]提出一种基于对极几何关联距离的关联代价函数,对传感器原始探测信息间的关联关系进行求解,而后由此进行目标状态估计,避免先估计后关联方式进行大量三角学操作造成误差累计的问题,提高了关联精度,能一定程度上抑制“鬼点”问题,但是这种方法主要适用于基于图像的被动观测问题,具有一定的局限性。此外,文献[22]中所论述的对“鬼点”效应的“免疫”作用并非完全来源于算法优越性,本质上还是增加了传感器数目的作用。上述研究工作主要侧重于对“鬼点”去除算法的研究,对“鬼点”的形成条件没有给出严谨的理论分析结果。本文将着重针对该问题展开研究。
“鬼点”问题是多目标跟踪不可避免的问题,而“鬼点”出现的概率主要与传感器网络和目标群的相对几何关系有关,此外,测量装置的精度以及探测环境的“纯净度”也是影响“鬼点”出现概率的重要因素。“鬼点”不可避免,但是可以消除或者降低其生成概率,这需要根据多传感器多目标被动跟踪问题在不同应用场景下的特点,分析造成“鬼点”出现的主要因素,据此采用不同的“去鬼点”算法,以达到提高跟踪系统准确度和精度的目的,以及节约跟踪系统的组网成本。因此,本文着重研究了多传感器多目标被动跟踪问题中“鬼点”的形成条件,运用集合的分析方法,从理论上分别探究在二维和三维场景下“鬼点”形成的条件,分别分析采用2个、3个和k(k≥2)个传感器进行多目标被动跟踪“鬼点”形成的几何条件,并且给出相关的理论证明和仿真验证实验。
1 “鬼点”问题描述
在二维平面内,只需要两个传感器获取的关于目标的角度信息就可以完成对单个目标进行被动定位跟踪,如图1所示,两传感器s1、s2关于目标点t1的两条射线形成的交会点即为目标位置。
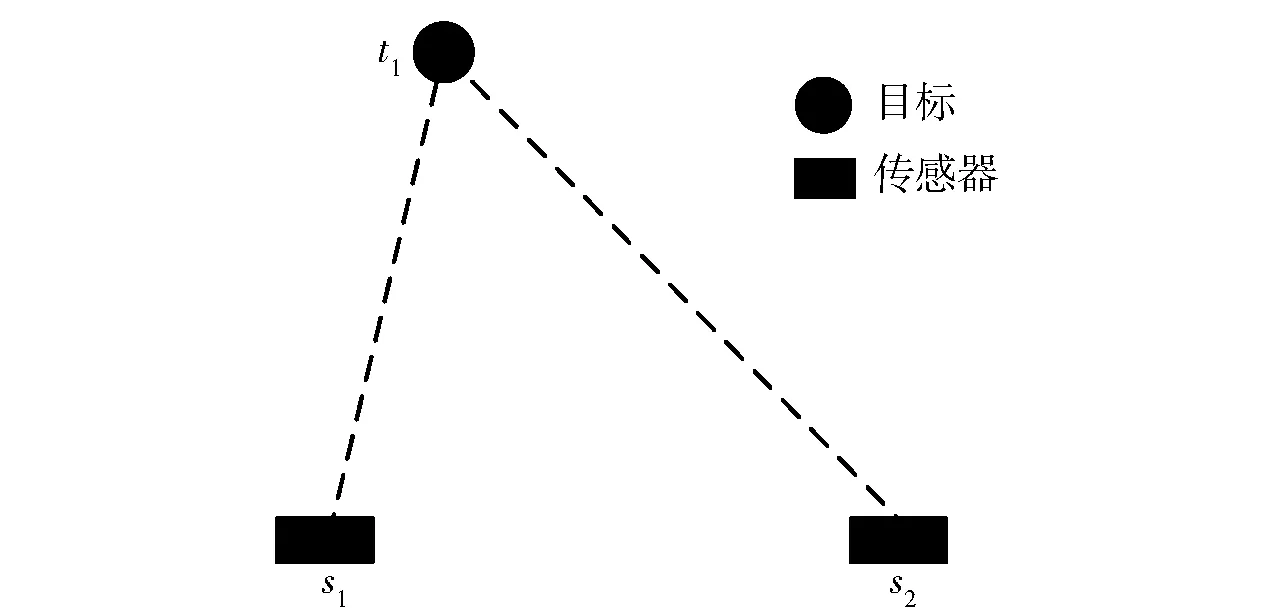
图1 单目标被动定位Fig.1 Passive positioning of a single target
当出现多个目标时(这里以两个目标为例),则可能由于测量信息关联错误,导致不能正确跟踪到目标运动状态,取而代之的将是两个不存在的目标点,一般将这样的虚假目标点称之为“鬼点”,如图2所示,为采用两个传感器s1、s2对两个目标点t1、t2进行被动定位时所构成的相对几何关系,g1和g2为测量信息错误关联时定位到的两个“鬼点”。由图2中可见,跟踪到的“鬼点”位置相对目标真实位置有着明显的偏差,该现象的出现显然不利于工程应用。因此,有必要探究“鬼点”的成因,这将有利于启发多目标被动跟踪设计,减小“鬼点”出现的概率或者避免“鬼点”的形成。
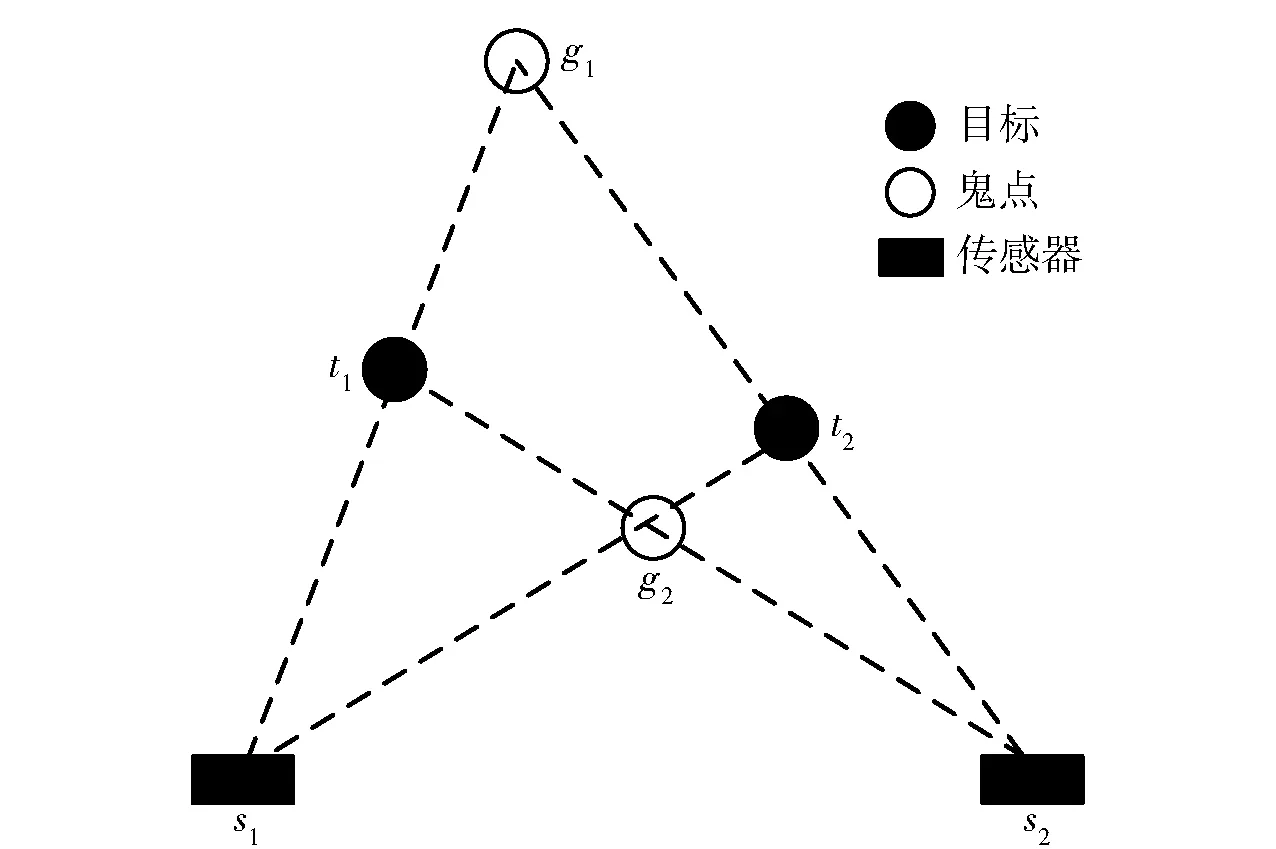
图2 “鬼点”形成示意图Fig.2 Schematic diagram of the formation of ghost nodes
2 “鬼点”形成条件
为了探究多传感器多目标被动跟踪问题中“鬼点”问题的成因,下面将运用集合的分析方法并结合几何原理,对不同场景下的“鬼点”成因进行阐述论证。
设被动传感器位置分别表示为s1,s2,…,sk,目标位置分别表示为t1,t2,…,tp,“鬼点”位置分别表示为g1,g2,…,gq,由传感器si(i=1,2,…,k)获得的视线测量集表示为φi={L(si,t1),L(si,t2),…,L(si,tp)},其中L(si,tj)(i=1,2,…,k,j=1,2,…,p)表示由传感器si指向目标tj的射线。图1中单目标的定位跟踪可表示为
t1=L(s1,t1)∩L(s2,t1)
(1)
图2中的两目标点定位跟踪可表示为
(2)
而当关联错误时出现的“鬼点”则可表示为
(3)
由此,在一般的多目标跟踪定位中,对任意目标的定位可以表示为
tj=L(s1,tj)∩L(s2,tj)∩…∩L(sk,tj)
(4)
针对图2中所示的“鬼点”问题,倘若额外增加一号传感器s3,如图3所示,由于此时传感器s3获取的测量视线L(s3,t1)和L(s3,t2)不再通过点g1和g2,即3个传感器获取的测量视线除了在目标点t1和t2交汇外,并没有形成其他不同于这两点的公共交汇点,这时将不会定位到“鬼点”。
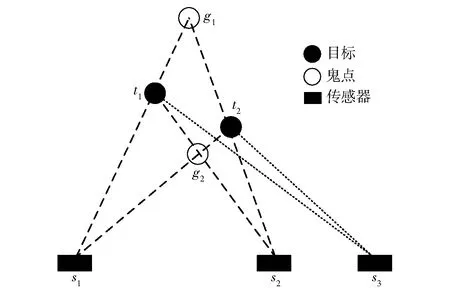
图3 三传感器对两目标的被动定位Fig.3 Passive positioning of two targets using three sensors
关于上述现象,文献[11]给出了如下一般性结论:
引理1假设任意两个传感器不与任一目标共线(假设1),则要实现对传感器公共探测区内的p个目标进行准确(不出现“鬼点”)的被动定位,最多需要p+1个传感器进行被动测量。
关于引理1尽管文献[11]已经给出了相应的证明,但鉴于原证明略显含糊晦涩,这里给出该命题的详细证明过程。
关于引理1的数学证明,可以通过反证法证明,下面给出证明过程。
证明设公共观测区域(不局限于平面)内有p个目标(分别标记为t1,t2,…,tp),现在采用k个传感器(分别标记为s1,s2,…,sk)对这p个目标进行被动定位,且传感器位置为目标位置满足“任意两个传感器不与任一目标共线”的假设条件。现假如该情境下定位到一“鬼点”gl,则gl应为k个传感器得到的k条观测视线公共交点,即
gl=L(s1,tj1)∩L(s2,tj2)∩…∩L(sk,tjk)
(5)
式中:ji∈{1,2,…,p}(i=1,2,…,k)为定位到“鬼点”gl时传感器si指向“鬼点”gl射线上的目标点标号。根据“鬼点”的物理意义,gl还须满足
∀i∈{1,2,…,k},gl≠tji
(6)
下面首先证明:在(5)式中,∀jm,jn,m≠n,恒有jm≠jn(命题1)。
根据“鬼点”的定义,“鬼点”必然处在传感器与目标形成的视线之上。现在假设∃jm,jn,m≠n,有jm=jn(假设2),从而有
tjm=tjn∈{L(sm,tjm)∩L(sn,tjn)}
(7)
则由(5)式可知
gl∈{L(sm,tjm)∩L(sn,tjn)}
(8)
由(7)式和(8)式可知,直线L(sm,tjm)和L(sn,tjn)存在交点tjm和gl,而由(6)式可知gl≠tjm,所以直线(射线)L(sm,tjm)和L(sn,tjn)重合,这样sm、sn与tjm共线,不满足假设1,所以假设2不成立,命题1得证,即(5)式中的tj1,tj2,…,tjk须为t1,t2,…,tp中任意k个点的一个排列。
所以,k≤p是得到“鬼点”的必要条件,由与该命题等价的逆否命题“当k>p时将不可能形成‘鬼点’”可知引理1成立,引理1得证。
在上述证明过程中并没有对观测区域作出限制条件,所以引理1的结论既适用于二维场景,同样也适用于三维场景。
由引理1可知,当k>p时,即传感器数目大于目标数目时,可以避免“鬼点”的形成。那么,当k≤p时是否一定会形成“鬼点”呢?该条件下“鬼点”形成又是否需要什么特殊的条件?关于该问题的探索鲜见相关的研究成果,但这并不意味着该问题的探究没有意义。倘若能够揭示该条件下“鬼点”成因,那么就能据此在实际应用中通过跟踪方案设计尽可能地给“鬼点”形成创造不利条件从而达到抑制“鬼点”生成概率,改善跟踪系统性能,并且一定程度上降低跟踪系统的组网成本。
2.1 两传感多目标被动跟踪
对于两传感器多目标被动跟踪问题,有如下定理:
定理1对于目标点与传感器共面时,只要当存在两目标点位于两传感器基线同侧时才有可能形成“鬼点”,且当两目标点在基线上的投影距离大于基线长度时定位到“鬼点”的可能性将有所降低;而当任意两目标点与传感器构成异面关系时,则不会定位到“鬼点”。


图4 两传感器被动定位Fig.4 Passive positioning using two sensors
当任意两目标点与传感器构成异面关系时,根据定理1,若假设该场景下定位到“鬼点”gl,则必然存在两个目标,设为tj1和tj2,满足条件:
gl=L(s1,tj1)∩L(s2,tj2) orgl=L(s1,tj2)∩L(s2,tj1)
(9)
由场景设置条件“任意两目标点与传感器构成异面关系”知,L(s1,tj1)与L(s2,tj2)异面无交点,L(s1,tj2)与L(s2,tj1)同样如此,因此假设不成立,定理得证。
根据前文所述,当gl满足(5)式时其必然满足(9)式,即(9)式是(5)式的必然条件。所以可以得到如下推论:
推论1在多传感器多目标被动跟踪场景下,当存在两个传感器使得任意两个目标都与这两个传感器构成异面关系时,将不会定位到“鬼点”。
根据上述分析讨论,得到如下结论:当采用两个传感器进行被动跟踪时,唯有目标群满足如下两个条件时才可能定位跟踪到“鬼点”:
1) 目标群中至少存在两个目标点与两传感器共面;
2) 与传感器共面目标点位于传感器观测基线同侧。
2.2 三传感多目标被动跟踪
当采用3个传感器进行被动跟踪时,根据引理1,只有当目标群中目标数p≥3时才有可能跟踪到“鬼点”。下面在p≥3的条件下,分析“鬼点”形成问题:
1) 3个传感器s1、s2、s3共线时,有如下定理:
定理2当采用3个共线传感器s1、s2、s3进行多目标被动跟踪时,当至少存在3个目标tj1、tj2、tj3与s1、s2、s3构成共面关系才有可能跟踪到“鬼点”。
证明:假设有“鬼点”gl满足
gl=L(s1,tj1)∩L(s2,tj2)∩L(s3,tj3)
(10)
若令S=al(s1,tj1)+bl(s2,tj2)(a、b为任意实数)表示由射线L(s1,tj1)的方向向量l(s1,tj1)和射线L(s2,tj2)的方向向量l(s2,tj2)张成的平面,则由“s1、s2、s3共线”知s3∈S,由(10)式知gl∈L(s3,tj3)且gl∈S,而gl≠s3,所以有L(s3,tj3)⊂S,从而tj3∈S,得证。
由此进一步得到推论:
推论2k个共线传感器被动观测p≥k个目标的情况,可以得到至少存在k个目标tj1,tj2,…,tjk与s1,s2,…,sk构成共面关系才有可能跟踪到“鬼点”。
证明假设有鬼点gl满足
gl=L(s1,tj1)∩L(s2,tj2)∩…∩L(sk,tjk)
(11)
若令S=al(s1,tj1)+bl(s2,tj2)(a、b为任意实数)表示由射线L(s1,tj1)的方向向量l(s1,tj1)和射线L(s2,tj2)的方向向量l(s2,tj2)张成的平面,则由“s1,s2,…,sk共线”知,对任意的传感器si(i=1,2,…,k)都有si∈S,由(11)式知gl∈L(si,tji)且gl∈S,而gl≠si,所以有L(si,tji)⊂S,从而tji∈S。根据i的任意性可知,目标群中至少存在k个目标tj1,tj2,…,tjk与s1,s2,…,sk构成共面关系,得证。
2) 3个传感器s1、s2、s3不共线,有如下结论:

证明假设有“鬼点”gl满足
gl=L(s1,tj1)∩L(s2,tj2)∩L(s3,tj3)
(12)

根据上述分析结果,可以类推得到:

证明假设有“鬼点”gl满足
gl=L(s1,tj1)∩L(s2,tj2)∩…∩L(sk,tjk)
(13)
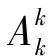
2.3 一般多传感器多目标被动跟踪问题
针对一般多传感器多目标被动跟踪问题,有如下结论:
定理4对于非合作目标(目标的空间分布不可知,具有任意性)的被动跟踪,当k≤p(k≥2)时,“鬼点”存在的可能性恒正。
证明:设有k个传感器在空间任意分布,如图5中所示的s1,s2,…,sk,在空间另外任找一点gl,当空间中存在k个目标点位置t1,t2,…,tk分别落在射线L(s1,gl),L(s2,gl),…,L(sk,gl)上时,则能使gl满足(5)式所述“鬼点”形成条件,跟踪到“鬼点”gl,而由目标分布的“任意性”可知,总可以找到这样的k个目标点位置t1,t2,…,tk。所以,当k≤p时,“鬼点”存在的可能性恒为正,定理得证。

图5 k个传感器被动跟踪p个目标 “鬼点”形成示意图Fig.5 Formation of ghost nodes in passive tracking for p targets using k sensors
这里需要指出的是,上述结论均是基于理想测量假设,即不考虑测量误差的影响。但是,这些结论对于实际应用同样存在着重要的启发意义,应用中由于测量误差随机性的存在,当实际几何关系“十分接近”结论中所述条件时,便可判定满足“鬼点”形成条件。这样,合理地设计这种“接近程度”的度量机制则至关重要,这也将是下一步研究工作。
3 仿真实验及分析
第2节所述的多条定理,均已给出明晰的证明过程,为进一步对上述结论进行论证,现设置三组跟踪仿真实验,对上述结论进行仿真验证。
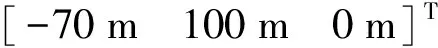
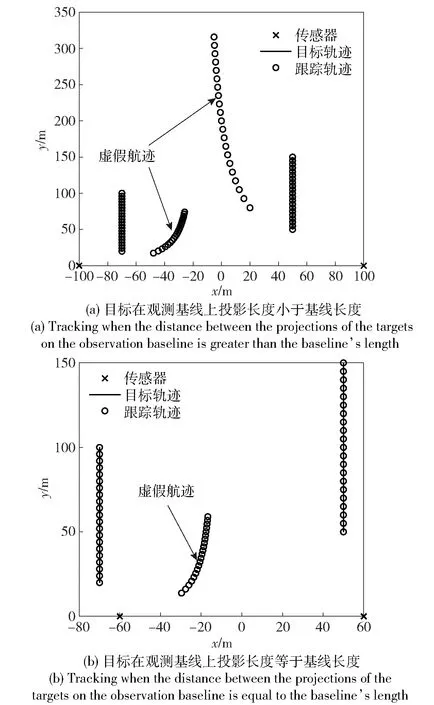
图6 两传感器与两目标共面条件下的跟踪结果Fig.6 Tracking results of two targets using two sensors coplanar with targets
若不改变s1、s2的位置,仅仅在[0 m 0 m 0 m]T额外设置第3号传感器s3,则得到如图7所示的仿真结果,可见传感器网络没有跟踪到虚假航迹,验证了引理1所述结论,说明增加传感器数目能够抑制乃至消除“鬼点”。

图7 增加第3号传感器共面条件下的跟踪结果Fig.7 Tracking result of two targets using three sensors coplanar with targets

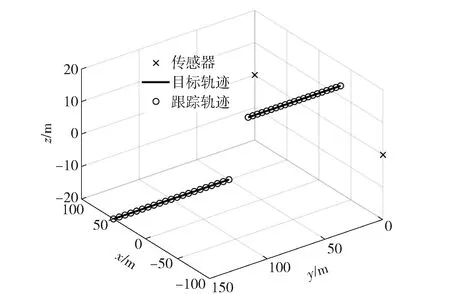
图8 两传感器与目标异面条件下的跟踪结果Fig.8 Tracking result of two targets using two sensors non-coplanar with targets
实验2设有3个目标t1、t2、t3分别从[-70 m 100 m 0 m]T、[-10 m 200 m 0 m]T、[40 m 200 m 0 m]T处以[0 m/s -1.2 m/s 0 m/s]T、[0 m/s -1.6 m/s 0 m/s]T、[0 m/s -1.6 m/s 0 m/s]T的速度运动,现设置3个传感器s1、s2、s2分别位于[-100 m 0 m 0 m]T、[0 m 0 m 0 m]T、[100 m 0 m 0 m]T处对这3个目标进行被动观测并跟踪,这时3个传感器共线,且与3个目标共面,得到的仿真结果如图9(a)所示,跟踪到了一条由“鬼点”构成的虚假轨迹。而当将目标t2的起始位置设置为[-10 m 200 m 20 m]T使得3个共线传感器这时与3个目标不再共面时,得到如图9(b)所示的跟踪结果,虚假航迹不再出现。该组仿真实验对定理2所述结论起到了验证作用,同样表明了提高传感器网络相对目标团的空间布局复杂度对“鬼点”的抑制作用。
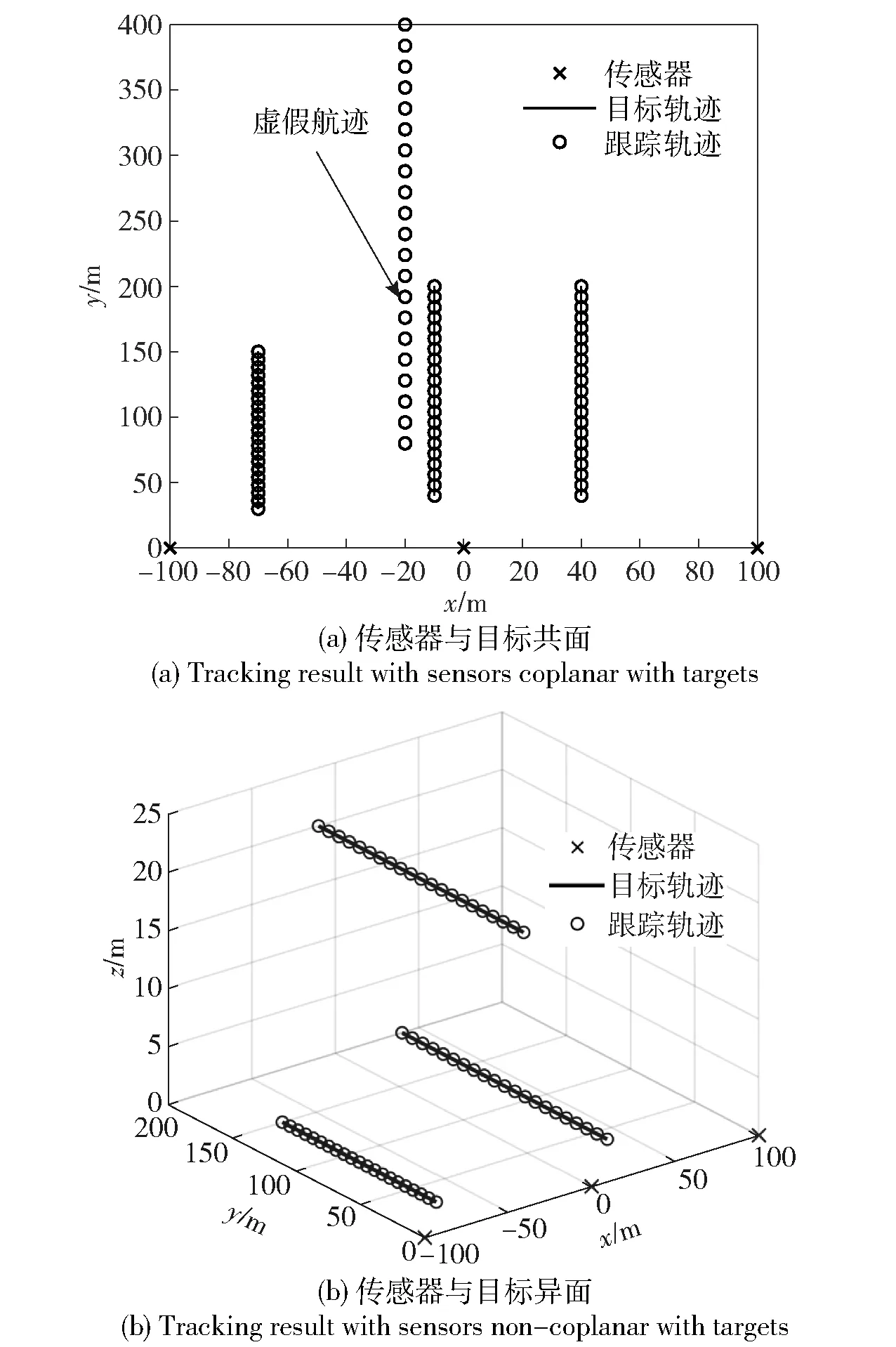
图9 三共线传感器与目标共面/ 异面条件下的跟踪结果Fig.9 Result of tracking three targets using three colinear sensors coplanar/non-coplanar with targets
根据第2节对定理3和定理4的分析证明过程,二者所述结论本质上具有一致性,可归纳统一于上节所述的推论3,推论3包含定理3所述结论,而定理4中“鬼点”存在的前提也包含在推论3所述结论之中。据此设置仿真实验3对该组结论进行仿真验证。
实验3不失一般性,设置3个传感器s1、s2、s2分别位于[-100 m 0 m 0 m]T、[0 m 0 m 50 m]T、[100 m 0 m 0 m]T处对空间中3个非合作目标进行被动观测并跟踪,3个目标的运行轨迹分别为
式中:t为仿真时间,t∈[0 s,100 s]。这时由于3个目标点运动形式的特殊性,使得在整个运动过程中射线L(s1,t1)、L(s2,t2)、L(s3,t3)始终存在着公共交点,导致最终跟踪到一条由“鬼点”构成的虚假轨迹,对应的仿真结果如图10所示,对定理3、定理4以及推论3进行了有效验证。

图10 非共线三传感器对非合作目标的跟踪结果Fig.10 Tracking result of non-cooperative targets using three non-colinear sensors
同样,通过设置6个传感器均匀分布在半径为80 m上的圆上对目标群进行被动观测并跟踪,若目标群中存在6个目标同样以圆形阵列(如图11中6个目标均匀分布在半径为100 m的圆上)朝着传感器方向运动时,传感器与6个目标的某种“一一配对关系”所构成的6条射线始终存在公共交点,使得传感器网络最终跟踪到了如图11所示的7条轨迹,可见其中位于中心位置的一条为由“鬼点”组成的虚假轨迹,该结果进一步验证了推论3及定理4所述结论。
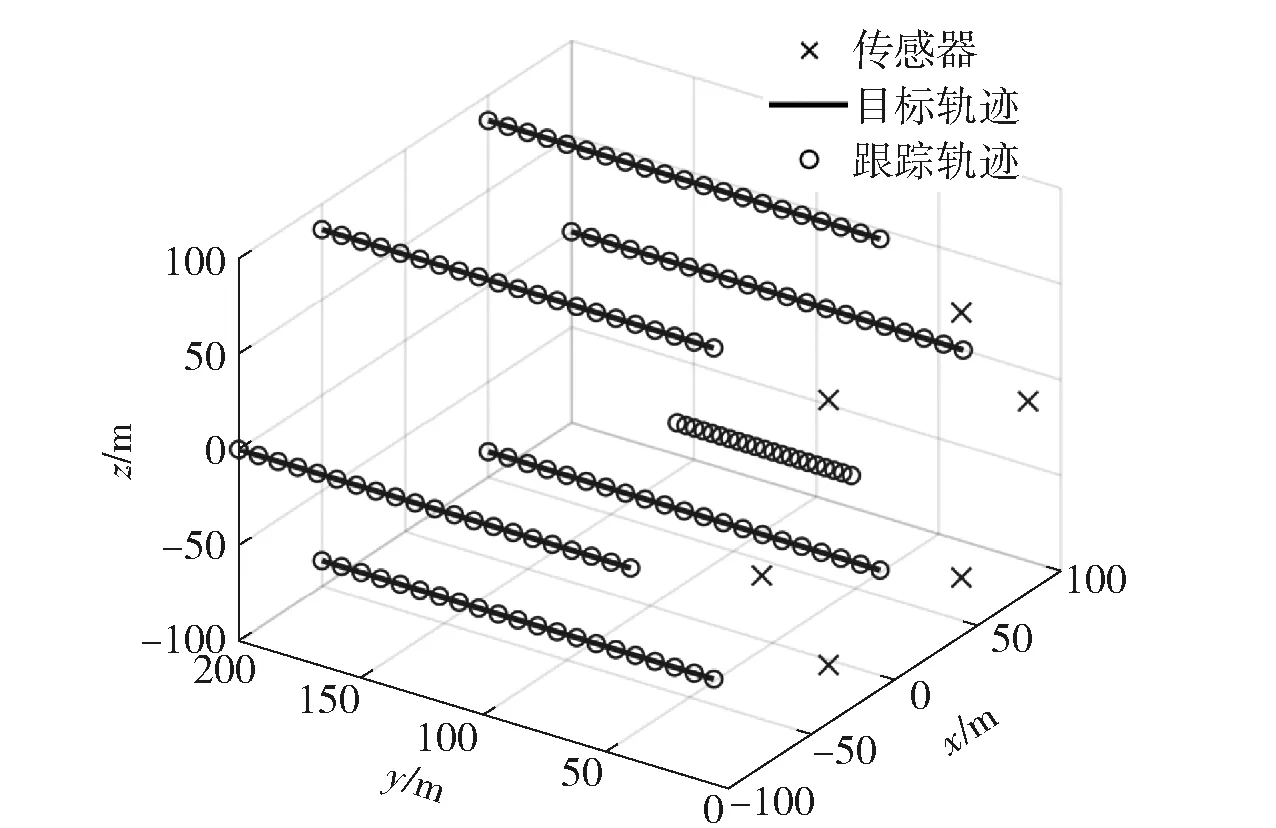
图11 非共线六传感器对非合作目标的跟踪结果Fig.11 Tracking result of non-cooperative targets using six non-colinear sensors
4 结论
针对多目标被动跟踪由于测量数据集的关联不确定性带来的“鬼点”问题,本文运用集合分析方法,从几何角度分别分析了两传感器、三传感器和任意多传感器的跟踪场景下的“鬼点”形成条件。得到如下主要结论:
1) 当采用两传感器被动跟踪时,目标群须满足目标群中至少存在两个目标点与两传感器共面、与传感器共面目标点位于传感器观测基线同侧的几何分布条件才有可能在目标跟踪过程中形成“鬼点”,且当目标点在观测基线上的投影距离小于基线长度时,“鬼点”形成概率降低;

3) 对于非合作目标(目标的空间分布不可知,具有任意性)的被动跟踪,当k≤p时,“鬼点”存在的可能性恒为正。
上述结论主要从几何层面揭示了多目标被动跟踪过程中“鬼点”的形成条件,表明在求解被动跟踪问题时,适当减小传感器观测基线长度、提高传感器网络相对目标团的空间布局复杂度、增加传感器数目均能起到一定的“鬼点”抑制作用。在实际应用中,可根据本文相关结论对跟踪算法进行优化设计,或者对跟踪网络的组建和布局进行特殊设计,尽可能给“鬼点”的形成创造不利条件,从而达到抑制和消除“鬼点”的目的,改善被动跟踪系统的可靠性。因此,本文的研究工作对多目标被动跟踪的工程应用具有一定指导意义。

