基于履带式联合收获机转向特性的局部跟踪路径规划
何永强 周 俊 袁立存 郑彭元 梁子安
(南京农业大学工学院,南京 210031)
0 引言
农业机械自动导航控制是实现无人生产作业的关键技术,优化农机在非结构化环境条件下的跟踪控制方法是近年来的研究热点,对提高作业质量和作业效率具有重要意义[1-4]。
履带式车辆与地面接触面积大,对耕作层土壤破坏小、通过性好,其中履带式联合收获机被广泛应用于水田收获作业,并逐步步入无人化阶段。导航控制中履带式与轮式车辆转向原理不同,轮式车辆的转向控制参数与转向轮偏角数学关系明确,转向控制频率越高,跟踪轨迹越平滑紧凑,越有利于农机通过连续小角度近似线性调整纠偏上线[5-9]。而履带式联合收获机底盘行走系统通常采用变速箱加静液压无级变速器(Hydro static transmission,HST),依靠多片式摩擦离合器单边制动转向,转向半径与摩擦制动程度有关,不易通过理论计算获得转向控制参数与实际转向半径之间的关系[10],适用于履带式车辆转向特性的导航路径跟踪技术难题还未得到有效解决[11]。鉴于此,国内外学者针对履带式联合收获机转向控制参数与实际运动特性之间的关系进行了深入研究。NOGUCHI团队[12-13]通过田间试验建立了行走、转向控制参数与转向角速度之间的关系,利用履带式联合收获机运动状态方程解算到达目标位置所需的转向控制量。关卓怀[14]基于最小二乘支持向量机(LS-SVM)提出在线识别履带式联合收获机转向控制模型,通过动态拟合实际转向率和占空比的函数关系修正转向控制模型,利用周期性圆弧-切线交替循环行进策略实施路径跟踪控制。上述学者通过离线或在线的方式获得了转向控制参数与实际转向运动特性之间的关系,并利用小周期多段圆弧平滑衔接进行路径跟踪,提高了路径跟踪精度。但履带式车辆位姿调整控制过程中,转向半径变化频率较高,易加剧离合器结合冲击[15-16],且会引起液压系统振荡冲击,进而导致液压油路、管件加速损坏,不利于控制系统的稳定[17-19]。作业时收获机沉陷、滑移、液压系统时滞等现象导致高频转向激励信号无法使车辆及时稳定响应预设动作,进而导致控制超调、系统响应滞后等影响跟踪精度的问题[20-22]。因此,传统小周期追踪控制方法在单边制动转向履带式农机的实际生产应用中还存在一定的局限性,研发适用于农机转向特性的低频导航控制方法对提高导航精度和系统稳定性具有重要意义。
针对上述问题,本文提出一种基于履带式联合收获机转向特性的预瞄-切线局部跟踪路径动态规划算法,通过构建履带式联合收获机跟踪控制试验平台进行田间试验研究,验证该跟踪控制算法的有效性,以期为履带式农机导航跟踪控制提供参考。
1 局部跟踪路径规划
1.1 预瞄-切线局部跟踪路径动态规划算法原理
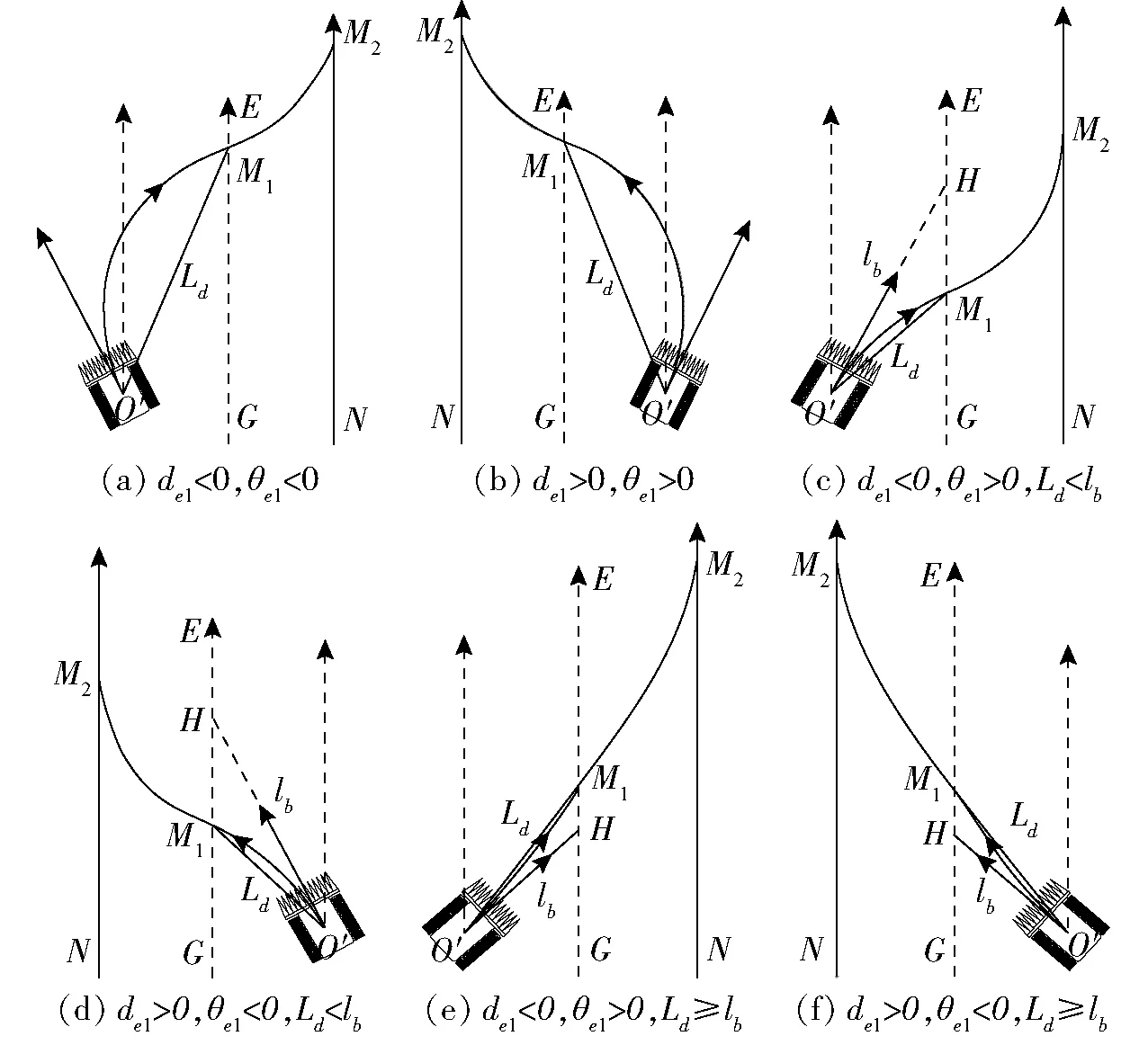
局部跟踪路径是农机按照一定的跟踪策略,规划从当前位置趋近期望路径的行驶路线,合理的局部跟踪路径可极大提高农机的导航精度和稳定性。预瞄-切线法动态规划的跟踪路径由平滑连接的两段弧线组成,第1段圆弧由收获机当前位姿与1/2横向偏差线上的预瞄点确定,第2段圆弧由收获机在1/2横向偏差线的实际位姿与期望路径的相切几何关系确定。如图1所示,在车体坐标系xOy下收获机当前位置为点O,y轴正方向为收获机前进方向,x轴正方向指向车体右侧,期望路径为直线N1M2,线段ON1长度为初始横向偏差de1;射线Oy为收获机当前航向,OE1与N1M2平行,初始航向偏差为θe1;点G为ON1的中点,1/2横向偏差线GE2平行于期望路径N1M2。dmin为允许横向偏差。

图1 预瞄-切线局部跟踪路径规划
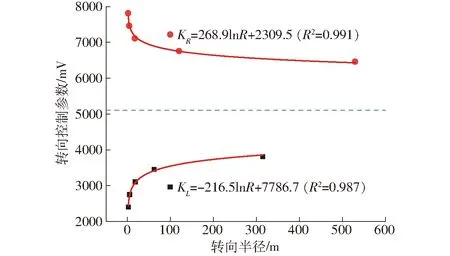
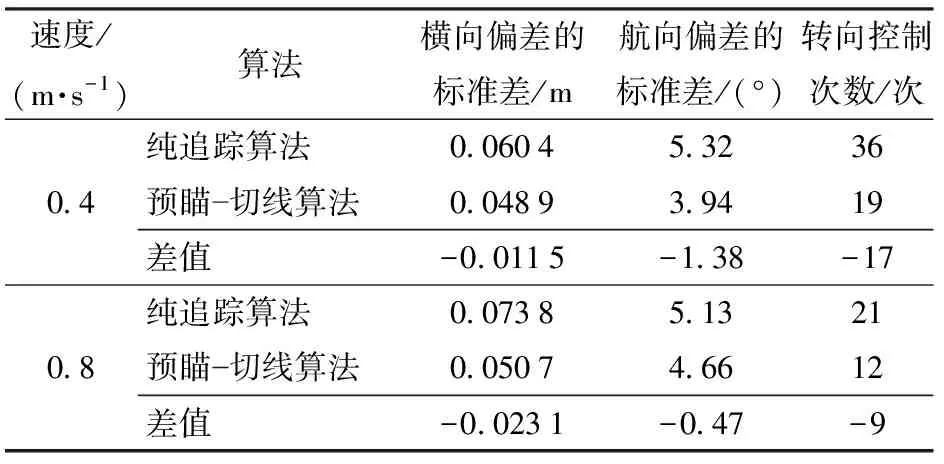
第1次转向利用预瞄点快速逼近期望路径:预瞄点M1在1/2横向偏差线GE2上,线段OM1长度为前视距离Ld;设转向圆弧的圆心为点Oc1,第1次转向半径为Rc1。收获机通过第1次转向到达预瞄点M1(设实际到达位置为点M′1),此时直线M′1H为收获机当前航向,航向偏差为θe2。横向偏差为线段M′1N2长度即de2。若de2 图2 局部跟踪路径规划及导航控制算法流程图 广泛应用于车辆局部跟踪路径规划的纯追踪模型是一种基于车辆运动学模型的模拟人工驾驶行为的几何计算方法,通过计算车辆位姿与期望路径之间的数学关系得到车辆逼近预瞄点的弧线路径[23-25],如图3所示。 图3 纯追踪模型几何示意图 车体坐标系xOy下,1/2横向偏差线为NM,预瞄点M坐标为(x′,y′),线段OM长度为前视距离Ld;线段ON长度为横向偏差de1/2;OE与NM平行,航向偏差为θe1;点Oc为转向圆弧的圆心,线段OOc长度为转向半径Rc1,线段OcQ的长度为l。规定横向偏差de偏左为负、偏右为正,航向偏差θe偏左为负、偏右为正。由图3中的几何关系可知 (1) 由式(1)得第1段圆弧转向半径为 (2) 由式(2)可知跟踪路径圆弧半径Rc1由前视距离Ld、横向偏差de1和航向偏差θe1共同决定。由图1易知第2次转向后,轨迹圆弧与期望路径相切,可得第2段圆弧转向半径为 (3) 收获机逆时针转向时的转向半径Rc1、Rc2为正,顺时针转向时为负。 模糊控制器对非线性系统控制和专家经验知识的表达效果显著,尤其在复杂农田作业场景中应用广泛[26]。为了确定联合收获机在不同位姿状态的前视距离,本文以横向偏差和航向偏差作为模糊控制器的输入,前视距离作为输出。横向偏差de基本论域为[-0.6 m,0.6 m],量化等级为{-1,-0.5,0,0.5,1}={NB,NS,ZO,PS,PB},量化因子为5/3;航向偏差θe基本论域为[-20°,20°],量化等级为{-1,-0.5,0,0.5,1}={NB,NS,ZO,PS,PB},量化因子为1/20;前视距离基本论域为[1 m,5 m],量化等级为{0.2,0.4,0.6,0.8,1}={S,M,Z,L,BL},量化因子为1/5。采用三角隶属度函数对变量进行模糊化,利用加权平均法进行反模糊化。模糊控制规则如表1所示,模糊控制曲面如图4所示。 表1 模糊控制规则 图4 模糊控制曲面 图5 局部跟踪路径规划策略 (4) 为验证本研究提出的预瞄-切线局部跟踪路径动态规划算法的控制效果,利用Matlab 2020b软件分别对本算法和传统纯追踪算法的上线过程进行仿真对比分析。设期望路径为直线Y=0,收获机位姿状态更新方程为 (-Ri-1) (5) 式中i——收获机姿态序号 Xi——第i个姿态位置横坐标 Yi——第i个姿态位置纵坐标 θei——第i个姿态航向偏差 Ri-1——第i-1次的转向半径 v——前进速度 T——转向控制周期 为便于比较,前视距离Ld均设置为2.5 m,前进速度v为1.0 m/s,结合收获机转向控制瞬态响应特性设置转向控制周期T为1.0 s,收获机状态观测周期为0.2 s。当横向偏差满足条件de(i-1)dei≤0则认为收获机上线,程序结束运行。分别进行两组仿真对比试验,记录收获机上线时的姿态信息,试验结果如图6和表2所示。 表2 仿真试验结果 仿真试验结果表明,初始位姿条件为X0=-0.5 m、Y0=0 m、θe0=-15°以及X0=-1.0 m、Y0=0 m、θe0=5°时,预瞄-切线法只需转向2次,转向控制次数比传统算法减少50%以上,收获机上线时的横向偏差和航向偏差均小于传统纯追踪算法。仿真结果表明,预瞄-切线局部跟踪路径动态规划算法原理上可行,满足跟踪精度高和转向控制次数低的要求,可以用于导航路径跟踪控制。 自动导航系统根据路径跟踪策略计算得出的速度控制参数V和转向控制参数K,分别等效于收获机手动操作模式下,前进操作手柄和转向操作手柄产生的模拟量电压信号值。工控机通过CAN通讯的方式,将控制参数传输给车载控制器作为输入信号对电控液压系统实施控制,分别实现行走和转向动作。控制参数相同条件下,履带式农机在不同地况条件下的沉陷、滑转、滑移程度均有较大差异,尤其在地况参数未知的情况下,无法直接建立与农机转向特性相适应的控制模型。当局部跟踪路径确定后,获得适应于收获机转向特性的转向控制参数尤为关键。 为了得到转向控制参数K与转向半径R、前进控制参数V之间的关系,本研究在同一地块土壤物理特性相近的前提条件下,通过田间试验的方法获得上述参数之间的数学关系,建立与收获机实际转向特性相适应的转向控制模型。前期单因素试验发现,转向控制参数K与转向半径R呈自然对数函数关系(V=6 813 mV),如图7所示。 图7 转向控制参数与转向半径的关系 为探究收获机实际前进速度v与前进控制参数V之间的关系,收获机保持直行状态下进行单因素试验,每组重复3次,结果取平均值,试验结果如图8所示。分别利用线性函数、二次函数、三次函数和对数函数进行最小二乘拟合,拟合决定系数R2分别为0.970 7、0.970 7、0.993 4、0.963 7,在前进控制参数有效范围内,三次函数拟合精度最高,拟合方程为 图8 前进速度与前进控制参数的关系 v=-4.629×10-11V3+9.84×10-7V2- 0.006 53V+13.874 (6) 当前进速度一定时,履带与地面存在滑移、滑转现象,车辆实际转向半径大于理论转向半径,且随着前进速度的增大,转向半径也随之增大。因此,收获机导航跟踪路径圆弧确定后,实际转向控制时需要通过改变转向控制值减小转向半径,补偿因侧滑导致的曲率减小量[27]。设收获机前进速度控制参数与转向控制参数呈线性关系,综合上述分析构建转向控制数学模型 K(R,V)=alnR+bRV+cV+d (7) 式中a、b、c、d——转向控制模型系数 田间实测数据集合为{(Ki,Ri,Vi)}(i=1,2,…,n),利用最小二乘法对转向控制模型曲面方程进行拟合,建立目标函数 (8) 式中n——实测数据总组数 (9) 通过矩阵运算可求解出目标函数的各项系数,从而得到转向控制数学模型。 转向过程中,将实时采集到的联合收获机在世界大地坐标系(WGS84)下的经纬度位置信息转换为笛卡尔直角坐标系下的位置坐标(xi,yi),存储在动态数组[p(x1,y1),p(x2,y2),…,p(xnc,ync)]中,转向完成后得到nc个坐标数据{(xi,yi)}(i=1,2,…,nc)。利用最小二乘法对离散样本点进行圆弧拟合,设拟合圆的一般方程为 x2+y2+Ax+Bx+C=0 (10) 式中A、B、C——拟合圆方程系数 转向半径R和拟合精度η分别为 (11) (12) 式中di——样本观测点到拟合圆圆心的距离 为进一步验证本研究提出的局部路径跟踪控制算法的有效性,基于中联重科PL60(4LZT-6Z)型履带式联合收获机进行电控化改装,构建了导航路径跟踪控制试验平台。履带式联合收获机主要技术参数如表3所示。 表3 履带式联合收获机主要技术参数 导航控制系统结构如图9所示,主要由位姿传感器、人机交互终端、工控机和车载控制器组成。位姿传感器由高精度RTK-GNSS定位装置(P3-DU型,上海华测导航技术股份有限公司,位置精度±(10+1×10-6D)mm,其中D为接收机与基站的距离(km),航向精度0.2°,测速精度0.03 m/s,数据采集频率5 Hz)和惯性传感器(MTi30型,荷兰Xsens公司,横滚姿态精度±0.2°)组成,为工控机提供履带式联合收获机位置和姿态信息。人机交互终端用于自动导航作业参数设置和实时显示收获机的运行状态等。工控机(UNO-2484G型,研华科技有限公司)主要用作路径规划、自动导航程序的运行和数据记录保存等。车载控制器通过CAN总线接收工控机发出的控制指令对比例电磁阀进行控制,完成转向和行走等动作。自动导航系统软件在Visual Studio 2019集成开发环境中使用C#语言基于Windows窗体应用程序开发。 图9 导航控制系统结构框图 为进一步验证本文算法在田间实际跟踪的实用性,在2021年11月利用试验平台进行了转向性能试验和直线导航跟踪控制对比试验,试验场地为苏州市临湖农业专业合作社平整稻茬田,稻茬平均高度9.87 cm,土壤含水率为51.22%,坚实度为612.84 kPa,试验现场如图10所示。 图10 履带式联合收获机田间试验 试验前,利用人机交互终端设定转向控制参数K和行走控制参数V,为了避免收获机启动前进时的抖动误差,令收获机直行3 s运行平稳后再进行自动转向,并实时记录位置数据。利用2.2节方法对转向过程中的轨迹点进行圆弧拟合和半径计算。收获机转向性能试验过程中运动轨迹和圆弧拟合结果如图11所示。 图11 联合收获机运动轨迹及圆弧拟合结果 转向运动特性的试验方案和结果如表4所示,通过最小二乘法得到的左转、右转控制模型分别为 表4 转向特性试验方案和结果 KL(R,V)=285.34lnR-0.055V+2 675.185 (13) KR(R,V)=-261.04lnR+0.023V+7 675.169 (14) 模型拟合的决定系数R2分别为0.978和0.980,表明拟合效果较好,可以用于收获机导航路径跟踪控制,模型三维曲面如图12所示。由转向控制模型可知,转向控制参数与转向半径呈自然对数关系,与前进控制参数呈线性关系。由于加工制造误差、部件磨损等原因,通常会造成左、右转向系统存在一定的结构非对称差异,因此基于收获机转向运动特性生成的转向控制模型在一定程度上可减小控制误差,更加符合收获机实际运动规律,有利于提高导航路径跟踪精度。 图12 转向控制参数与转向半径、前进控制参数之间的关系 分别利用传统纯追踪算法和本文算法进行25 m直线导航跟踪试验,初始位置的横向偏差为-0.25 m、航向偏差为20°。依据实际作业工况,前进速度设定为0.4 m/s(V=6 765 mV)、0.8 m/s(V=7 696 mV),允许横向偏差设置为0.025 m,每组试验重复3次,第2次直线路径导航跟踪试验效果如图13、14所示。 图13 路径跟踪偏差对比结果(v=0.4 m/s) 图14 路径跟踪偏差对比结果(v=0.8 m/s) 根据试验结果,路径跟踪过程可归纳为3个阶段:第1阶段,收获机横向偏差较大时,为了快速逼近期望路径,会以较小的半径转向运动,两种算法此阶段的横向偏差和航向偏差变化幅度均较大;第2阶段,当收获机临近期望路径时,其横向偏差较小,但还存在较大的航向偏差,此阶段需要以较小的转向半径运动使得横向偏差变化较小的同时迅速减小航向偏差,以达到上线的目的,本文算法比传统算法上线效率更高;第3阶段,收获机上线后的横向偏差和航向偏差均在小范围内波动,以较大的转向半径运动进行微调纠偏,从而达到稳定跟踪的目的,本文算法比传统算法跟踪稳定性更高。 对比两种算法的直线路径跟踪效果,试验结果均值如表5所示,当前进速度为0.4、0.8 m/s时,本文预瞄-切线算法与传统纯追踪算法结果相比,横向偏差的标准差分别减小19.04%、31.30%,航向偏差的标准差分别减小25.94%、9.16%,转向控制次数分别减少47.22%、42.86%。表明本文提出的预瞄-切线算法在导航精度和控制过程的稳定性均优于传统算法。且本文算法的转向控制频率较传统算法大幅降低,对减小制动部件磨损、降低液压系统振荡冲击、延长农机使用寿命等有明显优势。 表5 路径跟踪试验结果对比 (1)为降低履带式联合收获机导航路径跟踪控制频率和提高控制系统的稳定性,提出了一种预瞄-切线局部跟踪路径动态规划算法,该算法控制思路简洁清晰,易实现。 (2)通过分析转向控制参数、前进控制参数和转向半径之间的关系,基于收获机实际转向运动特性建立了转向控制数学模型,左转、右转控制模型拟合的决定系数R2分别为0.978、0.980。转向控制参数与转向半径呈自然对数关系,与前进控制参数呈线性关系。 (3)构建了导航路径跟踪控制试验平台,田间试验表明:利用本文算法进行跟踪控制,当前进速度为0.4、0.8 m/s时,横向偏差的标准差分别为0.048 9、0.050 7 m,航向偏差的标准差分别为3.94°、4.66°,转向控制次数分别为19、12次;与传统纯追踪算法相比,横向偏差的标准差分别减小19.04%、31.30%,航向偏差的标准差分别减小25.94%、9.16%,转向控制次数分别减少47.22%、42.86%。说明本文提出的预瞄-切线局部跟踪路径规划算法整体优于传统纯追踪算法,有效降低了转向控制频率,且提高了路径跟踪精度和控制系统的稳定性。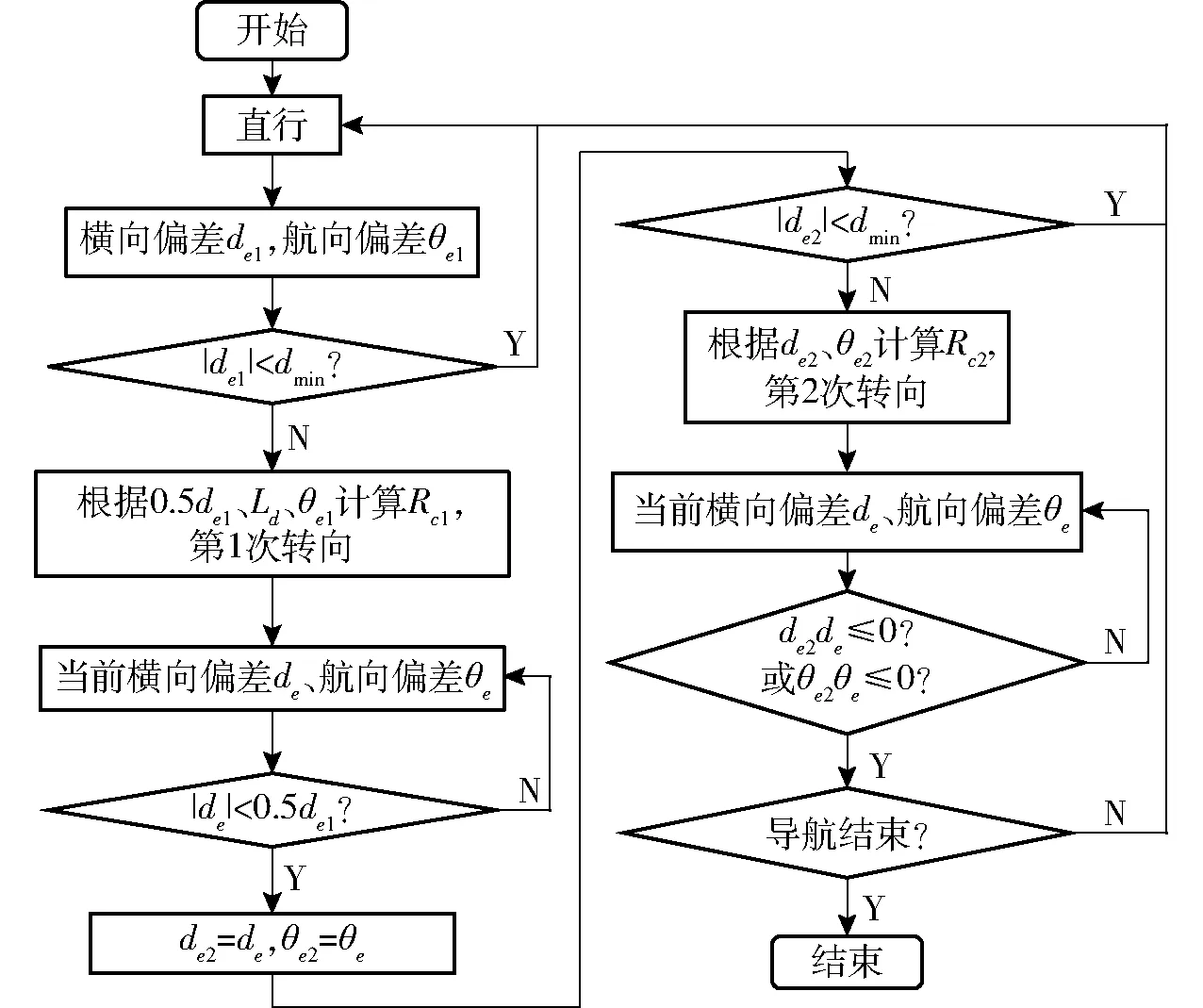
1.2 跟踪弧线半径确定

1.3 前视距离动态调整


1.4 跟踪路径切线圆弧半径确定
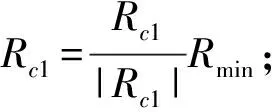
1.5 仿真对比分析
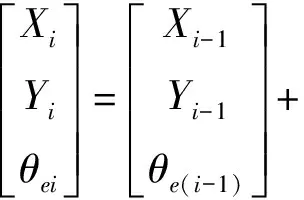


2 转向控制模型构建
2.1 转向控制模型构建方法

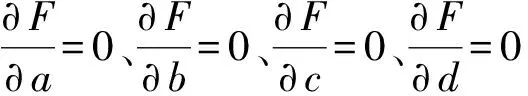
2.2 实际转向半径测算
2.3 试验平台构建


3 田间试验
3.1 转向运动特性试验




3.2 直线导航跟踪对比试验


4 结论
———2020 款中农博远玉米收获机值得期待

