初支混凝土硬化特性与围岩流变耦合作用机制
刘 昌,张顶立,孙振宇,张素磊,方黄城,李 然
(1. 北京交通大学城市与地下工程教育部重点实验室,北京 100044;2. 青岛理工大学土木工程学院,青岛 266033)
深埋软岩隧道开挖具有显著流变效应,围岩变形表现出明显时间效应[1]。隧道施工纵向掘进空间效应及喷射混凝土硬化特性随时间不断调整,导致“支护-围岩”动态作用关系错综复杂。目前,喷射混凝土广泛应用于隧道工程,然而,既有关于深埋圆形隧道黏弹性解析均忽略了喷射混凝土硬化特性,导致对软岩隧道初期支护施作早期隧道结构力学演化机制尚存在诸多疑惑,而此阶段安全事故频发现状也给隧道施工带来极大挑战[2]。
现阶段流变岩体隧道开挖主要考虑两方面时效特性:一是围岩流变效应,二是隧道纵向掘进空间效应。20 世纪70 年代—90 年代至今,国内外学者便开展了地下工程围岩应力释放现象研究,SHUNSUKE[3]、孙钧等[4]和PANET 等[5]先后指出应力释放效应与距掌子面距离等因素有关,并给出了应力释放系数与隧道开挖半径、掘进速度、距掌子面距离的关系式。近年来,应力释放系数被引入到流变岩体隧道开挖问题的解析模型中来,SULEM等[6]、NOMIKOS 等[7]、LIN 等[8−9]、KARGAR 等[10]、DO 等[11]、ARORA 等[12]、CHEN 等[13]和吴奎等[14]学者对此开展了一系列解析,但研究重点主要放在围岩流变效应对支护结构力学特性影响机制上,均未考虑支护结构材料时变特性对“支护-围岩”相互作用关系的影响。
喷射混凝土作为初期支护重要组成部分,具有显著硬化特性,一直以来是学术界研究热点。ORESTE 等[15]和PAN 等[16]研究发现,隧道设计应考虑喷射混凝土强度随时间增长的硬化因素,因隧道初期支护的临界破坏,大多发生在喷射混凝土达到其极限强度之前;ORESTE[17]基于收敛约束法考虑了喷射混凝土刚度逐渐增大的特性,通过迭代算法得到了喷射混凝土的支护特性曲线,并对其安全性进行了探讨;常燕庭[18]和孙振宇等[19]基于弹塑性理论建立了考虑喷射混凝土硬化特性的解析模型,并对初期支护施作时机作了初步探讨;此外,GRAZIANI 等[20]、张德华等[21−22]、黄明利等[23]和徐全等[24]依托数值计算软件,通过改变不同开挖阶段喷射混凝土弹性模量来实现硬化过程,就其硬化特性对其力学特性影响规律进行了分析。综上可知,喷射混凝土早期硬化特性显著影响隧道结构力学特性及安全性。然而既有关于喷射混凝土硬化特性的研究均是将围岩考虑为弹性或弹塑性,对于软弱流变岩体情况未有提及。
软弱岩体隧道开挖后围岩荷载具有显著时间效应,这与弹(塑)性地层围岩荷载变化规律截然不同[25−28]。鉴于喷射混凝土刚度增长速度明显大于其强度增长速度,某一时刻喷射混凝土承担荷载可能高于当前极限承载能力而失效[15−19],因此喷射混凝土支护时机及硬化特性对隧道结构安全性具有重要意义。此外,型钢钢架及格栅钢架作为主要初期支护类型,被广泛应用于隧道工程,两者适用性及施工阶段力学演化特性一直是关注的重点[29−31],目前关于黏弹性隧道围岩与喷射混凝土+钢架支护系统的相互作用尚缺乏合理、有效理论解析,给隧道设计带来诸多困难。理论解析方法虽然对研究问题进行了一定简化,但相比于数值仿真及模型试验,可更深入、更方便地揭示相关参数对结构力学演化过程影响规律,可为隧道工程提供初步设计。
综上所述,本文基于围岩黏弹性本构模型,建立考虑隧道掘进空间效应、喷射混凝土硬化特性及围岩流变效应的“支护-围岩”耦合解析模型,获取围岩变形、支护力动态演化规律,并与数值计算结果对比验证。就喷射混凝土设计参数、工程参数、围岩流变特性等对“支护-围岩”动态作用影响机制进行了敏感性分析;最后通过具体实例,探讨了喷射混凝土+型钢钢架与喷射混凝土+格栅钢架支护时效特性,并给出了合理支护时机,研究成果可为软岩隧道初期支护设计提供理论参考。
1 力学模型
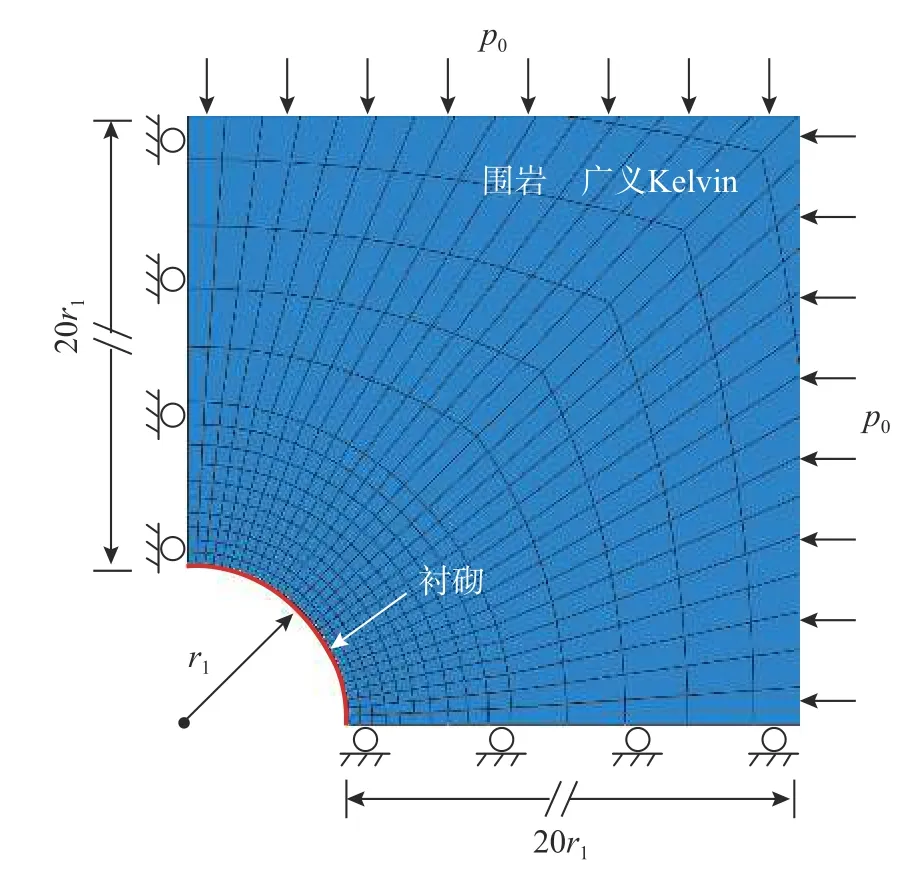
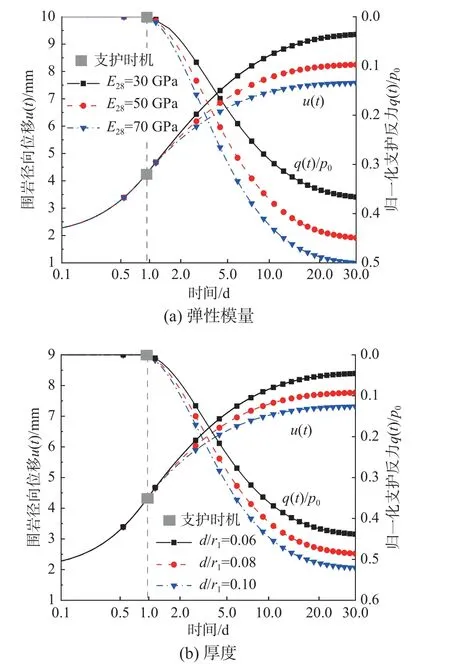
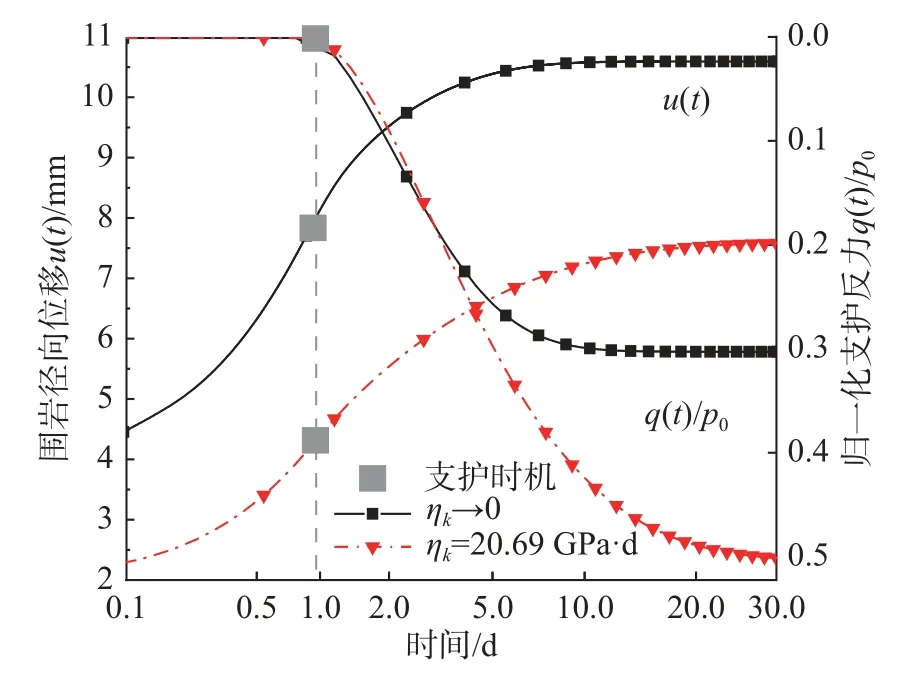
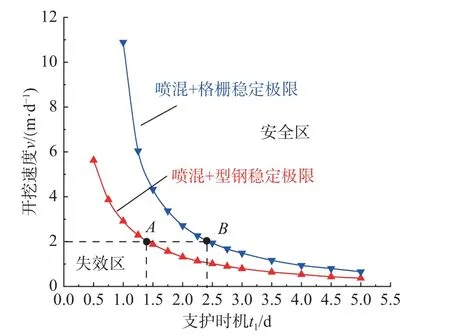
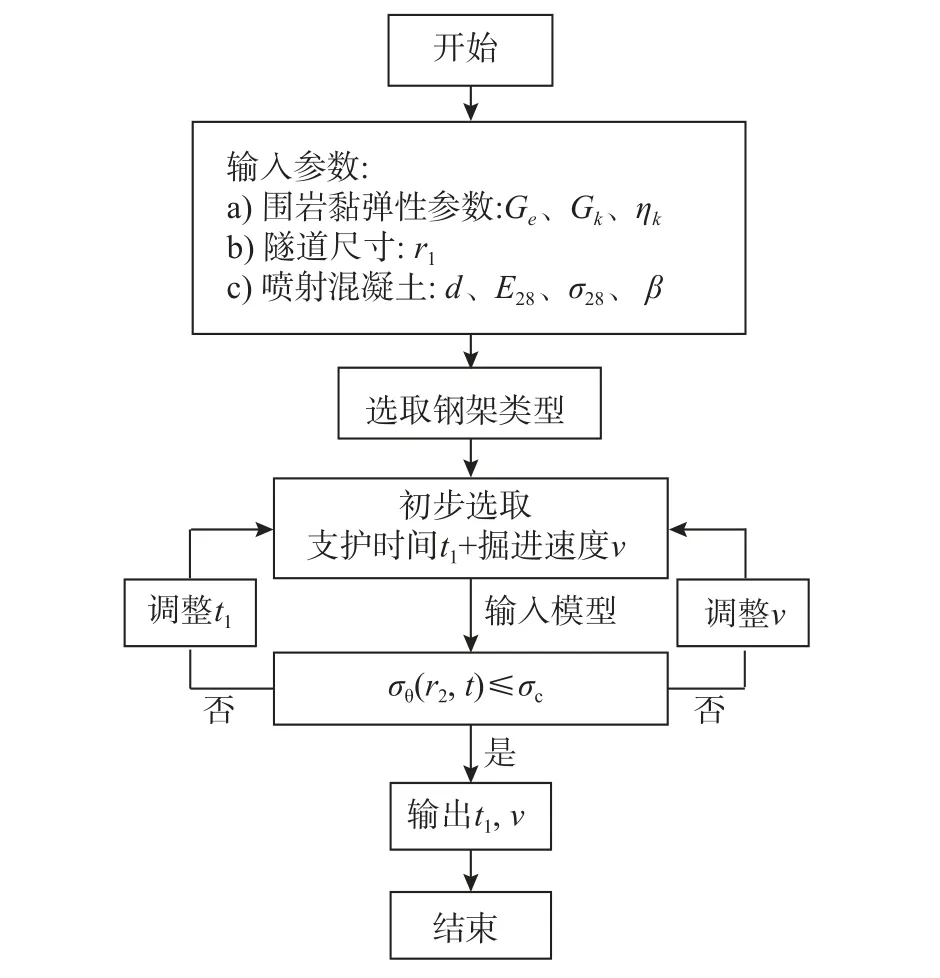
深埋圆形隧道开挖、支护过程中力学特性演化过程见图1。假定围岩为各向同性均匀黏弹性岩体,无穷远处受初始地应力p0作用,q(t)为支护与围岩间作用力,r1为隧道开挖半径,r2为支护结构内径,支护厚度用d表示。隧道开挖对围岩扰动具有显著时空效应,开挖面附近围岩流变荷载渐进释放,假设隧道在t=0 开挖,t=t1施作初期支护,由图1 可将“支护-围岩”动态演化过程分为3 个阶段:1)t 图1 支护-围岩动态演化模型Fig. 1 Dynamic evolution between support and rock mass 为将隧道纵向开挖三维空间问题等价为二维平面应变模型,采用虚拟支护力p1(t)对隧道纵向掘进空间效应进行等效,p1(t)表示为[32]: 式中,λ(t)为围岩应力释放系数,表达式为: 式中:1−α 为隧道开挖瞬间应力释放率;m=3.15v/2r1,v为隧道掘进速度。 喷射混凝土施作后,在一系列水化反应、凝结硬化后其力学特性显著增强。目前,关于喷射混凝土施作早期刚度、强度的研究成果较为丰富,既有研究表明使用与龄期有关的弹性模型描述喷射混凝土的早性质是可行的[15−24]。既有研究表明:时间指数函数能较好的表征喷射混凝土硬化特性,则喷射混凝土弹性模量及强度时变特性可由式(3)给出[15,17,21−24,33]: 式中:t/h 为龄期;β/h−1为弹性模量硬化时间系数;χ/h−1为强度增长时间常数;E28、σ28分别为t=28 d 时的弹性模量、抗压强度,泊松比在硬化过程中可假设为常数,等于0.2。 假设黏弹性围岩的畸变形满足图2 所示的广义Kelvin 本构模型,其三维黏弹性本构方程为[34]: 图2 广义Kelvin 本构模型Fig. 2 The Generallized Kelvin constitutive model 式中:sij、eij分别为偏应力、偏应变;σii、εii分别为体应力、体应变;Ge、Gk为胡克体剪切模量;ηk为黏壶粘滞系数。 在单位荷载sij=s0H(t)下,对式(4)进行拉氏变换得应变偏量在拉氏空间表达式为: 然后,对式(5)进行拉氏逆变换得eij=J(t)s0,其中J(t)为三维蠕变柔度,由式(6)给出[34]: 按照上述求解过程,即可得到考虑喷射混凝土硬化特性条件下围岩位移,uR-L(tk)=y1(tk),然后根据式(12)、式(13)、式(16)可求出支护反力。 为验证解析模型,采用FLAC3D 软件建立图3所示数值模型。通过内置FISH 语言编写程序实现隧道开挖过程中应力释放及喷射混凝土硬化过程。在t=0 开挖隧道,t1=0.96 d 施作支护,则t>t1后围岩与支护结构共同变形,即实现了两者耦合效应,由于计算模型高度对称,取1/4 模型进行分析[8−9,27,36],为削弱边界效应影响,隧道两侧各取20 倍洞径范围,模型前、后、左、底部设置单向位移固定边界,右侧和顶部为应力边界,围岩、衬砌分别采用实体单元、壳单元进行模拟。围岩、支护参数取自文献[32,37],初始应力场p0=7.6 MPa,喷射混凝土硬化系数β=0.032[18,22],具体参数见表1。 图3 数值计算模型Fig. 3 Numerical simulation model 表1 围岩和衬砌参数Table 1 Parameters of surrounding rock and lining 图4 给出了本文解答与数值计算结果对比曲线,两者计算结果基本吻合,验证了本文解析模型正确性。目前,关于黏弹性岩体隧道开挖、支护的解析模型均未考虑喷射混凝土硬化特性,因此,将本文考虑喷射混凝土硬化特性的理论解答与CHU等[32]未考虑喷射混凝土硬化特性的解答进行对比,指出考虑喷射混凝土硬化特性的必要性。 图4 本文解与FLAC3D 计算结果对比Fig. 4 Comparison of presented results and FLAC3D results 由图5 可见,当不考虑喷射混凝土硬化特性时(β→∞),本文理论模型与CHU 等[32]计算结果一致;若考虑喷射混凝土硬化特性时,在支护施作初期混凝土刚度较低,支护力发展缓慢,此时围岩变形增长迅速;混凝土刚度随时间增长而逐渐提高,在围岩荷载流变效应及开挖空间效应作用下,围岩位移仍呈缓慢增长现象,而支护力较不考虑混凝土硬化特性时增长要慢。可知若未考虑喷射混凝土硬化特性,将高估了喷射混凝土支护控制围岩变形的作用;从常规支护设计角度而言,不考虑喷射混凝土硬化特性时支护结构承载能力冗余,导致结构承载能力设计偏保守。 图5 本文解与既有文献解对比Fig. 5 Comparison of presented results and existing results 喷射混凝土硬化系数β、弹性模量E28及厚度d影响隧道施工阶段结构安全性及稳定性。因此,对喷射混凝土性能及参数进行分析,有利于明确支护-围岩相互作用关系,也能指导喷射混凝土的初期设计。而对不同隧道工程参数(开挖速度、支护时机)进行参数敏感性分析,可获取合理的施工参数,指导设计、施工。分析某参数时其他参数与表1 相同。 3.2.1 喷射混凝土设计参数的影响 图6 为喷射混凝土不同硬化系数下围岩位移及均一化支护反力曲线图。可见,喷射混凝土硬化系数β 越大,混凝土初期刚度增长速度越快,有利于限制隧道围岩早期变形,但支护结构承受荷载增大。当混凝土硬化系数β ≤ 0.01 时,喷射混凝土刚度增长速度过低,承载能力不能很好匹配流变荷载的发展,导致围岩变形显著增大,因此对于软岩隧道,建议采用早强混凝土限制围岩早期变形。当喷射混凝土硬化系数大于一定值后,硬化系数的提高对限制围岩变形敏感性逐渐减弱,而支护反力逐渐增大,使得支护结构承受荷载持续增大。可见,喷射混凝土早期硬化特性对支护施作初期隧道稳定性影响较大,选择合理的喷射混凝土硬化系数对于确保隧道施工安全性及经济合理性具有重要意义。 图6 喷射混凝土硬化时间参数的影响Fig. 6 Influence of hardening time of shotcrete 图7 为喷射混凝土不同弹性模量设计值E28及厚度d下围岩位移及支护反力曲线。由图7(a)可见,E28越大同时刻喷射混凝土刚度增幅越大,能更好限制围岩变形,与此同时需要承担更多围岩应力释放荷载而导致支护力增长,上述现象随时间增长越明显。 图7(b)给出了喷射混凝土均一化厚度d/r1=0.06、0.08、0.1 时围岩位移及支护反力演化曲线。喷射混凝土越薄承载能力越弱,对围岩变形限制效果越差,支护力越小。以t= 5 d 时为例,d/r1=0.06、d/r1=0.08 时的位移比d/r1=0.1 增大了4.9%、8.8%,而支护力则降低了13%、23%,则支护力受喷混厚度的影响敏感性显著高于围岩变形。可见,一定条件下薄层支护不仅能较好限制围岩变形且对支护结构承载能力要求较低。 图7 喷射混凝土弹性模量及厚度的影响Fig. 7 Influence of elastic modulus and thickness of shotcrete 3.2.2 隧道工程参数的影响 图8 为不同支护时机t1及掘进速度v下围岩变形及支护反力曲线。 由图8(a)可见,支护时机t1越小,围岩应力释放程度越低、围岩变形越小,则支护施作后承担荷载较高;t1越大,隧道无支护时段越长,围岩应力释放程度越高,则围岩在t 图8 隧道工程参数的影响Fig. 8 Influence of construction parameters 3.2.3 围岩黏弹性参数的影响 分析广义Kelvin 模型参数对围岩变形及支护反力影响机制前,首先对其蠕变特征进行分析。式(36)给出了不考虑应力释放及支护效应的隧道开挖后围岩位移ur(t): 式中:u0为开挖瞬时位移;td= ηk/Gk为松弛时间。 由式(36)可见,Ge/Gk影响位移速率及位移终值,而td决定着黏弹性未支护隧道围岩变形稳定时间,因此,对于支护隧道也主要对Ge/Gk及td进行分析,参数Ge与表1 一致。分别对Ge/Gk与td分别为0.5、1、2 进行参数分析。图9 给出了不同Ge/Gk及td下围岩变形及支护力时程曲线。由图9(a)可见,Ge/Gk不仅影响围岩变形速率且影响最终稳定值,Ge/Gk越小同一时刻围岩变形及支护力越小,这是因为Ge/Gk越小,Kelvin 体中与黏壶体并联的胡克体刚度低,围岩流变荷载释放越慢;Ge/Gk越大围岩流变荷载越显著,因此,同一时刻围岩位移及支护力增长速率越大,最终导致围岩位移及支护力越大。图9(b)为不同松弛时间td下围岩变形及支护力时程曲线。松弛时间td越小,隧道开挖初期围岩流变荷载效应越显著,此阶段混凝土刚度较低,在较大流变荷载作用下,围岩变形及支护力增长速率越大;但松弛时间td越小、围岩稳定越早,而松弛时间td越大、围岩流变荷载释放越缓慢,围岩达到稳定时间越长,因此,松弛时间td越大,最终围岩位移越小、支护力越大。 图9 围岩黏弹性参数的影响Fig. 9 Influence of viscoelastic parameters of rock mass 当广义Kelvin 模型中黏壶体黏滞系数ηk→0时,围岩黏弹性模型退化为弹性模型,图10 为有无考虑围岩流变特性时的围岩变形及支护力曲线。 由图10 可见,不考虑围岩荷载时间效应时,喷射混凝土施作早期刚度低,在较大围岩荷载下支护结构变形速率大,而既有关于喷射混凝土硬化的研究忽视了围岩流变荷载时空效应,低估了喷射混凝土对围岩早期变形控制效果,且未考虑围岩流变效应对支护结构长期荷载效应,使得支护结构出现结构承载能力不足。相比于弹(塑)性围岩隧道,黏弹性围岩隧道初期支护的设计重点宜放在协调支护-围岩长期作用关系上。 图10 有无考虑流变特性时围岩变形及支护力Fig. 10 Rock deformation and support force with or without considering the rheological properties of surrounding rock 分析知隧道施工参数、喷射混凝土硬化特性及围岩流变特性显著影响“支护-围岩”耦合作用机制,则在隧道设计阶段考虑多因素耦合作用对于促进隧道工程精细化设计具有借鉴意义。 型钢和钢格栅是初期支护重要组成部分,两者支护效果对于维持隧道稳定性具有重要意义。支护结构选取不当会造成围岩大变形、支护结构承载能力不足等现象。如图11 所示,浙江某在建深埋软岩隧道,开挖后立即架设钢格栅支护、喷射混凝土进行封闭,之后围岩变形速率逐渐增大,导致拱部混凝土开裂,第10 d 时通过在开挖面内侧增加型钢钢架以限制围岩变形,改善了支护-围岩作用状态,避免了二次事故发生。这次事故的主要原因如下:1)初支类型选取不合适;2)支护施作时机过早,施工过程控制不当;3)在喷射混凝土施作早期支护结构刚度低,同时支护结构与围岩接触不密实,导致支护结构未能发挥应有的支护作用。 图11 支护施作不当导致结构开裂Fig. 11 Cracking of structures results from unsuitable support construction 初期支护类型、支护时机及喷射混凝土硬化特性均影响着隧道施工阶段安全性,通过一算例结合本文所建立耦合模型对型钢和钢格栅支护效果进行评价,进而指导软岩隧道设计、施工。 某隧道开挖半径4.5 m,埋深约220 m,初始地应力约为4.6 MPa;围岩采用广义Kelvin 模型,围岩参数:Ge=0.55 GPa,Gk=0.46 GPa,ηk= 4 GPa∙d;初期支护为喷射混凝土+型钢钢架或格栅钢架(图12),其中喷混E28=24.8 GPa,厚度d= 30 cm,硬化参数β = 0.035 选自现场试验,泊松比ν= 0.2。假定喷射混凝土起到封闭围岩的作用,采用等效法求解初期支护体系的等效刚度[30,38](图13): 图12 型钢钢架与格栅钢架Fig. 12 Section steel frame and grid steel frame 图13 初期支护横截面等效刚度Fig. 13 Equivalent stiffness of initial support cross section 式中:E′、A′分别为等效后支护结构等效弹性模量与横截面积;Ec、Ac分别为喷射混凝土弹性模量与横截面积;Ei、Ai分别为型钢或钢格栅弹性模量与横截面积,当i=s时表示型钢,当i=g时表示钢格栅。 型钢钢架设计参数:I20 b,间距3 榀/2 m,弹性模量200 GPa;格栅钢架设计参数:全环4 肢Φ25,间距2 榀/1m,弹性模量200 GPa,按照式(37)计算得初期支护单位长度上等效弹性模量: 图14 给出了喷射混凝土+格栅钢架支护与喷射混凝土+型钢钢架支护在支护时机t1= 0.5 d 及掘进速度v= 2 m/d 时,围岩位移及支护反力时程演化曲线。可见,格栅钢架受喷射混凝土硬化特性影响较型钢钢架显著,随喷射混凝土硬化程度提高,喷射混凝土+型钢钢架组成的复合初期支护能较好限制围岩变形,而支护力也显著高于格栅钢架。 图14 喷射混凝土硬化特性对钢架支护效果的影响Fig. 14 Comparison between H-section steel frame and grid steel frame of supporting effect 支护-围岩力学特性受支护形式、支护时机t1、开挖速度v等因素有关,为确保施工阶段初期支护不发生破坏,以支护结构是否发生塑性变形作为判定隧道是否安全条件,根据Mohr-Coulomb准则知屈服首先发生在支护结构内侧[39−40],有如下判据: 式中:σθ(r2,t)为支护结构在r=r2处的环向应力;σc为初期支护结构允许应力,便于分析对喷射混凝土+钢架复合型支护采用等效强度计算。 图15 给出了不同支护时机及开挖速度下不同支护类型的承载能力与支护力曲线对比图。支护时机及开挖速度显著影响支护结构安全性,选取合理的支护时机及施工速度是隧道结构施工安全的重要保证。既有研究[15−19]未考虑围岩荷载随时间增大这一因素,高估了支护施作初期喷射混凝土所承受荷载水平。通过大量计算发现,在开挖空间效应、流变荷载效应及喷射混凝土硬化特性耦合作用下,喷射混凝土施作初期承受荷载基本不会超过其承载能力,因此,应重点关注支护荷载增长曲线与支护最终承载能力的对比。 图15 支护结构承载能力与支护力时程曲线对比Fig. 15 Comparison between H-section steel frame and grid steel frame of supporting effect 结合本算例,以隧道开挖后围岩荷载稳定后初期支护承受荷载是否高于允许应力为评价标准,结合图16 计算流程,获取了喷射混凝土+型钢钢架与喷射混凝土+格栅钢架的支护时机与开挖速度两者间极限关系曲线(图17)。图17 中支护结构稳定极限曲线表明结构所承担荷载与支护结构强度时变曲线正好相切,因此为确保隧道初期支护结构在耦合作用下不发生结构失效,支护时机t1及开挖速度ν应满足图中关系。这里选取2 特征点对其安全性状态进行阐述,图17 中A点、B点分别是开挖速度v=2 m/d 时“喷混+型钢”、“喷混+格栅”支护体系极限关系曲线上的特征点。当采用“喷混+型钢”支护体系时,在t1> 1.36 d 时施作支护结构可确保其安全;而当采用“喷混+格栅”支护体系时,支护施作时间t1> 2.4 d 才能避免结构失效。可见,在相同掘进速度条件下,对于“喷混+格栅”支护体系的支护时机需晚于“喷混+型钢”支护体系;在同样支护时机条件下,“喷混+型钢”支护体系对于隧道掘进速度的要求要小于“喷混+格栅”支护体系,前者施工安全范围更大。 图17 支护时机与掘进速度关系曲线Fig. 17 Relationship between support time and excavation speed 综上可见,结合本文解析模型,按图16 计算流程可对黏弹性岩体中考虑应力释放及喷射混凝土硬化特性条件下初期支护类型、支护时机的选定提供初步设计。本文结合具体算例,以支护结构强度准则为依据对支护时机进行了初步探讨,未考虑围岩变形失稳层面,这也是后续研究的重点。 图16 计算流程Fig. 16 Calculation procedure 本文引入隧道掘进空间效应及喷射混凝土硬化特性,建立了考虑喷混硬化及围岩流变的支护-围岩耦合力学模型,明确了耦合作用下支护-围岩动态演化特性,并通过算例就喷射混凝土+型钢钢架与喷射混凝土+格栅钢架的支护力学时变性能进行了探讨,主要结论如下: (1)支护施作初期混凝土刚度较低,在围岩流变特性及开挖空间效应下围岩变形速率大,而喷射混凝土承担荷载较不考虑其硬化特性时要小,若不考虑喷射混凝土硬化特性,将高估了初期支护对围岩变形的控制效果,导致现有支护结构设计承载能力冗余。 (2)喷射混凝土早期硬化特性对支护施作初期隧道稳定性影响较大,流变岩体隧道宜采用早强喷射混凝土限制围岩早期变形;隧道支护时机越晚,围岩应力释放程度越高、变形越大、支护力越小;掘进速度越大,对隧道扰动时间越短,但扰动幅度大,使得围岩早期变形更显著。 (3)围岩流变荷载与喷射混凝土刚度均随时间逐渐增大,不考虑围岩流变效应会低估喷射混凝土对围岩变形控制效果及所承担荷载水平,导致支护结构后期承载能力不足,因此,流变岩体隧道初期支护设计应重视围岩长期流变荷载效应。 (4)喷射混凝土硬化特性对格栅钢架支护效果的影响较型钢钢架显著,且格栅钢架受支护时间的影响较型钢钢架更敏感。对于流变岩体隧道,在合理支护时间、掘进速度下初期支护能承担全部围岩荷载,因此,特定情况下二次衬砌作为安全储备是合理的。 (5)分析表明围岩变形及应力分布受喷射混凝土硬化特性、围岩流变效应、开挖面空间效应影响显著,是一个复杂耦合过程。本文所建立的力学模型适用于深埋软岩圆形隧道,在实际工程中应根据具体工程问题,结合以上因素合理选择支护类型及支护时机。
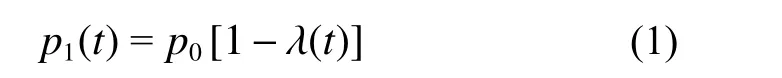






2 支护-围岩耦合作用求解过程
2.1 开挖阶段围岩位移求解
2.2 支护阶段支护-围岩耦合求解




3 模型验证及参数敏感性分析
3.1 解析模型验证



3.2 参数敏感性分析




4 初期支护选型及支护时机探讨
4.1 工程背景

4.2 喷射混凝土硬化特性对不同初期支护的影响


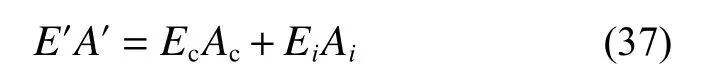


4.3 初期支护施作时机探讨


5 结论

