3D 混凝土打印进程中柱壳结构的力学性能研究

刘轩廷，孙博华

(1. 西安建筑科技大学理学院，西安 710055；2. 力学技术研究院，西安 710055；3. 西安建筑科技大学土木工程学院，西安 710055)

3D 打印的概念是由Charles Hull 于20 世纪80 年代初提出，问世至今30 余年间，3D 打印技术发展尤为迅速，并取得了巨大的成功。但当时盛行的立体光刻、熔融沉积建模方式并不适用于建筑行业，直至KHOSHNEVIS 等[1]开创性地提出了“轮廓工艺”，展现了增材制造技术在建筑领域的潜力。建筑业的增材制造方法主要是基于挤压的3D 混凝土打印(3DCP)，其中混凝土材料不断从喷嘴中挤出，以实现分层打印[2]。3DCP 技术由于材料的局限性、经济性等原因，尚未挖掘出其真正潜力，但是在某些极端条件下，有效地弥补了传统建筑的弱项，如该技术在防疫方舱医院建造方面的应用，于其他星球建造栖息地等[3−8]。

MOHAN 等 [9]针对基于挤出的3DCP 中混凝土的早期材料行为进行了讨论，将其分为了两个阶段：1)沉积前，包括将新拌混凝土运送至喷头，以及新拌混凝土由喷头挤出时，混凝土打印条的完备性，层截面几何形状等[10−14]；2)沉积后，包括3DCP 结构的建立和强度的增加。沉积后，混凝土需具备抵抗自重以及后续层重量的能力，其次3DCP 结构也需要具有足够的稳定性，因此，用于考虑3DCP 结构塑性坍塌与弹性屈曲的数值模型被讨论[15−22]。此类针对打印进程中力学性能的研究可优化打印参数的设定，同时避免大量试验。

混凝土沉积后，针对其打印进程中的力学行为，SUIKER[20]首次给出了直壁结构相应的力学模型，在引入混凝土固化性能与打印参数下，将参数模型结果与试验数据、有限元模拟进行对比分析，发现可较好地分析结构在打印进程中的破坏行为，预测直壁结构打印层数，并为找寻最佳打印参数集给予了理论指导。WOLFS 等[17]对3DCP圆柱壳结构的早期力学行为进行了数值建模与试验测试，但结果显示，有限元模拟在预测失效变形模式方面是较为准确的，但在定量分析失效层数方面仍存在提升的空间。WOLFS 等[17]将结果的差异归因于材料性能的高估以及对几何、材料缺陷的忽视。OOMS 等[22]提出并讨论了一种用于模拟3DCP 结构行为的数值模型，可用于自动生成数值分析输入文件而不管打印几何的复杂性，但在预测3DCP 圆柱壳失效层数方面仍存在较大差距。OOMS 等[22]认为结果的差异可能由材料性能的高估与有限元模拟所选的网格、单元类型导致，但其相关方面的研究并未得到较好的结果。因此，针对3DCP 进程中圆柱壳结构的力学性能进行分析是十分重要的[23]。

本文在相关壳体屈曲理论基础上[24−44]，结合打印进程参数，构建了用于描述3DCP 圆柱壳弹性屈曲与塑性坍塌的参数模型，并对二者的竞争关系进行了评判。将得出的理论、模拟结果与WOLFS 等[17]试验结果进行对比验证，发现该文提出的模型可以较好地预测3DCP 圆柱壳的失效高度与失效形式。

1 非均匀内力作用下的非均质柱壳

在3DCP 进程中，柱壳结构会因混凝土固化行为影响，材料在垂直方向(自重方向)呈非均质性。此外，柱壳结构承受的载荷为自重载荷，其应力在垂直方向同样是不均匀的。与之对应的是，需基于平衡方程与边界条件，对该非均匀内力作用下的非均质柱壳的力学模型进行描述。因此，本节通过柱壳的势能最小化原理将其压屈微分方程进行推导。

1.1 势能

如图1 所示，柱壳半径为R，高度为l，均匀厚度h。轴对称情况下，根据Goldenveizer-Novozhilov壳体理论，应变-位移关系可以表示为：

图1 柱壳在自重作用下示意图Fig. 1 Cylinder under self-weight

式中：x为纵向坐标；y为环向坐标；εx、εy、εxy为壳体中面线性应变分量；χx、χy、χxy为曲率变化；u、v、w分别为纵向、切向、径向位移。

柱壳总应变能U，由薄膜应变能Us，与中面拉伸弯曲应变能Ub组成：

其中：

式中：星号“*” 代表材料参数在空间中是非均匀的(为方便起见，取ν为常数)；E∗为非均匀弹性模量，非均匀弯曲刚度由下式给出：

1.2 平衡方程与边界条件

将式(7)进行势能最小化处理：

根据式(8)可以得到非均匀内力作用下的非均质柱壳的轴对称压屈微分方程：

2 3D 打印进程中柱壳的失效机制

如图2 所示，在3DCP 进程中可能发生两种失效机制，分别为弹性屈曲和塑性坍塌。其中当材料硬化速率与打印速率均较慢时，在结构底部容易出现较大变形，从而发生塑性坍塌。

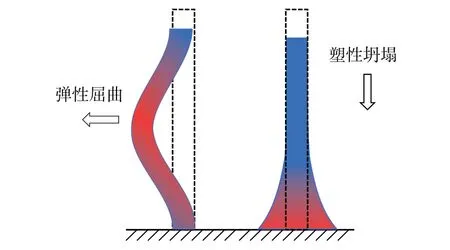
图2 3D 打印进程中失效机制示意图Fig. 2 Failure mechanism of cylinder in 3D concrete printing(3DCP) processes

在本节中建立了这两种失效机制的控制方程。弹性屈曲的控制方程可以由第1 节中所导出的压屈微分方程和边界条件所得。在引入打印材料的固化过程和印刷速度相关的时间效应影响，本节最后给出了3DCP 圆柱壳弹性屈曲与塑性破坏的竞争标准。

2.1 打印时间因素对柱壳的屈曲影响

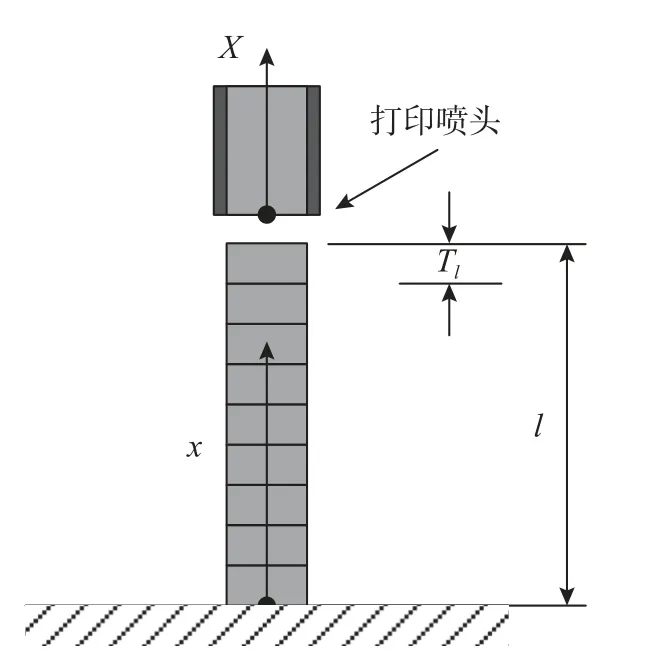
图3 柱壳打印截面示意图Fig. 3 3D printed section of a cylinder

一般情况下可以认为打印速度是固定的并设时间t=0时，l(0)=0，则存在关系l=l˙t。 这样式(12)可以简化成：

式中，t为时间。如果打印速率是变化的问题就比较复杂了， 将在今后的研究中考虑。

考虑材料在点x=0处，固化过程中弹性刚度随时间演化可表示为：

将式(17)代入式(9)、式(10)可得欧拉坐标系下无量纲屈曲方程：

其中，无量纲参数如表1 所示。

表1 无量纲参数与其物理含义Table 1 Dimensionless parameter and physical significance

2.2 柱壳的塑性破坏

除弹性屈曲外，柱壳也会因自重因素影响，达到材料塑性屈服强度 σp而发生破坏，其中的下标“ p”代表“塑性破坏”。通常来说，塑性破坏的关键位置为柱壳底部，即x=0处，此处自重产生的轴向应力达到最大值。柱壳底部塑性破坏的屈服极限强度通常可表示为：

式中：|σp|为屈服强度绝对值；l为柱壳的长度。由于固化进程因素影响，屈服强度在圆柱壳长度增长方向是不均匀的。在x轴方向，可将 σp由 σp∗代替，圆柱壳底部屈服强度随时间的变化规律可以给定为：

式中：σp,0为打印进程中t=0时刻的屈服强度；h∗(t)为屈服强度随时间演化的固化特征函数。

由于塑性屈服极限由材料所决定，即可得出与文献[20]完全相同的无量纲塑性坍塌长度随固化速率变化函数：

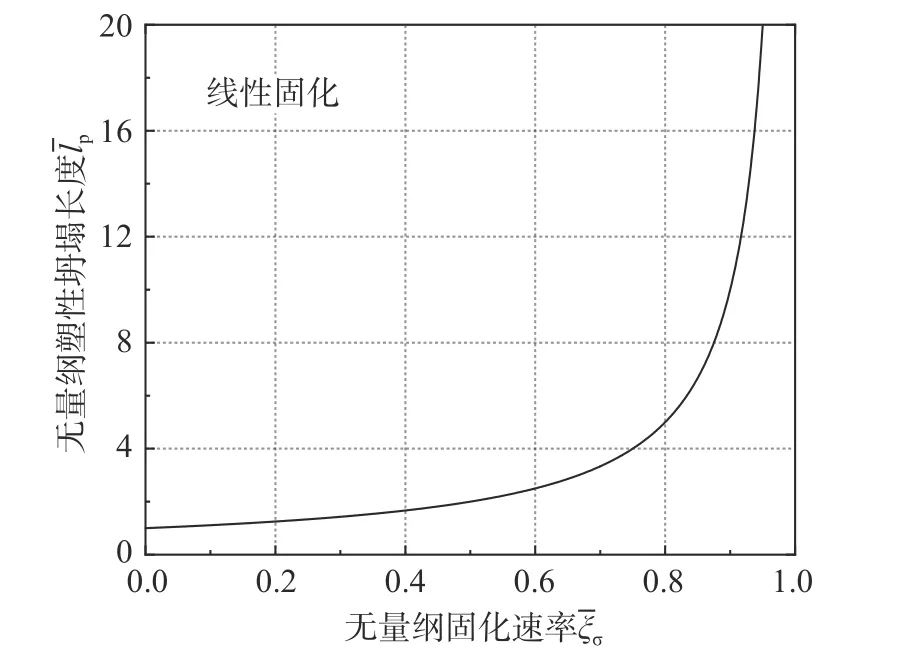
图4 塑性坍塌长度 lp 随固化速率 ξσ变化曲线图Fig. 4 Plastic collapse length lp vs. curing rate ξσ

2.3 弹性屈曲与塑性坍塌的竞争判据

当塑性坍塌长度小于弹性屈曲长度，即lplcr时，圆柱壳会发生弹性屈曲。这一用于分析可能失效机制的标准可以通过调用几何、材料和打印参数来方便地表示：

3 柱壳失效问题数值解

3.1 特征值问题的求解过程

微分方程式(18)可利用伽辽金(Galerkin)方法进行求解：

3.2 固化进程影响下数值求解分析

采用2 次、3 次、4 次、5 次多项式基函数对圆柱体分岔屈曲数值解的精度进行了评价。从图5可以看出，对于N=3 的多项式，临界屈曲长度的估计明显过高，精确性不足。对于N=4 时，精确性有所提高，但仍存在偏差。但对于N=5 和N=6，数值解在小数点后四位的结果完全相同，因此似乎已经收敛到精确解，且满足针对3DCP 圆柱壳屈曲长度分析需求。

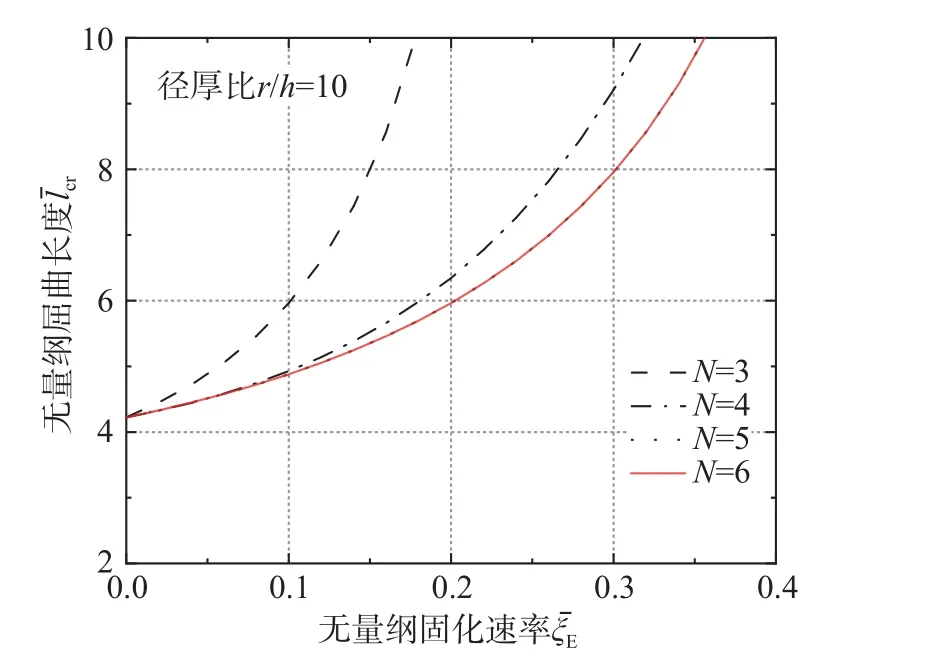
图5 无量纲屈曲长度 随无量纲固化速率 变化曲线Fig. 5 Critical buckling length vs. curing rate E

图6 3DCP 圆柱壳临界屈曲长度 lcr随固化速率 变化曲线Fig. 6 Critical buckling length vs. curing ratefor 3DCP cylinder

3.3 弹性屈曲与塑性破坏数值求解比较分析

针对柱壳弹性屈曲与塑性坍塌进行数值求解，用于分析线性固化进程中弹性屈曲与塑性坍塌的竞争关系。

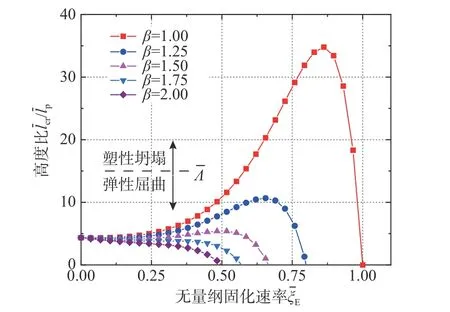
图7 3DCP 圆柱壳失效机制Fig. 7 The failure mechanism of 3DCP cylinder

3.4 实例验证

采用WOLFS 等[17]完全相同的打印参数与柱壳半径r=250 mm，打印层高tl=10 mm，打印喷头移动速度vn=5000 mm/min 。混凝土平均密度ρ=2070 kg/m3。

弹性模量方程E/kPa(t/min) ：

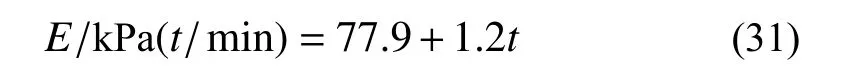
抗压屈服强度方程σp/kPa(t/min) ：

本文首先利用商用有限元软件ABAQUS 并采用与WOLFS 等[17]相同的建模方法进行模拟，得出3DCP 圆柱壳失效层数为49 层，与相关研究中的数值模拟结果相差不大。在考虑初始缺陷的影响下，采用Riks 方法进行非线性屈曲分析，缺陷幅值设为厚度的1%，得出3DCP 圆柱壳失效层数为48 层，直到设置缺陷幅值为壳厚的27.5%时，得到与试验[17]相同的失效层数，即29 层。这表明3DCP 圆柱壳存在较大的初始缺陷，但该方法很难定量分析3DCP 结构的屈曲失效行为。

在考虑到实际打印过程中层截面几何形状并非矩形[12]的情况下，采取WOLFS 等[17]相关工作中的图片目视所得结果，即圆角梯形进行模拟，层截面几何形状如图8 所示。

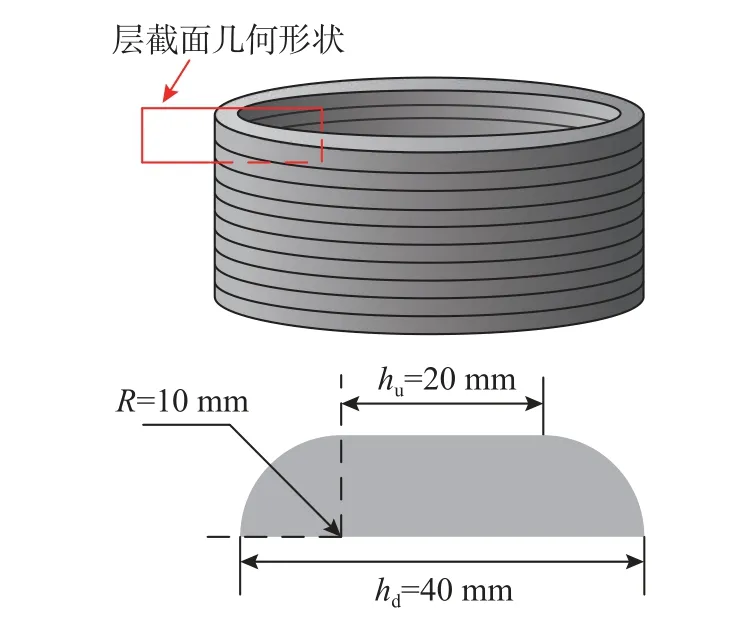
图8 3DCP 圆柱壳圆角梯形层截面示意图Fig. 8 Rounded trapezoid schematic diagram of 3DCP cylinder model

使用ABAQUS 中的RESTART 功能模拟3DCP圆柱壳的打印过程，其中分析步将采用具有更好收敛性的Dynamic、 Implicit 类型。RESTART 分析功能允许重新启动模拟并对已有的载荷历史响应进行计算，即结构的应变/位移、应力均被保留。其中每一个job 的生成代表一段物料的添加，直至模拟到结构失效。相比于目前模拟3DCP 过程的主流建模方式(MODEL CHANGE)[22]，该方法不易造成单元扭曲但计算量较大。层间接触将被建模为基于库仑-摩擦模型的法向和切向行为的组合，并假设摩擦系数为0.6[22]。选用三维实体八节点缩减积分单元(C3D8R)构建FE 网格，单层单元大约为1600 个，整个模型单元约为46 000 个。整个建模过程将利用自定义开发的参数化Python脚本进行控制。同时，利用Python 脚本对每一段打印体的材料属性进行刷新，用以模拟打印材料的时间依赖性。

如图9 所示，FEM 结果下的圆柱壳变形图将被绘制，并与WOLFS 等[17]试验结果进行对比，其中彩色点线图为模拟结果，黑色实线图为试验结果。从结果对比可以看出，模拟与试验的最大径向位移十分接近，其中FEM 结果为15.44 mm，试验结果为12.36 mm 与17.78 mm。模拟得出的破坏前结构高度为266 mm，试验结果为270.24 mm与266.42 mm。但模拟结果得出的最大径向位移点相对较低，且变形图相对较陡。这些差异可能是由于目视所得层几何形状与实际具有一定的差异，将导致屈曲模态发生变化。总体来说，更改层几何形状能得到与试验较为一致的模拟结果。同样，从径向位移云图可以看出，圆柱壳在破坏前的变形并未呈现完美轴对称情况，在结构中上部出现了不同程度的内凹现象。

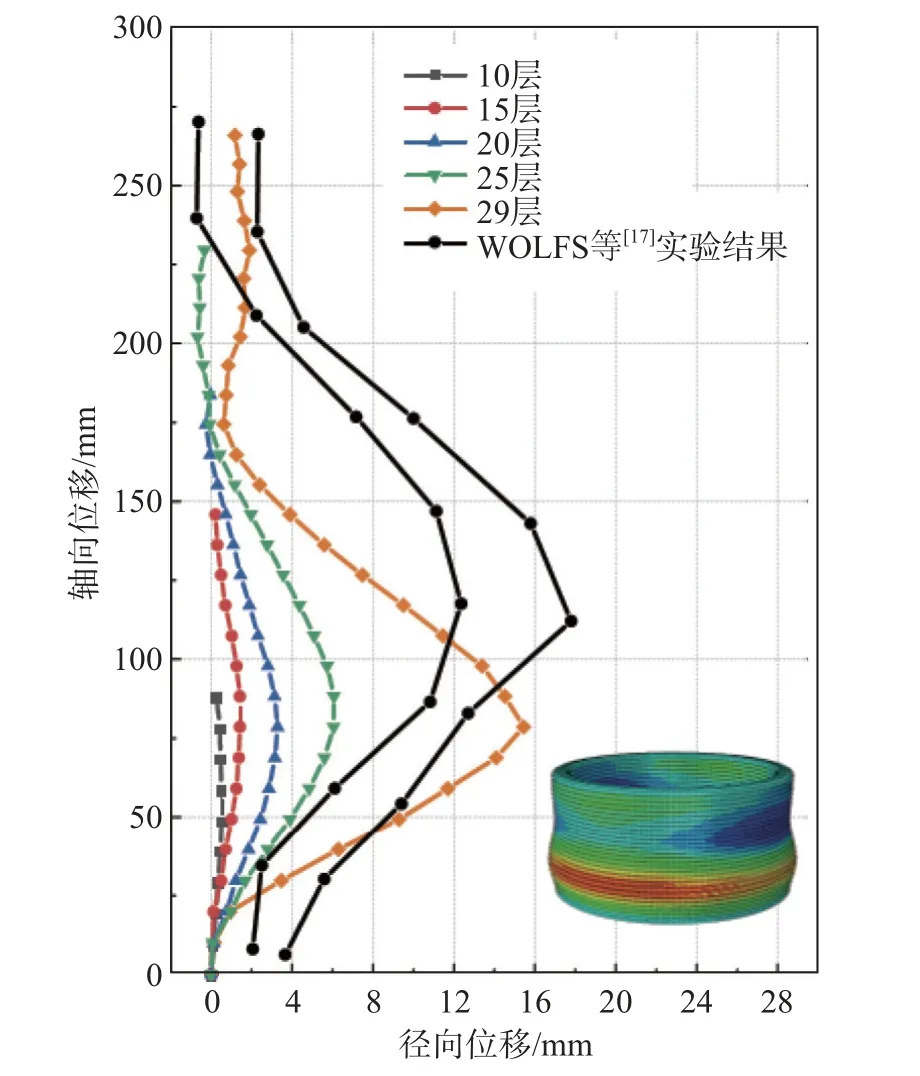
图9 FEM 与实验对比图Fig. 9 Comparison of FEM and experiment

在保证层截面几何面积一致即自重载荷不变的情况下，选取了形状为圆角矩形的情况进行有限元模拟分析，几何尺寸如图10 所示。其中，圆角半径R=12 mm ，有效壳厚为h=20.33 mm 。从结果对比可以看出，FEM 得出的最大径向位移为17.68 mm ，破坏前结构高度为283.43 mm ，失效层数为25 层。模拟与试验结果符合较好，并通过有限元对比分析可以看出，层截面的有效接触宽度为控制3DCP 圆柱壳屈曲高度的重要因素，而非测量所得的实际壳体厚度。关于层截面几何形状对3DCP 圆柱壳失效形式的影响，将在后续的工作中开展。

图10 3DCP 圆柱壳圆角矩形层截面示意图Fig. 10 Rounded rectangle schematic diagram of 3DCP cylinder model

如图11 所示，将FEM 所得圆角梯形截面的非线性屈曲分析结果与理论结果进行对比发现，理论结果相较模拟，其屈曲长度lcr较低。理论结果为25.8 层，有限元结果为29 层。二者结果之间的差异可能是因为，理论分析所得结果建立在轴对称假设下，与实际情况是存在差距的，但模拟显示3DCP 圆柱壳的变形形式将由轴对称开展至非轴对称，直至失效。但此现象开展非常迅速，在3 层～5 层内便开展完毕。因此，本文认为轴对称模型在分析3DCP 圆柱壳稳定性时，存在一定的不足，但可作为评估屈曲破坏的下限。

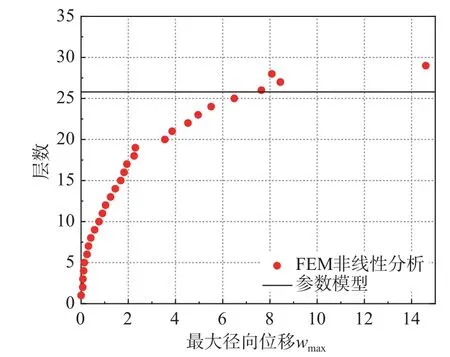
图11 最大径向位移wmax 随层高变化曲线Fig. 11 Max. radial deflection wmax vs. layer number

表2 相关工作失效层数对比Table 2 Comparison of failure layer number with related work

3.5 失效机制分析

图12 3DCP 圆柱壳无量纲失效长度l¯随径厚比 r/h变化图Fig. 12 The dimensionless failure length l¯ of 3DCP cylinders vs. the radius-thickness ratio r/h

4 结论

在本文研究中，描述了3D 混凝土打印(3DCP)圆柱壳在打印进程中的力学行为。建立了两种失效机制(弹性屈曲和塑性坍塌)的控制方程，并对这两种失效机制间的竞争关系进行了描述。最后与Wolfs 等[17]试验结果进行了对比验证。本文得出的主要结论与展望如下：

(1)建立了用于描述3DCP 圆柱壳在自重作用下的结构失效行为的数值模型，该模型可准确预测打印结构的失效高度与失效形式，这是在相关工作中均未达到的。

(2) 描述了3DCP 圆柱壳弹性屈曲与塑性坍塌之间的竞争关系，其中弹、塑性固化速率之比决定了弹性屈曲与塑性坍塌这两种失效机制的主导地位。并且在相关打印参数固定时，可以确定3DCP 结构的弹性屈曲区域与塑性坍塌区域，这为提供最优打印参数集，针对失效机制提供特定结构增强方案，减少试错性试验提供了帮助。

(3) 通过试验、模拟、理论三者结果对比分析可以看出，层截面的有效接触宽度为控制3DCP圆柱壳屈曲高度的重要因素，而非测量所得的实际壳体厚度。但仍需要对层截面几何形状以及层间界面进行更广泛的研究。