基于电压电流双环控制的蓄电池并网研究
孙思男,郝正航
(贵州大学 电气工程学院,贵州 贵阳 550025)
伴随化石能源开采程度的不断加剧,不可再生能源面临枯竭的风险,因此开发新型可循环能源[1-2]已成为研究重点。蓄电池作为备用电源,因其充放电可持续利用的特性,被广泛应用于汽车、通信、电力等行业。
在现实生产生活中,天气、闲置时间过长等因素会导致蓄电池各项性能指标不符合行业要求,因此需对蓄电池进行定期充放电实验。传统蓄电池放电采用可变电阻器作为消耗电能装置,不仅操作准确性低、可靠性差,还造成能源大量浪费。将蓄电池所释放的能量经逆变器并入大电网,不仅可以精准检测蓄电池的性能指标,还能降低电能损失,因此对蓄电池进行并网充放电具有良好的应用前景。
文献[3]通过搜集蓄电池各项参数,进行实时监控使其达到蓄电池充放电的效果,但该研究所提策略仅适用百叶窗控制,不具备推广性。文献[4]结合软硬件设计出一款蓄电池充放电检测装置,并通过实验得出电池各项性能指标,但其恒压充放电控制方式会缩短蓄电池使用寿命。文献[5]以单片机作为控制部分,并设置相应外围电路,对蓄电池充放电进行无线监测,但对蓄电池剩余容量估计不够精确。文献[6]设计了一款由直流断路器工作的蓄电池充放电控制系统,但该研究缺少实验数据。文献[7]对蓄电池充放电并网控制策略进行研究,提出了基于修正系数的非线性控制策略,但该模型较为复杂,控制效果有待进一步提高。在蓄电池并网过程中,文献[8]采用的有源滤波器虽能抑制高次谐波,但其所提出的多模式控制对蓄电池容量要求较高。文献[9]采用单片机作为控制部分并配置相应隔离电路和辅助电路,设计铅酸蓄电池充放电监控系统,可以实现对蓄电池电压和电流的有效检测,但并未充分利用充放电数据。文献[10]对系统软件和硬件结构进行了设计,并进行了多次充放电实验测试,蓄电池各项性能指标均达到预定要求,但其具体电路设计缺乏创新性。文献[11]采用数字信号处理器和晶体管设计实验装置,分析了充电装置电路拓扑结构,得出了脉冲充电理论依据。该研究虽能节省充电时间,但充电较为繁琐,增大了系统控制难度。文献[12]对汽车蓄电池进行建模,设计了一种预测电流无差拍控制方式,但大规模充放电会诱发系统谐波陡增问题,因此该模型性能仍有待进一步提升。文献[13]从电池的监测、充放电和无缝衔接等方面进行分析,绘制蓄电池充放电整体结构,实现远程充放电功能。但该研究以文字叙述为主,没有配备相应实验装置和实验数据。文献[14]对铅酸蓄电池使用寿命不长问题进行分析,提出蓄电池充放电在线监控技术,为提高电池使用寿命提供理论依据,但所提技术实用性有待进一步考证。文献[15]将蓄电池和太阳能结合,采用单片机设计充放电控制器。实验结果表明该控制器可以增强充放电系统稳定性,但直流母线电压利用率较低。文献[16]对电池硬件电路进行研究,设计出一款蓄电池充放电检测装置。该装置虽可较为准确地记录充放电效率,但研究中未对比分析所选取的不同电池产生的差别。文献[17]所提控制策略可检测蓄电池性能,但并网电流只考虑了单相情况,设置工况较为单一。文献[18~19]虽实现蓄电池在分层控制下的充放电过程,但对系统投入故障时控制策略的有效性未进行充分验证。
本文在上述研究的基础上,考虑了铅酸蓄电池真实化学反应过程,从电流、温度、电荷量3方面搭建蓄电池三阶模型。本文中,采用升降压双向变换电路控制电池充放电过程,逆变电路则采用电压电流双闭环控制,对逆变器脉冲发生信号进行空间矢量脉宽调制,系统经滤波后并入电网。在MATLAB/Simulink上进行的仿真分析结果表明,并网电流、直流母线电压以及蓄电池各项性能指标均达到预期要求。
1 铅酸蓄电池三阶动态模型
蓄电池的基本等效模型由理想电池和定值电阻构成,对电池电荷量、外界温度等因素并未考虑,故一般存在于假想状态,实用性不强。Thevenin改进模型在基本模型的基础上又加入了极化电容和过压电阻,但由于数值均为定值,并不能模拟电池内部各量的函数关系。基于以上研究,本文选用由主反应支路和寄生支路组成的三阶等效模型。与其他等效电路相比,该模型能较好地体现电池恒流充放电时端电压变化过程以及不同老化程度下蓄电池的健康状态。
1.1 铅酸蓄电池化学反应原理
铅酸蓄电池的主要结构包括电解液和正负电极板。电解液为硫酸溶液,正极板采用二氧化铅(PbO2)作为活性材料,负极板选用单质铅(Pb)作为活性材料。其充放电示意图如图1所示。

图1 铅酸蓄电池工作状态图(a)充电示意图 (b)放电示意图Figure 1. Lead-acid battery working state diagram(a)Diagram of charging (b)Diagram of discharging
蓄电池放电过程中,正极板的二氧化铅在电解液的作用下转化为硫酸铅(PbSO4)和水,负极板的铅在电解液的作用下则转变为硫酸铅和氢离子。反应方程式如下所示。
PbO2+HSO4-+3H++2e-→PbSO4+2H2O
(1)
Pb+HSO4--2e-→PbSO4+H+
(2)
蓄电池的充电过程是放电过程的逆反应过程。正负极板硫酸铅分别在水和氢离子作用下,被还原为二氧化铅和铅,其反应方程式如下所示。
PbSO4+2H2O-2e-→PbO2+HSO4-+3H+
(3)
PbSO4+H++2e-→Pb+HSO4-
(4)
1.2 铅酸蓄电池电气模型
蓄电池的电气模型由主反应支路和寄生支路组成,其结构示意图如图2所示。

图2 三阶动态电气模型Figure 2. Third-order dynamic electrical model
主反应支路包括电池开路电压Em、内阻R0、短时极化电阻R1、长时极化电阻R2、极化电容C1。开路电压与蓄电池的荷电量和电解液的温度有关。短时极化电阻和极化电容模拟了蓄电池充放电时内阻的动态反应过程。长时极化电阻与荷电量和电流有关。寄生支路为图2中寄生反应电流IP流过的支路,VPN表示寄生支路电压,整条支路模拟了充电末期水解反应对电池的影响。
由基尔霍夫电压定律可得蓄电池端电压方程
V=Em+IR0+I1R1+ImR2
(5)
由热反应理论可得蓄电池功率损耗方程。
(6)
1.3 铅酸蓄电池数学建模
铅酸蓄电池内部结构较为复杂,为准确模拟其动态过程,需对电气模型中的元件逐一列写非线性方程。蓄电池开路电压表达式为
Em=Em0-KE(273+θ)(1-SOC)
(7)
式中,Em0为电池满电状态下的开路电压;KE是电压温度系数;θ为电池电解液温度;SOC表示荷电状态。
荷电状态SOC的数学表达式为
(8)
式中,Qe表示电池放出的电量,其微分方程为

(9)
式中,Im表示主反应支路流过电池的电流;τ是时间常数,数值上等于极化电容C1和短时极化电阻R1的乘积,其物理意义为蓄电池充放电反应中电压变化的持续时间。主反应支路中极化电阻和极化电容的非线性方程为
R1=-R10ln(DOC)
(10)
(11)
C1=τ/R1
(12)
式中,R10、R20均为常数电阻;A21、A22为经验常数;I*代表电池的标称电流;DOC是电池当前容量与电池出厂容量的比值,它反映了电池的健康状态,其函数表达式为
(13)
式中,Iavg表示平均放电电流。
电池内阻R0的函数方程为
R0=R00[1+A0(1-DOC)]
(14)
式中,R00为满电量状态下的内阻;A0为经验系数。对于电池放出的总电量以及电解液的温度为
(15)
其中,θinit表示蓄电池初始温度,其物理意义为在环境温度下,长短极化电阻所消耗的功率;Ps表示热源功率;θa指蓄电池周围空气温度;Rθ为蓄电池发热电阻;Cθ为蓄电池比热容。
蓄电池总容量为
(16)
式中,ε、δ、Kc均为不同温度下测试得出的经验参数;θf表示电解液冰点温度;C0*为蓄电池在0摄氏度时的标称容量。
对于表示蓄电池充电过程中水解反应的寄生支路而言,其寄生反应电流IP和寄生电压VPN的函数关系为
IP=VPNGP0exp[VPN/VP0+AP(1-θ/θf)]
(17)
式中,GP0、VP0、AP均为经验系数。
上述所提电池三阶等效数学模型仅适用于铅酸蓄电池,对锂电池、高铁电池等其他电池模型的适用性有待进一步验证。电池模型的准确性不仅与模型适用性有关,还取决于经验参数的合理取值。本文采用最小二乘法进行参数辨识,将电流、温度、电荷量作为系统的输入,将电压为系统输出量,在电池动态系统中进行参数辨识,得到含有模型参数的差分方程,进而求出各经验参数。
根据表1电池内部参数取值情况及各参数之间的数学关系,构建蓄电池整体仿真结构图。其中模型输入量为初始SOC、电池周围环境温度θa以及充放电电流,输出量为端电压V、荷电状态SOC以及蓄电池实际容量。具体结构如图3所示。

表1 铅酸蓄电池内部参数取值情况

图3 蓄电池仿真模型结构图Figure 3. Structure diagram of battery simulation model
2 蓄电池并网控制策略
2.1 电压电流双闭环控制
因蓄电池自身控制采用比例积分环节较为简捷,故不再单独讨论。本章节主要介绍基于电压电流双闭环的蓄电池并网控制,其并网结构如图4所示。

图4 三相并网逆变器主电路拓扑图Figure 4. The topology diagram of three-phase grid-connected inverter main circuit
图4中Udc表示直流母线电压,C为电路支撑电容,Va、Vb、Vc为逆变器输出三相电压,La、Lb、Lc为滤波电感,ia、ib、ic为逆变器输出三相电流,Ra、Rb、Rc为滤波电感中的串联电阻,Ua、Ub、Uc为电网电压。由于图4三相逆变器数学模型较为复杂,故在理想条件下,将其等效为3个单相逆变器并网,具体结构如图5所示。

图5 三相逆变器等效电路结构图Figure 5. Three-phase inverter equivalent circuit structure diagram
根据图5结构,由基尔霍夫电压定律可得
(18)
针对式(18)三相abc静止坐标系下的矩阵方程,将其改写成两相静止αβ坐标系矩阵方程。
(19)
为实现电流无静差调节,需将两相静止αβ坐标系下的矩阵方程转变成两相旋转dq坐标系数学方程
(20)
(21)
式中,ω为旋转角速度,对两式分别进行拉普拉斯变换,可得逆变器在dq坐标系下的传递函数表达式为
(sL+R)Id(s)=Vd(s)-Ud(s)+ωLIq(s)
(22)
(sL+R)Iq(s)=Vq(s)-Uq(s)-ωLId(s)
(23)
针对式(22)、式(23)中+ωLIq(s)和-ωLId(s)两个耦合量,本文引入-ωLIq(s)和+ωLId(s)进行前馈解耦,以降低调节器设计难度。具体控制结构如图6所示。

图6 逆变器前馈解耦示意图Figure 6. Schematic diagram of inverter feedforward decoupling
基于以上对逆变器物理结构和数学模型的分析,得到其控制框图。具体流程如图7所示。

图7 逆变器电压电流双闭环控制Figure 7. Inverter voltage and current double closed loop control
2.2 空间矢量脉宽调制
空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)是用6个相差60°的非零矢量和两个方向相反的零矢量,通过特定时间比例和角度的组合来模拟逆变器的8种工作状态,进而控制桥臂的通断,达到逆变器输出三相电压的目的。其电压空间矢量结构如图8所示。

图8 电压空间矢量图Figure 8. The diagram of voltage space vector
SVPWM实现控制输出分3步完成:
步骤1空间矢量扇区的判断。通过Ua、Uβ的之间的函数表达式,确定电压矢量所在扇区。此处定义
x1=uβ
(24)
(25)
(26)
y=sign(x1)+2sign(x2)+4sign(x3)
(27)
式中,ua、uβ为两相静止坐标系下的电压矢量;sign为符号函数。进一步可得函数值y与扇区对应关系,如下表2所示;

表2 函数值y与扇区对应关系
步骤2计算矢量作用时间及矢量切换点。根据扇区划分,由定义计算式得出矢量作用时间和切换点数学表达式。此处定义
(28)
(29)
(30)
式中,Ts为开关周期;Udc为直流母线电压。根据扇区的位置,得出各个扇区基本矢量作用时间Tx和Ty。具体取值如表3所示。

表3 不同扇区基本矢量的作用时间
特别地,当Tx与Ty的和大于Ts时
(31)
(32)
对于矢量切换点的定义如下
Ta=(Ts-Tx-Ty)/4
(33)
Tb=Ta+Tx/2
(34)
Tc=Tb+Ty/2
(35)
步骤3确定发送时刻。对切换点进行状态赋值,通过与等效三角波对比,改变波形状态,进而实现SVPWM。
依据扇区不同,将参数Ta、Tb、Tc赋值给开关时间Tcm1、Tcm2、Tcm3。具体赋值情况如表4所示。

表4 不同扇区开关时间赋值表
选取频率为1/Ts,幅值为Ts/2的三角波与开关时间Tcmx进行比较,当两者相等时,改变调制波工作状态,进而输出脉冲开关信号。
3 仿真分析
为了验证铅酸蓄电池的充放电性能、直流母线电压以及并网电流情况,利用MATLAB/Simulink构建三阶蓄电池并网充放电模型。其仿真结果如下。
3.1 蓄电池剩余容量为30%时
3.2 蓄电池剩余容量为60%时
3.3 蓄电池剩余容量为90%时
图9~图17模拟了蓄电池在不同老化程度下的健康状态、电池内阻以及端电压变化情况。仿真时间为2 s,前0.8 s为放电时间,后1.2 s为充电时间。观察图9、图12、图15可以看出,当剩余容量不同时,蓄电池仍能正常进行充放电过程。对比图10、图13、图16可以看出,当剩余容量增大时,蓄电池内阻随之增大,符合式(14)的变化规律。对比图11、图14、图17可以看出,当剩余容量增大时,蓄电池端电压随之增大,符合式(7)的变化规律。

图9 蓄电池剩余容量为30%时蓄电池的健康状态Figure 9. The state of health of the battery when the remaining capacity of the battery is 30%

图10 蓄电池剩余容量为30%时蓄电池的内阻Figure 10. The internal resistance of battery when the remaining capacity of the battery is 30%

图11 蓄电池剩余容量为30%时蓄电池的端电压Figure 11. The terminal voltage of battery when the remaining capacity of the battery is 30%

图12 蓄电池剩余容量为60%时蓄电池的健康状态Figure 12. The state of health of the battery when the remaining capacity of the battery is 60%

图13 蓄电池剩余容量为60%时蓄电池的内阻Figure 13. The internal resistance of battery when the remaining capacity of the battery is 60%
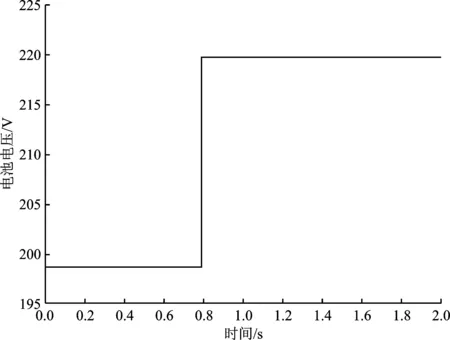
图14 蓄电池剩余容量为60%时蓄电池的端电压Figure 14. The terminal voltage of battery when the remaining capacity of the battery is 60%

图15 蓄电池剩余容量为90%时蓄电池的健康状态Figure 15. The state of health of the battery when the remaining capacity of the battery is 90%

图16 蓄电池剩余容量为90%时蓄电池的内阻Figure 16. The internal resistance of battery when the remaining capacity of the battery is 90%

图17 蓄电池剩余容量为90%时蓄电池的端电压Figure 17. The terminal voltage of battery when the remaining capacity of the battery is 90%

图18 蓄电池电流变化Figure 18. Battery current changes

图19 直流母线电压Figure 19. Voltage of direct current generatrix
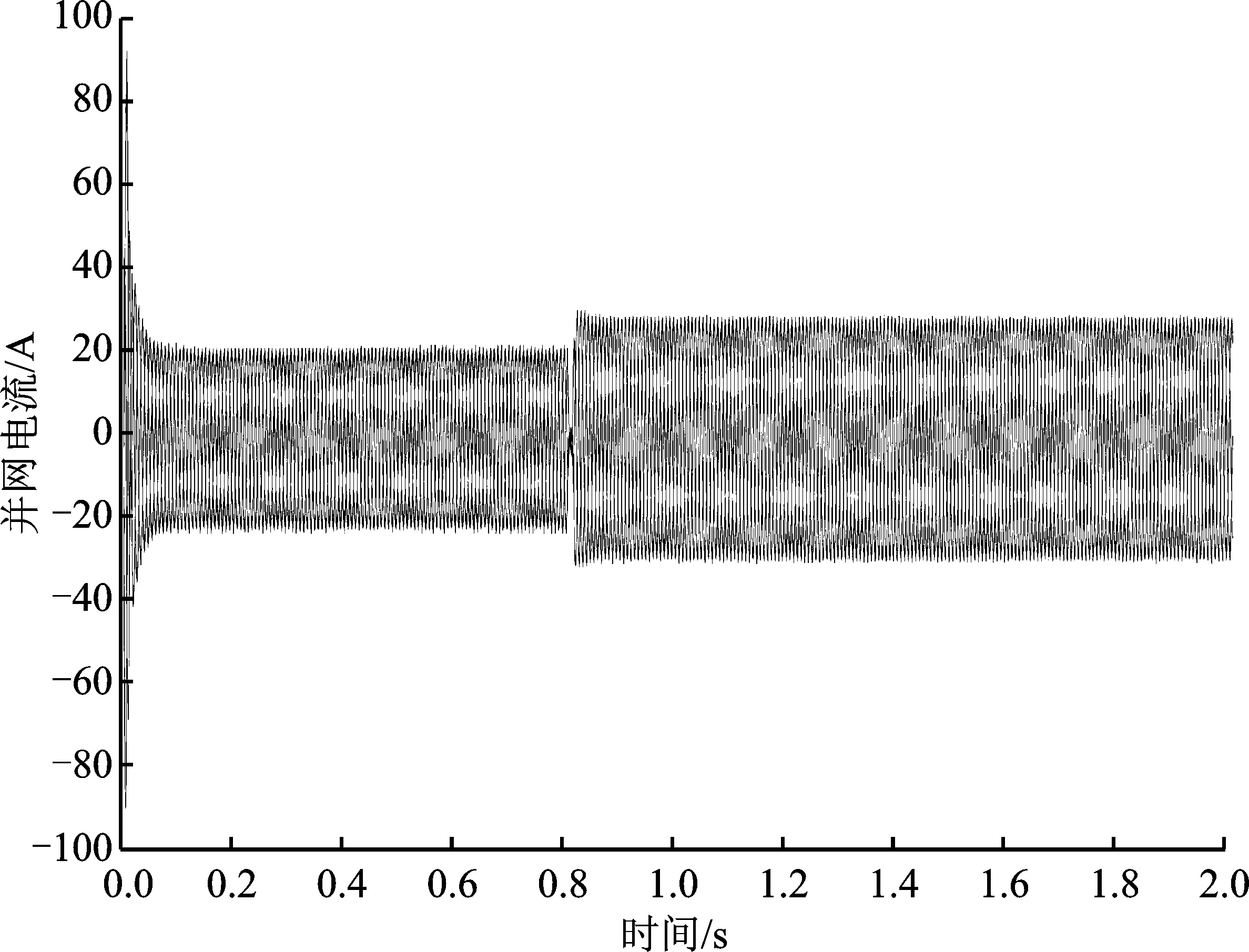
图20 并网电流Figure 20. Grid connected current
因蓄电池充放电流为给定值,故不受电池老化程度影响。本文采用恒电流的充放电模式,充放电流设定均为50 A。
3.4 稳压及并网运行分析
因电网电压和线路阻抗保持不变,故并网电流不受电池老化程度影响。此外直流母线电压可以稳定在700 V,标志着蓄电池并网成功。
4 结束语
本文以铅酸蓄电池三阶动态模型为背景,针对传统蓄电池以可变电阻箱进行性能测试所引起的系统动态响应欠佳的问题,从蓄电池化学反应原理及电气模型入手,搭建三阶动态数学模型,并给出电池内部具体参数取值情况,通过双向变换电路及逆变并网控制实现电池充放电。逆变电路采用电压电流双闭环控制,并通过空间矢量脉宽调制实现逆变器开关通断,经滤波后并入电网。在MATLAB/Simulink仿真平台搭建三阶蓄电池并网充放电仿真模型,仿真结果表明蓄电池各项性能参数动态响应良好,较传统检测方式操作方便、准确度高,直流母线电压可以稳定在给定值,并网电流符合系统并网要求。

