输电工程双平臂抱杆动力性能分析

李文斌，金 明，周 方，马 池，廖 赟，谢志勇，鞠彦忠，王德弘

(1.广东电网能源发展有限公司，广东 广州 510160；2.东北电力大学建筑工程学院，吉林 吉林 132012)

双平臂抱杆作为一种格构式高耸结构，其主要作用是依附在建输电塔，将输电塔塔材从地面转移到高空某特定位置处，是架空输电线路铁塔组立施工的主要提升工具[1-4].在重物起升、下降制动等过程中，由于外荷载变动较大，抱杆会受到较大的振动和冲击，其工作环境中又存在很多不同振型、不同频率的振动源，这些振动源的干扰在不同程度上会影响抱杆结构的安全可靠性和降低机械构件的寿命，甚至严重时可能会发生安全事故[5-6].

双平臂抱杆在力学性能上主要包括静态方面和动态方面，对于双平臂抱杆的研究，目前主要集中在静力方面，动力分析尚不多见[7-11].由于抱杆在实际工作过程中经常做起升、制动等复杂的机械运动，因此抱杆的动态方面是其一般的表现形式，而其静态则是抱杆在动态达到一个稳定不变状态时的特例.因此，能够准确地计算、描述实际工作情况下的抱杆各部分结构在外部激励作用影响下的动态响应，对双平臂抱杆的设计在实践和理论上提供了一定的借鉴作用.

在动力研究方面，国内外主要针对塔式起重机的动态性能做了相关探讨.Gao[12]在柔性多体动力学理论的基础上，针对回转制动时的塔式起重机，利用ADAMS有限元软件建立了柔性多体数值模型，对其进行了动力响应分析.滕儒民[13-16]等分别对塔式起重机的吊臂进行了模态分析和动态有限元研究.黄铭枫[17]、夏顺俊[18]进行了双平臂抱杆的高频天平测力试验，得到了抱杆结构在不同风向角条件下的体型系数.双平臂抱杆的结构形状和工作特点与塔式起重机有一定的区别，因此，研究双平臂抱杆的动态性能，特别是吊臂在不同吊点幅度处工作时，研究和分析双平臂抱杆的动态特性和动力响应，对其在工程上的应用提供了十分重要的参考依据，并可为双平臂抱杆优化设计提供计算依据和理论基础.

1 双平臂抱杆有限元模型的建立

1.1 T2T100双平臂抱杆的结构性能参数

(1)抱杆最大工作幅度为18 m；

(2)抱杆额定起升速度为25 m/min；

(3)抱杆工作状态下最大起重量为8 t；

(4)抱杆最大起重力矩为104 t·m；

(5)抱杆额定回转速度为0.35 m/min；

(6)抱杆吊臂两侧最大起重力矩差为40 t·m；

(7)抱杆最大工作幅度处额定起重量为5.07 t.

抱杆在施工时每侧吊臂使用7段吊臂节，共18 m幅度，吊臂为正三角形截面对称双平臂，拉杆两端采用Φ40钢丝绳，腰环采用Φ17.5钢丝绳以12道拉线布置方式进行布置.吊臂上、下弦杆均为方钢管，斜腹杆及水平腹杆均为圆钢管；标准节的主弦杆为方钢管，横杆和斜杆为角钢.抱杆所有钢材均采用Q345B，泊松比v=0.3，弹性模量E=2.06×1011Pa，密度ρ=7.85×103 kg/m3.

1.2 有限元模型的建立

根据抱杆实际工作情况，定义有限元分析时抱杆结构的材料及材料特性，采用Beam188单元(梁单元)模拟抱杆的杆身标准节、起重臂、杆顶等结构，将各杆件之间的连接方式设置为刚接；采用Link180单元模拟拉杆、内拉线、腰环拉线等柔性绳索结构，设置时选择仅能承受拉力.起重臂与回转体的连接处、杆身标准节与回转体的连接处均采取节点自由度耦合处理方式，释放吊臂转动轴(绕Y轴方向)转动的束缚.抱杆的边界条件为约束杆身底部4个节点及腰环打设点的所有自由度，即采用固定约束.利用ANSYS有限元软件建立的工作工况下的双平臂抱杆参数化数值模型.在有限元模型中，双平臂在水平面内的投影方向为X坐标方向，垂直于双平臂的方向为Y坐标方向，竖直方向为Z坐标方向.

2 双平臂抱杆的模态分析

由于双平臂抱杆属于多自由度体系，低阶自振频率对一个多自由度体系的动力响应贡献较大，因此，只需提取低阶自振频率就能很好的反应出双平臂抱杆的动力特性.

选取Block Lanczos法[19]进行有限元模态分析，提取了双平臂抱杆结构的前十阶自振频率及相应的振型，表1给出了双平臂抱杆的前十阶自振频率、自振周期及对应振型的振动特点.

双平臂抱杆的前十阶固有振型(实线表示抱杆变形后的形状，虚线表示抱杆变形前的形状)如图1所示.

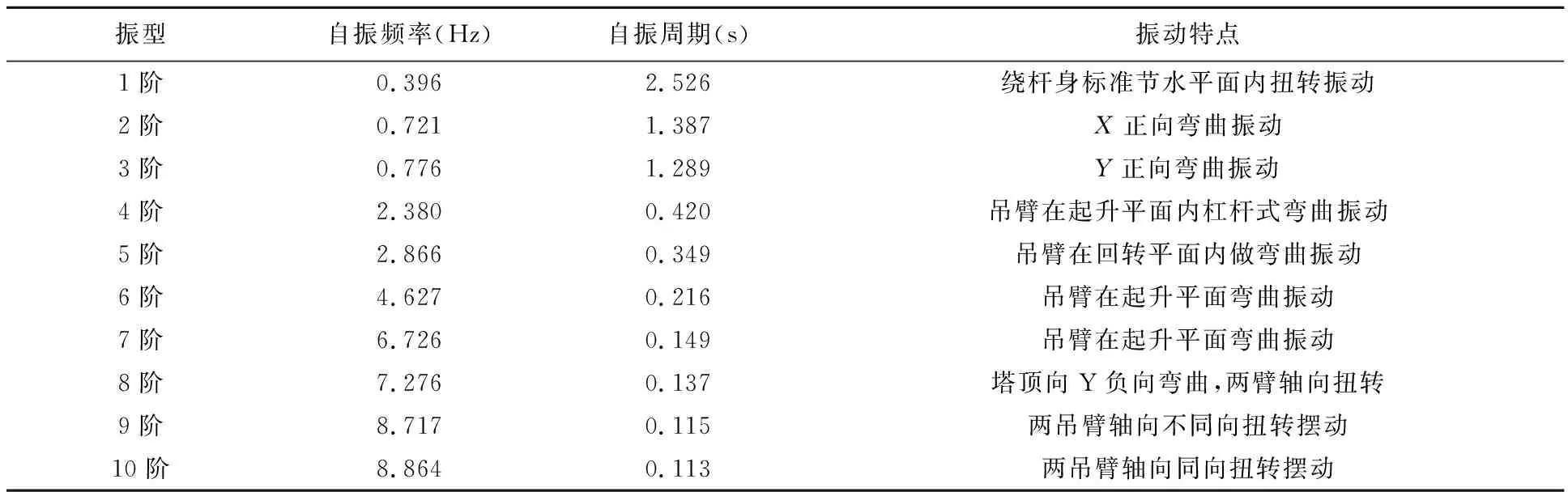
表1 前十阶自振频率、周期及振型特点

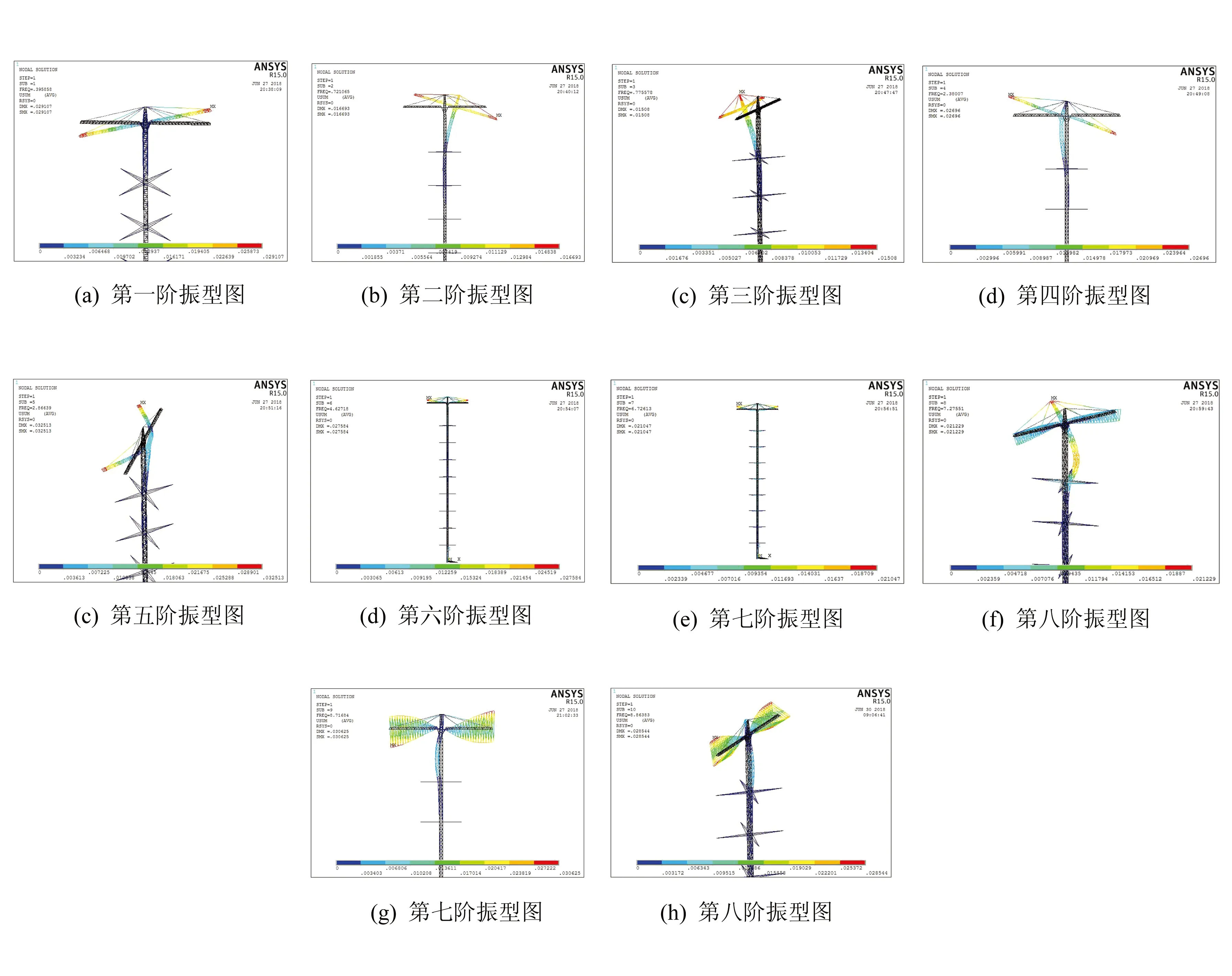
图1 抱杆前十阶振型图

3 双平臂抱杆的谐响应分析

为了获得结构在其自振频率处的位移响应，对双平臂抱杆进行谐响应分析.选取模态频率在0 Hz～10 Hz作为分析的计算范围[20].分别施加沿Z方向(抱杆的竖直方向)、X方向(双平臂方向)、Y方向(与平臂垂直的方向)的简谐激振荷载，针对双平臂抱杆有限元模型进行谐响应分析.

3.1 施加Z方向激励

在吊臂不同吊点处施加Z方向的简谐力，分别得到在9种不同起吊位置下平臂端部4049号节点和杆顶4944号节点发生最大位移时对应的自振频率.表2给出了9种吊点位置下4049号节点和4944号节点发生最大位移时对应的自振频率.

表2 抱杆发生最大位移时对应的固有频率

由计算结果可以看出，节点位移最大响应值均出现在第六阶自振频率处，当外部荷载为竖直方向时，抱杆的第六阶自振频率更容易导致结构发生共振，吊点位置在平臂16 m幅度处时Z方向位移响应峰值达到最大.

3.2 施加X方向激励

在抱杆所有节点处施加X方向的简谐力，得到4049号节点和4944号节点Z方向最大位移发生在第六阶固有频率(freq=4.627 Hz)处，X方向位移最大发生在第二阶固有频率(freq=0.721 Hz)处，X方向激励主要是风荷载的横向激励，当外部风荷载风振频率与结构第二阶固有频率相等时容易引起抱杆的共振.

3.3 施加Y方向激励

在抱杆所有节点处施加Y方向的简谐力，4049节点和4049节点Z方向最大位移发生在第六阶自振频率处，X方向最大位移发生在第三阶自振频率(freq=0.776 Hz)处，X方向激励主要是风荷载的横向激励，当外部风荷载风振频率与结构第三阶自振频率相等时容易引起双平臂抱杆的共振.

X方向和Y方向的激励荷载主要是风荷载产生的，如果双平臂抱杆的第2、3阶自振频率与风荷载的风振频率相等时，抱杆结构就会容易产生共振.Z方向的激励荷载主要是双平臂抱杆在实际工作中由起升机构对吊重物进行离地起升、下降卸载等作业时产生的动荷载，如果外界激励频率与双平臂抱杆的第六阶自振频率一致时，抱杆就会发生共振，此现象最为危险.

4 双平臂抱杆的动力响应分析

4.1 结构阻尼的选取

Rayleigh阻尼常被应用于结构的瞬态分析中，通常认为阻尼矩阵是由刚度矩阵[K]和质量矩阵[M]所组成的，因此可用数学表达式表示为

[C]=α[M]+β[K]

，

(1)

公式中：α为质量阻尼系数；β为刚度阻尼系数.

一般情况下α和β是由阻尼比ξ计算得来的，假设结构的第i阶自振频率为ωi，其阻尼比为ξi，则有如下关系：

(2)

分别取振型i和j，联立得：

(3)

求解方程组可得：

(4)

通常认为结构不同阶振型的阻尼比大小相等，取关键自振频率和，得到简化后的系数和系数分别为

(5)

公式中：ω1为结构一阶自振频率；ω2为结构二阶自振频率；ξ为结构阻尼比.

针对本文双平臂抱杆的动态分析，ξ选取=0.01，通过公式(5)可分别计算出质量阻尼系数α=0.032 12和刚度阻尼系数β=0.002 85.

4.2 载荷离地起升工况的动响应分析

双平臂抱杆施工时，首先需将吊重物从地面提升至一定高度，此工况称为离地起升工况.在吊装的过程中，抱杆结构受到的荷载是动荷载，与吊重物相连的钢丝绳产生的内力也是变化的.双平臂抱杆起吊塔材的过程可以分为三个时段[21]，如图2所示.

图2 抱杆离地起升过程

以双平臂抱杆起吊重物第二时段的开始时间t0作为时间0点，假设起升钢丝绳受到的拉力是线性增长的，可用图3表示抱杆整个起升工况的激振载荷变化情况.

图3 起升工况激振荷载变化曲线

选取双平臂抱杆9种起吊位置，当分别起升最大额定起重量时，计算得到抱杆在各吊点位置下起吊重物时的最大动应力，并将其与最大静应力对比得出起升动载系数，如表3所示.由计算结果可以看出，随着起重臂吊点幅度的增大，起重臂的动载系数增加较大，而杆身标准节的动载系数几乎不变.

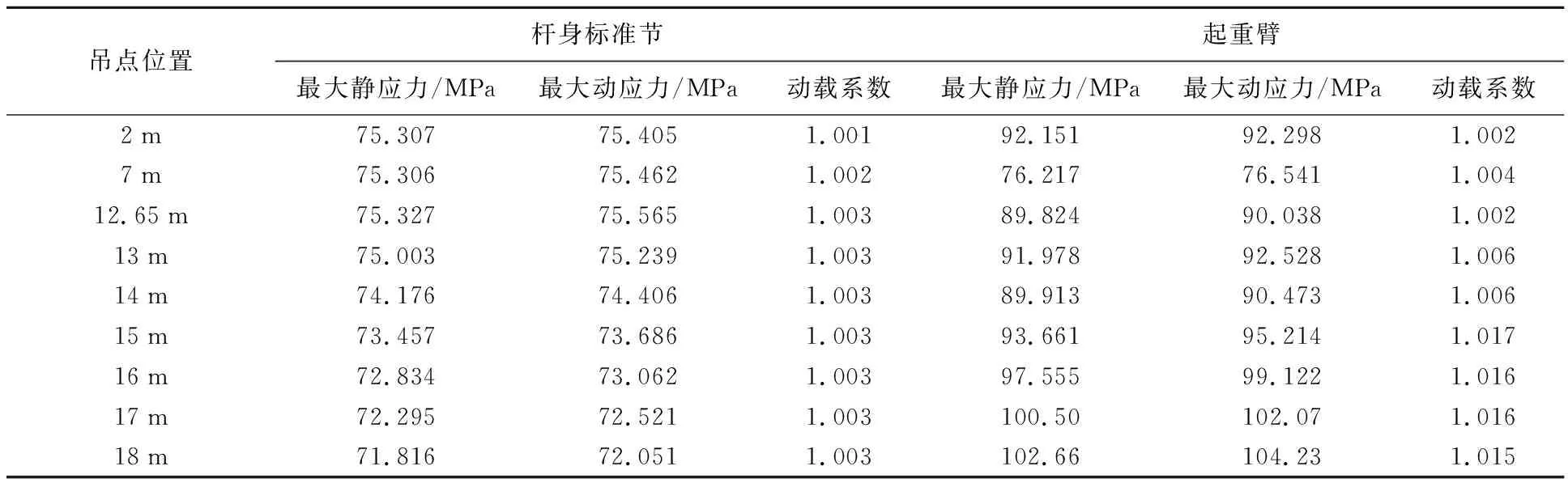
表3 载荷离地起升动载系数

选取双平臂抱杆18 m、16 m、12.65 m三种起吊位置，当分别起升最大额定起重量时，绘制得到双平臂抱杆的4049号节点(平臂端部节点)和4944号节点(杆顶节点)的位移响应曲线、起重臂和杆身标准节的最大应力响应曲线，如图4～图6.由图可以看出，双平臂抱杆在加载结束后发生振动，随着吊点幅度的增大，起重臂端部4049号节点Z方向位移响应也会增大，X方向、Y方向位移响应几乎无变化.由于阻尼的作用，节点位移、吊臂和杆身标准节最大应力呈现衰减趋势.

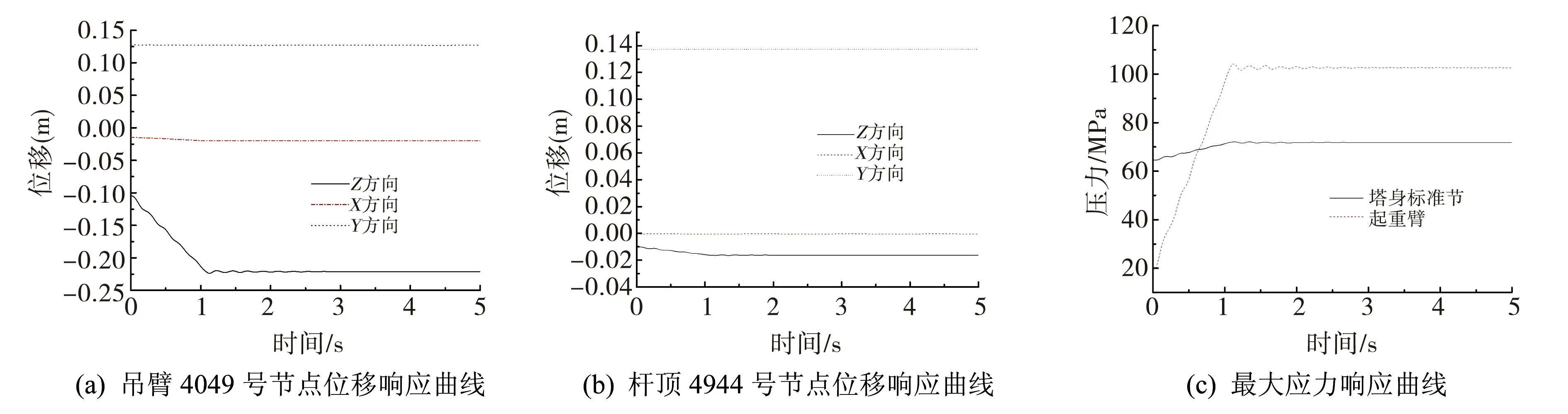
图4 18 m幅度起升额定起重量

图5 16 m幅度起升额定起重量

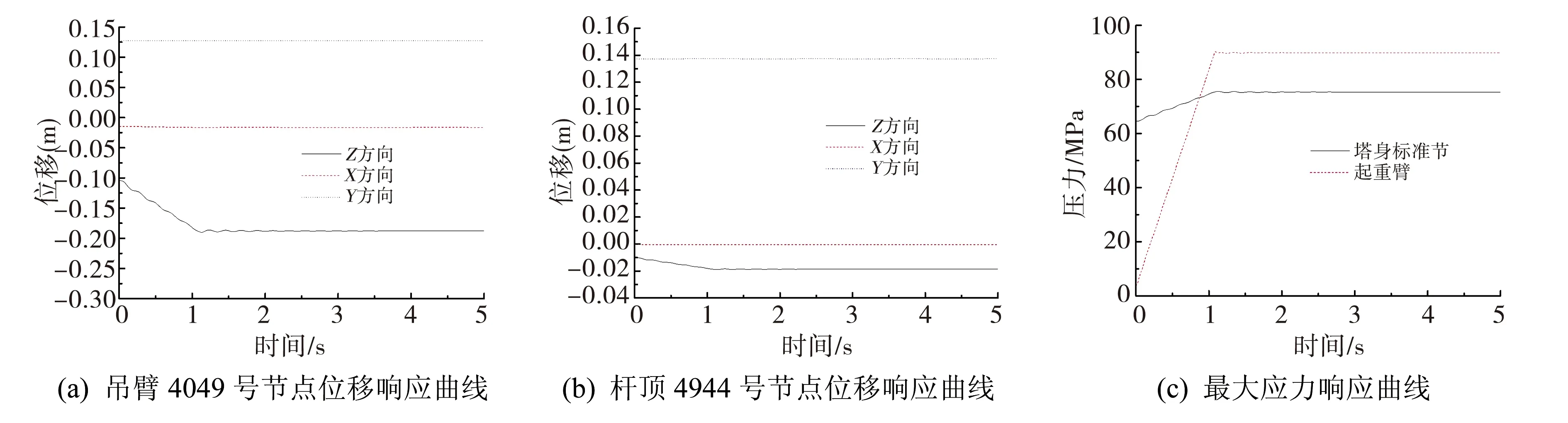
图6 12.65 m幅度起升额定起重量

4.3 降制动卸载工况的动响应分析

与离地起升的时段相反，双平臂抱杆在下降制动卸载时，以吊装的塔材与已建铁塔接触的瞬间作为时间0点，这时起升钢丝绳的拉力F仍与吊重物的重力mg相等；在起升机构的继续运转下，起升钢丝绳渐渐下降的同时其拉力也逐步减小，设当拉力减小至零时的时刻为t1，随后双平臂抱杆开始做自由振动，该过程的激振荷载变化曲线如图7所示.

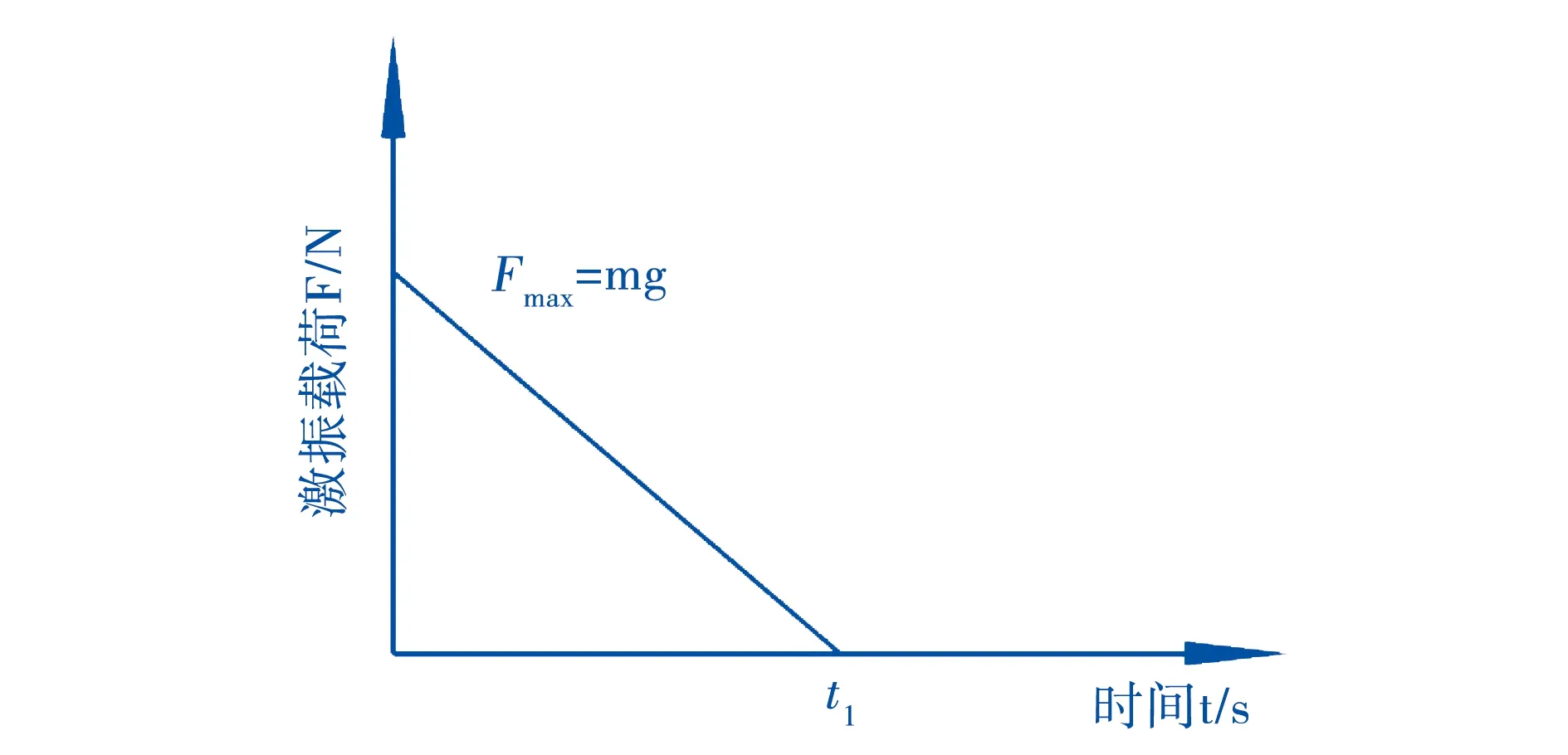
图7 下降制动工况激振荷载变化曲线

选取双平臂抱杆起吊位置为18m，当分别起升最大额定起重量时，绘制得到双平臂抱杆的4049号节点(起重臂端部节点)和4944号节点(杆顶节点)的位移响应曲线以及杆身标准节和吊臂的最大应力响应曲线，如图8所示.由图可以看出，双平臂抱杆在卸载结束后发生振动，随着吊点幅度的增大，起重臂端部4049号节点Z方向位移响应也会增大，而X方向、Y方向位移响应几乎无变化.由于阻尼的作用，节点位移、抱杆的起重臂和杆身标准节最大应力逐渐衰减.

图8 18 m幅度下降制动卸载

4.4 突然卸载工况的动响应分析

突然卸载是抱杆较为常见、也是抱杆结构受载最为不利的工况之一，选取双平臂抱杆起吊位置为18 m起吊位置，当分别起升最大额定起重量时，绘制得到双平臂抱杆4049号节点(起重臂端部节点)的位移响应曲线及起重臂和杆身标准节的最大应力响应曲线，如图9所示.由图9可以看出，当双平臂抱杆突然卸载时，起重臂端部节点的位移迅速减小，同时起重臂和杆身标准节的最大应力也迅速减小，其振幅相对于下降制动卸载工况要大得多，因此所受到的冲击荷载影响也会剧增，进入强烈振动状态.由于阻尼的作用，关键节点的位移、抱杆的起重臂和杆身标准节最大应力呈现衰减趋势.

图9 18 m幅度突然卸载

双平臂抱杆在起吊重物突然卸载时，冲击荷载会使抱杆产生强烈的振动，其影响程度用卸载冲击系数反应，该系数可通过卸载后峰值应力和卸载前静态应力比较得出.9种吊点位置下起升额定起重量突然卸载时的卸载冲击系数计算结果如表4所示.

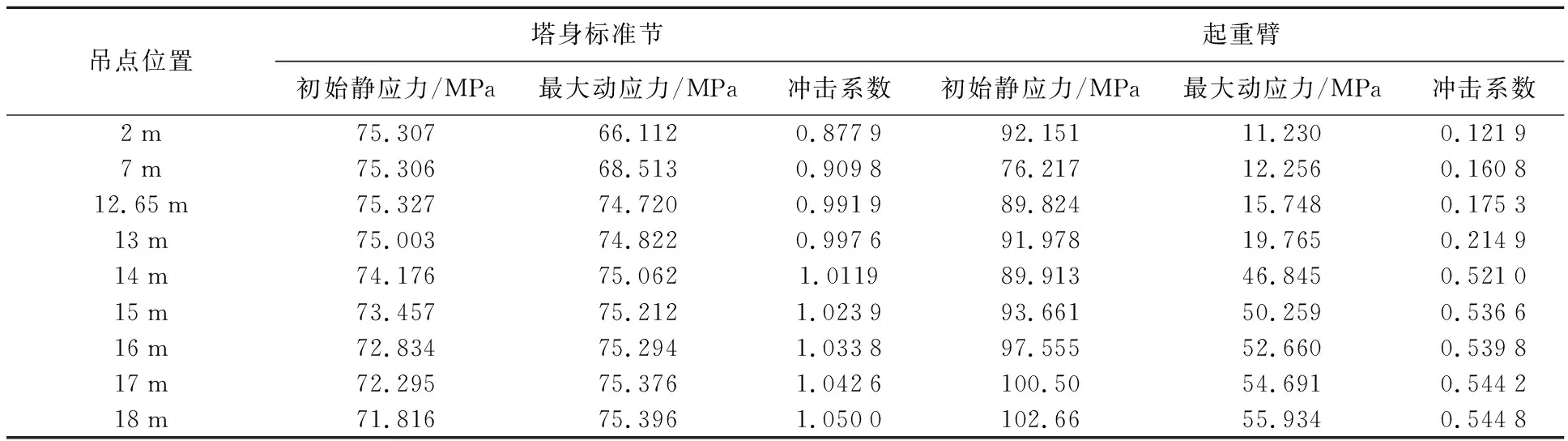
表4 载荷突然卸载冲击系数

由表4可以看出，突然卸载后抱杆结构产生强烈振动时，起重臂吊点幅度越大，塔身标准节和起重臂的卸载冲击系数也随之增大，其中，在小于等于12.65 m幅度时，起重臂的冲击系数相对较小，在大于12.65 m幅度时，起重臂冲击系数大幅提高，这表明吊点幅度对抱杆结构的卸载冲击系数影响较大，吊点幅度越大，在突然卸载工况下抱杆受到的冲击荷载影响也越大.因此，为保证施工安全，建议突然卸载工况标准节的冲击参数取1.1，起重臂的冲击参数取0.6.

5 结 论

本文利用有限元方法，对双平臂抱杆的动态特性和不同工况的动力响应进行了数值模拟，得到以下结论：

(1) 最大响应值均出现在第六阶自振频率处，在外部竖直荷载作用时，抱杆的第六阶自振频率更容易导致结构发生共振，吊点位置在平臂16 m幅度处时Z方向位移响应峰值达到最大.

(2)双平臂抱杆在起升载荷加载结束后发生振动，随着起重臂吊点幅度的增大，起重臂端部4049号节点Z方向位移响应随之增大，起重臂的动载系数增加较大，而杆身标准节的动载系数没有明显变化.抱杆在下降制动卸载工况下的动态响应与起升工况相反.

(3)抱杆在突然卸载后结构产生强烈振动，随着起重臂吊点幅度增大，抱杆受到的冲击影响也会随之增大，杆身标准节和起重臂的卸载冲击系数也随之增大，在实际施工作业中应避免吊重物突然掉落.为保证施工安全，建议突然卸载工况标准节的冲击系数取1.1，起重臂的冲击系数取0.6.