甘肃民勤风电塔筒结构的温度统计分析

孙玉萍,汪春林,李万润

(1.兰州理工大学土木工程学院,甘肃 兰州 730050; 2.兰州理工大学防震减灾研究所,甘肃 兰州 730050)

随着全球工业化和机械化的日益推进,能源短缺问题逐渐凸显,新能源的开发和利用成为各国关注的焦点。风能作为自然界中最常见的自然资源,应用也更加广泛,其主要应用于风力发电。当前,对于风电机组塔筒结构的研究主要侧重于结构的地震响应[1-2]、结构性能[3]、结构疲劳损伤分析[4-5]以及结构的动力特性分析[6-9]等。风电塔筒结构由于日照作用会产生变形、温度应力及附加应力,因此,温度效应是影响塔筒性能的重要因素之一。在风电塔筒结构设计阶段,为了分析结构的温度效应,需要掌握露天情况下塔筒结构的温度场分布以及随时间的变化情况。然而,相关的参考数据较为缺乏,规范中也没有明确的计算方法。

鉴于此,以甘肃民勤风电场风电塔筒为研究对象,通过监测系统对塔筒的温度场进行实时记录。根据实测温度数据统计结果,研究了风电塔筒的温度变化规律及塔筒与环境之间温差的分布特性,并建立了风电塔筒温度及温差的概率分布模型。研究成果可为深入研究风电塔筒的温度效应提供依据,并为我国风电塔筒的全寿命设计提供重要的基础数据和分析方法。

1 监测断面与测点布置

监测塔筒位于甘肃民勤风电场,为2.0 MW低温型电励磁直驱风电机组,测试塔筒为圆筒+圆锥形管状结构,由低合金结构钢Q345E组成,具有充足的刚强度,可以承担作用在叶片、塔筒上的力以及叶片转动引起的振动载荷。每段塔筒间通过法兰连接,具有很好的安全性。塔筒高度83 m,叶轮直径106 m,塔顶外径2.7 m,塔底外径4.0 m,额定风速10 m/s,额定转速15 r/min。为研究风电塔筒结构的温度分布特性,对风电场中的N18、N61、N70、N92及N108这5台风电机组进行了监测,在每个塔筒内壁及塔筒外部分别安装了2个温度传感器。风电机组塔筒结构及温度传感器测点布置示意图如图1所示。

图1 温度传感器测点布置Fig.1 Temperature sensor measuring point arrangement

2 数据预处理

选取监测塔筒2015年10月—2016年10月的温度实测数据进行分析。由于传感器自身的因素,监测到的数据可能存在异常,需要选择能够反映塔筒日温度变化的典型温度数据进行分析(将异常数据从分析数据中剔除),如图2所示。测试中温度传感器所使用的采样频率为0.1 Hz,由于采集的数据量比较大,且在短时段内温度变化不明显,以5 min为基本时距对采集到的温度数据取平均值,用平均值代表此时段的温度值。监测塔筒温度实测曲线如图3所示。由图3可以看出:塔筒温度夏季高冬季低,具有显著的季节特征;实测塔筒最高温度为46 ℃,最低温度为-24 ℃;实测环境最高温度为36 ℃,最低温度为-17 ℃;实测昼夜温差最大为25 ℃,月温差最大为38 ℃,年温差最大达到70 ℃以上。

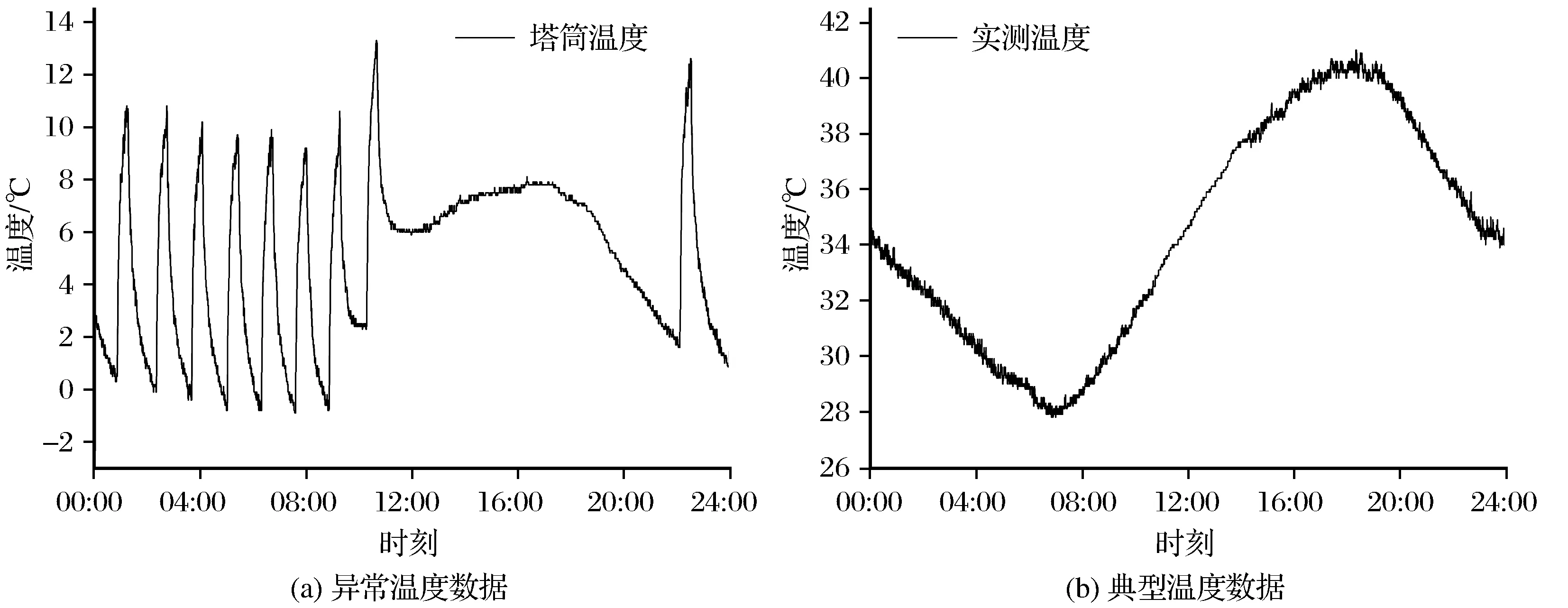
图2 塔筒温度实测数据的选取Fig.2 Temperature measurement data selection of wind turbine tower

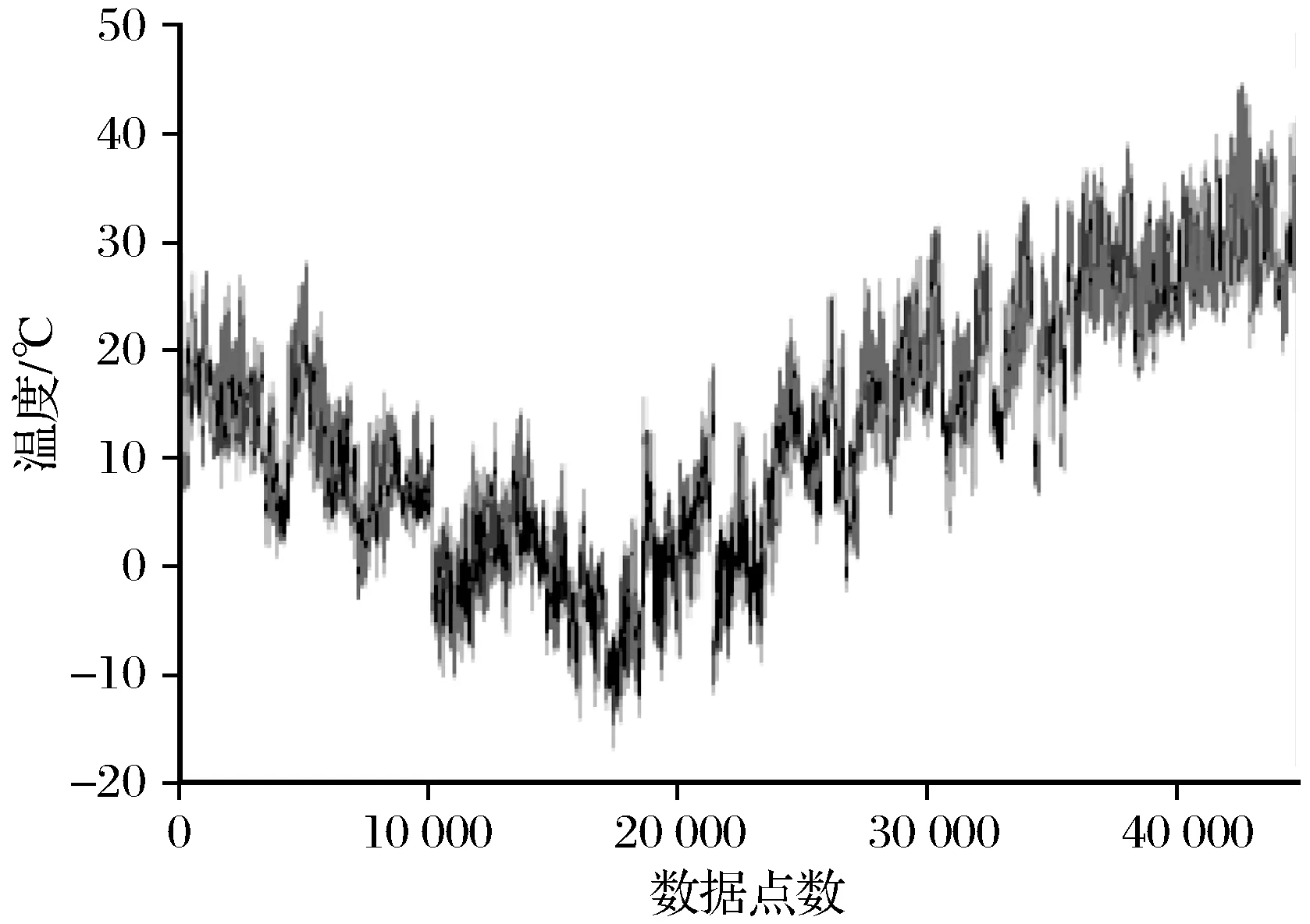
图3 塔筒温度实测曲线Fig.3 Temperature measured curve of wind turbine tower

2.1 温度统计分析

利用实测得到的数据对未知参数作最小二乘拟合,进而建立关于塔筒温度的概率密度统计分析模型。用Mi代替第i个月的温度数据,Qi代替第i个季度的温度数据,Y代替整年的实测温度数据。选取2015年12月温度样本TM12、春季温度样本TQ1及年温度样本TY,检验其是否服从统一分布。TM12与TQ1,TQ1与TY,TY与TM12的累加分布函数如图4所示。图4显示:TM12、TQ1与TY具有相同的累加分布函数。对监测塔筒的月温度、季温度及年温度样本在显著性水平为0.05条件下进行Kolmogarov-Smirnov检验,判定3个样本是否为同一分布。结果显示,TM12与TQ1,TQ1与TY,TY与TM12的检验结果均为0,接受服从同一分布假设。

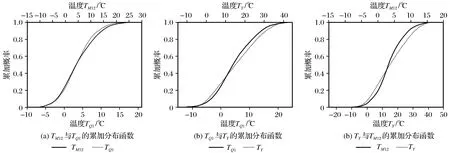
图4 监测塔筒温度样本的累加分布函数Fig.4 Cumulative distribution function of temperature samples of the measuring wind turbine tower

对监测塔筒的月温度、季温度及年温度样本进行统计分析,对检测数据采用各种概率分布模型做拟合优度比较发现,监测塔筒的月温度、季温度及年温度的概率统计特性均可以选用2个高斯分布的加权来表达,其概率密度表达式为

(1)

其中:fN(T,μi,σi)为变量为T、均值为μi、标准差为σi的正态分布函数;αi为第i个正态分布函数的权重;μi、σi和αi(i=1,2,…,n)为待估计参数,此处n=2。

塔筒月温度数据、季温度数据及年温度数据的概率密度柱状图及非线性回归曲线如图5所示。由图5可知,拟合曲线可以精确地描述塔筒温度的概率统计特性。对计算得到的温度概率密度曲线参数估计值进行K-S检验,结果均能通过显著性水平为0.05的K-S检验。

图5 塔筒月温度数据、季温度数据及年温度数据的概率密度柱状图及非线性回归曲线Fig.5 Histogram of probability density and nonlinear regression curve of monthly,quarterly, yearly temperature data of the wind turbine tower

2.2 温度标准值

我国《风力发电机组塔架》、《风力发电场设计技术规范》及《风力机设计通用要求》等规范对温度作用并没有相应的要求,温度标准值的确定参考了欧洲钢结构设计标准的规定,即

(2)

其中:f(T)为温差T的概率密度函数;N为实测数据数量;T为实际温度;T0为给定温差标准值;P为超越概率(T>T0的概率)。

将超越概率值P代入式(2),可以求出塔筒温度的标准值。利用估计的年温度概率密度函数可以解出温度作用标准值的最大值与最小值。通过求解得到其最大值为65.41 ℃,最小值为-30.03 ℃,温度作用标准值的最大值与最小值之差为95.44 ℃。塔筒结构材料为钢结构,温度对其作用明显,故在塔筒设计时需要考虑温度作用。

3 塔筒温差监测结果及分析

选取风场5台风电机组塔筒温度数据,计算塔筒温度与环境温度之间的温差,取其正温差样本进行分析。塔筒温度与环境温度正温差的实测曲线如图6所示。通过对各种拟合模型的比较,可用1个Weibull分布来表达塔筒正温差的概率统计,概率密度方程为

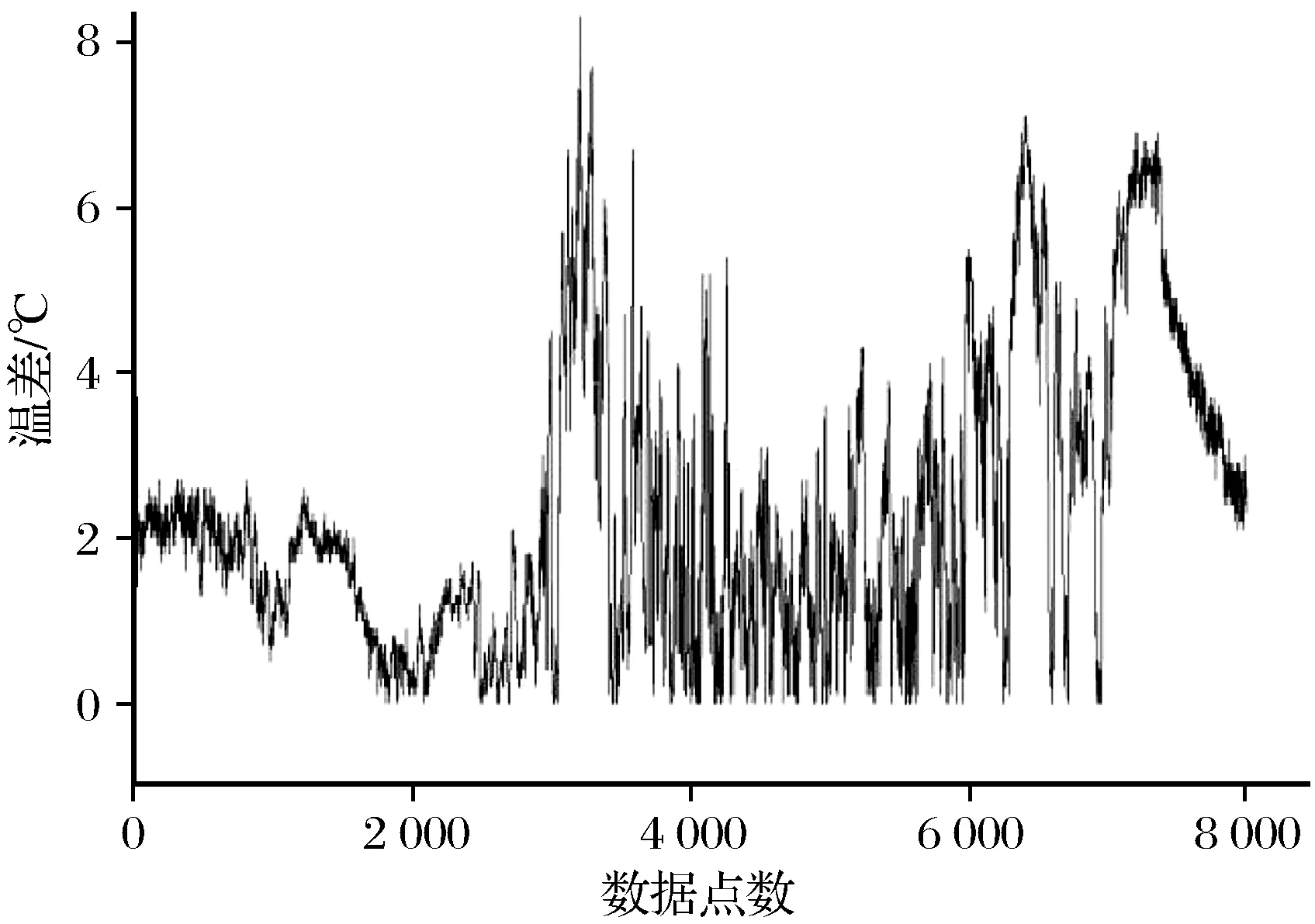
图6 塔筒温度与环境温度正温差的实测曲线Fig.6 The measured curve of the temperature difference between tower temperature and ambient temperature

(3)

其中:T为温差;α、β、μ为待估参数。

塔筒温度与环境温度正温差的概率密度柱状图、拟合曲线以及概率密度曲线参数估计值如图7所示。图7中拟合曲线可以精确地反映塔筒正温差的概率统计和参数α、β、μ的数值,并通过式(2)得到塔筒50年一遇的塔筒与环境温差的最大值为32.53 ℃。

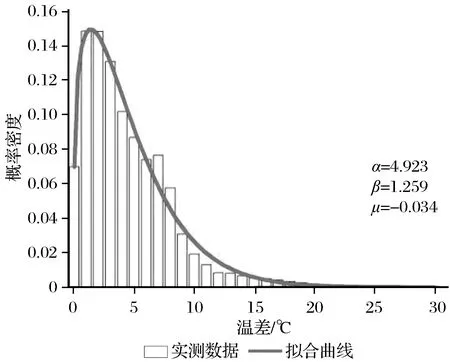
图7 塔筒温度与环境温度正温差的概率密度柱状图、拟合曲线及概率密度曲线参数α、β、μFig.7 Probability density histogram and fitted curve of positive temperature difference between tower temperature and ambient temperature,and the parametersα、β、μ of probability density

4 结论

基于民勤风电场风塔的温度长期在线监测数据,研究了塔筒结构的温度变化规律。利用数学统计分析法得到塔筒温度的变化特征,塔筒温度与环境温度之间的温差模型。

监测数据显示:风电塔筒温度存在明显的昼夜起伏现象;塔筒温度夏季高冬季低,具有显著的季节特征。风电塔筒的月温度、季温度以及年温度均可以通过2个正态分布函数的加权和来描述其概率分布。通过极值分析得到塔筒50年一遇的温度作用标准值的最大值为65.41 ℃,最小值为-30.03 ℃,年最大温差达到90 ℃以上。风电塔筒的塔筒温度与环境温度之间的正温差可以通过一个Weibull分布函数来描述其概率分布。通过极值分析得到塔筒50年一遇的塔筒与环境温差的正温差标准值的最大值为32.53 ℃。

研究结论只是针对甘肃民勤风电场的温度实测数据得出的,仅对其他不同太阳辐射地区的风电塔筒温度分布特征提供一个参考,具体还有待大量的现场实测和分析积累,这也是今后努力的方向。