材料电磁场计算模型合理性分析

王 雷,李旭东

(兰州理工大学省部共建有色金属先进加工与再利用国家重点实验室,甘肃 兰州 730050)

目前,电磁屏蔽性能的测试方法[1-3]有同轴测试法、双盒法、MIL-STD-285近场法[4]、屏蔽室法、波导管法;材料吸波性能的测试方法[5-8]有弓形法、同轴法、RCS测试法和时域测量法。传统的高频电磁场的研究方法[9-10]是通过特定的实验制作特定的结构材料,通过电磁性能测试方法,结合XRD、TEM、SEM等测试仪器,可以准确地测量材料的电磁性能、材料组成和体积电阻率。当然,这些方法也可以用来测量材料的电磁参数。

这样做往往需要以多种设计方案进行多次试制,不断总结经验,改进设计,这无疑增加工作量且成本过高,延长了产品设计和生产周期。同时,实验样品的可重复性较差,并且存在一定的盲目性。另一方面,传统的数值方法在理论上可以用来求解简单物体的解析解,但在求解复杂构件时却非常困难。随着国际竞争的激烈程度加剧,各国都在寻找更加经济的方法来降低实验成本,提高产品质量,缩短产品开发周期。因此很有必要对材料的电磁场效应进行计算机仿真研究[11-12]。

1 数值计算理论基础

1.1 电磁场有限元计算理论

电磁场计算以Maxwell方程组为基础,推导出Helmholtz方程,然后再求解出电场强度及磁场强度。电磁场强度是计算电磁场其他量的基础。

Helmholtz方程为

∇2ES=-k2ES。

(1)

式(1)在直角坐标系中会产生3个相量形式的标量方程(每个矢量分量都有一个对应的标量方程),且在每个方程中有4项。

Helmholtz方程的矩阵形式为

(2)

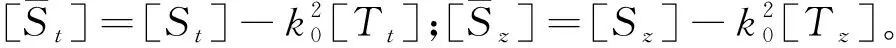
矩阵单元为

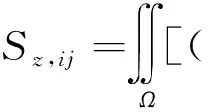
求解该矩阵方程,就可以求出电场强度的横向分量及纵向分量,从而求出电磁场度值。

1.2 透射率、反射率、吸收率计算原理

通过以传输线理论为基础的双端口算法,可以计算材料对平面入射电磁波的电磁响应程度,整个系统的入射功率、反射功率、透射功率示意图如图1所示,其中阴影区域为目标体。

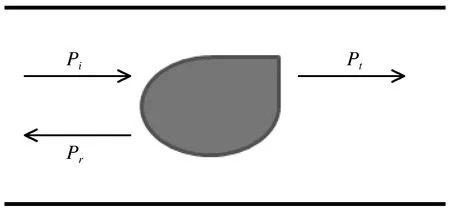
图1 系统的入射功率、反射功率、透射功率示意图Fig.1 Schematic diagram of the incident power,reflected power,and transmitted power of the system

目标体的反射率、透射率及吸收率的计算公式如下:

反射率的计算公式为

(3)

透射率的计算公式为

(4)

吸收率的计算公式为

(5)

其中:Pi为入射功率;Pr为反射功率;Pt为透射功率;Pa为吸收功率。

2 计算模型的建立

计算模型的整体几何模型如图2所示。

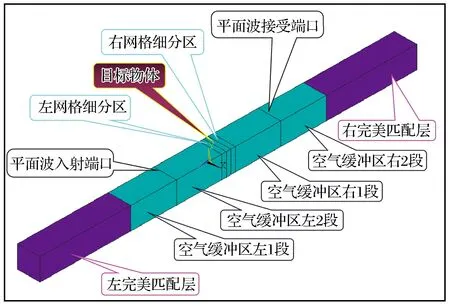
图2 计算模型的整体几何模型Fig.2 The overall geometric model diagram of the calculation model

模型尺寸:该模型入射电磁波的工作频率为10 GHz(即波长为30 mm),模型总长约为82 mm,约为波长的2.8倍。其中目标物体的厚度为1 μm,网格细分区的长度为1 mm,空气缓冲区的长度为20 mm,完美匹配层(PML,perfectly matched layer)的长度为20 mm。模型的宽、高均为5 mm。

材料主要参数:材料1:相对磁导率和相对介电常数都为1。材料2(目标物体):相对磁导率为1 000,电阻率为12 Ω·m,相对介电常数为100。

由于需要做大量的实验,若是通过图形用户界面操作,效率低且容易出错,因此采用ANSYS参数化设计语言(APDL,ANSYS parametric design language)编程实现ANSYS电磁场数值模拟几何模型创建、网格划分、边界条件加载、内部计算、数据输入与输出等全自动过程。图3为关键程序的截图,只需更改部分参数,就可以降低工作量。

3 结果分析

3.1 Z+轴空气缓冲区厚度分析

Z+轴空气缓冲区厚度为1 mm的模型和网格如图4所示。在不改变其他区域厚度和单元层数的前提下,将PML区和空气缓冲区的网格大小设置为1 000 μm,只改变Z+轴的空气缓冲区厚度,依次增加Z+轴的空气缓冲区厚度,每次增加空气缓冲区厚度为一层单元厚度,直到增加到20层单元厚度,查看Z+轴空气缓冲区厚度与电磁场效应之间的关系。

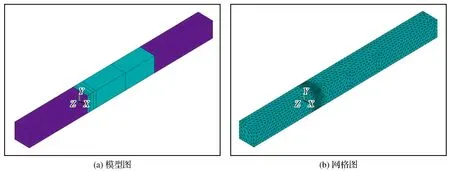
图4 Z+轴空气缓冲区厚度为1mm的模型和网格Fig.4 Model and mesh with air buffer thickness of 1mm on Z+ axis

Z+轴空气缓冲区厚度与电磁场效应的关系如图5所示。从图5中可以看出,反射率、透射率、吸收率之和并不等于100%,且误差较大。由于网格层数、模型长度都符合要求,这种误差是由于网格大小引起的,所以改变网格大小,再做一组实验。

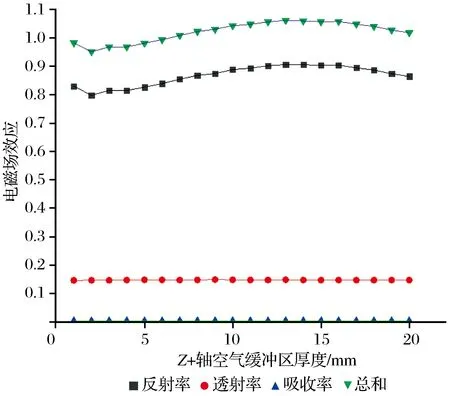
图5 Z+轴空气缓冲区厚度与电磁场效应关系Fig.5 The relationship between the thickness of the air buffer zone on the Z+ axis and the electromagnetic field effect

将实验条件设置为在不改变其他区域厚度的前提下,只改变PML区和空气缓冲区的网格大小,以原PML区和空气缓冲区的网格大小为参考,从原网格大小30%逐渐增加到2倍,查看PML区和空气缓冲区的网格大小对结果的影响。

不同网格大小的计算机实验结果数据如表1所列。表1显示,随着网格越来越大,反射率、透射率、吸收率之和越来越低,误差越来越大,这是由于网格细分区的网格大小为400 μm,所以选定原网格大小的40%,再做一组实验。

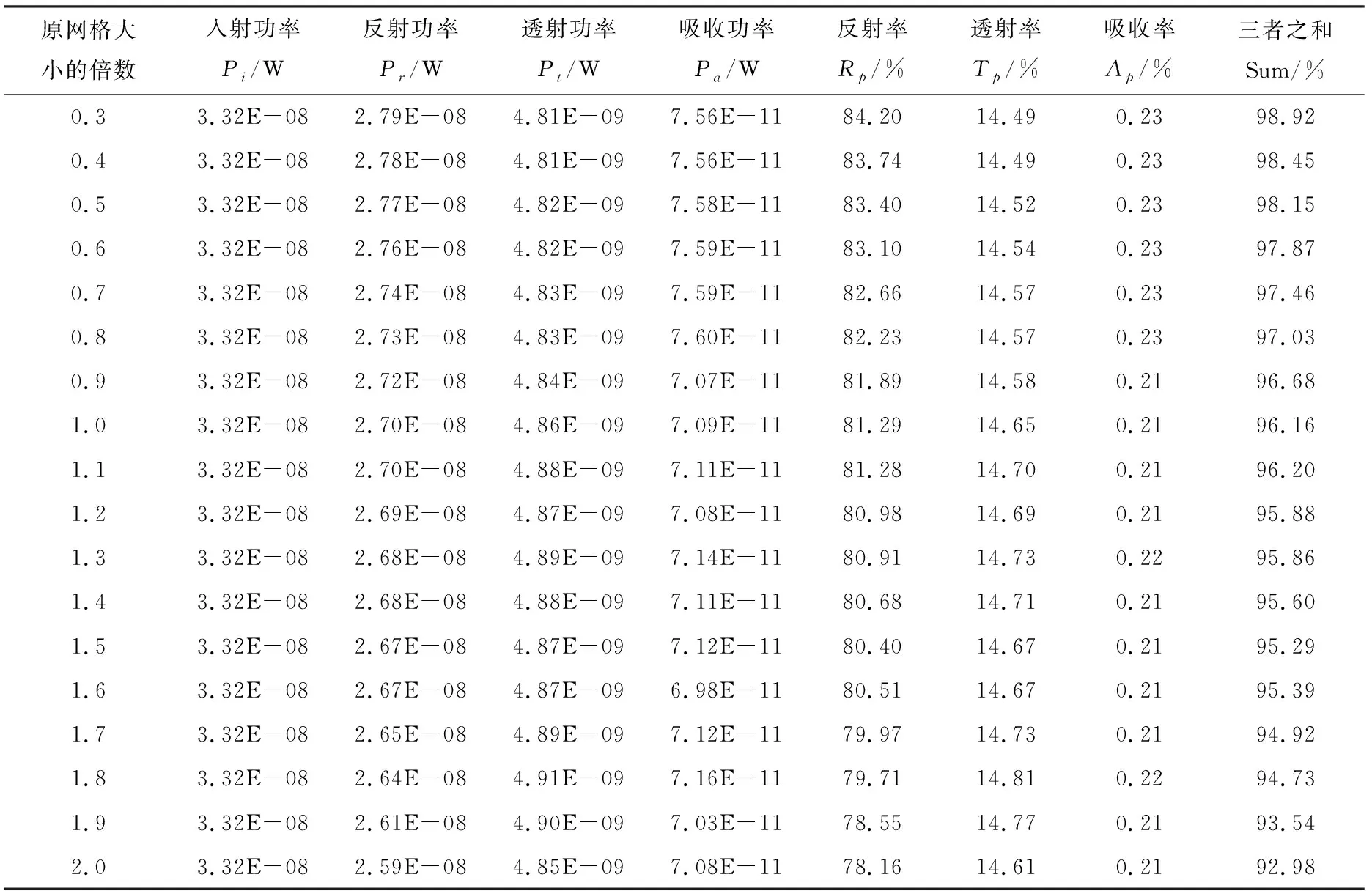
表1 不同网格大小的计算机实验结果数据Table 1 Computer experimental of result data of different mesh sizes

将实验条件设置为在不改变其他区域厚度的前提下,将PML区和空气缓冲区的网格大小设置为400 μm,只改变Z+轴的空气缓冲区厚度,依次增加Z+轴的空气缓冲区厚度,每次增加空气缓冲区厚度为1 mm,直到增加到20 mm,查看Z+轴空气缓冲区厚度对结果的影响。

网格优化后Z+轴空气缓冲区厚度的计算机实验结果数据如表2所列。表2显示,当空气缓冲区厚度只有1 mm和2 mm时,结果误差较大,反射率、透射率和吸收率之和分别为96.74%和97.89%。这是因为空气缓冲区的厚度较小，为0.5 mm,而空气缓冲区的网格尺寸较大，为0.4 mm,误差是在计算时网格迭代引起的。去掉这2个点,其余的反射率、透射率和吸收率变化都不大,可见Z+轴的空气缓冲区厚度对结果基本没有影响。由于细分区网格划分了3层,所以即使在最极端的情况下,也可以保证入射端口到目标物体有4层单元,这满足软件ANSYS电磁波传播模拟的最基本条件,所以整体曲线波动不大。

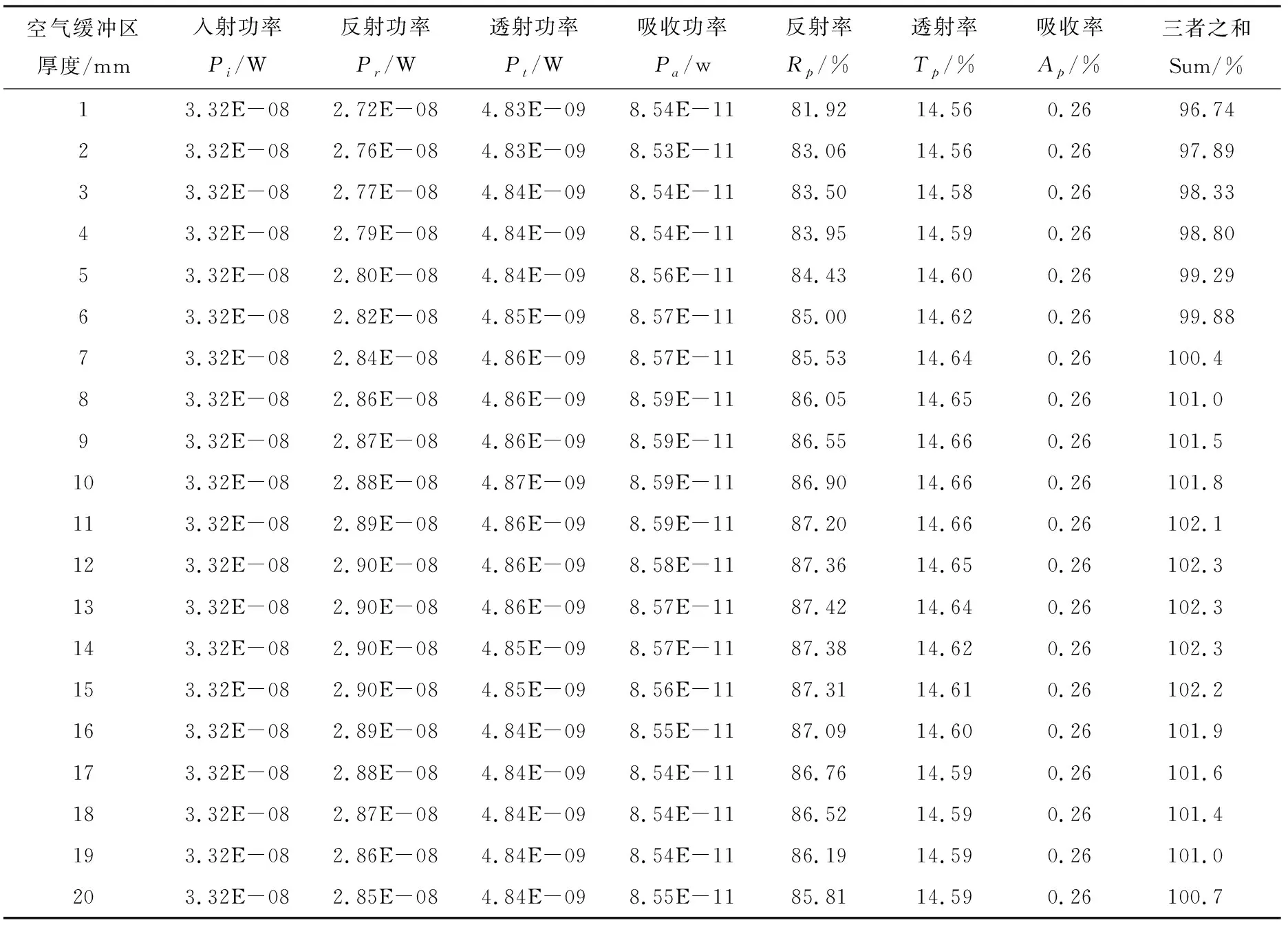
表2 网格优化后Z+轴空气缓冲区厚度的计算机实验结果数据Table 2 Computer experimental result data of air buffer thickness on Z+ axis after mesh optimization

3.2 Z-轴空气缓冲区厚度分析

Z-轴空气缓冲区厚度为1 mm的模型和网格如图6所示。在不改变其他区域厚度和单元层数的前提下,将PML区和空气缓冲区的网格大小设置为1 000 μm,只改变Z-轴的空气缓冲区厚度,依次增加Z-轴的空气缓冲区厚度,每次增加空气缓冲区厚度为一层单元,直到增加到20层单元厚度,查看Z-轴空气缓冲区厚度与电磁场效应之间的关系。

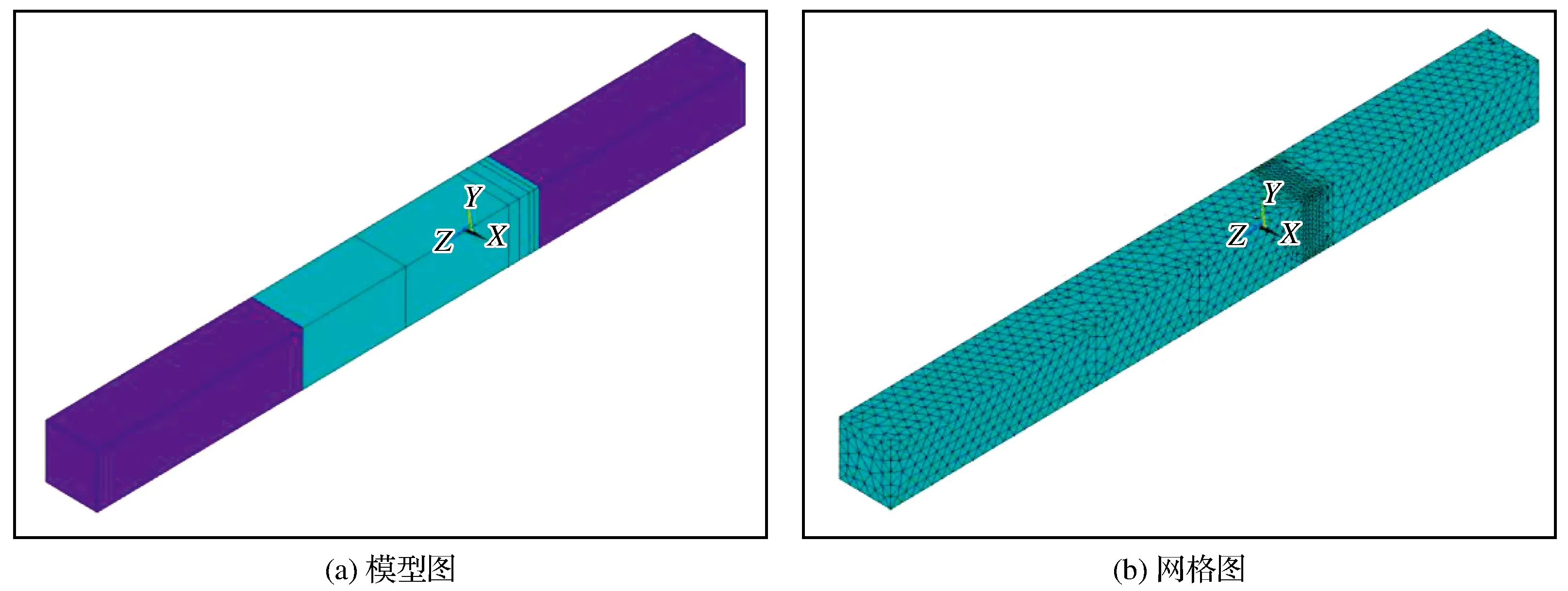
图6 Z-轴空气缓冲区厚度为1 mm的模型和网格Fig.6 Model and mesh with air buffer thickness of 1 mm on Z- axis

Z-轴空气缓冲区厚度与电磁场效应的关系如图7所示。从图7中可以看出,反射率、透射率和吸收率变化都不大,可见Z-轴空气缓冲区厚度对结果基本没有影响。这是因为细分区网格划分了3层,所以即使在最极端的情况下,也可以保证接受端口到目标物体有4层单元,这满足软件ANSYS电磁波传播模拟的最基本条件,所以整体曲线波动不大。

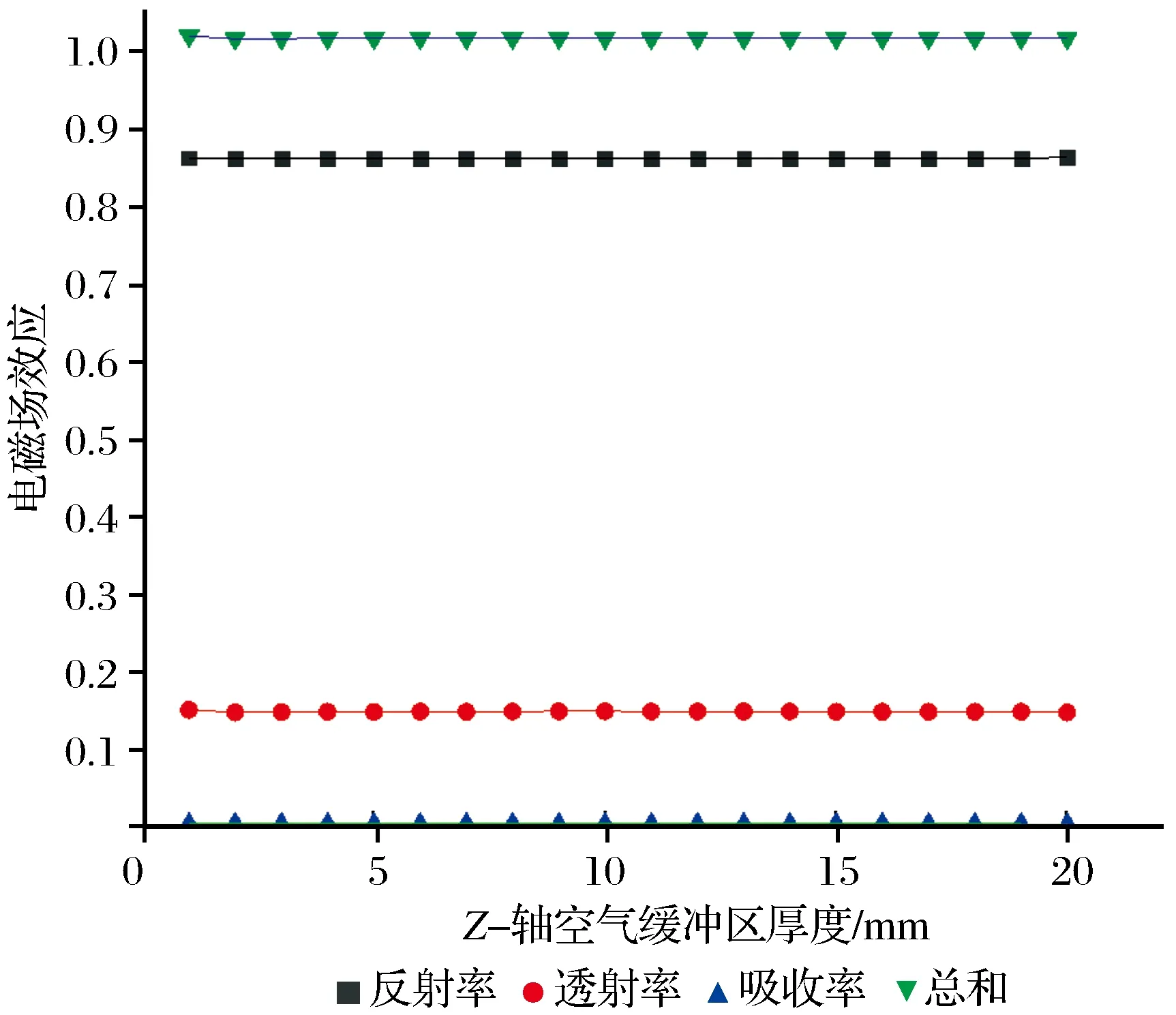
图7 Z-轴空气缓冲区厚度与电磁场效应关系Fig.7 The relationship between the thickness of the air buffer zone on the Z- axis and the electromagnetic field effect

3.3 Z+轴PML厚度分析

Z+轴PML厚度为1 mm的模型和网格如图8所示。在不改变其他区域厚度和单元层数的前提下,只改变Z+轴的PML厚度,依次增加Z+轴的PML厚度,每次增加PML厚度为一层单元,直到增加到20层单元厚度,查看Z+轴PML厚度与电磁场效应之间的关系。

Z+轴PML厚度与电磁场效应的关系如图9所示。从图9中可以看出,当Z+轴PML厚度小于4 mm时,结果是错误的。通过对应的模型网格图可知,此时的Z+轴PML不能划分出4层以上的单元,不能有效模拟材料对电磁波的远场吸收情况,所以结果是错误的,即Z+轴PML厚度至少应保证划分4层以上单元。

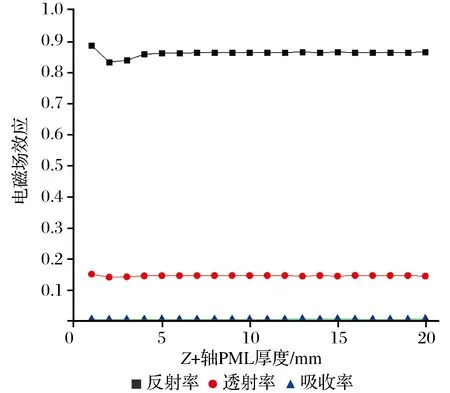
图9 Z+轴PML厚度与电磁场效应关系Fig.9 The relationship between the PML zone thickness of the Z+ axis and the electromagnetic field effect

3.4 Z-轴PML厚度分析

Z-轴PML厚度为1 mm的模型和网格如图10所示。在不改变其他区域厚度和单元层数的前提下,只改变Z-轴的PML厚度,依次增加Z-轴的PML厚度,每次增加PML厚度为一层单元,直到增加到20层单元厚度,查看Z-轴PML厚度与电磁场效应之间的关系。

Z-轴PML厚度与电磁场效应的关系如图11所示。从图11中可以看出,当Z-轴PML厚度小于4 mm时,结果是错误的,通过对应的模型网格图可知,此时的Z-轴PML不能划分出4层以上的单元,不能有效模拟材料对电磁波的远场吸收情况,所以结果是错误的，即Z-轴PML厚度至少应保证划分4层以上单元。

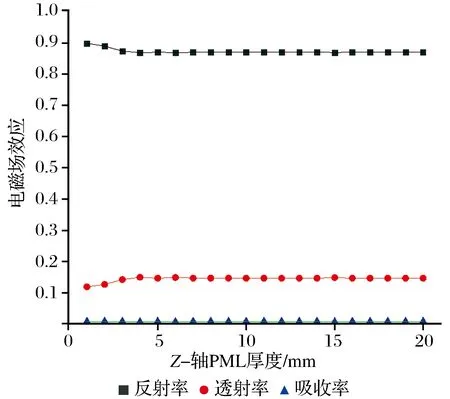
图11 Z-轴PML厚度与电磁场效应关系Fig.11 The relationship between the PML zone thickness of the Z- axis and the electromagnetic field effect

4 结论

基于电磁场有限元计算理论和反射率、透射率和吸收率的计算原理,采用双端口算法,利用APDL语言对ANSYS软件进行二次开发。通过Z+轴空气缓冲区厚度、Z-轴空气缓冲区厚度、Z+轴PML厚度、Z-轴PML厚度对计算模型的合理性进行了分析,最终确定了合理且通用的材料电磁场效应计算模型,主要结论如下:

(1) Z+轴空气缓冲区厚度的确定:Z+轴的空气缓冲区厚度对结果基本没有影响，但是其网格划分大小对结果有影响,合适的网格大小应该与网格细分区的大小相差不大。

(2) Z-轴空气缓冲区厚度的确定:Z-轴的空气缓冲区厚度对结果基本没有影响。

(3) Z+轴PML厚度的确定:Z+轴PML厚度应至少保证划分4层以上单元,取其为6层单元。

(4) Z-轴PML厚度的确定:Z-轴PML厚度应至少保证划分4层以上单元,取其与Z+轴PML对称,也为6层单元。