基于细观离散元方法的低渗透储层水力压裂数值模拟

李然，易新斌，王天一，卢海兵，姜馨淳，姜伟，王海，孙磊，尚大磊，王征

1 中国石油浙江油田分公司，杭州 310023

2 中国石油勘探开发研究院，北京 100083

3 中国石油集团渤海钻探工程有限公司，廊坊 065007

4 中国石油集团长城钻探工程有限公司压裂公司，盘锦 124000

0 引言

水力压裂是目前低渗透储层增产最常用的方法[1]，其实质是利用流体传压的特性，将压裂液注入储层产生水力裂缝。这个过程非常复杂，包含着渗流场与应力场的耦合作用。国内外学者对于低渗透储层压裂的研究取得了一系列成果，如Jacques、Brian等人[2]建立了水力压裂的裂缝扩展模型，认为注入率和孔隙驱替率对裂缝扩展有重要影响。Antońin、Michael等人[3]建立了拟三维水力压裂模型，认为储层与邻近隔层的应力差是控制垂直裂缝穿层的重要因素。Rahim、Holditch等人[4]引入三维概念建立了储层二维裂缝扩展模型。Zillur、Holditch等人[5]应用有限差分法分析了各种参数对储层压裂效果的影响。Wei、Economides等人[6]建立了水平井水力压裂裂缝扩展模型。国内学者程远方等人[7]从宏观角度讨论了水平井井眼方位、水平主应力与裂缝扩展的关系。张广清等人[8]建立了水平井筒附近水力裂缝空间转向模型，并利用室内实验验证所得结论。张广明等人[9-10]采用ABAQUS软件建立了储层水力压裂的三维数值模型。重要地，部分学者利用PFC颗粒流软件开展了水力压裂的数值模拟。颗粒流方法属于非连续介质力学细观离散元范畴[11-14]。该方法的核心思想是将模拟介质离散成一系列刚性颗粒，通过研究颗粒的运动来模拟实际材料的特定力学行为[15]。颗粒流方法模拟储层水力压裂过程无需设定裂缝界面单元[16-18]，因而得到的压裂裂缝更接近于实际裂缝形状，相较于连续介质力学模拟低渗透储层水力压裂更有优势。Al-Busaidi等人[19]基于PFC2D讨论了水力压裂起裂和扩展的力学机理。Shimizu等人[20]基于Cundall流固耦合算法，讨论了颗粒几何性质和压裂液性质对储层改造水力压裂断裂类型的影响机制。王涛等人[21-22]基于PFC建立了煤层气储层水力压裂数值模型，讨论了不同参数对起裂和扩展的影响规律。Yoon等人[23-24]基于Cundall流固耦合算法建立了水平井多簇压裂数值模型，讨论了缝尖应力干扰对多簇压裂的影响。周剑、张路青、韩正华等人[25-28]建立了基于Cundall流固耦合算法的数值模型，讨论了不同参数对水力压裂的影响规律。

虽然上述学者取得了一系列成果，但仍存在以下不足：(1)大多数学者仍采用宏观连续介质力学模型模拟储层水力压裂行为，这种方法需预先设定裂缝界面单元，即裂缝只能沿着设定的单元界面起裂和扩展。这与实际水力压裂过程中裂缝延伸方位存在一定差距，且此种情况下得到的裂缝形状偏于理想。(2)少数学者基于PFC颗粒流软件建立了水力压裂数值模型，从离散元角度讨论水力压裂力学机理。然而，上述数值模型均采用基于达西定律和泊肃叶方程的Cundall流固耦合算法，达西定律是基于实验结果拟合得到的经验方程，而泊肃叶方程并不适用于流速高的情况(水力压裂过程中压裂液流速较高)，这限制了水力压裂PFC流固耦合模型的计算精度。考虑到达西定律和泊肃叶方程均可以由物理意义非常明确、数学推导极其严谨的Navier-Stokes方程推导得到，笔者建立了基于N-S方程的水力压裂PFC-CFD流固耦合数值模型，并讨论了不同参数对水力压裂的影响。该方法对于拓宽低渗透储层水力压裂理论具有一定意义。

1 基于N-S方程的水力压裂PFC-CFD流固耦合数值模型

低渗透储层水力压裂是压裂液与储层耦合作用的复杂过程。在颗粒流耦合模型中，采用圆形颗粒模拟低渗透储层，通过运动方程描述颗粒运动，通过Navier-Stokes方程[29]描述压裂液运动，通过将压裂液的作用力作为外力施加给颗粒实现储层水力压裂的流固耦合作用。

1.1 Navier-Stokes方程

假设压裂液为密度不变的不可压缩流体，此时孔隙流体满足Navier-Stokes方程[29-30]：

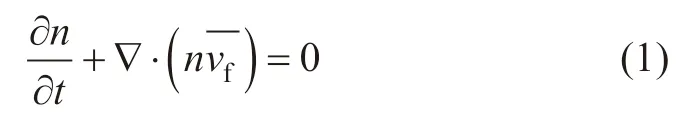
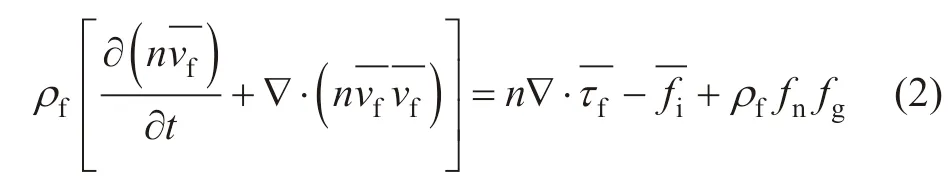
式 中，n为 孔 隙 率；t为 时 间，s；∇为 梯 度，为压裂液速度，m/s；ρf为压裂液密度，kg/m3；为平均应力张量；为压裂液对颗粒产生的拖曳力，N；fn为颗粒表面单位外矢量；fg为重力加速度，m/s2。

1.2 压裂液与储层颗粒相互作用分析

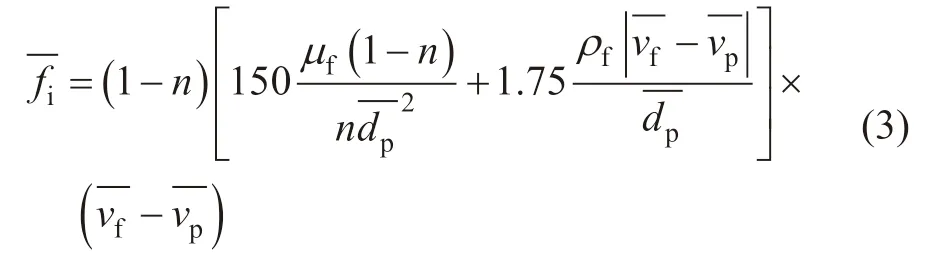
式中，μf为压裂液黏滞系数；为平均粒径，mm；为压裂液流速，m/s；为颗粒速度，m/s；Rep为雷诺系数，Cd为拖曳系数[31-32]。

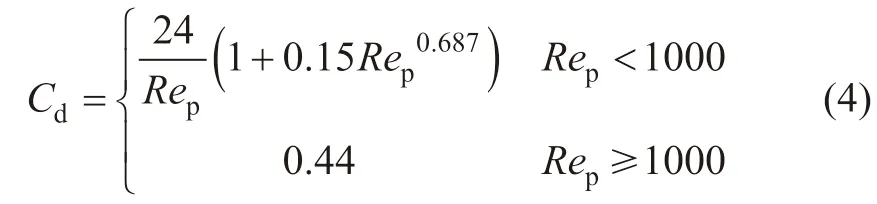
1.3 考虑压裂液作用的颗粒运动方程

储层颗粒在拖曳力作用下的运动满足牛顿第二定律[30,32-33]，见下式(5)～(6)：

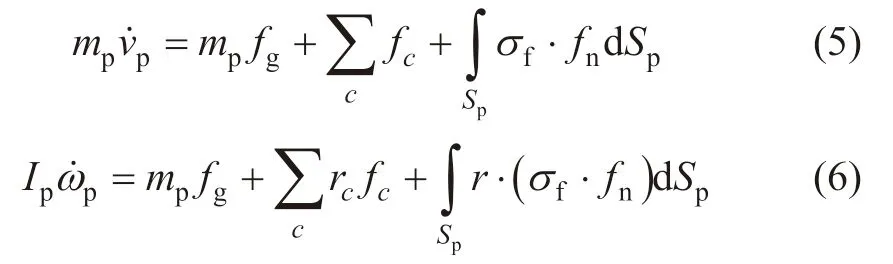
式中，mp为颗粒质量，g；νp为颗粒速度，m/s；Ip为颗粒转动惯量，g·mm；ωp为颗粒转动速度，rad/s；fc为颗粒间接触力，N；rc为方向矢量；r为半径矢量；Sp为颗粒表面积，mm2。

1.4 求解方法

由1.1～1.3节建立基于N-S方程的水力压裂PFCCFD流固耦合模型，求解方法见图1[34]。

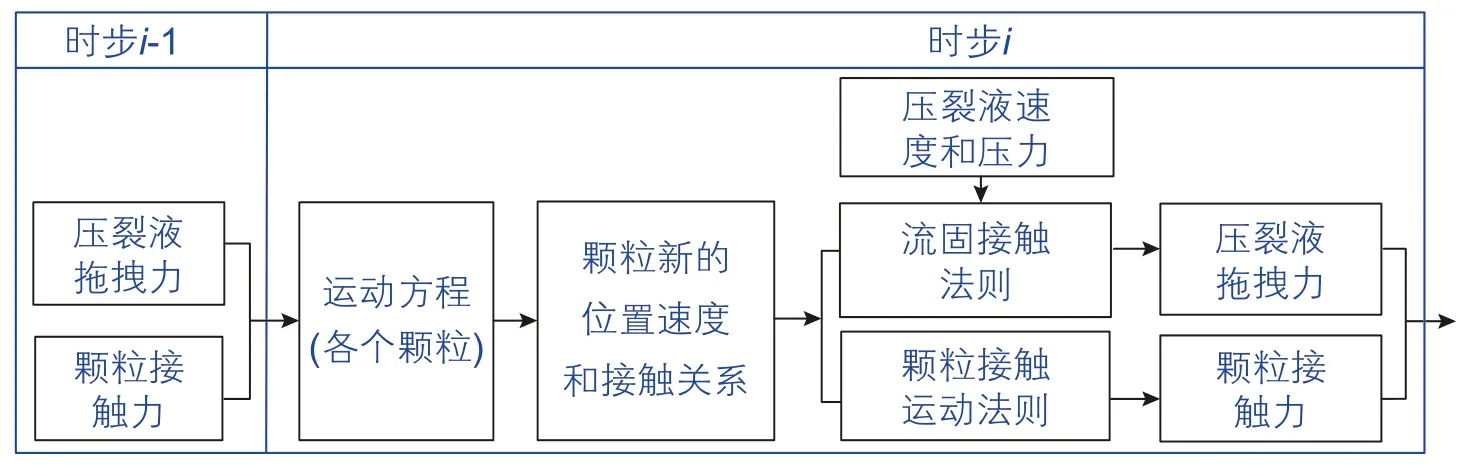
图1 水力压裂流固耦合模型求解过程Fig.1 Fluid-solid coupling model solution of hydraulic fracturing

2 基于接触平行连接模型的断裂失效模拟

采用颗粒流方法模拟低渗透储层的断裂行为时，需要在相邻颗粒间设定连接，通过判断平行连接失效形成微裂纹。平行连接在一个时间步长Δt内的弹性力及弹性力矩增量分别为[13-14,35]：

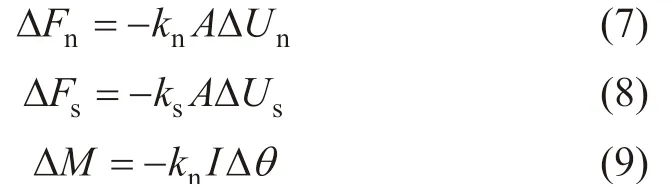
式中，A为接触连接面积，mm2；ΔUn、ΔUs分别为法向位移和切向位移，mm；Δθ为颗粒i和j的相对角速度；I为转动惯量，g·mm。

由式(7)～(9)，建立平行连接断裂的失效判据：

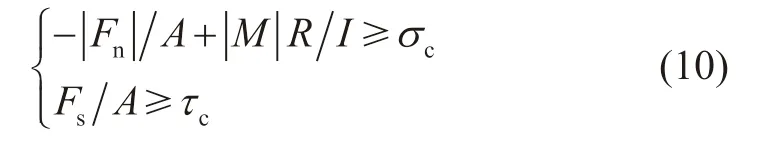
式中，Fn为法向力，N；Fs为法向力，N；M为力矩，N·m；σc、τc为抗拉、抗剪强度，MPa。

3 水力压裂颗粒流模型建立

3.1 储层水力压裂颗粒流模型

储层水力压裂离散元模型由墙体和圆形颗粒组成，生成后的模型如图2所示。图2中黄色圆代表待压裂储层颗粒，连接圆颗粒的绿色线段代表颗粒之间的接触连接；深蓝色圆点代表域，连接域的蓝色线段为压裂液注入储层后流动的缝隙通道。

图2 水力压裂的颗粒流数值模型Fig. 2 Particle flow numerical model of hydraulic fracturing

3.2 颗粒流数值模型参数确定

借助PFC中的双轴数值试验，通过反复对比数值试验结果与实际结果，确定本次模拟所用的颗粒流细观力学参数，见下表1。

表1中细观力学参数所对应的宏观力学参数数值试验结果为：弹性模量33.7 GPa，泊松比0.28，抗压强度117 MPa，抗拉强度9.2 MPa；与实际地层的宏观力学参数接近，其中弹性模量35 GPa，泊松比0.26，抗压强度120 MPa，抗拉强度10 MPa。数值试验结果与实际结果对比可知，表1中给出的细观力学参数可以满足计算要求。对应于储层颗粒基本参数，流体域基本参数如下表2所示。

表1 储层颗粒细观力学参数Table 1 Reservoir particles micromechanics parameters

表2 流体域基本参数Table 2 The basic parameters of the fluid domain

3.3 模拟过程

采用PFC软件模拟以下因素对储层压裂行为(如起裂压力、缝长、缝宽等)的影响。

(1) 储层颗粒细观力学参数一定的条件下，不同注入压力对压裂效果的影响。其中，注入压力变化范围：10～50 MPa，每次增加5 MPa。

(2) 在最优注入压力下，最大、最小水平主应力对压裂效果的影响。其中，初始最大主应力为25 MPa，最小主应力为20 MPa；每次增加0.5 MPa。

(3) 在最优注入压力下，颗粒法向接触刚度(kn)与切向接触刚度(ks)对压裂效果的影响，其变化范围为：2～10 GPa，每次增加0.5 GPa。

(4) 在最优注入压力下，颗粒法向连接强度σc与切向连接强度τc对压裂效果的影响，其变化范围为：10～30 MPa，每次增加2 MPa。

4 模拟结果分析

4.1 注入压力对储层压裂的影响分析

下图3为不同注入压力条件下微裂缝数目随时间子步的变化关系。

由图3可知，当注入压力P0＜28.9 MPa时，储层未出现微裂纹，表明颗粒间平行连接的拉应力和剪应力均小于平行连接抗拉强度和抗剪强度，此时储层微裂缝数目为0。当注入压力增大到28.9 MPa时，平行连接承受的拉应力及剪应力超过颗粒连接强度，颗粒间平行连接断裂产生裂缝，这时的注入压力即起裂压力。当注入压力P0在区间28.9～40 MPa时，微裂缝数目随时间缓慢增加，并在某一时间子步后趋于一稳定值，此时多条短裂缝相互贯通形成一条主裂缝；当注入压力P0＞40 MPa时，裂缝数目会在非常短的时间内达到非常高的数值。此时井眼附近除存在主裂缝外，还在其他方向存在多条压裂裂缝，引起井眼失稳。

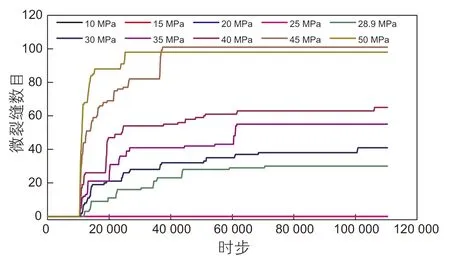
图3 不同注入压力下微裂缝条数随时间子步的变化关系Fig. 3 The number of micro-cracks with the time variation of the sub-step for the injection pressure

从图4中可以看出，储层最大缝长、缝宽随注入压力的增大先增加后减小，其原因为注入压力的增大使得主裂缝周围出现多条与主裂缝近似垂直的短裂缝，抑制了主裂缝沿长度方向的扩展。整体来看，缝宽与缝长变化规律基本相似，但缝宽在注入压力超过42.5 MPa后再次增大。这主要是因为随着注入压力增大，井眼周围地层聚集的能量增大，在裂缝沿长度方向扩展受到限制后，裂缝宽度将增大，这是由功能原理决定的。根据计算结果可知，P0=35 MPa为本次模拟的最优注入压力。下图5为最优注入压力下的水力压裂裂缝扩展几何形态。

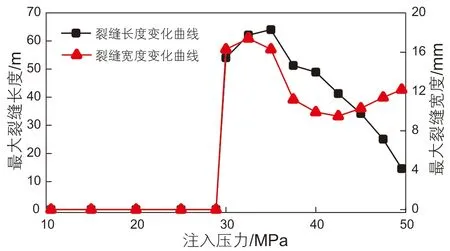
图4 最大裂缝长度及宽度随注入压力的变化关系Fig. 4 The relation between fracture length and width and injection pressure

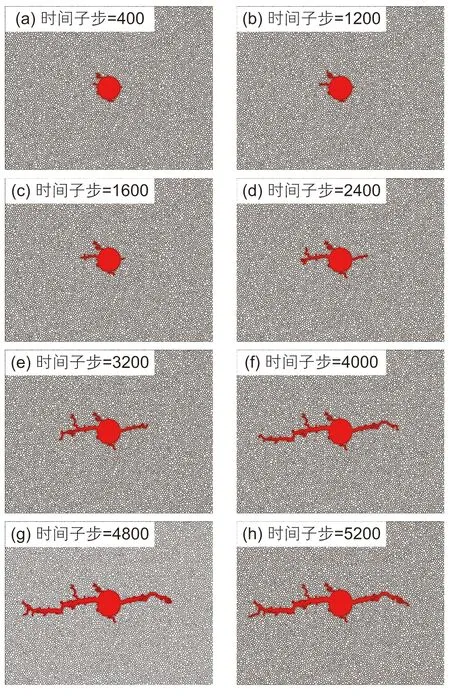
图5 最优注入压力下不同时间子步的裂缝扩展几何形态Fig. 5 The fracture propagation shape of different time substep for the optimal injection pressure

4.2 水平主应力对储层压裂的影响分析

改变最大、最小水平主应力σH、σh，讨论主应力变化对起裂压力、最大缝长及缝宽的影响，如图6～7。

由图6～7可知，随着最大水平主应力的增大，起裂压力及裂缝最大长度和宽度几乎不变，表明最大水平主应力对裂缝扩展影响甚微。相反地，最小水平主应力对起裂压力、最大缝长、缝宽的影响非常明显，起裂压力随着最小水平主应力的增大而线性增加。另外，最大缝长和最大缝宽随最小水平主应力的增大而减小。

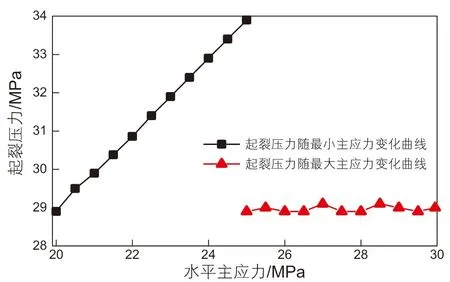
图6 起裂压力随水平主应力变化的关系曲线Fig. 6 The relation between initiation pressure and horizontal principal stress

4.3 法向与切向接触刚度对储层压裂的影响分析

改变颗粒法向与切向接触刚度kn、ks，讨论接触刚度变化对起裂压力、最大缝长及缝宽的影响，如图8～9。

由图8～9可知，颗粒切向接触刚度对起裂压力、最大缝长与缝宽的影响较小，而法向接触刚度对储层压裂效果的影响较为明显。起裂压力与颗粒法向接触刚度的关系近似呈线性；随着颗粒法向接触刚度的增大，最大缝长与缝宽大致呈线性减小趋势。

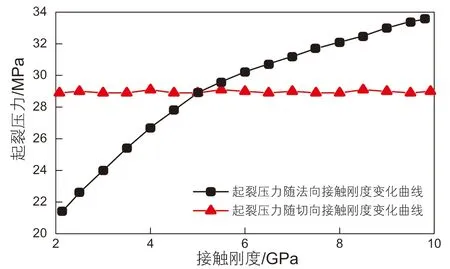
图8 起裂压力随颗粒接触刚度变化的关系曲线Fig. 8 The relation between initiation pressure and particle contact stiffness

4.4 法向与切向连接强度对储层压裂的影响分析

分别改变颗粒法向与切向连接强度σc、τc，讨论连接强度对起裂压力、最大缝长及缝宽的影响，如图10～11。

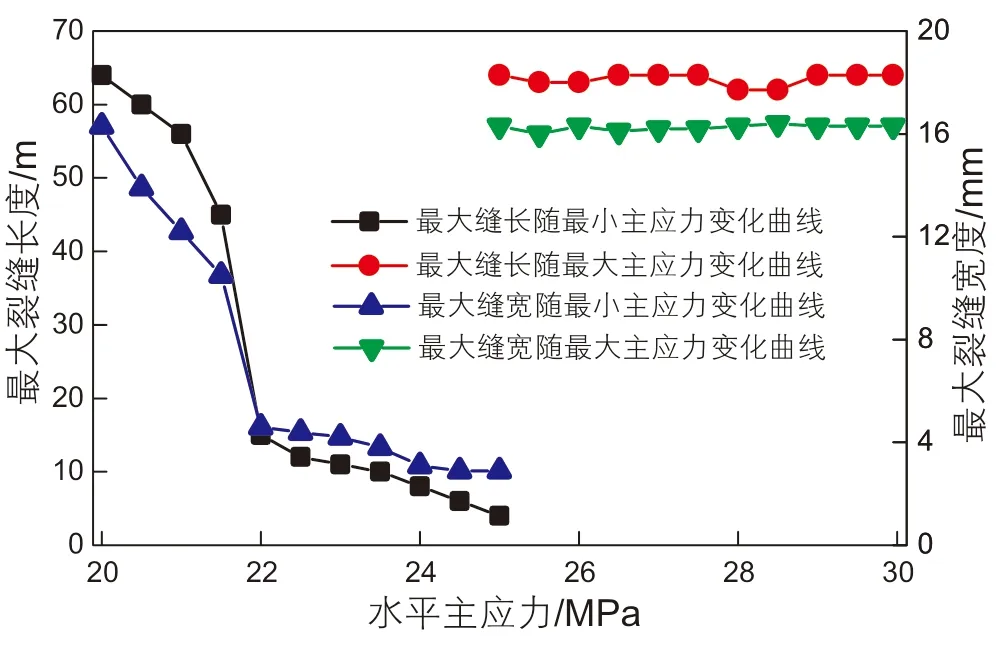
图7 最大缝长、缝宽随水平主应力变化的关系曲线Fig. 7 The relation between fracture length and width and horizontal principal stress

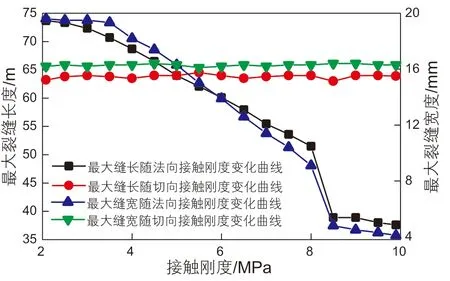
图9 最大缝长、缝宽随颗粒接触刚度变化的关系曲线Fig. 9 The relation between fracture length and width and particle contact stiffness

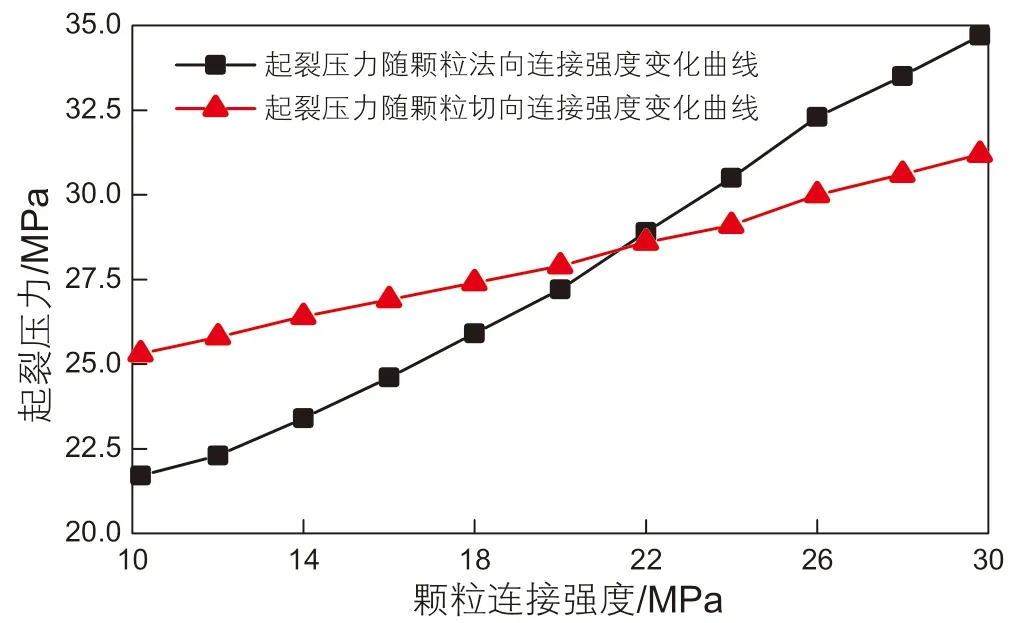
图10 起裂压力随颗粒连接强度变化的关系曲线Fig. 10 Th e relation between initiation pressure and particle connection strength

由图10可知，随着法向连接强度、切向连接强度的增大，储层起裂压力明显增加，且法向连接强度对起裂压力的影响大于切向连接强度。由图11可知，随着法向、切向连接强度的增大，最大缝长、缝宽近似呈二次抛物线关系减小。

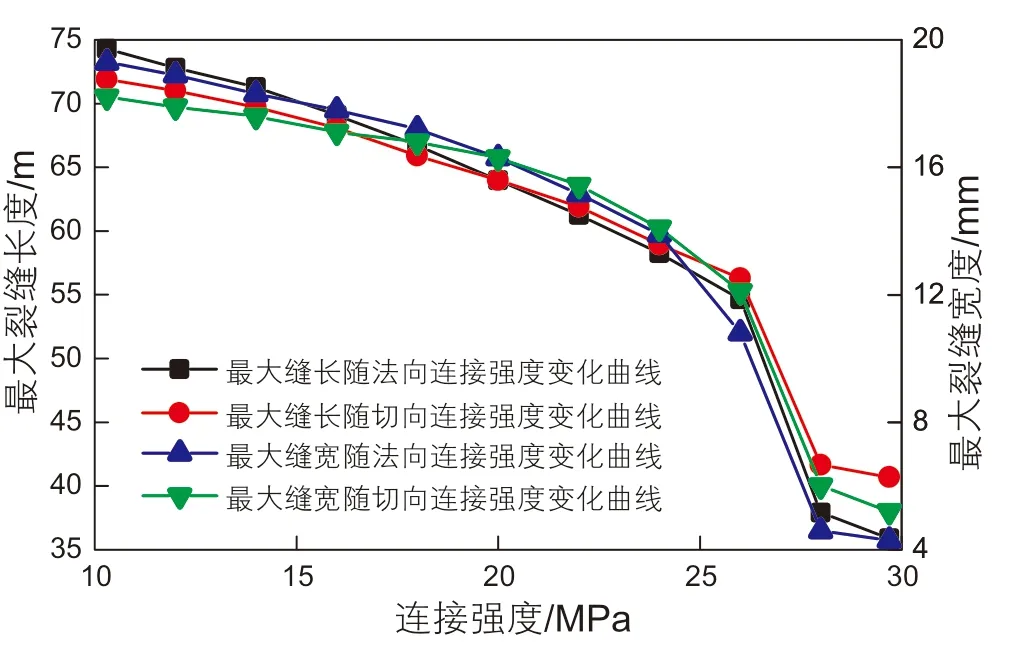
图11 最大缝长、缝宽随颗粒连接强度变化的关系曲线Fig. 11 The relation between fracture length and width and particle connection strength

5 结论

(1) 建立了基于N-S方程的低渗透储层水力压裂PFC-CFD流固耦合数值模型，并讨论了注入压力、水平主应力、颗粒接触刚度、颗粒连接强度等参数对低渗透储层压裂行为的影响。

(2) 分析了基于颗粒间平行连接模型的储层微裂纹形成机制，获取了任一时间步长内的弹性力及弹性力矩增量表达式。在此基础上，给出了颗粒间平行连接断裂的张拉失效和剪切失效判据公式。

(3) 随着最小水平主应力、颗粒法向接触刚度、颗粒法向及切向连接强度的增大，起裂压力近似呈线性增加而最大缝长、最大缝宽呈减小趋势。最大水平主应力、颗粒切向接触刚度对起裂压力、缝长、缝宽的影响甚微。