基于最优传播路径的EMA/EKF定位算法研究

盛孟刚，娄 兴，陈洋卓，张带凤，龚巧婷

(湘潭大学自动化与电子信息学院，湖南 湘潭 411105)

0 引言

在实际生活中，人们对定位服务不再仅满足于室外定位，对于室内定位的需求也日益增长，因此室内定位技术也越来越受重视。蓝牙定位技术功耗低，定位所需基站数量较少，使其定位成本低廉，且定位精度高，更适用于室内定位。目前，蓝牙室内定位主要采用接收信号强度指示(Received Signal Str-ength Indicator，RSSI)[1]和到达角(Angle-of-Arri-val，AOA)[2]进行定位，随着蓝牙5.1协议的颁布，基于AOA定位方法使蓝牙定位系统精度从米级提高到分米级。

蓝牙AOA定位研究通常从基站布设和定位算法性能提升两方面进行分析。其中，在基站布设方面，采用AOA算法进行定位至少需要2个基站才能完成行人定位，而基站的分布会对定位精度产生影响，现已有部分学者对此问题进行了研究。文献[3]研究了基站分布对于定位精度的影响，对视距(Line-of-Sight，LOS)环境中基站的分布进行研究，该研究所提出的Y型基站分布模型信号覆盖率达88.6%，但该系统适用于室外定位，且定位所需基站较多，定位成本较高；文献[4]对天线阵列排列进行研究，通过消除基站天线阵列分布造成的误差从而提高定位精度，该方法二维定位精度为1.45m。在定位算法方面，文献[5]提出了一种使用硬件设备提高AOA精度的方法，该方法测试误差达0.19°，但定位所使用的硬件设备成本较高；文献[6]提出了一种用于低功耗蓝牙定位的高精度AOA估计算法，该算法考虑载波频率偏移(Carrier Frequency Offset，CFO)，AOA平均测量误差为5°，但该方法并未考虑非视距(Non-Line-of-Sight，NLOS)影响；文献[7]对基于相位差的AOA定位算法进行研究，AOA平均测试误差达1.9°，该方法有效提高了AOA测试精度，但只针对LOS情况下进行研究，并考虑NLOS对测试精度的影响；文献[2]为提高测量角度的准确性，采用卡尔曼滤波器和高斯滤波器对原始I/Q采样信息进行处理，减少由NLOS造成的多径、噪声等影响，通过非线性最小二乘算法进行拟合，最终得到角度测量误差小于1°；文献[8]为消除无线信道对接收信号的影响，引入最小二乘算法、零迫等化器和快速傅里叶变换对I/Q采样信息进行处理，测量角度误差小于1°；文献[9]对角度测量值进行加权，增加了测量值准确度，平均定位误差低于0.23m，但定位过程中有出现位置跳变的情况；文献[10]使用MUSIC算法对角度测量值进行处理，融合定位误差小于2m。以上研究主要针对信号解析带来的误差，并未考虑NLOS范围与基站位置分布的关系对于定位精度的影响。

本文对基站安装位置与基站接收信号范围的关系进行研究，通过改变基站安装位置增加蓝牙信号视距接收范围。在此基础上提出了适用于室内环境下的蓝牙定位方法，通过基于蓝牙AOA的定位算法，提出了改进的指数移动平均(Exponential Moving Average，EMA)算法结合扩展卡尔曼滤波(Extended Kalman Filter，EKF)算法对室内行人进行定位。

1 基于遗传算法的最优基站几何分布

在有较多障碍物的定位场景中，如图1所示，考虑障碍物对蓝牙信号造成的遮挡，使蓝牙信号到达接收点前存在折射和反射等情况，出现信号多径传播，影响接收端接收信号的质量，使目标位置解算存在较大偏差。

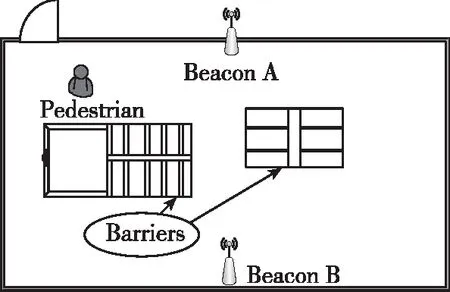
(a)室内基站安装俯视图

1.1 蓝牙基站布设位置与NLOS范围关系

使用天线阵列进行蓝牙信号接收，由文献[11]可知，蓝牙基站天线阵列接收范围存在30°较差区域，如图2(a)中角β所示，当待测目标处于该区域内时，无法对角度进行准确测量。当由于基站布设不合理导致室内部分区域处于该接收范围之内时，会影响蓝牙定位精度。若为提高定位精度加设定位基站，会导致定位成本增加。

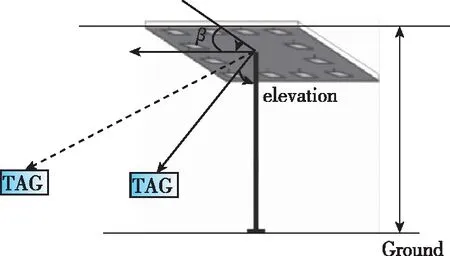
(a)基站天线示意图

当室内存在较少障碍物时，部分区域会受到弱NLOS影响，如图3所示。

图3 室内信号接收范围图Fig.3 Receiving range of indoor signal

根据图2(b)所示几何关系，则基站信号接收范围存在如下关系

(1)

其中，D为信号接收范围半径；H为基站安装高度。图2(b)中β=30°，则

C=H/sin(β)

(2)

即C=2H。

则式(1)可表示为

(3)

考虑单个障碍物对于基站接收信号范围的遮挡影响，如图4和图5所示，则NLOS区域范围大小与基站安装位置存在如下关系

(4)

其中，H为基站布设高度；h为障碍物高度；lx=|X-xi|为障碍物与基站间水平距离，xi为障碍物的X轴坐标；Jx为由障碍物产生的NLOS范围大小，对式(4)进行等式变换，则

(5)

图4 俯视图Fig.4 Top view

图5 障碍物造成NLOS范围大小Fig.5 Non-line-of-sight range caused by obstacles

假设室内存在N(N≥2)个障碍物，则由基站布设位置可得

(6)

即应使由基站布设产生的NLOS信号接收范围S为

(7)

其中，Jxi(i=1,2,…,N)为在二维区域中，第i个障碍物的遮挡产生的NLOS范围的高；bi(i=1,2,…,N)为第i个障碍物的长度。

同理可以推出Y轴方向上的障碍物所产生的NLOS范围大小为

(8)

其中，Jyi(i=1,2,…,N)为在二维区域中，第i个障碍物的遮挡产生的NLOS范围的高;ai(i=1,2,…,N)为第i个障碍物的宽度。

由以式(7)、式(8)可以得到室内环境下的NLOS范围的目标函数为

(9)

1.2 基于遗传算法的最优基站位置

有很多的优化方法可以对目标函数式(9)进行求解，本文选用遗传算法(Genetic Algorithm，GA)进行求解。

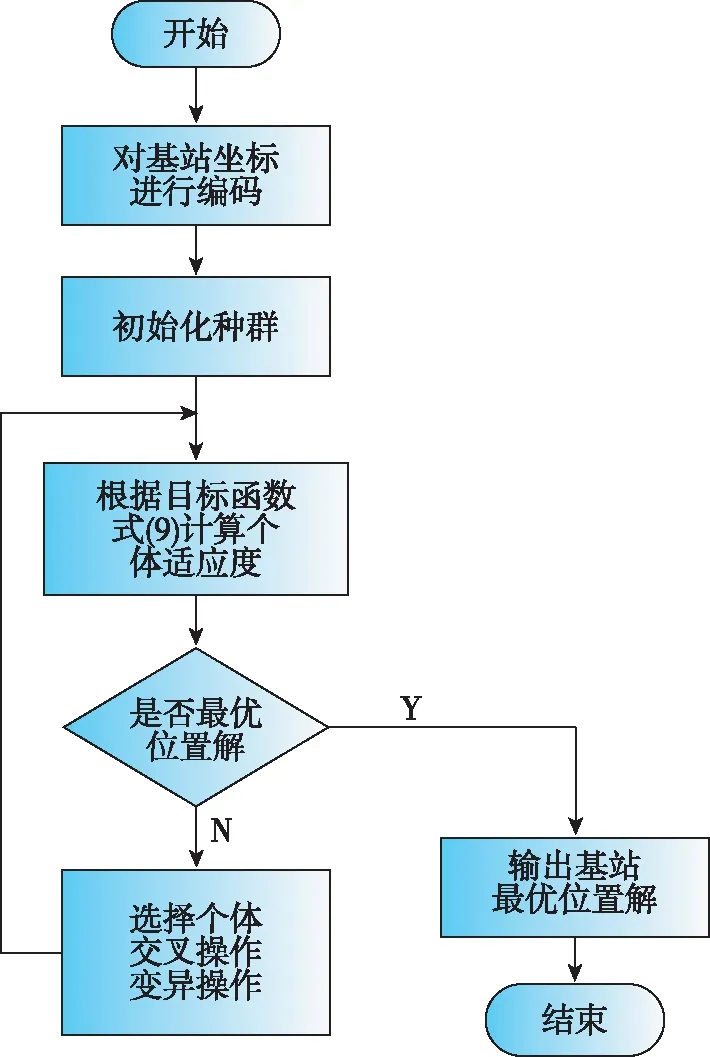
图6 遗传算法流程图Fig.6 Flow chart of genetic algorithm

遗传算法流程如图6所示，通过对基站坐标进行编码，使用目标函数式(9)进行适应度计算，经过个体选择、交叉、变异之后，得到基站优化二维坐标(X,Y)，而通常室内蓝牙基站采用吸顶式安装，基站安装高度为室内空间高度，即Z=H。则可以确定基站的三维坐标(X,Y,Z)。

2 带阈值的EMA误差修正算法

针对行人行走规律，以文献[12]提供的身高为170cm男子步行数据为例，如图7所示，其中A、B、C点分别表示男子右脚抬起、右脚落地、左脚抬起的行走动作。步行平均速度为0.9193m/s，速度幅度变化为0.2m/s，角速度为7.954rad/s。两足支撑时间为0.4s，单足支撑时间为0.45s。

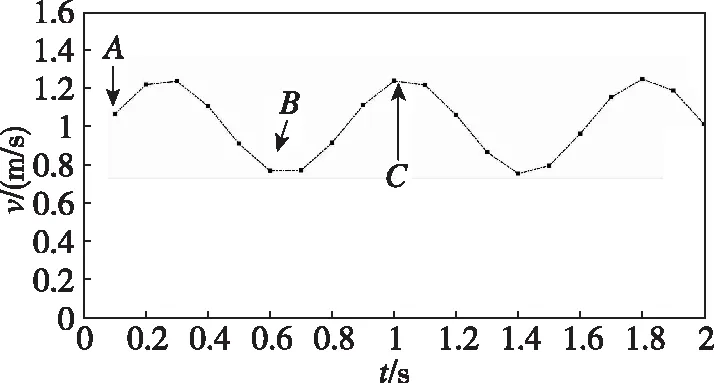
图7 170cm男子行走速度分布示意图Fig.7 Diagram of walking speed of a 170cm male

行人在室内的运动方向为随机事件，具体如图8(a)所示，圆心P表示行人上一时刻的位置，虚线代表行人可能行走的方向。从图8中可以看出，行人可以选择向任何方向前进，由于行人步长和上一时刻的位置P(xt-1,yt-1,zt-1)已知，如图8(b)所示，因此可以估计行人运动到下一位置与基站之间的夹角最大值φmax为

φmax=arcsin(d/BP)

(10)

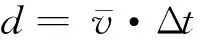
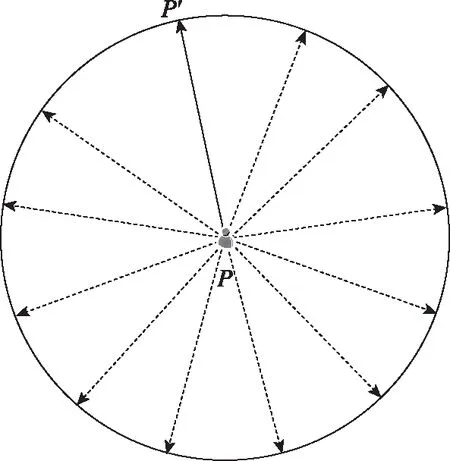
(a)行人运动方向示意图

(b)行人运动与基站之间形成夹角示意图图8 行人方向与基站夹角Fig.8 Angle between pedestrian movement direction and base station

为判断当前位置测量值的可靠性，将行人上一时刻位置P处的测量角度θt-1与当前位置的测量角度θt相减，与φmax进行比较，若两者之差值小于threshold(ε)，表示当前测量值可信，用Y表示；当两者之差值大于threshold(ε)，表示当前测量值具有较大偏差，用N表示，对当前测试点进行重采样，采用EMA算法更新该点测量值。

(11)

为消除测量偏差，本文对EMA算法进行改进，引入阈值对角度信息进行处理，根据行人在室内的运动轨迹判别该点测量值可信度，如式(11)所示。若该点的测量值不可信，表示该点与真实值之间存在较大偏差，将本次测量值舍弃，对该点进行重采样，采集n组测量数据，使用EMA算法进行处理，EMA算法具体如下：

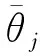
(12)

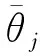
(13)

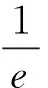
(14)

其中，η为测量误差量，为高斯白噪声。

通过带阈值EMA算法处理后的测量数据更接近真实值，结合EKF算法估计目标位置，建立对应状态方程如下

(15)

(16)

(17)

其中，β1、β2、α1分别为基站1与基站2测量所得方向角、基站1测量所得俯仰角；(x,y,z)为待测目标位置坐标；(Xi,Yi，Zi)为第i个基站的坐标，其中(i=1,2…N,N≥2)。

建立对应观测矩阵H

(18)

其中

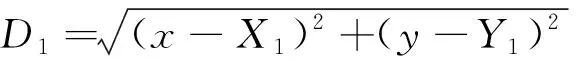
3 实验结果分析

3.1 基站分布对定位精度影响对比实验

本文采用的硬件设备如下：蓝牙芯片为nRF-52832，主控芯片为STM32F103C8T6，具体参数如表1所示。

表1 蓝牙设备具体规格参数

针对基站分布对定位精度的影响进行研究，室内放置障碍物，如图8所示，障碍物参数如表2所示。

表2 实验场地参数表

其中，障碍坐标指障碍物离坐标原点最近的点的坐标，将以上参数代入式(9)，使用遗传算法求取基站坐标，如图9所示。

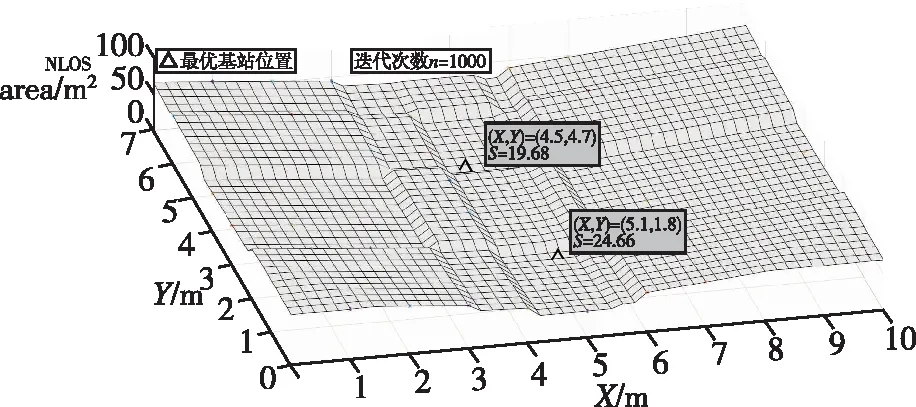
图9 遗传算法求得基站坐标图Fig.9 Base station coordinates obtained by genetic algorithm

为比较本方案的定位性能，进行不同基站安装对比实验，基站方案如表3所示。

表3 三种基站位置坐标表

与表3相对应的基站安装如图10所示，其中，第三种基站布设方案为本文所提方法。

(a)方案1

取室内场景中7个测试点对三种基站分布方案分别进行实验，针对每个测试点，对2个基站所测角度误差进行平均，结果如图11所示。

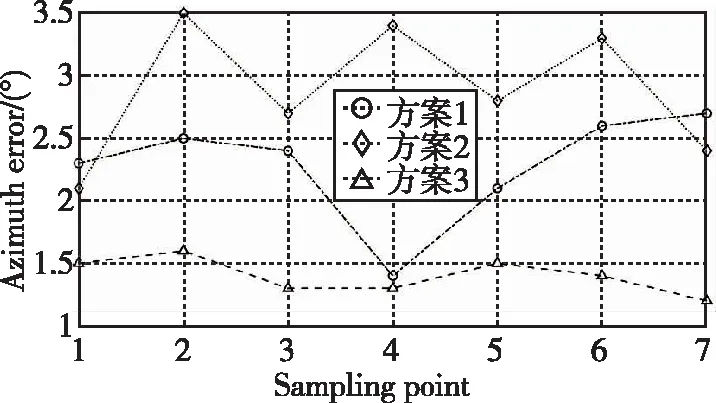
(a) 方位角误差对比

由图11可知，本文所提方法(方案3)的角度测量误差更小，说明在同等环境下，通过本文所提方法进行基站布设，能有效提高角度测量精度。对三种方案分别进行定位实验分析，采用基本的EKF算法进行定位，结果如表4所示。

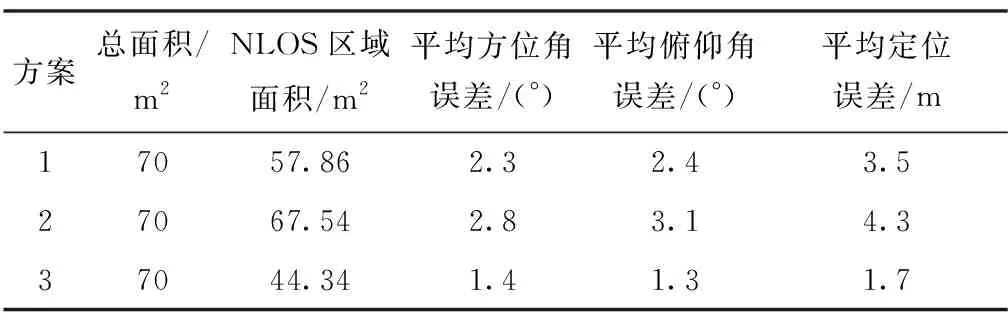
表4 不同基站布置方案测试结果对比表

由表4可知，在同样环境下，本文所提基站布设方案(方案3)NLOS区域为44.34m2，相较于方案1、方案2分别减少了23%、34%；本文所提方法的方位角平均测量误差为1.4°，相较于方案1、方案2分别减少了39%、50%；平均俯仰角测量误差为1.3°，相较于方案1、方案2分别减少了46%、58%。且从定位精度分析可知，同等工况下本文所提方法(方案3)的定位精度明显高于方案1、方案2，说明了本文所提基站布设方案能有效提高室内定位精度。

3.2 改进的EMA/EKF定位算法对比实验

结合本文所提基站布设方案，对本文提出的改进的EMA/EKF算法定位性能进行验证，实验场景为实际室内(10×7)m2的办公场景，如图12(a)所示。

在实验场景中，如图12(b)所示，室内有一条总长13m、宽1.8m 的过道，该过道有较多行人经过或逗留，行人平均身高175cm，采用本文第1章中提出的基站优化理论，解算出该场景下基站A、B的坐标如表5所示，然后进行EMA/EKF定位算法实验。

(a) 实际实验场景图

表5 办公场景下的基站优化分布

实验场景内有办公桌，并有行人在室内自由活动，身高170cm的男子在室内运动轨迹如图13所示，取threshold(ε)=φmax/2，该值为经验值，通过预实验获取。

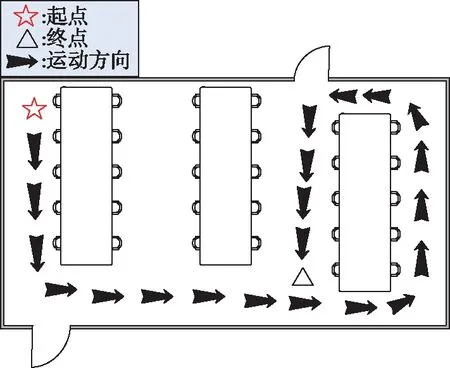
图13 运动轨迹图Fig.13 Motion trajectory diagram

从图14可以看出，本文所提算法定位轨迹更接近于真实的行走轨迹，特别是当待定位人员周围出现较多行人，对待定位人员发出的蓝牙信号产生遮挡时，使用EKF解算出的待定位行人位置出现较大偏差，轨迹出现较大的偏移，而本文所提方法能有效地抑制此偏差，提高定位精度。

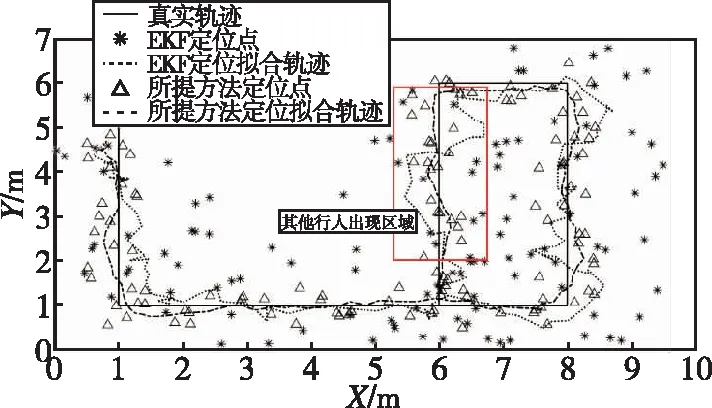
图14 本文所提方法定位轨迹与EKF算法定位轨迹对比Fig.14 Comparison between the positioning trajectory of the proposed method and that of EKF algorithm

将本文所提方法与EKF算法的定位误差进行对比，如图15所示，本文所提方法定位误差曲线低于EKF算法定位误差曲线，且使用EKF算法进行定位存在位置跳变的情况，而本文所提方法解决了这一问题。为进一步说明本文所提算法的有效性，自定义阈值检测率进行定位性能检验，定义如式(19)所示。

(19)

其中，T为总的测量次数；t为测量值超过阈值的次数。

图15 本文提出方法与EKF定位误差对比Fig.15 Comparison of positioning errors betweenthe proposed method and EKF

本文所提方法与EKF定位算法性能对比如表6所示。

如表6所示，本文所提方法的阈值检测率为76%，平均定位误差为0.89m，最大定位误差小于1m，定位性能优于EKF算法，说明了本文提出方法的有效性。

表6 本文所提算法定位性能分析表

4 结论

本文针对室内蓝牙定位易受障碍物遮挡等影响定位精度的问题，从两个方面进行研究以提高系统定位性能：1)通过对蓝牙基站布设位置与接收信号范围关系进行研究，根据室内环境优化基站的布设位置，增加基站信号视距接收范围；2)在基站优化的基础上，根据行人行走规律，提出了改进的EMA算法，结合EKF算法对室内环境中的行人位置进行解算，并对定位误差进行补偿，以提高系统定位性能。通过实验验证，本文提出的方法有效增加了基站信号接收覆盖范围，而且所提算法定位结果明显高于EKF算法，解决了采用EKF定位过程中出现的位置跳变问题，证明了所提方法的有效性。