一种非视距信号环境下智能手机速度平滑定位方法

蒋长辉，陈育伟，Juha Hyyppa

(芬兰地球空间研究所遥感与摄影测量部, 芬兰 埃斯波 FI-02450)

0 引言

芯片级全球导航卫星系统(Global Navigation Satellite System，GNSS)接收机一直是智能手机的重要组成部分[1]。智能手机GNSS接收机可以提供三维位置信息，支持各种基于位置的服务应用(Locat-ion-Based-Service，LBS)[1]。然而，在以高楼为特征的城市地区，受天线限制，智能手机GNSS信号质量较差，在信号恶劣的环境下定位精度有时会下降。具体来说，城市地区的GNSS信号传输路径受多径(Multi-Path，MP)、非视距(None-Line-Of-Sight，NLOS)信号等多种因素的影响。MP是指GNSS接收机同时收到了反射信号和直射信号，两个信号混和在一起；NLOS是指GNSS接收机接收到反射信号，而没有接收到直射信号。额外的信号传输路径会引起高达数十米的位置偏差，这是导致城市地区智能手机GNSS定位精度降低的主要因素[2-4]。

在智能手机GNSS接收机中，通常使用最小二乘法(Least Square，LS)完成位置、速度和时间(Position Velocity and Time，PVT)的计算[5]。在 LS 方法中，PVT的计算是基于最小化测量残差的规则进行的。在城市复杂环境下，NLOS造成的伪距偏差会污染测量并导致位置偏差[4]。就其本质而言，LS方法忽略了位置和速度之间的内在关系。事实上，在NLOS条件下，速度更值得信赖，可以用来平滑位置。卡尔曼滤波器(Kalman Filter，KF)是计算 PVT信息的另一种方法，其规则是最小化均方误差[5]。KF相对于LS而言，结合运动模型利用速度信息对位置信息进行平滑。具体来说，首先构建位置-速度状态传播模型，通过这种方式利用速度信息平滑位置估计[6]。由于信号的反射对导航信号多普勒频移影响相对更小，速度比位置更准确，在KF中采用状态传播模型的预测信息，期望得到更平滑和更准确的解。然而，KF 忽略了这些状态的时间相关特性，这些状态通过速度信息高度相关。KF以递归方式工作，在估计当前状态时忽略过去的历史信息[6]。

因子图优化(Factor Graph Optimization，FGO)方法在同步定位和制图(Simultaneous Localization and Mapping，SLAM)中获得了巨大的成功[7-10]。它利用所有与时间相关的过去测量一起估计所有过去的状态，FGO算法在GNSS位置信息估计中具有巨大的潜力。T.Suzuki在 GNSS 时间相关实时动态(Real-Time Kinematic, RTK)中使用了FGO，并获得了优于KF的位置结果[7]。蒋长辉在GNSS矢量跟踪(Vector Tracking，VT)中实现了FGO，通过在VT 导航滤波器中用FGO代替KF获得了更好的定位结果[9]。此外，在 GNSS中研究了FGO，以提高城市地区位置的稳健性[10-13]。然而，在减小NLOS引起的误差方面，速度并未得到充分利用。尤其是智能手机GNSS，受限于硬件，研究利用速度平滑定位结果具有重要意义。

为了减少城市复杂环境下NLOS信号对智能手机 GNSS引起的位置误差，本文提出了一种基于自适应FGO的智能手机GNSS位置平滑方法，并通过实际场景实验验证了所提算法的性能。

1 模型和方法

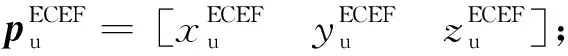
(1)

式中，tb表示GNSS接收机时钟钟差；c表示光速。另外，式(1)中的伪距指矫正过之后的[6]。

1.1 LS

根据式(1)可以计算用户位置，位置增量和伪距增量之间的关系可以表示为

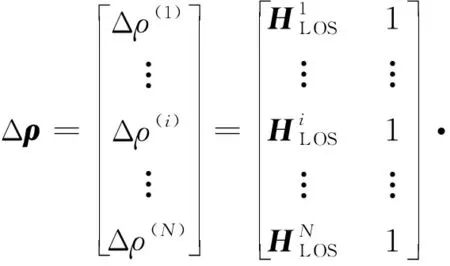
(2)

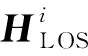
(3)

在NLOS环境下，式(3)可以被写成如下

(4)

式中，bNLOS为NLOS信号造成的位置偏差。通过对比式(3)和式(4)可以发现，NLOS信号导致了位置估计结果的额外偏置。

1.2 KF

KF状态方程建立在用户运动学模型之上，状态方程如下

=Fk,k+1·Xk+wk+1

(5)

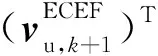
KF量测方程如下

=Hk+1·Xk+1+ηk+1

(6)

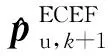
在NLOS环境下，将NLOS信号造成的偏置添加到量测信息，新的模型如下

(7)

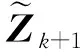
KF更新过程如下

(8)

(9)

(10)

Kk+1=

(11)

(12)

式中，Qk和Rk+1为状态方程噪声协方差矩阵和量测噪声协方差矩阵；Pk和Kk+1为误差协方差矩阵和卡尔曼增益矩阵。

在NLOS环境下，式(10)可以写成如下形式

(13)

从式(13)可以看出，NLOS信号从以下两个方面对KF估计的状态产生影响：1)NLOS信号产生的量测偏置在KF状态更新时降低了状态估计精度；2)信号经过反射之后，量测噪声变大，如果保持量测噪声协方差不变会对状态估计产生消极影响。

2 FGO方法

2.1 因子图构建和模型

在因子图中，通常用边连接因子节点和变量节点。对于给定的测量，状态估计的目的是找到最佳的后验状态估计，可以写成如下形式

(14)

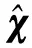
(15)

如上所述，状态估计是基于运动模型和测量模型进行的。基于速度的状态变换和位置测量被建模为两个独立的节点。假设状态过程噪声和测量噪声均服从具有协方差矩阵的零均值高斯分布，可以将状态估计表述为最大后验问题，模型写为

(16)

(17)

(18)

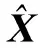
(19)

基于式(5)～式(7)列出的状态和测量模型，FGO的图形结构如图1所示。如前所述，这里有两个因子：运动模型因子和GPS位置因子，详细信息和误差函数如下所示。

图1 因子图结构Fig.1 Structure of the factor graph

(1)运动模型因子

两个连续位置通过速度相关，基于运动模型，两个连续位置表示为

(20)

因此，代价函数可以写成如下

(21)

(2) GNSS因子

GNSS位置信息作为量测，模型如下

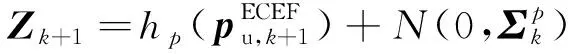
(22)

对应的代价函数如下

(23)

综上，位置的最优估计可以转换成最小化下列代价函数

(24)

本文中，采用GTSAM图优化库求解状态的最优估计[14-16]。

2.2 NLOS环境下的鲁棒策略

如上分析，NLOS会导致位置估计的偏差。NLOS环境下的代价函数如下

(25)

从式(25)可以观察到，NLOS产生的偏置会影响代价函数的值，最终影响位置信息的估计。相对而言，卫星导航信号的多普勒频率被信号反射影响较小，因此速度信息理论上相对更准，这里基于速度信息构建残差如下

(26)

在NLOS环境下，残差会越来越大。这里给出两种策略。

(1) 鲁棒核函数

这里将Huber鲁棒函数引入FGO算法以抑制NLOS带来的位置误差，Huber函数定位如下[8]

(27)

式中，x为变量；b为阈值。

(2) 自适应协方差矩阵

如式(26)所示，NLOS信号会造成残差突然变大，自适应协方差矩阵定位如下

(28)

3 实验与分析

本章利用二种不同的手机采集了静态和动态数据，对提出的算法进行验证。这里采用Google手机定位比赛数据集中的一组Google Nexus 5手机静态数据和一组Xiaomi 8动态数据对算法进行进一步的验证和分析。

3.1 静态数据实验

首先采用Google Nexus 5手机采集的静态数据对算法进行测试，采集地点为(37.422578°, -122.081678°, -28m)[11]。该场景中，GPS卫星2、5、12、15、18、20、21、25、26、29、31被用于定位。图2所示为跟踪的卫星信号强度随时间变化，图3所示为标准LS计算的水平位置和速度误差。可以看到，水平位置误差在10m以内，速度误差在0.2m/s以内。图4进一步地给出了水平位置误差分布、定位精度因子和卫星数量变化。50%概率水平位置误差为4.8m；可见卫星数很快稳定到10颗；HDOP值很快收敛到1以内。图5所示为LS、KF和FGO对应的水平位置误差对比，三种方法速度误差方差为0.01，位置误差方差为5。表1所示为以上三种方法对应的水平位置误差统计分析。从统计分析结果可知，经过KF平滑之后的位置误差均值和均方根降低了19.8% 和19.6%；经过FGO算法平滑之后的位置误差均值和均方根进一步降低了40.1% 和26.3%。图6给出了水平位置误差的概率分布，和KF算法相比，50%和90%概率位置误差减少了48.7% 和28.8%。

图2 卫星信号载噪比Fig.2 Satellite signal C/N0

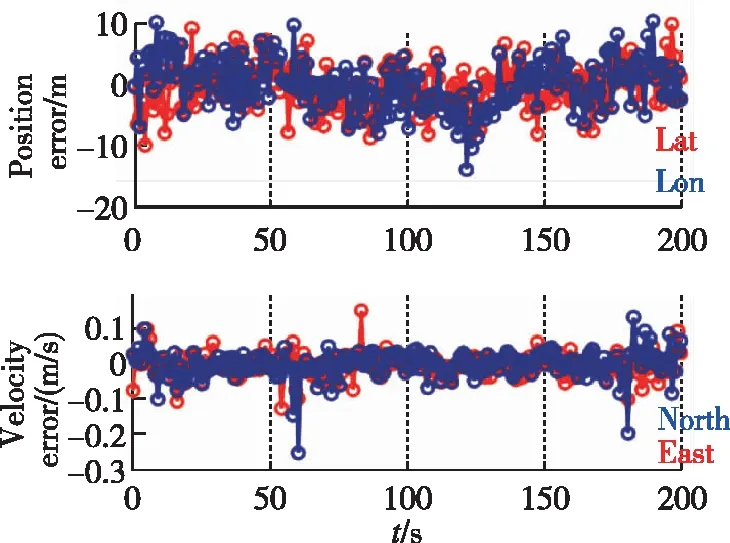
图3 水平位置和速度误差Fig.3 Horizontal position and velocity errors

图4 水平位置误差分布、HDOP和卫星数Fig.4 Horizontal position distribution, HDOP and satellite amount

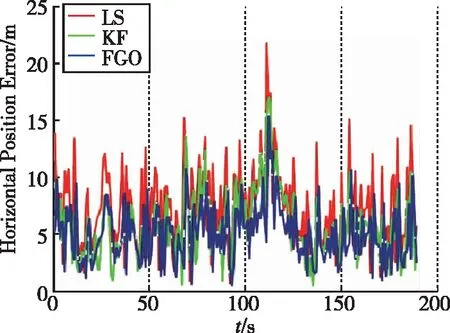
图5 Nexus 5定位误差对比Fig.5 Comparison of Nexus 5 horizontal position errors

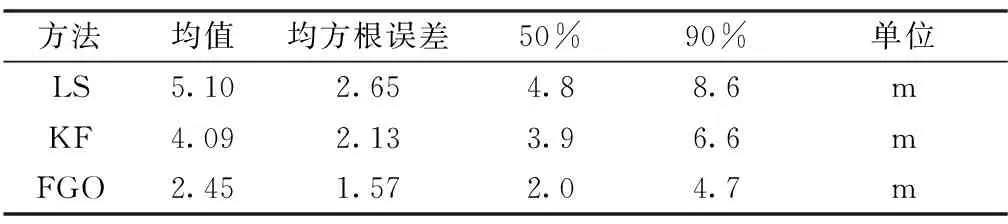
表1 定位误差统计分析

这里在量测位置上加上固定偏差30m,以模拟NLOS场景造成的位置误差，图7所示为该场景下的位置误差对比。图7(a)为模拟从100s开始的10s NLOS场景下的FGO-Huber和自适应FGO的定位误差；图7(b)和图7(c)分别为从100s开始的20s和30s NLOS场景下的定位误差对比。从图中的位置误差曲线可以看出，FGO-Huber和自适应FGO算法可以有效地消除NLOS信号对水平定位精度的影响。在10s和20s NLOS场景下，FGO-Huber和自适应FGO定位误差类似；但是当NLOS时间变长时，自适应FGO算法效果更好，可以有效地减小最大定位误差。

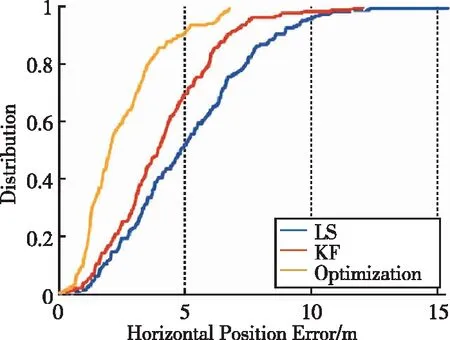
图6 水平位置误差概率分布Fig.6 Probability distribution for horizontal position errors

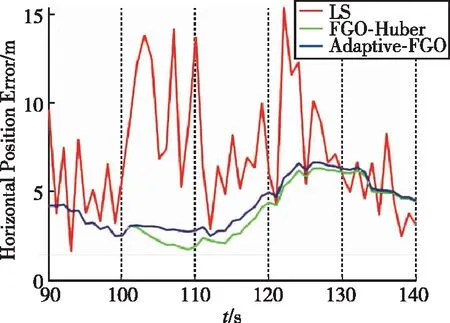
(a) 10s NLOS定位误差

3.2 动态数据实验

进一步采用另一组Google手机定位比赛动态数据评估算法的有效性。此数据采用Xiaomi 8手机装在车上采集，轨迹如图8所示。位置误差随时间变化如图9所示，FGO算法定位误差最小。详细的定位误差统计分析如表2所示，和LS相比，KF和FGO算法的位置误差均值减少了16.4%和39.3%，位置误差均方根误差也有不同程度的减少。

图8 动态实验轨迹图Fig.8 Dynamic trajectory

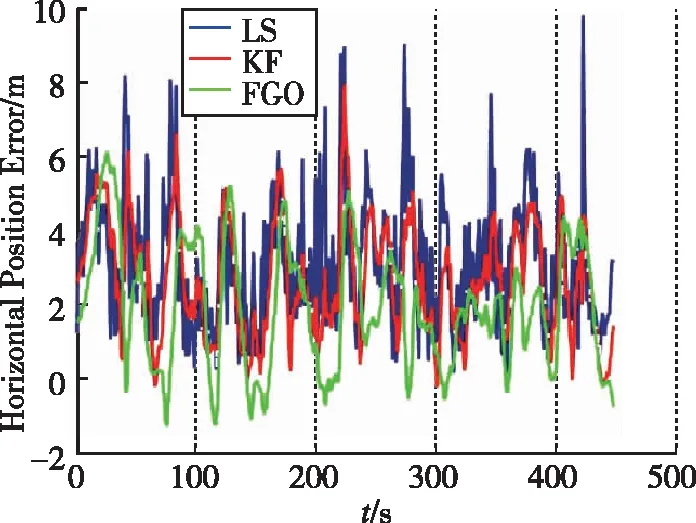
图9 水平位置误差对比Fig.9 Comparisons of horizontal position errors

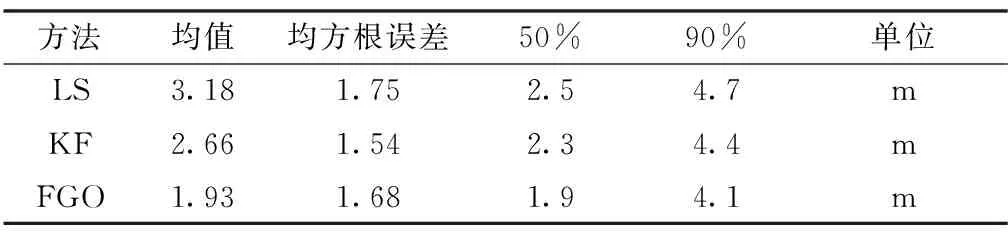
表2 水平定位误差统计分析

和静态实验类似，在轨迹200s开始增加30m恒定误差模拟NLOS信号造成的位置偏差，以评估算法在动态轨迹下的性能。图10给出了从第200s开始的10s、20s和30s NLOS环境下的不同算法定位误差对比。从图中位置误差可以看出，LS和KF结果被NLOS影响较严重，尤其是长时间NLOS信号导致LS和KF定位结果位置误差异常，最大达40m左右。KF-Huber和自适应KF对NLOS造成的误差有一定的抑制作用，但是当NLOS时间变长时，最大定位误差仍然在变大，本实验中最大误差达到了40m。实验结果证明了Huber鲁棒核函数和自适应策略对NLOS误差具有一定的抑制作用。对于10s NLOS场景，FGO-Huber和自适应FGO可以有效地抑制NLOS造成的位置误差异常；但是当NLOS时间变长时，FGO-Huber效果有所下降，在20s和30s NLOS场景下，FGO-Huber算法的最大位置定位误差大约达到了30m和43m,证明了本文提出的算法对NLOS误差的抑制作用。

4 结论

针对城市复杂环境下NLOS信号对智能手机定位精度的影响，本文基于因子图框架和运动模型构建位置优化方法，并提出了FGO-Huber和自适应FGO方法抑制NLOS造成的位置误差。通过静态和动态实际场景实验证明了所提算法可以有效地减少NLOS信号造成的位置误差。根据实验结果可以得出以下结论：

1)采用速度优化可以平滑定位结果，FGO算法可以有效地提高智能手机的GNSS定位精度；静态实验中，KF平滑之后的位置误差均值降低了19.8%；经过FGO算法平滑之后的位置误差均值进一步降低了40.1%；动态实验中，和LS相比，KF和FGO算法的位置误差均值减少了16.4%和39.3%。

2)自适应协方差矩阵结合FGO方法可以有效地克服NLOS信号对智能手机GNSS水平定位精度的影响，提高智能手机GNSS在城市复杂环境下的定位精度；动态实验中，在10s、20s和30s NLOS环境下，自适应FGO算法可以一直抑制NLOS造成的位置误差，而FGO-Huber等方法在20s和30s NLOS时长下，位置误差逐渐变大，最大达到43m。