高铁地震信号衰减特征分析及震源函数验证
贾宝新, 周志扬, 苑文雅
(1.辽宁工程技术大学 土木工程学院,辽宁 阜新 123000; 2.中国地震局地质研究所,北京 100000)
自我国的高速铁路(以下简称“高铁”)建成通车起,高铁的运营里程逐年增长,对沿线城市的经济发展起到了促进作用。受到轨道不平顺等因素的影响,高铁列车在行驶过程中以应力波的形式向周围传播能量,这种应力波被称为高铁地震波。高铁列车作为一种产生的能量较高、频谱较宽且重复性好的震源,高广运等[1-2]首先从振动荷载的角度出发,分析路基及结构物的动力响应。张唤兰等[3-4]对高铁地震信号数据属性进行分析,认为高铁地震信号中富含地质环境信息,利用高铁地震信号探测地质情况乃至地震干涉成像成为可能。为利用高铁地震波对浅层或深层地下结构反演,温景充等[5-6]从地震波的传播特性出发,利用求解声波波场等方法,对高铁激发的远场波场进行模拟。张固澜等[7-10]通过震源模型建模和全波形反演建模,为高铁地震波传播规律、属性变化监测和高铁地震数据处理奠定了基础。关于高铁地震信号的特征研究问题,多数研究者通过不同的分析方法,得到高铁地震信号的特征量或时频特征[11-15]。目前,对高铁地震信号的衰减特征分析和反映衰减特征的高铁震源函数研究较少。
本文建立了高铁列车多组点源简化模型,并基于地震波的传播和衰减机理,对高铁震源时间函数进行理论推导,进而合成可以反映高铁地震信号能量衰减特征的高铁震源函数。通过现场监测试验,分析高铁地震信号振动速度和能量的衰减特征,总结了高、低频信号的能量分布规律。对比现场监测的高铁地震信号数据与合成高铁地震信号数据,验证了利用合成高铁震源函数反映高铁地震信号能量衰减特征的可行性。
1 高铁震源函数
从固定点源的Green函数[16]出发,将移动的高铁列车简化为移动的多组点源模型:高铁轨道为x轴,高铁运行方向设置为x轴正方向;y轴垂直高铁轨道线,监测点布置一侧设置为y轴正方向。通过Green函数和震源时间函数的褶积,可以得到移动震源作用下某一监测点的位移函数
U(x,t)=G(x,t;ξ,τ)⊗S(t)
(1)
式中:U(x,t)为监测点x(x0,y0)处在t时刻的位移;G(x,t;ξ,τ)为τ时刻位于ξ处的震源点作用下监测点x(x0,y0)的位移;S(t)为高铁列车的震源时间函数,可为任意的周期性地震子波。
将列车车轮与轨道之间的接触方式视为多组点与线的接触,高铁列车可简化为沿x轴正方向移动的多组移动点源。假设高铁列车共有N节车厢,以匀速v运行,每节车厢的长度均为L,由于高铁列车整车长度远大于车厢间连接处,因此将实际车厢和连接处的总长度近似视为整个模型车厢的长度,则整列高铁作为震源产生的地震信号是N节车厢的多组车轮作为点震源每隔时间段L/v激发形成的。基于此,首先建立单节高铁车厢的震源模型,车厢前后有4组轮对,其中第1、第2组轮对组成轮组1,第3、第4组轮对组成轮组2,将a和b分别表示为轮组的前后轮对间距和前后轮组的间距,高铁车厢行驶时,设车厢的第1组轮对通过坐标原点的时刻t=0,高铁震源模型如图1所示。

图1 高铁震源模型Fig.1 Source model of high-speed-train
首先表示N节车厢第1组轮对的震源时间函数,采用冲激型震源时间函数突出高频特征,更好地反映高铁地震信号的宽频特征
(2)
N节车厢的4N组轮对的震源时间函数可以表示为整列高铁列车的震源时间函数
(3)
高铁地震波的衰减受传播介质的性质和地震波扩散范围的影响,这两种影响因素下的衰减称为材料阻尼衰减和几何阻尼衰减。实际情况下,对高铁地震信号的衰减特征分析需同时考虑两种衰减的影响。
考虑材料阻尼衰减,不同位置岩土介质的特性不同,造成不同位置的高铁地震波能量衰减特征存在差异。利用材料阻尼衰减系数α描述由于岩土介质特性差异导致的衰减程度差异,高铁地震波的材料阻尼衰减表示为
A=A0e-α(r-r0)
(4)
(5)
式中:A和A0分别为r和r0位置处的振幅;α为材料阻尼衰减系数;α0为地基土的衰减系数,天然地基土的α0值随土体的改变而改变;f为高铁震源频率,Hz;v为高铁移动速度,m/s。
不同地基土的衰减系数α0参考表1选取[17]。
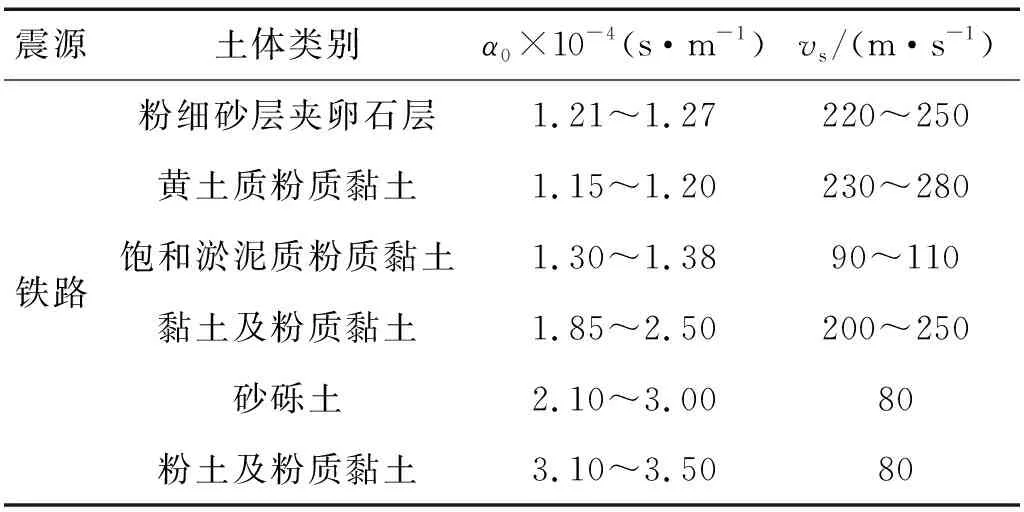
表1 地基土衰减系数α0
考虑几何阻尼衰减,使用基于三维均匀空间声波方程的Green函数近似表示高铁地震波的扩散
(6)
式中:ξ为τ时刻震源点的位置;τ为高铁沿x轴正方向运行的某一时刻;c为声波波速,m/s;x(x0,y0)为监测点。
综合考虑材料和几何阻尼衰减的影响,高铁震源函数可表示为Green函数和震源时间函数的褶积:
U(x,t)=[G(x,t;ξ,τ)⊗SN(t)]×e-α(r-r0)
(7)
2 高铁地震信号衰减特征分析
2.1 高铁地震信号监测试验
在京沈高铁阜新段进行监测试验,现场土体类型为辽西风积土,天然密度ρ为1.80 g/cm3,干密度ρd为1.55 g/cm3;其力学性质介于饱和粉质黏土和粉质黏土之间,在深度20 m内土体的平均剪切波速vs为244.6 m/s,衰减系数α0为1.31×10-4~2.32×10-4s/m。
使用超高频构造活动监测仪(Antenna-Ⅲ),其通过传感器、传输电缆、数据集线器、转换器和主机的连续采集,可以将高铁地震信号数据生成原始记录文件(*.HFMED)和压缩索引文件(*.HFIdx),可观测震级范围为-3~2级,采样频率最高可达100 kHz,对信号频带在10.0 Hz~1.4 kHz的振动信号平坦响应,能够有效监测高铁地震信号。
选取高铁桥梁周边布设传感器,传感器以嵌入式固定在地表并通过石膏固定。设置5条监测线路,每条监测线路同时布置6个传感器并分别设定为1号传感器~6号传感器,以传感器与高铁线路的垂直距离为震源距,传感器布置监测方案如表2所示。监测仪器及监测现场如图2所示。

表2 传感器布置监测方案

图2 监测仪器及监测现场Fig.2 Monitoring instrument and monitoring site
2.2 振动速度衰减特征
通过对现场监测的高铁地震信号波形最大幅度值的识别,得到各次试验高铁地震信号的峰值质点振动速度,如表3所示。以1号传感器的峰值质点振动速度为基准,根据表2和表3中各传感器峰值质点振动速度及其与震源的距离,计算得出各传感器相对于1号传感器的峰值质点振速衰减比例,结果如图3所示。

表3 峰值质点振速
基于图3衰减比例的分析可知,5次监测的振动速度衰减趋势基本一致,其中距离震源5~15 m内的平均峰值质点振动速度衰减比例为69.7%,约为15 m范围外的平均峰值质点振动速度衰减程度的3.5倍,距离震源100 m范围外高铁地震波的振动速度趋于稳定,平均峰值质点振速衰减比例为90.2%。传感器与震源距离越大,高铁地震信号的峰值质点振动速度表现出不断衰减的明显特征,且离震源越近的峰值质点振速衰减程度越大。
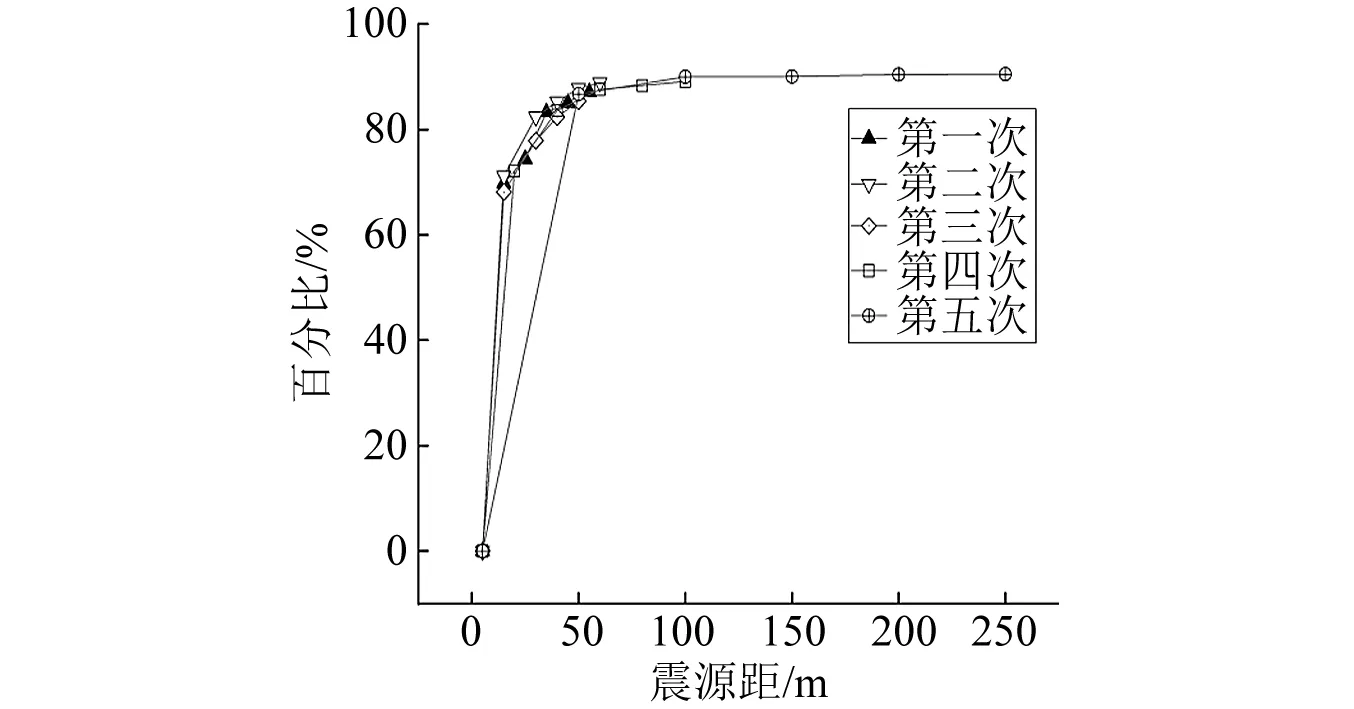
图3 峰值质点振动速度衰减比例与震源距关系Fig.3 Relationship between peak vibration velocity of high-speed-train seismic signal and ranging
从高铁地震波的振动速度衰减特征分析可以得出,距离震源100 m的范围内,高铁地震波的振动速度衰减了约90%,由于受到岩土介质的特性和地震波扩散作用的影响,振动的大部分动能传递到铁路路基的岩土介质中,此现象与高铁地震波的衰减理论相符。
2.3 瞬时能量衰减特征
利用MATLAB软件探究不同位置处的高铁地震信号瞬时能量的衰减特征,选取第一次监测中1号传感器~6号传感器接收的高铁地震信号,通过HHT(Hilbert-Huang tansform)变换得到高铁地震信号的瞬时能量谱,如图4所示。
从图4可知,传感器与震源距离越大,高铁地震信号瞬时能量谱的峰值越小。瞬时能量谱具有多个峰值,传感器与震源距离越大,各个瞬时能量峰值越分散,即瞬时能量峰值出现的间隔时间越长。瞬时能量谱中存在一个或几个峰值明显高于其他峰值,5号和6号传感器监测到高铁地震信号的各个瞬时能量峰值之间已经相差不大,即距离震源45 m范围外没有明显的瞬时能量峰值。拾取图4中各瞬时能量谱的瞬时能量峰值,计算得出各传感器相对于1号传感器的瞬时能量峰值衰减比例,如表4和图5所示。

图4 瞬时能量谱Fig.4 Instantaneous energy spectrum

表4 瞬时能量峰值衰减比例
由图5可知,距离震源5~15 m内瞬时能量峰值衰减比例为90.23%,约为15 m范围外瞬时能量峰值衰减比例的14倍。对比相邻两传感器的瞬时能量峰值,4号传感器的瞬时能量峰值较3号传感器的瞬时能量峰值增大14.37%,6号传感器的瞬时能量峰值较5号传感器的瞬时能量峰值增大52.68%,这是由于试验中的岩土介质由上部覆土层和下部岩石层组成,高铁地震波穿过土层在岩层表面反射、滑行和折射后与沿地表前进的表面波同时作用于同一位置,几种波的叠加产生了局部振动增大的现象,局部增大的位置与土层厚度、阻尼比、波阻抗比等因素有关。

图5 瞬时能量峰值衰减比例与测距关系Fig.5 Relationship between instantaneous energy peak attenuation ratio and ranging
对比分析图3和图5可知,高铁地震信号在岩土介质的振动速度和瞬时能量的衰减比例都与震源距离呈正相关,二者的衰减趋势一致。相比于峰值质点振动速度,瞬时能量峰值的衰减程度更大且衰减速度更快。
从微观的角度看,高铁地震波的传播是介质粒子振动现象的体现,当某处介质粒子离开平衡位置,该粒子在弹性力的作用下会发生振动,同时又引起周围粒子的振动,因此高铁地震波的能量传递实际是介质粒子动能和势能的传递。从能量的角度看,高铁地震信号在岩土介质中传播的本质是能量的转换,即高铁地震信号振动能量的衰减和岩土介质能量的吸收,高铁地震信号振动能量的衰减包括振动动能的衰减和振动势能的衰减,其中振动动能的衰减是振动速度减小的主要原因,振动势能的衰减是造成振动速度和瞬时能量衰减程度和衰减速度产生差异的主要原因。
2.4 各频率的能量衰减特征
通过EMD( empirical mode decomposition)法选取高铁地震信号,分别筛选IMF(intrinsic mode function)分量中的高、低频分量,计算并使用MATLAB软件输出边际谱。信号边际谱表明了每个瞬时频率点的累积幅值(能量)分布,边际谱中的某个频率点上存在着能量时,表明某一时刻此频率的波有较高的可能性出现。选取第一次监测中1号传感器~6号传感器接收的高铁地震信号,高铁地震信号的边际谱如图6所示。
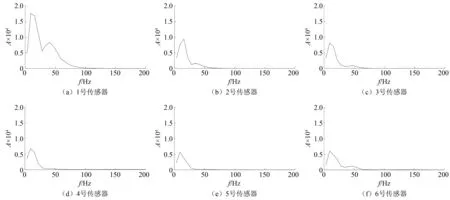
图6 边际谱Fig.6 Marginal spectrum
由图6可知,高铁地震信号的边际谱主要集中在0~100 Hz。除2号传感器的高铁地震信号的边际谱峰值对应频率为15.630 Hz,其他高铁地震信号的边际谱峰值对应频率均为9.375 Hz,本监测试验中高铁地震波的能量峰值频率集中在9.375~15.630 Hz。从整体看,传感器与震源的距离越大,高铁地震信号边际谱峰值越小。
边际谱高、低频有明显的分段,以0~25 Hz为本试验的边际谱低频段,以25~100 Hz为本试验的边际谱高频段。边际谱在低频段和高频段各有一峰值,高频段峰值在4号传感器、5号传感器的高铁地震信号边际谱中不明显,在6号传感器的高铁地震信号边际谱中重新出现,低频段峰值远大于高频段峰值,这也表明高铁地震信号的能量主要分布在低频段。拾取图6中边际谱高、低频段的峰值,计算出各传感器相对于1号传感器的边际谱峰值衰减比例,如表5和图7所示。

表5 边际谱峰值衰减比例
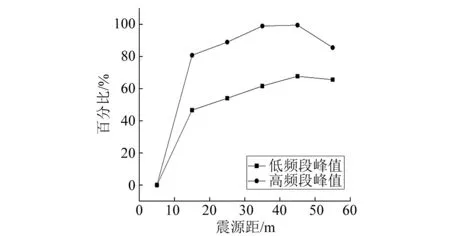
图7 边际谱峰值衰减比例与测距关系Fig.7 Relationship between peak attenuation ratio of marginal spectrum and ranging
分析图6和图7可知,6号传感器高铁地震信号的高、低频段峰值产生了增大的现象,表明距离震源55 m处高铁地震信号能量的增强,此特征与瞬时能量衰减特征分析相符。传感器与震源的距离越大,高频和低频段峰值衰减程度越小,其中高频段信号的能量比低频段信号的能量衰减速度更快,低频段信号的能量比高频段信号的能量衰减更多,造成低频段信号的能量占比不断提高:低频段信号的能量与高频段信号的能量之比从2.12 ∶1提高到5.04 ∶1。这是由于低频段信号较高频段信号能量更多、衰减速度更慢,造成低频段信号的能量占比不断提高。
3 高铁震源函数的验证
采用MATLAB Curve Fitting Tool,分别对现场监测的实际高铁地震信号和合成高铁地震信号的瞬时能量峰值衰减程度进行拟合,验证合成高铁地震信号是否能够反映能量衰减特征。本高铁震源函数的验证中土体衰减系数α0取均值1.82×10-4s/m,高铁震源频率f取9.375 Hz,高铁移动速度v取83.3 m/s,使用式(7)合成高铁地震信号;由于式(7)中未考虑实际岩土介质分层的影响,因此在实际高铁地震信号瞬时能量峰值的拟合中去除瞬时能量增大位置的峰值;以具有8节车厢的高铁列车为例,高铁震源函数验证图,如图8所示。其中:图8(a)为基于式(3)的冲激型震源时间函数,图8(b)为基于式(6)的Green函数和震源时间函数褶积成的位移函数;图8(c)为叠加噪声并考虑几何阻尼衰减的距离震源5 m处的合成高铁地震信号;图8(d)为试验监测的距离震源5 m处的实际高铁地震信号,图8(e)为合成高铁地震信号的瞬时能量峰值衰减程度与震源距对应关系的拟合;图8(f)为实际高铁地震信号的瞬时能量峰值衰减程度与震源距对应关系的拟合。
对比图8(c)和图8(d),合成高铁地震信号与实际高铁地震信号的相似度较高,二者均具有相似的振幅峰值和振幅峰值间隔时间,这表明式(3)的冲激型震源时间函数可以有效反映实际高铁地震信号的振幅峰值特征,且通过式(1)和式(7)的高铁震源函数合成高铁地震信号是可行的。相比于图8(d)的实际高铁地震信号,图8(c)在0~1 s内存在无信号段,这是由于实际高铁连续运行,因此实际高铁地震信号也是连续的,而高铁列车震源模型由静止开始运行,造成合成高铁地震信号是非连续的。

图8 高铁震源函数验证图Fig.8 Verification diagram ofhigh-speed-train source function
对比图8(e)和图8(f):瞬时能量峰值衰减的趋势基本一致,验证了合成高铁地震信号可以反映能量衰减特征;但相比于合成高铁地震信号,实际监测的高铁地震信号能量衰减程度更大并且衰减速度更快。主要原因是:实际高铁地震信号频谱较宽,既包含了低频信号也包含了高频信号,因此仅用单一震源频率值合成的高铁震源函数不能精确表示能量的衰减程度,为了使合成高铁地震信号的能量衰减更加符合实际情况,需要叠加各个频率处合成高铁地震信号的能量,来反映整体能量的衰减程度。此外,合成高铁地震信号采用的Green函数为三维均匀空间声波方程的Green函数,导致合成高铁地震信号的几何阻尼衰减与实际衰减情况不完全相符。
4 结 论
本文将行驶中的高铁列车简化为移动的多组点源模型,以三维均匀空间声波方程的Green函数和多组点源的冲激型震源时间函数为基础,通过褶积得出高铁震源函数。为验证高铁震源函数是否能够反映高铁地震信号的衰减特征,进行了现场监测试验,从振动速度、瞬时能量谱和边际谱3个角度的分析,得出了高铁地震信号的衰减特征及利用高铁震源函数反映高铁地震信号能量衰减特征的可行性:
(1) 高铁地震信号在岩土介质中传播时,与震源距离越近,振动速度的衰减程度越大;近场高铁地震信号的振动速度减小约90%,振动的大部分动能传递到铁路路基的岩土介质中。
(2) 高铁地震信号在岩土介质中传播时,与震源距离越远,瞬时能量的峰值越小;瞬时能量谱有多个峰值,与震源距离越远,瞬时能量峰值之间的时间间隔越大;距离震源35 m和55 m处存在局部振动增大的现象;振动速度和瞬时能量的衰减趋势一致,振动势能的衰减导致瞬时能量的衰减程度更大且衰减速度更快。
(3) 高铁地震信号在岩土介质中传播时,与震源距离越远,边际谱的峰值越小;高铁地震信号的能量主要分布在低频段,高频段信号的能量比低频段信号的能量衰减速度更快;距离震源55 m处高铁地震信号存在能量增强的现象。
(4) 合成高铁地震信号与实际高铁地震信号有相似的振幅峰值和振幅峰值间隔时间;冲激型震源时间函数可以模拟振幅峰值特征,合成高铁地震信号可以反映能量衰减特征;实际高铁地震信号较合成高铁地震信号能量衰减程度更大且衰减速度更快。
虽然合成高铁地震信号反映了一些实际高铁地震信号的特征,但是二者的相似度还有待提高,未来考虑在振动荷载、材料阻尼衰减系数和成层地基3个方面改进高铁震源函数,进一步探究高铁地震波的传播和衰减机理。此外,由于相同工程结构的用料及特性基本一致,其材料阻尼衰减系数可设为定值,这为研究高铁地震波对工程结构的影响提供了理论基础。本文也初步表明:近场范围内,高铁地震波的高频段能量衰减速度较快,可在较短时间将大部分能量传递给工程结构,因此近场范围内高频段和低频段的高铁地震波对工程结构的影响都不可忽视。

