基于有限体积法的三维稳态渗流计算方法及其应用

宿 晓 辉，张 明 亮，贺 英 芝

(大连理工大学 建设工程学部水利工程学院，辽宁 大连 116033)

0 引 言

渗流分析和渗流控制是大坝工程中极为重要的一项研究内容，直接关系到工程的费用和安全。国内外许多破坏或溃决的工程多数都是由于渗流控制不当所引起的。据不完全统计，中国拥有水库大坝近10万座，其中95%以上为土石坝。这些水库大多兴建于20世纪50～70年代，并且限于当时的技术和经济条件，许多工程均是边勘测、边设计、边施工，这给大坝的安全运行埋下了巨大的隐患。在土石坝失事事故的原因统计中，约有1/2是由于渗流问题所引起的，所以对病险坝进行渗流计算就显得尤为重要[1-4]。

随着计算机技术的高速发展，数值解法在求解渗流问题领域逐渐占据主导地位。常用的数值求解方法主要是有限差分法[5-6]和有限单元法[7-10]，其他方法，如边界元法[11]、无单元法[12]等也有应用。目前，在这些数值计算方法当中，较为流行的是有限单元法的应用[8]，但是其计算工作量大，应用到求解大型工程渗流计算时，耗时较长。有限体积法与有限元相比，计算工作量小，并且其控制体积内局部绝对守恒的特性对于处理流动问题具有更好的性能[13-14]。

近年来GPU并行加速技术发展迅速且已相对成熟，浮点计算能力是同代CPU的10倍以上。NVIDIA等公司发布的较为完善的CUDA和OpenAcc并行编程标准打破了GPU技术应用的瓶颈[15-16]，使得GPU技术应用到多体系统模拟、计算流体力学、核科学等各个计算领域。在水利计算中，GPU并行优化技术已经应用到水动力学模型[17-19]、分布式水文模型[20]、梯级水库调度[16]的求解中，取得了较好效果，而在土石坝渗流计算领域中，目前尚未有研究明确实现GPU并行加速。

基于此，本文提出了基于非结构化网格的有限体积法渗流模型。模型采用预处理共轭梯度算法快速求解代数方程组，使用固定网格变渗透系数法求解计算域内含有浸润面的问题，创建无系数矩阵数值迭代求解方法对渗流控制方程进行离散，应用OpenACC-GPU并行技术加速求解。通过与商用软件GEO-Studio进行结果对比，证明本文提出的模型满足工程渗流实际需要。

1 渗流计算方法和原理

非均质各向异性稳态饱和渗流问题的控制方程为

(1)

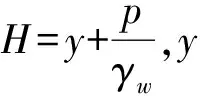
1.1 控制方程离散

采用非结构化网格的有限体积法对渗流控制方程进行离散，采用预处理共轭梯度法(PCG)加速对离散方程求解。采用Cell-Vertex方法形成控制体，并在控制体上对公式(1)进行积分。该方法中四面体单元顶点的控制体如图1所示。对于每一个顶点的控制体，用四面体的中值对偶来实现；四面体单元的顶点分别为A，P，B，C，点O是四面体单元APBC的中心，点a，b，c分别是AP，BP，CP的中点；1，2，3分别为面APC，CBP和ABP的形心；在Cell-Vertex模式中，所有的计算变量值均存储在顶点A，P，B，C上；三角形O1a，O3a，O3b，O2b，O1c和O2c组成了四面体单元中节点P的控制体表面；同样的，构建了剩余节点A，B，C的控制体表面[21]。基于这种思想构造的控制体会在一定程度上降低网格奇异性的影响，提高计算的准确度。

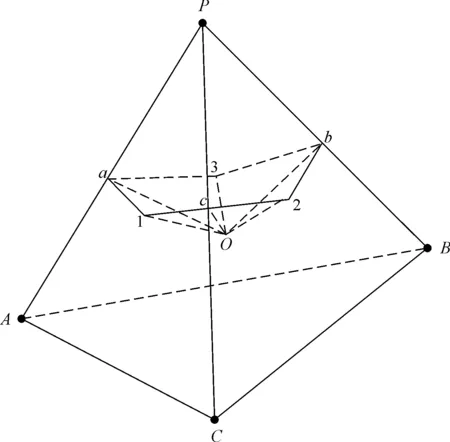
图1 围绕节点P的控制体

对渗流控制方程在上述控制体上进行积分(以P为例)：

∭Vcv∇·FdV=0

(2)

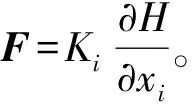
采用高斯散度定理对公式(2)积分：

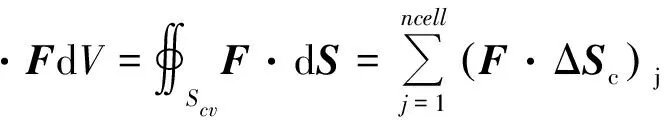
(3)

式中：ncell代表与控制节点P相关联的单元数目，ΔScj表示控制体在四面体单元j中的对应边界面。对于给定的四面体单元，可以采用闭合曲面积分公式计算ΔScj：

ScvdS=0

(4)

在控制体所有边界面法向量积分为0，可以得到：

(5)

将其代入式(3)可以得到：

(6)

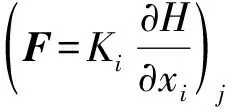
四面体单元的中心梯度是通过单元顶点变量值采用格林公式计算得来：

(7)

四面体单元的中心渗透系数是通过单元顶点渗透系数值采用体积加权法计算得来：

(8)

式中：Hi为四面体单元j中顶点i处的变量值；Si为四面体单元j中顶点i所对应的面的法向量，其大小为顶点i所对应面的面积；V为四面体单元体积；(Ki)m为四面体单元j中顶点m处的渗透系数值。

由式(6)推导可得：

(9)

式中：R(H)为残余误差，当R(H)<ε(ε为收敛控制精度)时，认为计算结果已经收敛，达到所需精度要求。公式(9)同时表明，本文提出的稳态渗流计算方法无需建立二维系数矩阵A，而将AH整合为一列向量，节省了存储空间，减少了内存占用。

本文采用预处理共轭梯度法快速求解代数方程组，其求解步骤为：

(1)给定求解域初始值H0。

(2)通过初始值H0，求得初始残差向量r0，并利用预处理对角阵M-1得到P0。

r0=b-AH0=0-AH0=-R(H0)

(10)

z0=M-1r0

(11)

p0=z0

(12)

式中：M=diag(a11，a22，...，ann)。

(3)对k=0，1，…进行计算，直到收敛完成。

αk=(rk，zk)/(Apk，pk)

(13)

Hk+1=Hk+αkpk

(14)

rk+1=rk-αkApk

(15)

zk+1=M-1rk+1

(16)

βk=(zk+1，zk+1)/(rk，zk)

(17)

pk+1=zk+1+βkpk

(18)

1.2 边界条件

渗流模型应用在土石坝渗流计算时，渗流场在边界上还应满足一定的条件，主要包括以下几种[22-23]。

第一类边界Γ1，即已知常水头边界：

H(x，y，z)=Hfixed(x，y，z)

(19)

第二类边界Γ2，即流量边界条件q0=qfixed，在渗流计算分析中设定q0=0得到不透水边界：

(20)

浸润面Γ3：

(21)

溢出边界面Γ4：

(22)

溢出边界面的位置采用迭代方法获得[22，24]，其计算基本过程如下：

(1)假设溢出面范围。可以设定求解区域下游面上的下游水位以上区域全部为渗流溢出面。

(2)将假设的溢出面给定第一类边界条件。将溢出边界面上节点的总水头给为位置高程，即H(x，y，z)=y。

(3)通过求解渗流方程得到计算域内的总水头分布。

(4)溢出面修正。在计算收敛之后，根据溢出边界面的另一个控制条件即式(23)进行更正：

(23)

(5)将不满足式(22)的溢出面节点从溢出边界面剔除，并将下游面内溢出面以上H(x，y，z)>y的节点归入溢出面范围。

(6)根据修正后的溢出面返回步骤(2)重新进行迭代计算，直到两次迭代计算溢出面节点数之差小于某一给定值，则迭代结束，完成计算。

1.3 固定网格变节点渗透系数

本文使用固定网格变节点渗透系数方法计算域内浸润线存在问题。将浸润线以上节点渗透系数设置为近似不透水情况时，以满足式(21)所设定的控制条件，其主要步骤如下[25]：

(1)假定全区域均为饱和区即H(x，y，z)≥y，各节点渗透系数均为饱和渗透系数，进行初次渗流迭代计算。

(2)初次渗流计算完成后，通过比较节点水头H(x，y，z)与节点坐标y值的大小，将区域分为饱和区与无压区，无压区即浸润面以上的区域，将无压区所有节点的渗透系数降低1 000倍，进入下次迭代计算。

(3)通过不断更新无压区并改变其渗透系数大小，寻找浸润线位置，当无压区节点数量小于控制收敛精度时，得到满足收敛精度下的稳态饱和渗流计算结果。

1.4 GPU并行加速

OpenACC是目前主流的GPU并行加速技术之一，是一种以编译器导语形式实现的GPU并行标准，其优势为减少底层代码的修改实现加速手段。本文通过支持OpenACC加速标准的PGI编译器，采用kernel构件实现本文模型的并行加速计算功能。

2 算例验证

本文采用下面二维均质土坝渗流问题进行模型评估与验证。

假设一二维均质黏土坝[23]，坝底相对高程0 m，坝高50.0 m，顶宽10 m，上游坝坡坡比1∶2，下游坝坡坡比1∶1.5，饱和渗透系数为3.4×10-8m/s，上游水位45 m，下游无水，底面为不透水边界，大坝剖面图见图2，其网格剖分见图3，计算坝体的渗流场分布，计算结果如图4～5所示，并与GEO-Studio(2018学习版)计算结果进行了对比。

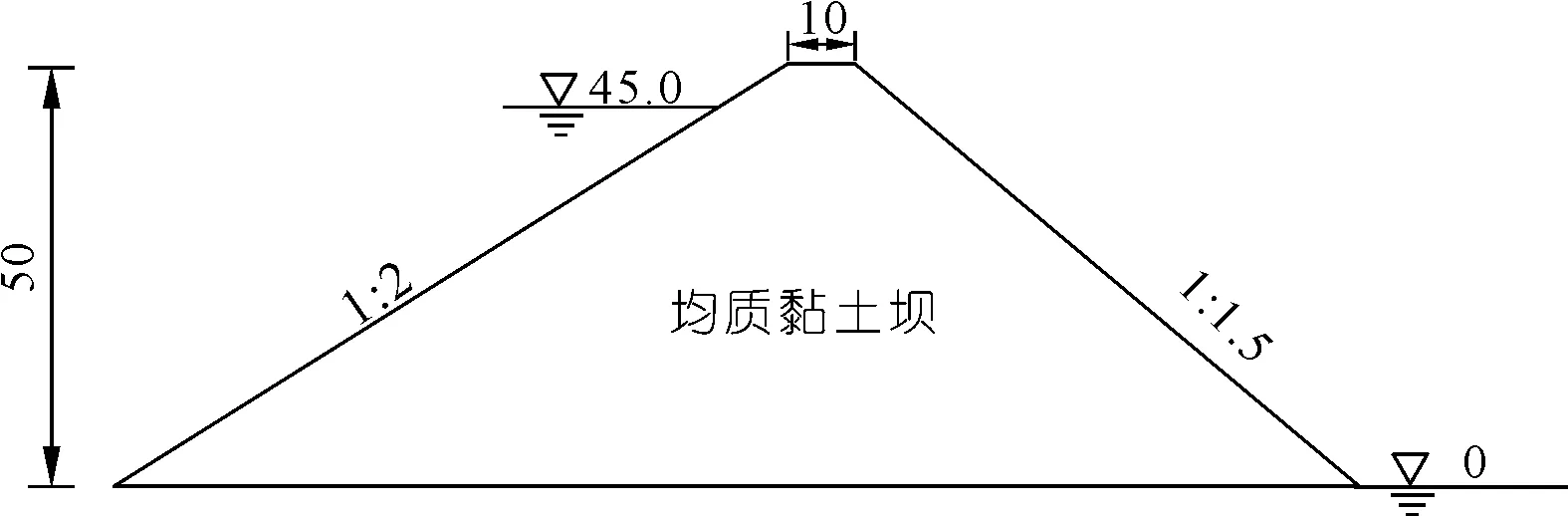
图2 均质黏土坝剖面图(尺寸单位：m)

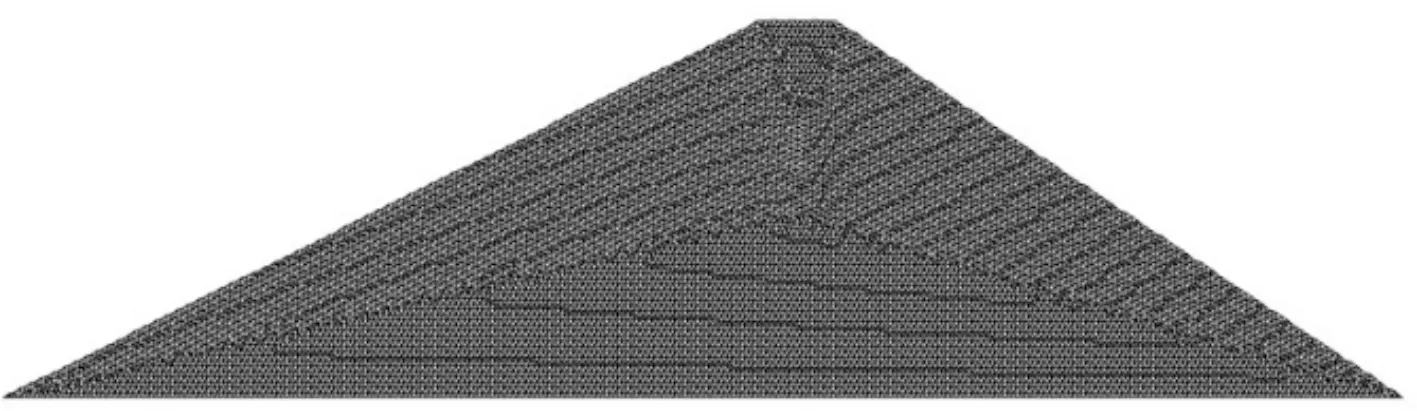
图3 验证模型网格(节点9 148个；单元17 795个)

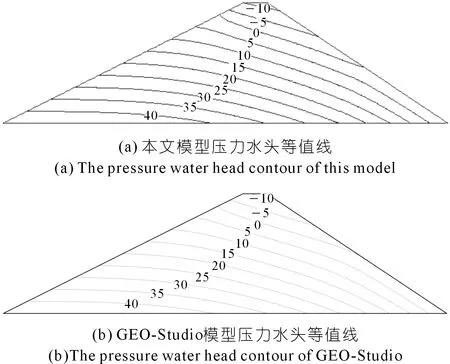
图4 验证算例压力水头等值线(单位：m)

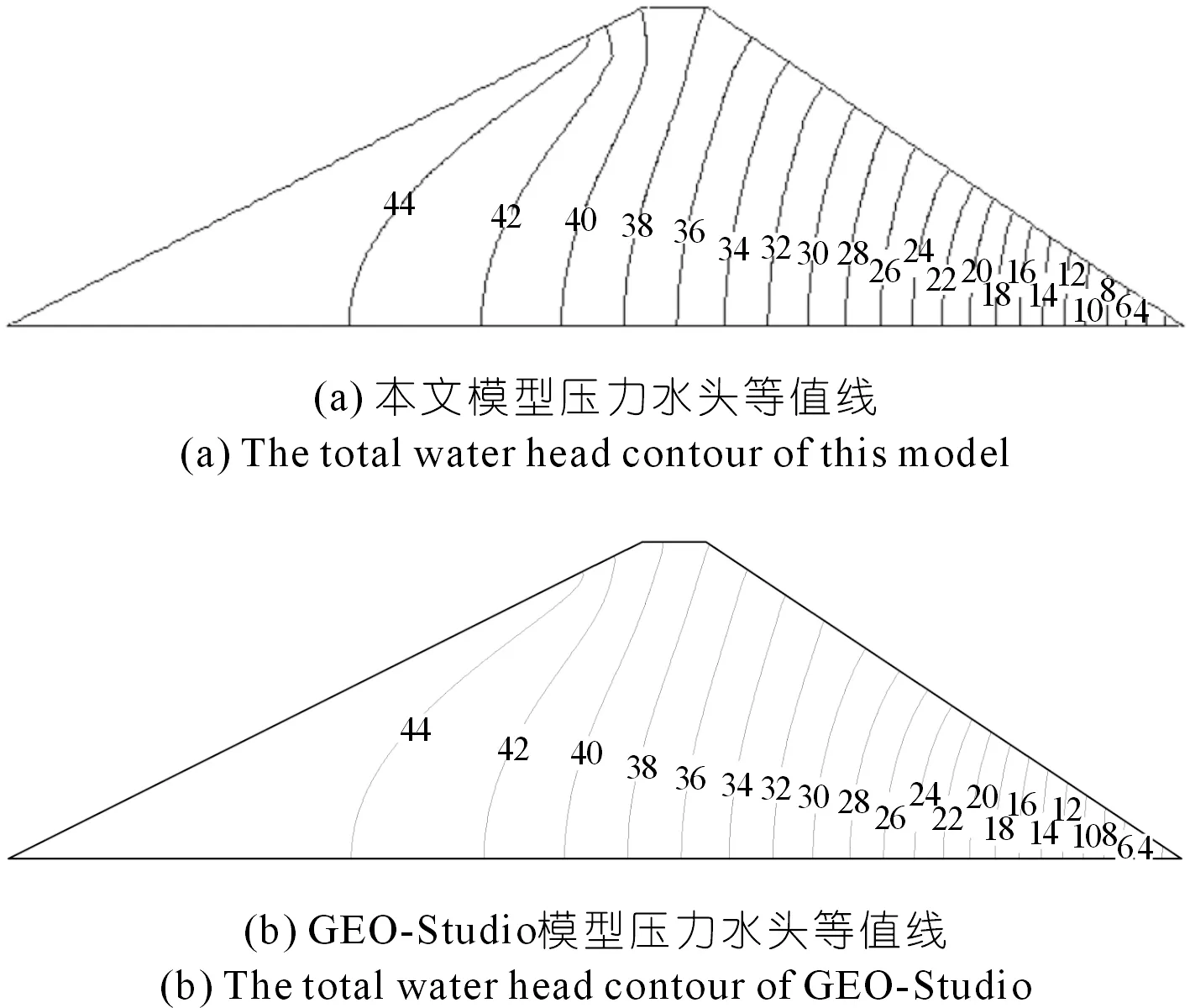
图5 验证算例总水头等值线(单位：m)

对比本文模型与GEO-Studio(2018学习版)结果，发现两者计算结果误差在±2.5%内，压力水头与总水头等值线的分布吻合，浸润线的位置接近，能满足工程计算需要。图6汇总了本文采用的各种计算方法及GEO-Studio的计算时间，通过对比时间结果发现，当采用预处理共轭梯度法(PCG)时，比只应用共轭梯度法(CG)速度提升了3.1倍，因为评估算例为均质坝，在一定程度上削减了预处理共轭梯度法的优势，当将其应用在非均质坝时，相信预处理共轭梯度法对于共轭梯度法的效率提升将会更加明显。当OpenACC与预处理共轭梯度法联合运用时，加速效果极为显著，加速比达到70，计算时间也远小于网格数量较多的GEO-Studio模型计算所需时间。

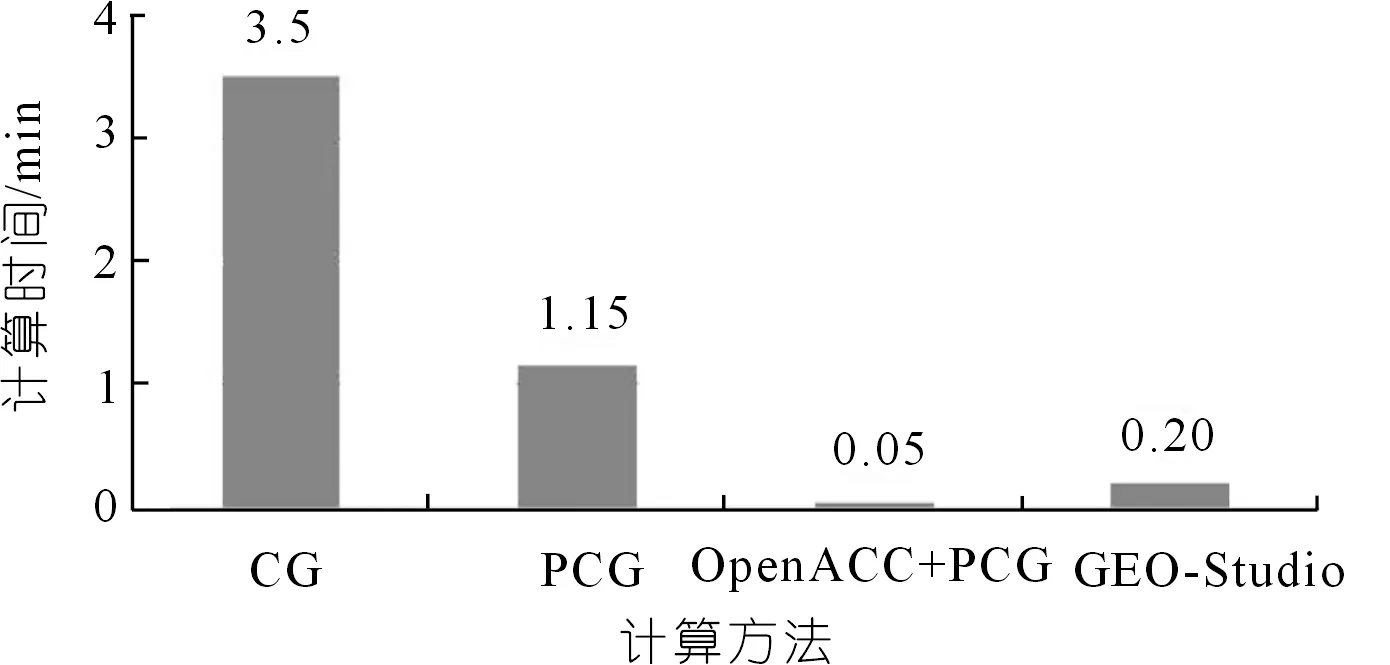
图6 不同计算方法的时间对比汇总

3 工程应用

甘肃省代古寺水库混凝土面板堆石坝位于大“S”形河道内，河谷狭窄，呈深切“V”字形，为横向或斜向河谷，两岸山体雄厚，岸坡高陡直立。河床底高程为1 667.00 m，正常蓄水位为1 804.00 m，下游尾水位为1 675.00 m，坝顶高程为1 809.00 m。表1为三维渗流计算的各材料分区渗透系数。图7为本模型采用的有限体积网格(节点725 036个；单元4 040 769个)，图8～9分别为大坝最大典型断面(坝0+115)的压力水头等值线与总水头等值线分布结果。由图可知，本文模拟结果与商业软件GEO-Studio结果具有较高一致性，验证了本文计算方法的正确性和可靠性。

表1 面板堆石坝各材料分区渗透系数

图7 应用算例有限体积网格

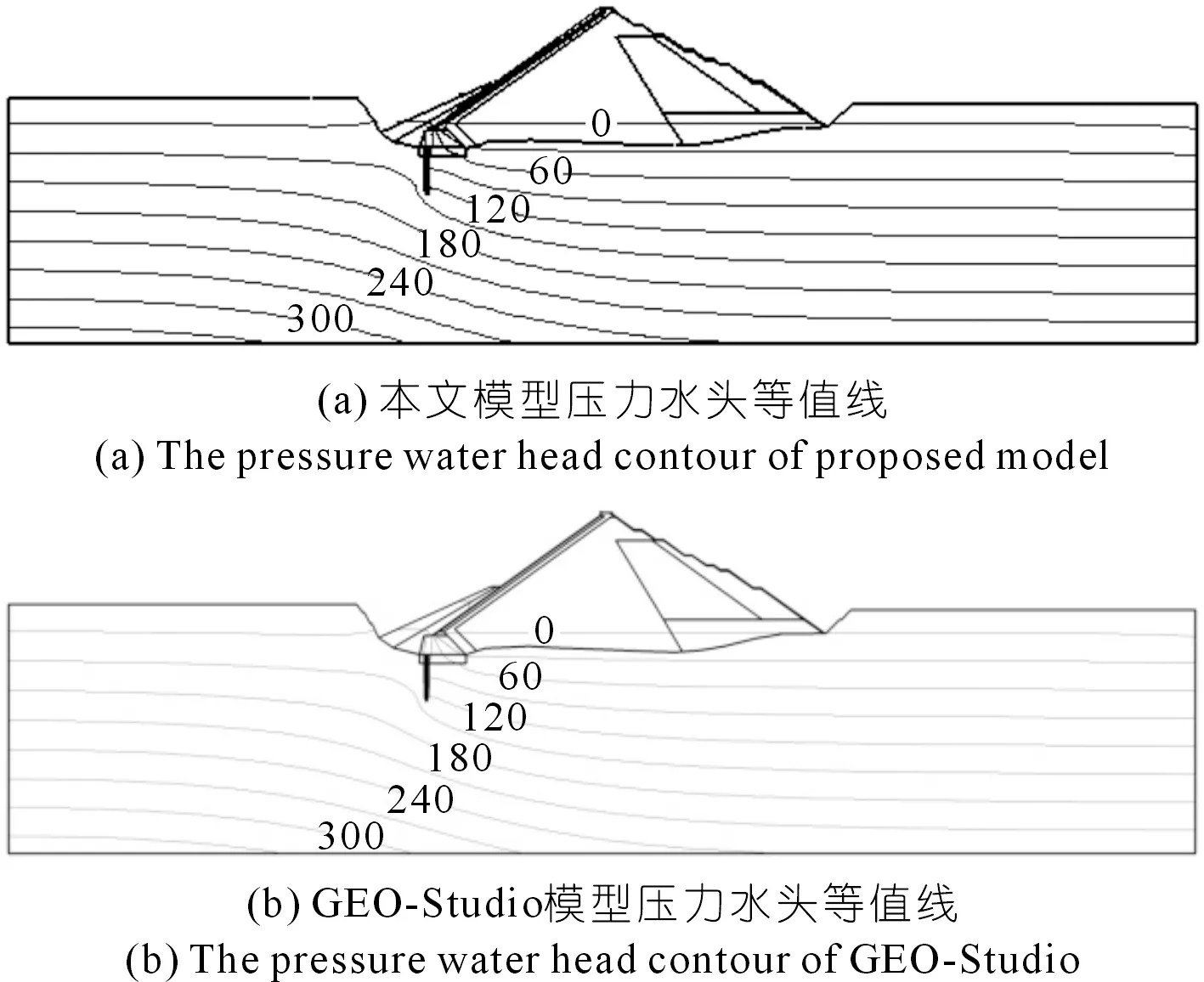
图8 工程应用算例最大典型断面(坝0+115)压力水头等值线(单位：m)

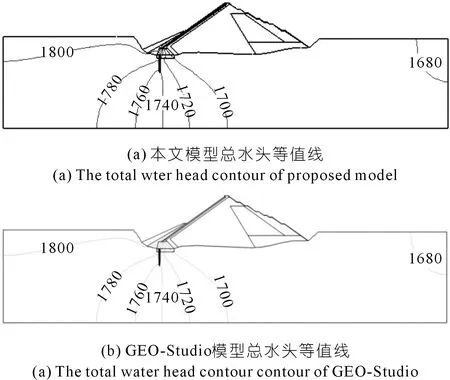
图9 工程应用算例最大典型断面(坝0+115)总水头等值线(单位：m)

4 结 语

本文提出了一种基于非结构化网格控制体积法渗流计算模型。模型采用预处理共轭梯度算法求解代数方程组，使用固定网格变渗透系数法求解域内含浸润面问题，发展了无系数矩阵数值迭代求解方法。验证算例与工程实际应用表明，本文所提出的土石坝三维稳态渗流计算方法有效可行，满足工程的实际需要。本文采用的OpenACC-GPU并行策略具有较高的加速比，为提高大型工程渗流计算效率提供了新的手段。