具有Cuntz半群消去律的C*-代数

范庆斋， 安璐

(上海海事大学文理学院，上海 201306)

0 引 言

ELLIOTT分类纲领指出，一类顺从的C*-代数可以按照K-理论、迹态空间及K-理论与迹态空间的配对(通常称为ELLIOTT不变量)进行分类。有许多重要的C*-代数类已经按照ELLIOTT不变量进行了分类，例如ELLIOTT等[1-2]对于单的有单位元的AH代数的分类。受到ELLIOTT等[1-2]关于单的AH代数分类的启发，LIN[3]提出迹拓扑秩不超过k的C*-代数，在这类C*-代数中，去掉了C*-代数的归纳极限结构，提出了一种新的C*-代数构造方法。这种新的结构，事实上就是由一类好C*-代数类通过迹逼近之后得到的C*-代数类。这种构造一方面去掉了归纳极限的结构，更容易验证某些C*-代数在这类C*-代数中，另一方面大大简化了分类定理中的唯一性定理。GONG等[4]对于单的顺从有单位元关于Jiang-Su代数稳定满足UTC条件的C*-代数给出了分类。事实上他们证明了这样的C*-代数是在一类称为广义迹拓扑秩不超过1的C*-代数张量上的一个UHF代数。

广义迹拓扑秩不超过1的C*-代数具有好的正则性质。正则性质在C*-代数分类中起关键的核心作用。正则性质一般是指关于Jiang-Su代数Z稳定、有限核维数、Cuntz半群的某些性质(例如Cuntz 半群的严格比较性质、可除性质等)。对于单的可分有单位元顺从的C*-代数，TOMS和WINTER猜想这3类正则性质等价。

ELLIOTT等[5]考虑了Ω类是满足某些性质的C*-代数，这些性质可以遗传到由Ω类中的C*-代数迹逼近之后得到的C*-代数类中。例如稳定秩一和投影的序由迹态决定等性质。并且这些性质对于某类C*-代数的分类起到关键性的作用。

FAN[6-7]考虑了Ω中某些K-群或者K-半群的性质可以遗传到由Ω类中的C*-代数迹逼近之后得到的C*-代数中。FAN[8]、ELLIOTT等[9]证明了Ω中某些正则性质可以遗传到由Ω类中的C*-代数迹逼近之后得到的C*-代数中。

RØRDAM等[10]提出Cuntz半群的弱消去律和投影的消去律，并证明了如果C*-代数是稳定秩一的，则它的Cuntz半群具有弱消去律和投影的消去律。

在本文中，设Ω是一类Cuntz半群具有弱消去律的C*-代数或者Cuntz半群具有投影消去律的C*-代数，证明了Cuntz半群的弱消去律性质或者Cuntz半群投影的消去律性质可以遗传到由Ω中的C*-代数迹逼近之后得到的C*-代数类TAΩ中。作为上述结论的应用：如果A是一个无限维有单位元单的Cuntz半群具有弱消去律性质的C*-代数(或者Cuntz半群具有投影消去律的C*-代数)，且设α:G→Aut(A)是有限群G作用在C*-代数A上并且作用具有迹Rokhlin性质，则交叉积C*-代数C*(G,A,α)的Cuntz半群具有弱消去律性质(或者Cuntz半群具有投影消去律)。

1 准备知识和定义

一个C*-代数A具有性质SP，是指对于A的任意非零可传C*-子代数，都包含一个非零投影。

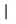
称a与bCuntz等价(记为a～b)，满足a⪯b并且b⪯a。记〈a〉为a的等价类。

〈a〉+〈b〉=〈a⊕b〉

序关系为

〈a〉≤〈b〉⟺a⪯b

设a和b是C*-代数A中的正元，记作[a]≤[b]，如果存在部分等距v∈A**使得对于任意的0≤c∈Her(A)，cv∈A，vv*=Pa，v*Her(a)v=Her(b)，其中Pa是a在A**中值域的投影(由[a]≤[b]可以得到aCuntz子等价于b，即a⪯b)。记[a]=[b]，满足v*Her(a)v=Her(b)。假设n是一个正整数，记n[a]≤[b]，则存在n个相互垂直的正元b1,b2,…,bn∈Her(b)满足[a]≤[bi]，i=1,2,…,n[11]。

设A是稳定有限的C*-代数，一个正元a∈A称为纯正元，满足a不Cuntz等价于一个投影。这等价于0不是a的谱σ(a)的聚点。

给定M∞(A)+中的正元a和ε>0，记(a-ε)+是由函数f(t)=max(t-ε,0),t∈σ(a)通过函数演算对应C*(a)中的元，由函数演算知道((a-ε1)+-ε2)+=(a-(ε1+ε2))+。

定理1.1A是一个有单位元稳定有限的C*-代数。

(1)设a,b∈A,任意的ε>0，如果||a-b||<ε，则存在A中一个压缩的元d使得(a-ε)+=dbd*。

(2)a是一个纯正元，对于任意的δ>0，任意的一个非负函数f∈C0(0,1]满足||f||=1，且在(δ/2,1)上f=0，在(0,δ/2)上f>0，则f(a)≠0，且(a-δ)++f(a)⪯a。

(3)下列等价：①a⪯b；②对于任意的ε>0，(a-ε)+⪯b；③对于任意的ε>0，存在δ>0，使得(a-ε)+⪯(b-δ)+。

(4)a和p是M∞(A)中的两个正元，其中p是一个投影，如果p⪯a，则存在M∞(A)中的元b使得p⊕b～a[12]。

定义1.1称C*-代数A的Cuntz半群W(A)，具有投影的消去律，是指对于M∞(A)+中任意的正元a、b，任意的投影p，由a⊕p⪯b⊕p可以得到a⪯b[10]。

定义1.2称C*-代数A的Cuntz半群W(A)具有弱消去律，是指对于M∞(A)+中的任意正元a、b、c和某个ε>0，由a⊕c⪯b⊕(c-ε)+，可以得到a⪯b[10]。

设Ω是一类C*-代数，则由Ω中的C*-代数迹逼近之后得到的C*-代数类记为TAΩ。

定义1.3一个有单位元单的C*-代数A属于TAΩ，是指对于任意的ε>0，任意的有限子集F⊆A，任意的a≥0，存在一个投影p∈A和A的C*-子代数B满足1B=p和B∈Ω，使得

(1)对于任意的x∈F，||xp-px||<ε。

(2)对于任意的x∈F，pxp∈εB。

(3)[1-p]≤[a][3，5]。

定理1.2如果Ω类对于张量上一个矩阵代数封闭，且对于有单位元的可传C*-子代数也是封闭的，则由Ω中的C*-代数迹逼近之后得到的C*-代数类TAΩ，对于张量上一个矩阵代数封闭，且对于有单位元的可传C*-子代数也是封闭的[3，5]。

下面的定理显然，略去证明。

定理1.3C*-代数Cuntz半群的投影消去律和弱消去律可以遗传到张量上一个矩阵代数和有单位元的可传的C*-子代数中。

定义1.4A是一个无限维的可分的有单位元单的C*-代数，设α:G→Aut(A)是一个有限群G作用在C*-代数A上。称α具有迹Rokhlin性质，是指对于任意的有限子集F⊆A和任意的ε>0，任意的非零正元b∈A和任意的g∈G，存在相互垂直的投影eg∈A满足

(1)对于任意的g,h∈G，||αg(eh)-egh||<ε。

(2)对于任意的d∈F，g∈G，||egd-deg||<ε。

(3)记e=∑g∈Geg，则投影1-e⪯b。

(4)||ebe||≥||b||-ε[13]。

2 主要结果

定理2.1设Ω是一类稳定有限有单位元C*-代数，如果对于任意的B∈Ω，且B的Cuntz半群W(B)具有投影的消去律，则对于任意有单位元单C*-代数A∈TAΩ，A的Cuntz半群W(A)具有投影的消去律。

证明:设a和b是正元，p是投影，都在M∞(A)+中，满足a⊕p⪯b⊕p，只要证明对于任意的ε>0，(a-3ε)+⪯b即可。

由定理1.1知，存在v∈A和δ′>0，满足

v(diag((p-δ′)+b))v*=p+a

对于F={a,b,p,d,d*}，任意的δ>0，由于A∈TAΩ，存在A的C*-子代数B和非零投影q∈A，满足B∈Ω和1B=q，使得

(1)对于任意的x∈F，||xq-qx||<δ。

(2)对于任意的x∈F，qxq∈δB。

由此可知，存在正元a′,b′,d′,d′*∈B，投影p′∈B，正元a″,b″,d″,d″*∈(1-q)A(1-q)和投影p″∈(1-q)A(1-q)，使得||a-a′-a″||<2δ，||b-b′-b″||<2δ，||a′+p′+a″+p″-(d″+d′)(b′+p′+b″+p″)(d′*+d″*)||<4δ。

因此可得到

||a′+p′-d′(b′+p′)d′*||<4δ

||a″+p″-d″(b″+p″)d″*||<4δ

由定理1.1得

(a′+p′-4δ)+⪯b′+p′

(a″+p″-4δ)+⪯b″+p″

因为a′,p′,b′,(a′-4δ)+∈B，并且B∈Ω，所以(a′-4δ)+⪯b′。

③[1-q-r]≤[(a′-4δ)+]。

由①和②可知，存在正元a‴,b‴,e‴∈D，投影p‴∈D，正元a″″,b″″,e″″∈(1-q-r)A(1-q-r)和投影p″″∈(1-q-r)A(1-q-r)，使得

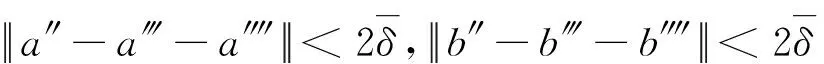
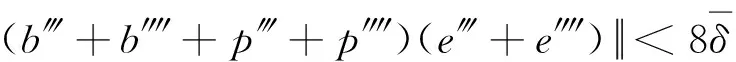
因此

从而有

(a-3ε)+⪯(a′-ε)++(a″-ε)+⪯

[p″″]+[c]+(a‴-ε/3)++(a″″-ε/3)+⪯

[p″″]+[c]+b‴+(a″″-ε/3)+⪯

因为ε>0是任意的，所以a⪯b。

定理2.2设Ω是一类有单位元的C*-代数，Ω对于有单位元可传C*-子代数和张量上一个矩阵代数是封闭的。A∈TAΩ是一个无限维的单的有单位元的C*-代数，设α:G→Aut(A)是有限群G作用在一个C*-代数A上，并且作用具有迹Rokhlin性质，则交叉积代数C*(G,A,α)在TAΩ中[14]。

推论2.1设A是一个稳定有限无限维有单位元单的C*-代数，A的Cuntz半群W(A)具有投影的消去律。设α:G→Aut(A)是有限群G作用在C*-代数A上，并且作用具有迹Rokhlin性质，则交叉积C*-代数C*(G,A,α)的Cuntz半群也具有投影的消去律。

定理2.3设Ω是稳定有限有单位元的C*-代数类，并且对于任意的B∈Ω，B的Cuntz半群W(B)具有弱消去律，则对于任意有单位元单C*-代数A∈TAΩ，A的Cuntz半群W(A)也具有弱消去律。

证明：设a、b、c是M∞(A)+中的正元，满足a⊕c⪯b⊕(c-δ)+，其中δ>0，则对于任意的ε>0，只要证明(a-3ε)+⪯b即可。

由定理1.2和定理1.3，不失一般性，假设a、b、c都在A中，并且ac=bc=0。不妨假设c是一个纯正元，否则cCuntz等价于一个投影，由定理2.1和对于任意的δ>0，(p-δ)+=p，可以得到结论。

由于c是一个纯正元，由定理1.1，存在正元g∈A，对于任意的δ″>0，使得

由定理1.1，存在v∈A和δ′>0，使得

由定理1.1，存在一个压缩元d∈A，使得

对于F={a,b,c,g,d,d*}，任意的η>0，由于A∈TAΩ，存在A的C*-子代数B和非零的投影q∈A，满足B∈Ω和1B=q，使得

(1)对于任意的x∈F，||xq-qx||<η。

(2)对于任意的x∈F，qxq∈ηB。

由此可知，存在正元a′,b′,g′,c′,d′,d′*∈B，正元a″,b″,c″,g″,d″,d″*∈(1-q)A(1-q)，使得

||a-a′-a″||<2η

||b-b′-b″||<2η

(c″-δ)+(d′*+d″*)||<6η

因此可以得到

d′(b′+(c′-δ)+)d′*||<6η

d″(b″+(c″-δ)+)d″*||<6η

由定理1.1知

a′+(g′-δ′-2δ″-6η)++c′⪯b′+(c′-δ)+

由于a′,c′,b′∈B，并且B∈Ω，可以得到a′+(g′-2δ′-δ″-6η)+⪯b′。

同样的道理，存在e″∈(1-q)A(1-q)和δ‴>0，使得

a″+g″+(c″-2δ′-δ″-2δ‴-6η)+=

e″(b″+(c″-δ)+)e″*

③[1-q-r]≤[(g′-2δ′-δ″-6η)+]。

由此可知，存在正元a‴,c‴,b‴∈D和正元a″″,c″″,b″″∈(1-q-r)A(1-q-r)，使得

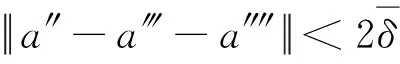
取δ′,δ″,δ‴,η，使得

||a‴+g‴+(c‴-2δ′-δ″-2δ‴-6η)++a″″+g″″+

(c″″-2δ′-δ″-2δ‴-6η)+-(e‴+e″″)(b‴+

b″″+(c‴-δ)++(c″″-δ)+)(e‴+e″″)||<6δ

最后得到

||a‴+g‴+(c‴-2δ′-δ″-2δ‴-6η)+-

||a″″+g″″+(c″″-2δ′-δ″-2δ‴-6η)+-

由定理1.1知

b‴+(c‴-δ)+

b″″+(c″″-δ)+)

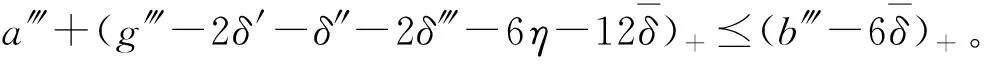
(a-3ε)+⪯(a′-ε)++(a″-ε)+⪯

(g′-2δ′-δ″-6η)++(a′-ε)++(a‴-ε/3)+⪯

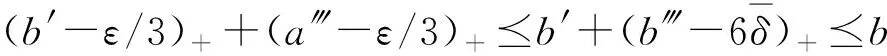
因为ε>0是任意的，所以可以得到a⪯b。

推论2.2设A是一个无限维有单位元单的C*-代数，A的Cuntz半群W(A)具有弱消去律。设α:G→Aut(A)是有限群G作用在C*-代数A上，且作用具有迹Rokhlin性质，则交叉积C*-代数C*(G,A,α)的Cuntz半群具有弱消去律。

3 结 论

本文得到了如下的结论：(1)设Ω是一类Cuntz半群具有弱消去律的C*-代数。证明了Cuntz半群的弱消去律可以遗传到由Ω中的C*-代数迹逼近之后得到的C*-代数类TAΩ中。(2)设Ω是一类Cuntz半群具有投影消去律的C*-代数。证明了Cuntz半群的投影消去律可以遗传到由Ω中的C*-代数迹逼近之后得到的C*-代数类TAΩ中。

作为上述结论的应用得到了如下结果：(1)如果A是一个无限维有单位元单的Cuntz半群具有弱消去律性质的C*-代数，且设α:G→Aut(A)是有限群G作用在C*-代数A上并且作用具有迹Rokhlin性质，则交叉积C*-代数C*(G,A,α)的Cuntz半群具有弱消去律。(2)如果A是一个无限维有单位元单的Cuntz半群具有投影消去律的C*-代数，且设α:G→Aut(A)是有限群G作用在C*-代数A上并且作用具有迹Rokhlin性质，则交叉积C*-代数C*(G,A,α)的Cuntz半群具有投影消去律。