复合潮汐信息的感潮河段船舶交通流滚动预测模型

齐绪存， 黄常海， 沈佳， 娄乃元

(上海海事大学商船学院， 上海 201306)

0 引 言

随着中国社会经济的快速发展，特别是对外贸易的快速发展，水上交通运输发展迅速，船舶交通流量不断增加，导致特定河段内通航效率下降[1]，特别是感潮河段在高峰时刻交通拥堵现象比较明显。

感潮河段是连通内河航道、港口与沿海航道的重要通道，感潮河段的水位和水流受潮汐影响明显。在感潮河段，吃水较大的船舶需要乘潮进出港；出于节省燃料的目的，大批小型船舶也乘潮航行。因此，感潮河段交通流潮汐效应比较明显。对感潮河段交通流的精准预测，可为海事管理机构交通管理措施调整、引航机构引航计划制定和船舶航次计划制定等提供决策参考，缓解感潮河段交通拥堵问题，进一步提高感潮河段通航效率。

目前，针对船舶交通流特性，学者们提出了多种预测模型：考虑非线性、复杂性等特性的二维矩阵分解预测模型[2]；考虑出发港口、周转港口、目的港口间时空关联性的预测模型[3]；考虑季节和气候等因素的适用于周期波动船舶交通流的预测模型[4]；考虑船舶交通流随机性、非线性特点的基于机器学习算法的预测模型[5-8]；等等。然而，上述预测模型多考虑船舶交通流自身特性，未充分考虑感潮河段潮汐波动对船舶交通流的影响，存在一定的预测误差。

为充分利用潮汐波动对船舶交通流量的影响，本研究提出复合潮汐信息的船舶交通流预测方法。综合利用潮汐信息和历史交通流信息，需选择多变量预测模型。常见的多变量预测模型有1阶N变量灰色预测模型GM(1,N)、智能算法模型(支持向量机、神经网络等)等。GM(1,N)可在小样本、贫信息情况下保持较高的预测精度，已被运用于多个领域[9-11]。在GM(1,N)基础上，MA等[12]将GM(1,N)灰色差分式右端项中的齐次项函数转为非线性核函数，提出KGM(1,N)，预测精度得到进一步提升。考虑船舶交通流非线性等特性，选择KGM(1,N)作为本研究基础模型。然而，KGM(1,N)灰色差分式中背景值存在预估误差。本研究选用插值系数法[13]对KGM(1,N)进行背景值优化，构建基于背景值优化的KGM(1,N)(KGM(1,N) based on background value optimization, KGBM(1,N))模型。KGBM(1,N)模型存在最优参数确定问题，即高斯核参数σ、修正参数C和背景值插值系数λ的确定。考虑到粒子群优化(particle swarm optimization, PSO)算法具有原理简单、容易实现、全局搜素能力强、运算速度快等优点[14]，选择PSO算法确定本研究模型所需最优σ、C和λ，构建基于PSO算法优化的KGBM(1,N)(the KGBM(1,N) model based on PSO, PSO-KGBM(1,N))模型，并采用实时滚动预测方法。为验证PSO-KGBM(1,N)滚动预测模型在感潮河段的适用性，以上海港南槽航道九段警戒区上游断面的船舶交通流预测为例进行应用，与常见预测模型对比验证其预测精度。

1 复合潮汐信息的船舶交通流预测方法

感潮河段船舶交通流量增减趋势与该河段潮汐波动具有较强的相关性。一般情况下，感潮河段潮汐波动与船舶交通流之间存在一定的时间差T，即存在船舶交通流变化相较潮汐波动滞后或超前一段时间的情况。为此，感潮河段船舶交通流预测模型应将感潮河段潮汐信息和历史交通流信息同时作为预测模型的输入信息，即输入时段T+1至T+m的船舶交通流量数据和时段1至m的潮高数据，这些数据形成m×2维矩阵：

(1)

式中：Z1表示时段T+1至T+m的船舶交通流量数据；Z2表示时段1至m的潮高数据。

预测任意时段船舶交通流量的模型可用下式表示：

(2)

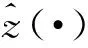
(3)

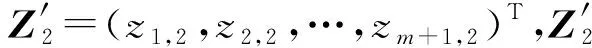
2 模型机理

2.1 KGBM(1,N)模型构建

(i=1,2,…,N;k=2,3,…,m)

(4)

KGBM(1,N)模型的灰色差分式为

(5)

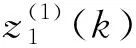
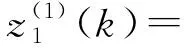
(k=2,3,…,m;λ∈[0,1])

(6)

可通过调节背景值系数λ的值，确定最优背景值。当λ=0.5时，式(6)为传统背景值定义式，即梯形公式求解下的背景值，此时式(5)为KGM(1,N)模型的灰色差分式。

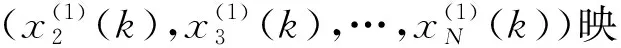
φ(k)=wT·φ(χ(k))

(7)

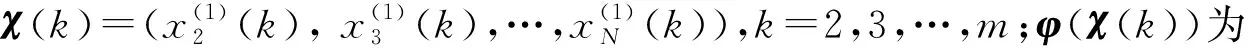
由于式(5)中φ(χ(k))不可通过式(7)给定，故不可直接用最小二乘法求解式(5)中的φ(k)、a、u的值，上述问题需转化为正则化问题：

(8)

式中：C为修正参数；ek为预设误差。

采用拉格朗日乘子法引入拉格朗日乘子βk(k=2,3,…,m)求解后，通过KKT(Karush-Kuhn-Tucker)条件式将上述问题转化为线性求解问题[12]，即

(9)

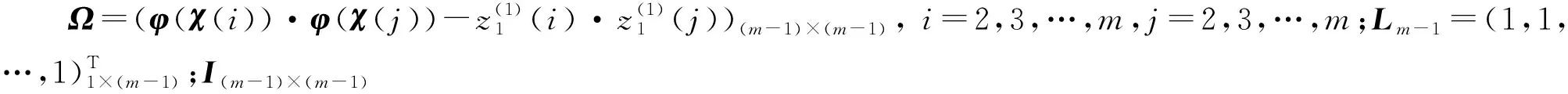
本研究采用高斯核给定内积φ(χ(i))·φ(χ(j))的值，即

K(χ(i),χ(j))=φ(χ(i))·φ(χ(j))=

(10)

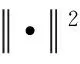
φ(k)=wT·φ(χ(k))=

结合式(5)与式(6)，有

φ(k)+u,k=2,3,…,m

(11)

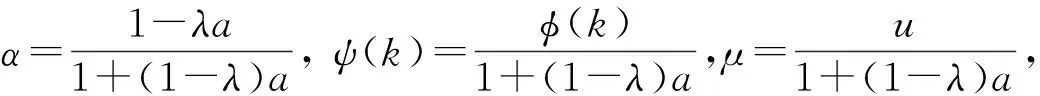
k=2,3,…,m

(12)

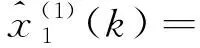
k=2,3,…,m

(13)

通过一阶累减得到原始序列的预测值：

k=2,3,…,m

(14)

2.2 PSO-KGBM(1,N)模型最优参数确定

s.t.

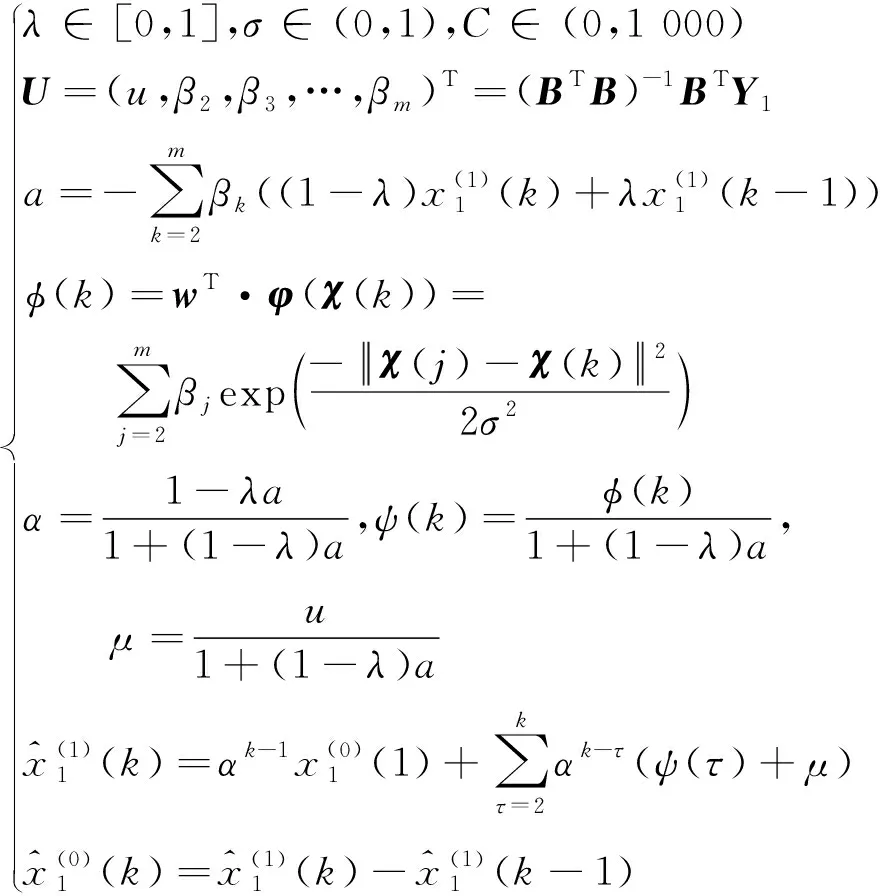
(15)

PSO算法的速度和位置迭代公式分别如下：

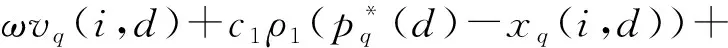
(16)

xq+1(i,d)=xq(i,d)+vq+1(i,d)

(17)

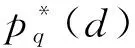
x1(i,d)=Pmin(d)+r(Pmax(d)-Pmin(d))

(18)

式中：r为[0,1]内的随机数；Pmin(d)和Pmax(d)分别为第d个参数取值范围的下限和上限，在本研究中为λ、σ和C的取值范围下限和上限。

本研究初始定义了50组关于λ、σ和C的初始值，迭代次数为300次。具体的算法步骤如算法1所示：

算法1

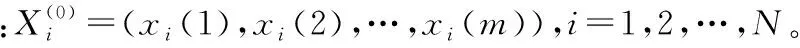
1.初始状态下自定义系数ω=0.8，c1=2，c2=2，确定最大迭代次数为300。

2.分别在[0,1]内随机选取50个粒子λ1(i)，在(0,1)内随机选取50个粒子σ1(i)，在(0,1 000)内随机选取50个粒子C1(i)，并确定这些粒子的初始个体最优解为随机取值。

3.Forq=1:300

(1)Fori=1:50

①将经q次迭代给定的λq(i)、σq(i)、Cq(i)代入式(5)～(11)确定式(13)内所需参数的值。

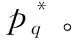
(2)End for

(4)通过式(16)和式(17)更新经q+1次迭代后得到的λq+1(i)、σq+1(i)、Cq+1(i)的初始位置。

4.End for

输出：最终的全局最优解即为λ、σ和C的最优取值。

2.3 PSO-KGBM(1,N)滚动预测模型预测步骤

确定拟合序列长度n和预测序列长度p，n应保持大于p。在确定n和p后，用PSO-KGBM(1,N)滚动预测模型进行预测，步骤如下：

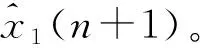
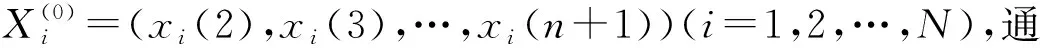
步骤4重复循环步骤3，直至完成所有待测点预测。

PSO-KGBM(1,N)滚动预测模型的预测流程见图1。

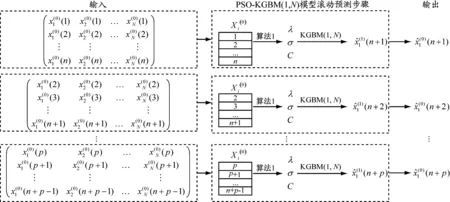
图1 PSO-KGBM(1,N)滚动预测模型的预测步骤

3 数值案例

实验数据来源于上海港南槽航道九段警戒区上游断面(以下简称“实验断面”)的AIS和雷达跟踪数据。该航道船舶交通流存在明显波动规律，且与该航道潮汐波动规律具有一定相似性。选取实验断面2020年5月22日和23日的小时进口船舶交通流量数据，验证本研究所提出模型的精度。为验证复合潮汐信息对模型预测的影响，选择1阶单变量的非线性核函数灰色预测模型KGM(1,1)作为比较模型；为验证船舶交通流非线性特性对模型预测的影响，选择离散1阶N变量灰色模型DGM(1,N)作为比较模型；为验证灰色模型在小样本情况下的优势，将传统智能算法模型(最小二乘支持向量机(least square support vector machine, LSSVM)模型、反向传播(back propagation, BP)神经网络模型)作为比较模型。

利用相关系数法[16]分别对实验断面5月22日和23日全天船舶交通流量数据与该地区前置1～12 h潮汐的潮高数据进行相关性分析，计算所得的相关系数见表1。由表1可知，5月22日和23日全天船舶交通流量数据均与其前置8 h潮高数据的相关系数最高，接近0.9。船舶交通流量与前置8 h潮高变化趋势见图2和3。

由图2和3可知，实验断面5月22日和23日的小时进口船舶交通流量与该地区前置8 h的潮高数据的波动变化趋势具有较高相似性。根据第1节提出的复合潮汐信息的船舶交通流量预测方法，可将该组船舶交通流量数据作为本研究模型实验数据，各时段船舶交通流量数据及前置8 h潮高值见表2。

表1 2020年5月22日和23日00:00—24:00船舶交通流量与地区前置1～12 h的潮高数据间的相关系数

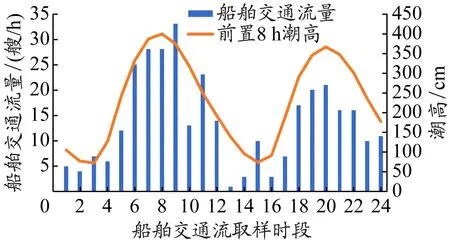
图2 2020年5月22日船舶交通流量与前置8 h潮高关系

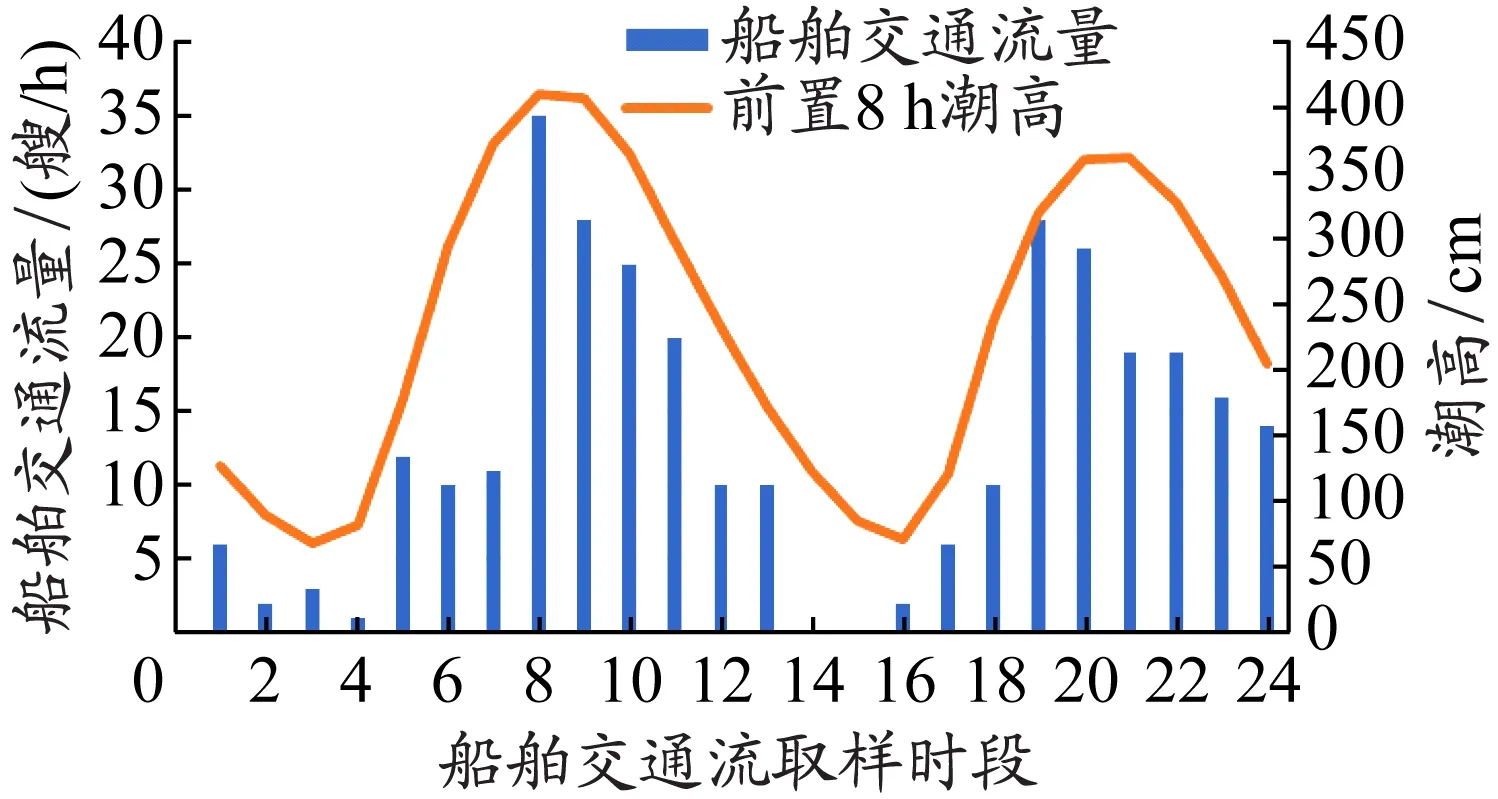
图3 2020年5月23日船舶交通流量与前置8 h潮高关系

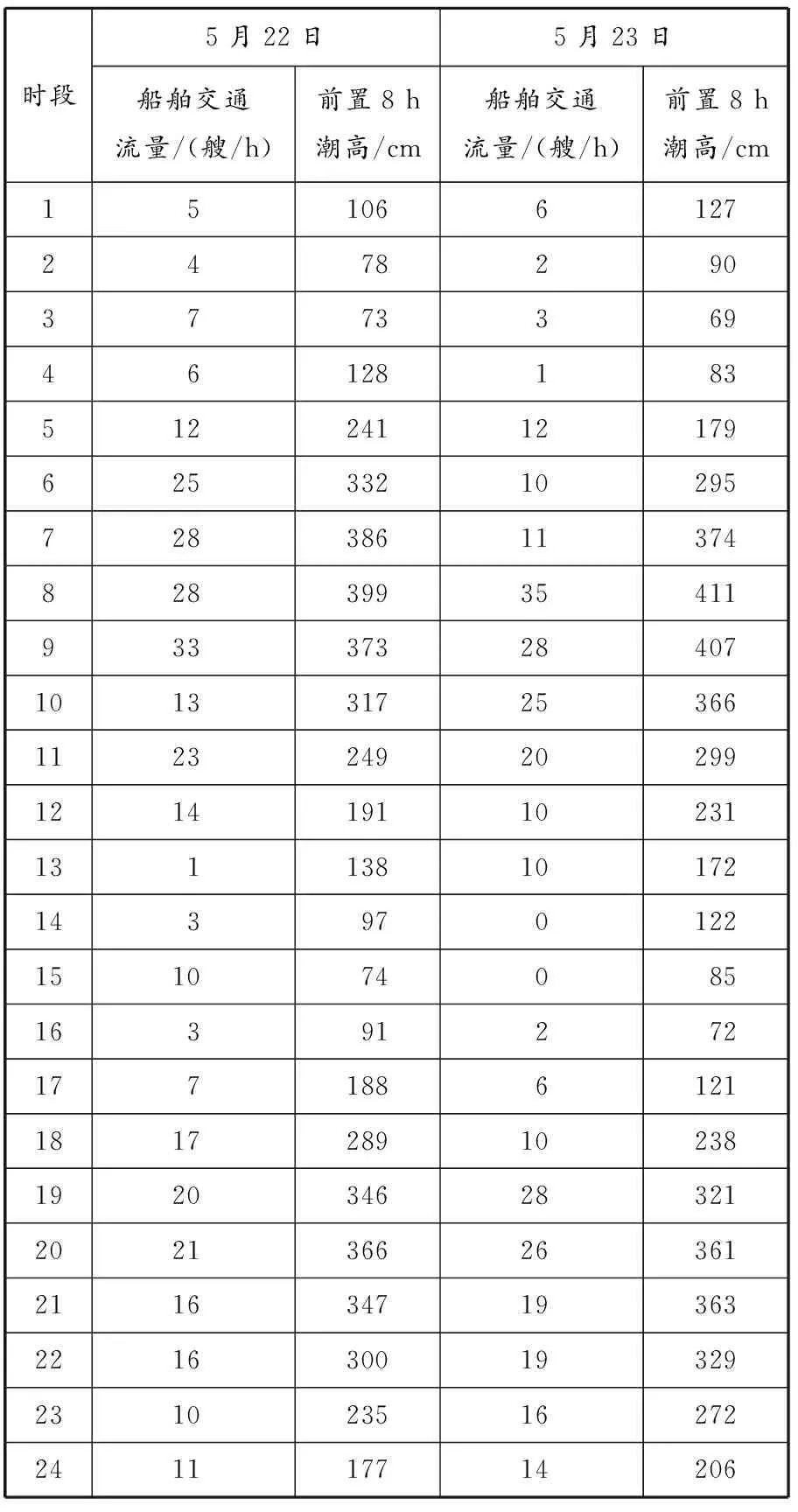
表2 2020年5月22日和23日船舶交通流量及前置8 h潮高

3.1 评价指标

为评价预测结果，采取最大绝对误差EMA、平均绝对百分比误差EMAP和等值系数CE反映模型的预测精度。

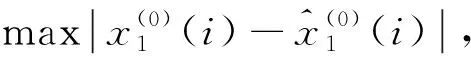
i=1,2,…,m

EMA和EMAP值越小，说明模型预测精度越高；CE值越大，说明模型预测精度越高。

3.2 最优预测时间窗与输入矩阵确定

通过相关系数法得到2020年5月22日和23日船舶交通流量数据与前置8 h潮高数据的相关系数最高，因此，为保持较高精度，利用复合潮汐信息预测未来时刻船舶交通流的预测时间窗宽度(预测序列长度)应小于等于8，即时间窗宽度的取值范围为[1,8]h。为确定最优时间窗宽度，计算不同宽度的时间窗内的EMAP值。

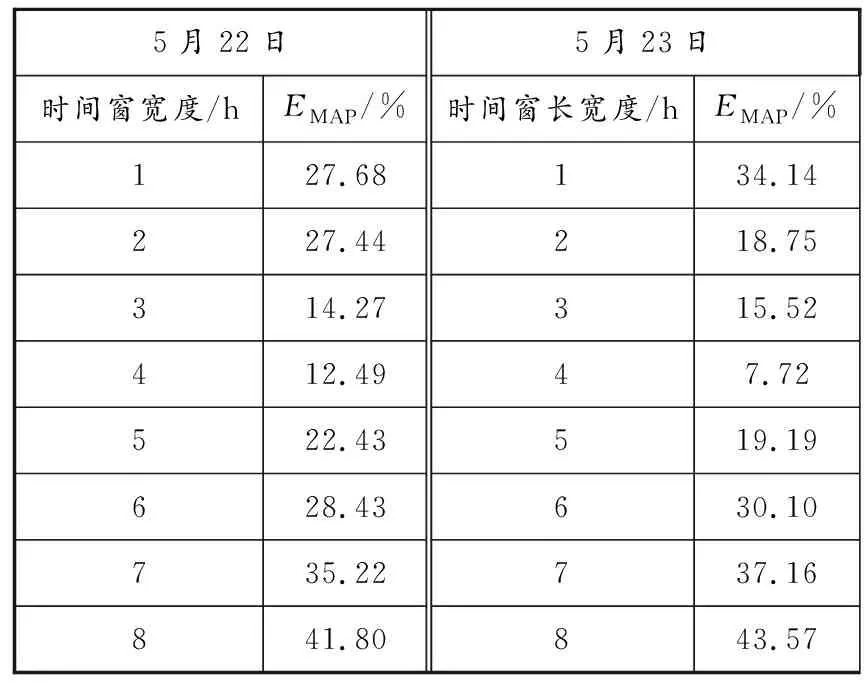
表3 2020年5月22日和23日不同宽度的时间窗内的预测精度比较

通过表3中不同宽度时间窗内的预测精度结果，可知时间窗宽度为4 h(拟合序列长度设定为20，预测序列长度设定为4)时的EMAP值最低。因此，本实验案例将预测序列长度设定为4，将拟合序列长度设定为20，以00:00—20:00(时段1～20)的船舶交通流量数据作为拟合数据，20:00—24:00的船舶交通流量数据作为验证数据。

确定好预测序列长度和拟合序列长度后，以5月23日20:00—24:00的船舶交通流量预测为例，具体的输入矩阵及预测过程如下：

3.3 预测结果

本研究模型与DGM(1,N)模型、LSSVM模型和BP神经网络模型均利用感潮河段内复合潮汐信息。KGM(1,1)模型虽未利用复合潮汐信息，但其右端项采用核函数替代齐次项函数或常数，与本研究模型一致。模型预测结果见图4和5，预测精度比较见表4和5。

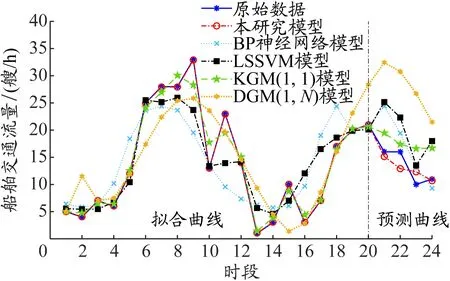
图4 船舶交通流量预测结果(2020年5月22日)

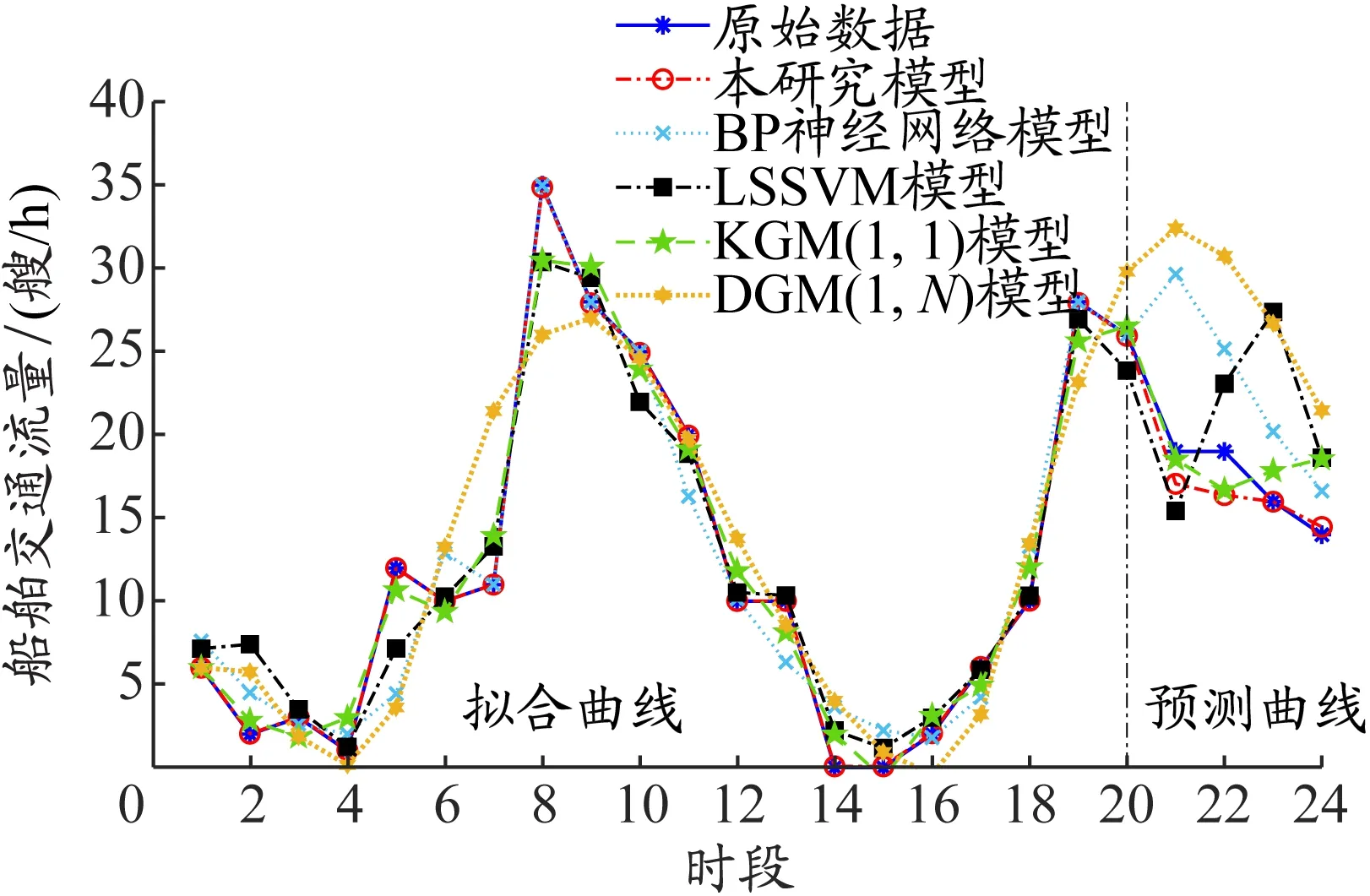
图5 船舶交通流量预测结果(2020年5月23日)

通过图4与图5可明显看出，本研究模型在拟合过程中优于其他模型，几乎与原始数据曲线重叠。DGM(1,N)模型无论是拟合还是预测曲线均是几种模型中与原始数据曲线偏差最大的，且比较平滑，这是由于DGM(1,N)模型相较其他模型并不能有效反映船舶交通流的非线性和随机性等特性。

由表4和5对连续两天船舶交通流预测精度的比较结果可知，本研究模型在EMAP、EMA、CE指标上均明显优于其他几种对比模型。本研究模型预测结果的EMA值均在3.1以下，而在其他4种模型中，预测较好的KGM(1,1)模型和BP神经网络模型的EMA值分别超过了4.5和8，预测精度最差的DGM(1,N)模型的EMA值超过了13。此外，本研究模型CE值均在0.92以上，EMAP值均小于13%，其他4组模型的预测精度与本研究模型的预测精度具有一定差距。

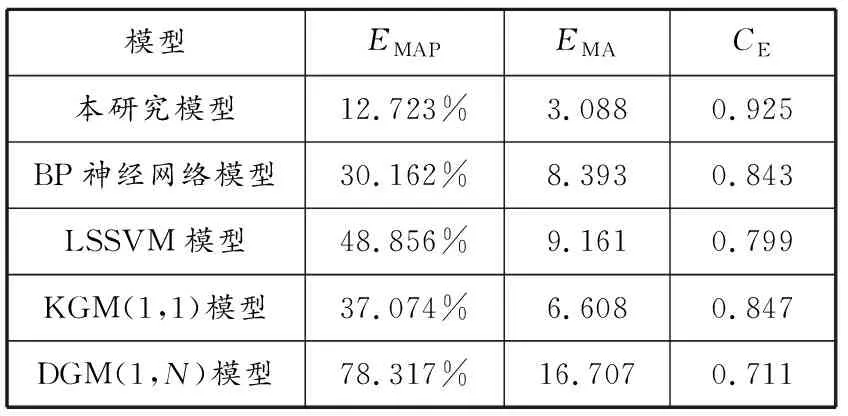
表4 船舶交通流量预测精度比较(2020年5月22日)

表5 船舶交通流量预测精度比较(2020年5月23日)

4 结 论

充分考虑潮汐对船舶交通流量的影响和船舶交通流非线性等特性，提出复合潮汐信息的船舶交通流预测方法。提出一种适用于感潮河段船舶交通流预测问题的复合潮汐信息的PSO-KGBM(1,N)滚动预测模型，并以上海港南槽航道九段警戒区上游断面船舶交通流预测为例进行验证。经与智能算法模型(LSSVM模型、BP神经网络模型)、DGM(1,N)模型、KGM(1,1)模型进行系统科学的比较，发现所提出的PSO-KGBM(1,N)滚动预测模型预测精度明显优于其他对比预测模型。

(1)本研究模型选取KGM(1,N)模型作为基础模型，模型的右端项为可选择的非线性核函数，可更好地反映潮汐对船舶交通流的影响。

(2)本研究提出的PSO-KGBM(1,N)滚动预测模型采用插值系数法优化背景值，并采用PSO算法确定背景值系数λ、右端项核函数所需高斯核参数σ和修正参数C的最优取值，预测精度较高。

(3)采用实时滚动预测方法，可在数据有限的条件下保持新信息优先，从而模型精度更高，工程应用难度更低。

感潮河段上游水库放水或极端天气带来的航道水位突变对船舶交通流预测的影响，有待进一步研究。