有弱局部单位半群的内射系

梁星亮乔彦赫 陈晓洁

(1.陕西科技大学数学学院,陕西西安 710021;2.西北大学数学学院,陕西 西安 710127;3.陕西科技大学设艺学院,陕西西安 710021)

1 引言

本文中S表示半群.称半群S有弱左局部单位,如果对任意的s∈S,存在u∈S使得us=s.称半群S有共同弱左局部单位,如果对任意的s,t∈S,存在u∈S使得us=s且ut=t.显然,群、幺半群和右零半群都是有(共同)弱左局部单位的半群.同样的方式可以定义有(共同)弱右局部单位的半群.

设S是半群(未必含有幺元),A是非空集合.若有映射f:S×A→A,(s,a),满足

则称A是左S-系,或称S左作用于A上,简记SA或者A.特别地,当S是幺半群(1为其幺元)时,如果映射f在条件(1)基础上又满足

则称A是单式左S-系.设A,B都是左S-系.称映射g:A→B为从A到B的左S-同态,如果g(sa)=sg(a),∀s∈S,∀a∈A.所有左S-系以及左S-系之间的S-同态构成一个范畴,称为左S-系范畴.在左S-系范畴中,直积和余直积具有非常简单的表达:它们分别是卡式积和不交并.

设S是半群.称左S-系A是酉S-系,如果SA=A.若S是有弱左局部单位半群,则对每一个a∈A,存在u∈S使得a=ua.所有的酉左S-系和它们之间的S-系同态构成左S-系范畴的一个全子范畴,称为酉左S-系范畴.

设λ是左S-系A上的等价关系.若λ满足 (a,b)∈λ=(sa,sb)∈λ,∀s∈S,∀a,b∈A,则称λ为A上的左S-同余.在A关于同余λ的商集A/λ上定义左S-作用s(aλ)=(saλ),∀s∈S,∀a∈A,则容易验证A/λ关于上述左S-作用构成一个S-系,称为A关于λ的商系.对任意的a∈A,a所在的等价类记为[a]λ.

设S是半群,E是S-系.称E是内射的[1],如果对任意S-单同态f:A→B和任意S-同态g:A→E,存在S-同态h:B→E,使得下图可换:

众所周知,半群代数理论在自动机理论、计算机科学和代数表示论等方面都有广泛的应用[2-5].而半群的S-系理论作为半群的一种表示理论,是研究半群的有力工具[6-7].内射系作为S-系理论中重要的系类,是半群同调分类的主要研究对象之一.文献[1]率先在半群的S-系范畴中引入了内射系的概念,证明了幺半群的S-系范畴具有足够内射对象,并研究了幺半群S-系的内射包络.与环模理论不同的是,在幺半群的S-系理论中弱内射系不一定是内射的[4].受文献[1]的启发,许多学者开始致力于S-系内射包络以及内射系推广的研究,目前已有大量系统的和深刻的成果面世[8-15].有弱局部单位半群的概念在文献[13]中首次提出.本文试图将幺半群上S-系的内射理论推广至有弱局部单位半群上.利用S-系同态的可收缩性给出了内射S-系的等价刻画,证明了有共同弱左局部单位半群的S-系都可嵌入到一个内射系中,通过建立S-系的内射性与其方程组的可解性之间的联系,给出了所有S-系是内射的有弱左局部单位半群的特征,推广了幺半群理论中相应的结果.

本文未定义的术语及记法参见文献[4,6].下文除特殊声明以外,所考虑的S-系均是酉左S-系.

2 基本性质

本节主要研究半群的内射S-系的基本性质.通过建立S-系的内射性质与可收缩单同态之间的联系,给出内射系的等价刻画,以及内射系与直积的关系.

为了刻画内射S-系,需要S-单同态是可收缩的概念.设f:A→B是S-单同态.称f是可收缩的,如果存在S-同态g:B→A使得gf=1A.利用内射系的定义容易验证.

命题 2.1设S是半群,若S-单同态f:E→G是可收缩的,且G是内射系,则E也是内射系.

下面构造一个内射S-系的重要例子.对任意S-系A引进下述记号:

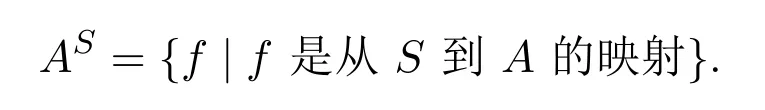
如下规定S在AS上的左作用:(sf)(x)=f(xs),∀f∈AS,∀s,x∈S.显然,sf∈AS.因为对任意s,t,x∈S,有 (t(sf))(x)=(sf)(xt)=f(xts)=((ts)f)(x),所以AS是左S-系.

命题 2.2设S是有弱左局部单位半群,则对于任意S-系A,AS是内射S-系.

证明设ϕ:B→C是任意S-单同态,g:B→AS是任意S-同态.定义映射h:C→AS为:对任意的c∈C,任意的t∈S,令

其中a∈A是事先任意固定的一个元素,且对于t∈S,存在v∈S使得t=vt(因为S是有弱局部单位半群).由于ϕ是单同态,所以ϕ−1(tc)是唯一的.因此h是从C到AS的映射.下证h是S-同态.对任意s,t∈S,有

故h(sc)=sh(c),即h是S-同态.又因为对任意的b∈B,任意的t∈S,有

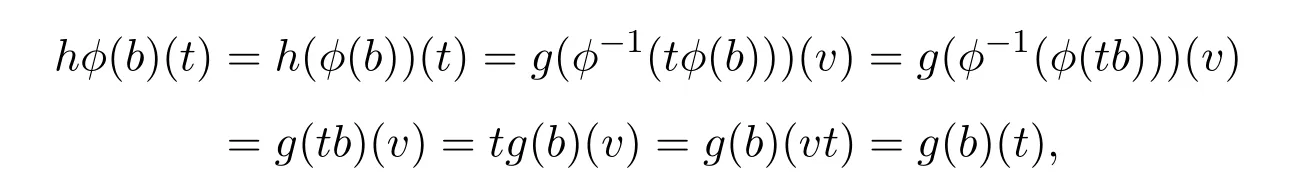
其中v∈S且t=vt,所以hϕ=g.因此AS是内射系.证毕.

推论 2.1设S有共同弱左局部单位半群,则任意酉S-系A可嵌入到一个内射系中.

证明由命题2.2知AS是内射S-系.作映射ϕ:A→AS:

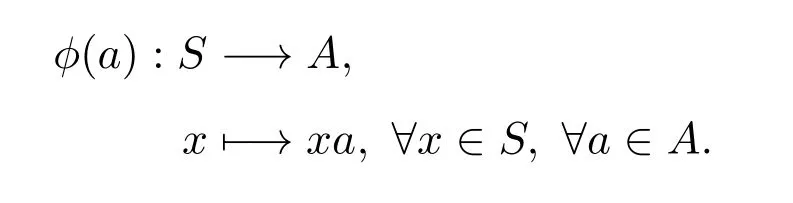
因为对任意的s,x∈S,任意的a∈A,有

所以ϕ(sa)=sϕ(a),即ϕ是S-同态.设a,b∈A使得ϕ(a)=ϕ(b).则对任意的x∈S,ϕ(a)(x)=ϕ(b)(x),即在A中有xa=xb.由于A是酉左S-系,所以对于a和b存在u,v∈S以及a′,b′∈A,使得a=ua′,b=ub′.又因为S有共同弱左局部单位,所以对于u,v∈S,存在w∈S,使得wu=u,wv=v.因此,

这说明ϕ是单同态.证毕.

现在可以给出内射系的等价刻画.

定理 2.1设S是半群,则E是内射S-系,当且仅当函子 HomS(−,E)(从左S-系范畴到集合范畴)把单同态变为满映射.

证明对任意的S-单同态f:A→B,若g:A→E是S-同态,则由E的内射性知,存在S-同态h:B→E使得g=hf,即

这说明Hom(−,E)是把单同态变为满映射.

反过来,假设f:A→B是任意的S-单同态.由于函子Hom(−,E)将单同态映成满映射,所以映射Hom(f,E):Hom(B,E)→Hom(A,E)是满的,即对任意的S-同态g:A→E,存在S-同态h:B→E使得下图可换:

这说明E是内射S-系.证毕.

特别地,当半群S有共同弱左局部单位时,则有下面结论.

定理 2.2设S是有共同弱左局部单位半群,则以下几条等价:

(1)E是内射S-系;

(2)任意的S-单同态f:E→A是可收缩的;

(3)存在S-系B以及可收缩的S-单同态f:E→BS.

证明(1)⇒(2)对任意的S-单同态f:E→A,由E的内射性可知,存在S-同态g:A→E使得gf=1E,故f是可收缩的.

(2)⇒(3)令B=E,由推论 2.1的证明可知,存在S-单同态f:E→ES.由条件(2)知f是可收缩的.

(3)⇒(1)由命题2.2可知,BS是内射系.再根据命题2.1,E是内射系.证毕.

注 2.1在定理2.2中,当有共同弱左局部单位半群S是幺半群时,即得幺半群的内射系的刻画(参见文献[7]).

下面讨论内射S-系的若干性质.

命题 2.3设S是半群,则任意的内射S-系必含有零元.

证明设E是内射S-系.记S0=S˙∪{θ},其中{θ}是单元S-系.显然有S-单同态f:S→S0.取定x∈E,对任意的s∈S,定义S-同态gx:S→E为gx(s)=sx.由E的内射性知,存在S-同态h:S0→E,使得hf=gx.记h(θ)=a∈E.则对任意的s∈S,

即a是E的零元.证毕.

3 内射系对半群的刻画

本节讨论S-系A的内射性与A上方程组的可解性之间的密切联系,进而给出所有S-系是内射的半群的刻画.

设A是S-系.A上的任意方程应具有下列三种形式之一:

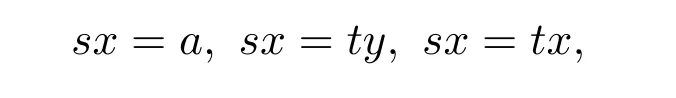
这里s,t∈S,a∈A,x,y是未定元.A上任意方程组都是若干个(有限或无限)上述方程构成的集合.记A上的方程组中所含方程的个数为|Σ|.

设S是半群,A,B是左S-系.记A≤B为A是B的子系,或B是A的扩张.

定义 3.1称S-系A上的方程组Σ是容许的,如果Σ在A的某个扩张系中有解.

下面给出S-系A的内射性与A上方程组的可解性之间的联系.

定理 3.1对于任意的有弱左局部单位半群S和任意的S-系A,以下两条等价:

(1)A是内射的;

(2)A上的任意容许方程组在A中有解.

证明(1)⇒(2)设Σ是A上的容许方程组,则必存在A的扩张系B,使得Σ在B中有解.因为A是内射的,所以自然包含同态A→B是可收缩的,即存在S-同态f:B→A使得f|A=1A.显然f把Σ在B中的解变为Σ在A中的解.

(2)⇒(1)设B是A的扩张系,则存在B−A的子集合C使得B=A∪(∪c∈CSc).定义A上的方程组:

显然Σ在B中有解{c|c∈C},所以Σ是A上的容许方程组.因此由条件(2)知Σ在A中有解,设解为{ac|c∈C}.定义映射ϕ:B→A为

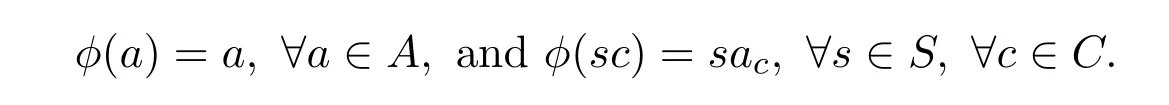
容易验证ϕ是有定义的,且ϕ是S-同态,ϕ|A=1A.所以包含同态A→B是可收缩的,故A是内射系.证毕.

定理3.1表明,有弱左局部单位半群的S-系的内射性可通过A上容许方程组的可解性来刻画.在幺半群理论中,可利用S-系的绝对纯性来刻画所有S-系是内射的半群.下面将这一理论方法应用到有局部单位半群理论中.为此先给出内射系的一个重要特征.

命题 3.1设S是有弱左局部单位半群,则S-系A是内射的,当且仅当A没有真的基本扩张.

证明设A是内射的,B是A的基本扩张.则包含同态A→B是可收缩的,所以存在S-同态g:B→A,使得g|A=1A.由于B是A的基本扩张,所以g是单的.因此,A=B.

反过来,设A没有真的基本扩张.假设B是A的真扩张.则A不是B的基本子系,所以存在B上的同余1B,但λ限制在A上时为恒等同余.令

由Zorn引理知D中有极大元,设其为λ,从而知A≃A/λ,且B/λ是A/λ的基本扩张,所以A/λ=B/λ.因此,对任意的b∈B,存在唯一的a∈A使得 [a]λ=[b]λ.规定S-同态f:B→A为f(b)=a,b∈B.则f|A=1A,所以S-同态A→B可收缩.这就证明了A是内射系.证毕.

下面的定理给出任意S-系都有内射的基本扩张.

定理 3.2设S有共同弱左局部单位半群,A是S-系,则存在内射的S-系B使得B是A的基本扩张.

证明由推论2.1可知存在内射的S-系E使得A≤E.令

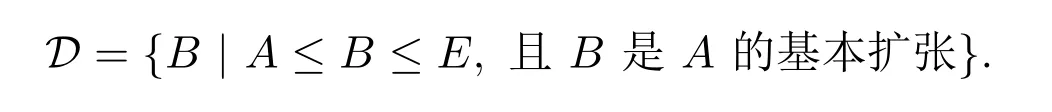
则.设{Bi|i∈I}是D中的升链.令.容易验证B是A的基本扩张.所以由Zorn引理知D中有极大元,设其为B.若C是B的基本扩张,则C就是A的基本扩张,所以B=C.这说明B没有真的基本扩张,因此由命题3.1知B是内射的.证毕.

注 3.1由命题3.1知,S-系的内射的基本扩张在同构意义下是唯一的.

定义 3.2设S是半群,A是B的子系,α是无穷基数.称A在B中是α-纯的(或称A是B的α-纯子系),如果A上只有一个未知元且满足|Σ|<α的任意方程组Σ,若Σ在B中有解,则在A中一定有解.如果A在它的任意扩张系中都是α-纯的,那么就称A是α-绝对纯的.如果任意S-系都是α-绝对纯的,那么就称半群S是完全α-绝对纯的.

最后给出所有S-系是内射的有共同弱左局部单位半群特征.下面定理的证明类似于文献[14]中命题1.2的证明,为了论文的完善,这里将给出完整的证明.

定理 3.3设S有共同弱左局部单位半群,α是无穷基数且α>|S|,则如下两条等价:

(1)S是完全α-绝对纯的;

(2)任意S-系都是内射的.

证明(2)⇒(1)由定理3.1即得结论.

(1)⇒(2)设A是S-系.下证A是内射系.由定理3.2知存在内射的S-系I(A)使得I(A)是A的基本扩张.令

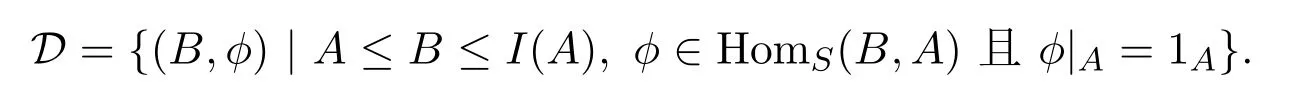
因为 (A,1A)∈D,所以D∅.设 (B1,ϕ1),(B2,ϕ2)∈D,规定

D关于≤构成一个半序集.容易验证D中的任意升链都有上界.故由 Zorn引理知D中有极大元,设其为 (B0,ϕ0).下证B0=I(A).否则若B0(A),则存在b∈I(A)−B0.令C=B0∪Sb.则A≤C≤I(A).考虑方程组:

Σ只有一个未知元x,且|Σ|≤|S|+|S|2<α.又 Σ在I(A)中有解b,故由B0的α-绝对纯性知Σ在B0中有解,设其为a0∈B0.作同态ϕ:C→A为:

设sb=tb.则方程sx=tx∈Σ.所以有sa0=ta0,故

若存在s∈S,使得sb=a∈B0,则方程sx=a∈Σ.故有sa0=a.所以

这说明了ϕ是映射.显然ϕ还是S-同态.因为ϕ|A=ϕ0|A=1A,所以(C,ϕ)∈D.又显然 (B0,ϕ0)≤(C,ϕ)但 (B0,ϕ0)̸=(C,ϕ). 这与 (B0,ϕ0)的极大性矛盾.所以B0=I(A).故存在S-同态ϕ0:I(A)→A,使得ϕ0|A=1A.这说明A是I(A)的可收缩子系.因此A是内射的.证毕.

注 3.2在定理3.3中,当有共同弱左局部单位半群S是幺半群时,即得幺半群的任意S-系都是内射的刻画(参见文献[14]).