时间离散的时滞三维K-型竞争扩散系统的行波解
2023-01-03 07:48:08彭华勤朱庆
纯粹数学与应用数学 2022年4期
彭华勤,朱庆
(广西师范大学数学与统计学院,广西 桂林 541004)
1 引言
根据物种的多样性,种群之间的相互作用普遍存在,因此研究物种间的相互作用一直是生物数学中的一个重要课题.行波现象广泛存在于各学科中,它能够解释自然界中的许多现象而备受学者们关注[1-3].时滞现象在日常生活中经常发生,在研究人口动力学,种群生态学,传染病学等学科时通常需要考虑时滞所带来的影响,对具有时滞反应扩散方程的行波解已经被广泛地研究[4-7].对连续模型进行离散化是得到离散模型的一种方法,离散化后的模型通常具有非常丰富的动力学性质,并且在描述时空现象中也起到了十分重要的作用,因此对这类系统已有深入的研究,相关的理论研究包括行波解和渐近传播速度[8-16].

2 一般理论
在本文中,将使用R3中的标准序,首先给出系统(3)的行波解的概念.




3 系统 (4)行波解的存在性



4 应用







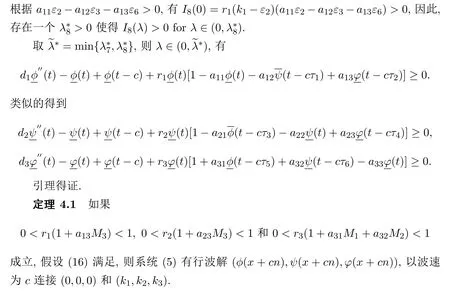
猜你喜欢
数学物理学报(2022年5期)2022-10-09 08:57:42
今日农业(2022年15期)2022-09-20 06:54:16
数学物理学报(2020年5期)2020-11-26 06:06:48
红土地(2018年7期)2018-09-26 03:07:38
成都信息工程大学学报(2018年1期)2018-05-31 08:40:38
天津师范大学学报(自然科学版)(2015年2期)2015-03-11 18:46:50
四川师范大学学报(自然科学版)(2015年2期)2015-02-28 14:07:40
广西科技大学学报(2015年4期)2015-02-27 12:22:22
应用数学与计算数学学报(2014年3期)2014-09-26 12:03:52
当代畜禽养殖业(2014年10期)2014-02-27 07:59:49

