基于CFD的水动力与泥沙输移模型研究及其在海洋海岸工程中的应用

梁丙臣，杨博，张嶔

（1.中国海洋大学工程学院,山东青岛 266100；2.山东省海洋工程重点实验室,山东青岛 266100）

海洋作为地球上最为广阔的水体，除了蕴藏着大量的清洁能源（波浪能、潮流能）之外，其底部同样贮藏着十分可观的油气和矿产资源。巨量的资源储备刺激着人类对海洋探索的脚步，同时，科技的迅速发展为人类探索海洋提供了重要的技术保障。随着人类海洋工程活动越发频繁，大量的桩基、管线、生产井及注入井等基础设施布置于海床中，同时海底集矿机等工程设备也会在海床附近开展工作。因此无论是在工程前期施工还是设施后期工作（运营）的过程中，都不可避免地存在流体-结构物-泥沙相互作用。这种相互作用在波流、地形、床面泥沙组分及结构物几何特征等参数的影响下变得十分复杂，并且在极端情况下会对基础设施或工程设备的结构安全产生严重破坏，甚至对海洋生态环境产生恶劣的影响。

在海洋工程建设和发展的历程中，发生过多起由流体-结构物-泥沙之间复杂的相互作用引发的结构破坏事故[1-3]。海洋工程设施或者结构物附近的泥沙冲刷都是导致其发生结构破坏的重要原因。对于桩基础而言，基础冲刷会大幅度减小桩基的入土深度。例如，和庆冬和戚建功[4]监测了某海上风电场运行1 a后25个风机基础桩周围的冲刷过程，发现所有桩附近均存在不同程度的冲刷坑，其中最大冲刷深度约为7.33 m，冲坑范围约为50 m。桩基础附近过度的冲刷会造成基础的承载能力降低、桩基的倾覆力矩增加以及其结构自振频率降低等问题[5]，从而对风电场的后续稳定运行造成较大的安全隐患。对于管线而言，局部冲刷会导致管线在冲刷坑的上方形成悬空段。例如，黄明泉等[6]通过无人有缆遥控水下机器人对东方1-1海管进行了6 a的连续观测，在较强的海流影响下，海管下方形成了多段悬跨区域，悬跨段总长度由2014年的4 446 m增长至2019年的6 498 m，且单段最大悬跨长度已达49.47 m，最大悬跨高度已达2.21 m。悬跨段的管线在海流和地形的影响下其局部流场特征会发生较大变化，从而改变管线的受力特性导致其发生变形或者振动，增加发生结构破坏的风险。

另外，在工程施工阶段或者深海采矿过程中，工程设备（如集矿机等）在海底工作过程中势必会对床面产生扰动从而在海底产生扰动泥沙羽流。泥沙羽流中多包含较细粒径的黏性泥沙颗粒，在强烈的床面扰动以及海流等因素的影响下，这些泥沙颗粒将会扩散到很远的地方才会重新沉积到床面[7]。海床被扰动后，原本贮藏于海床之下的某些有毒物质（如重金属等）会随着泥沙羽流的运动一同扩散到水体中[7]。因此，泥沙羽流的悬扬和扩散以及在其他区域的重新落淤都会对该海域的海洋环境产生十分严重的影响，甚至会造成该海域生物多样性的丧失[8]。

综上所述，无论是从基础设施结构安全角度还是从保护海洋环境的角度，深入探究流固耦合过程中的流场、水动力特征及泥沙输移机理都具有十分重要的工程意义。然而，由于海洋环境、观测设备及试验场地等多重因素的限制，无法仅通过现场观测或者物理模型试验的方法对复杂条件影响下的局部流场结构和泥沙输移开展详细的研究。超级计算机技术的发展以及开源计算的逐渐普及促进了数值模拟技术的发展，极大地提高了流场精细化模拟的效率。并且，相比于现场观测或者物理模型试验的方法，从数值模拟中可以获取更为细致的流场结构特征。因此，通过数值模拟方法对复杂流场水动力及泥沙输移过程开展分析已经成为当前的研究热点。

本文针对海洋、海岸工程中局部流场及泥沙输移问题的数值模型开展研究，探究了各类水动力模型和泥沙输移模型的优缺点，分析了各类模型在海洋、海岸工程中的适用范围及应用现状，为各类模型的发展及其工程应用提供参考依据。

1 水动力数值模型发展及应用

数值模拟即通过特定的方法求解流体运动的基本方程以得到流场内基本物理量的分布特征的方法，在海洋工程数值模拟中应用最为广泛的为计算流体力学（Computational Fluid Dynamics，CFD）方法。在CFD中需要通过特定的离散方法在计算网格上离散描述流体运动的Navier-Stokes方程组，并通过适当的求解算法求解离散后的代数方程组获得流场变量在空间离散点处的近似值[9]。另外，近年来基于拉格朗日方法的光滑粒子流体动力学（Smoothed Particle Hydrodynamics，SPH）方法同样被应用于海洋工程数值模拟中，其无网格的特性使其非常适合模拟存在复杂边界动力过程的问题，如波浪模拟[10-12]或存在较大边界位移的情况[13]，该方法还同样应用于存在颗粒流动[13-15]的数值模拟中，如图1所示。

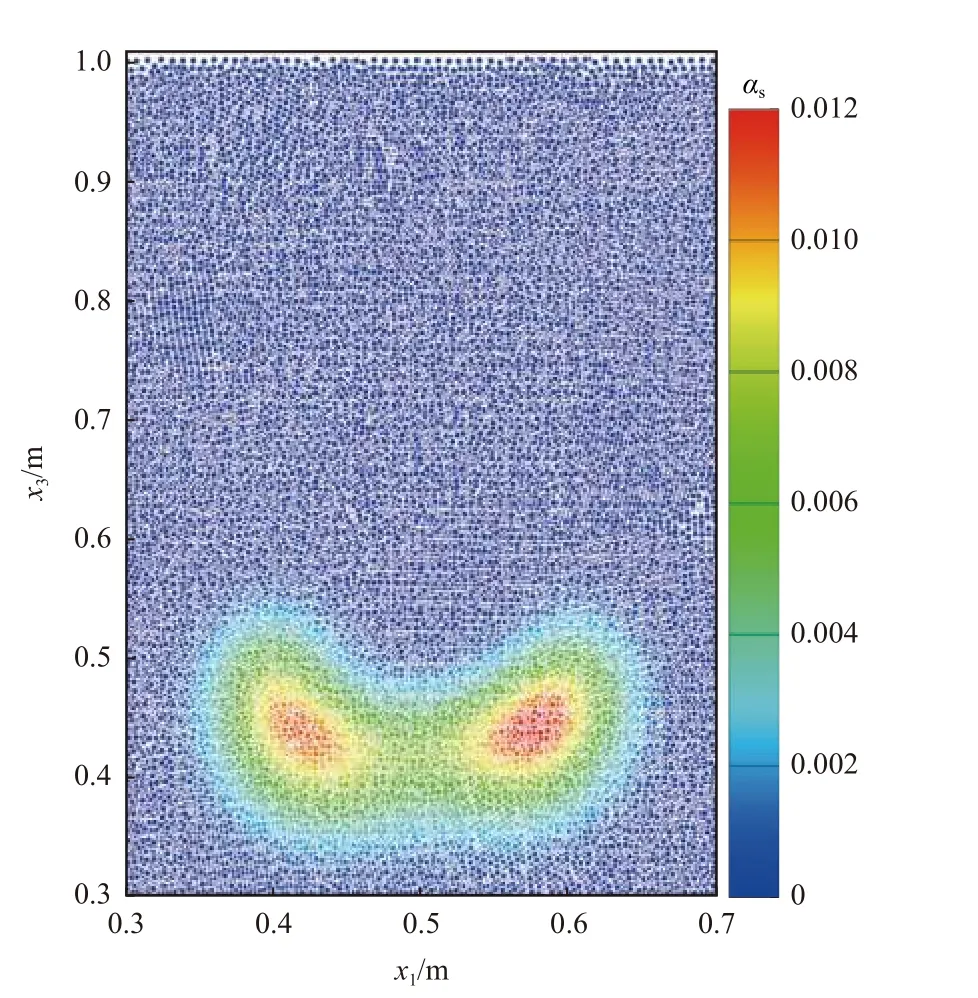
图1 基于SPH方法模拟的泥沙颗粒云沉降过程中的泥沙分布Fig.1 Sediment distribution during sediment cloud settling based on SPH method simulation

除了模拟方法之外，数值模拟中另外一个不可被忽略的因素即对湍流的模拟。在海洋工程问题中，由于受到各种复杂因素的影响，流体的流动多处于湍流状态，因此准确地模拟流动中的湍流特征对数值模拟的精度至关重要。湍流数值模拟方法可以大体分为直接数值模拟（Direct Numerial Simulation，DNS）、雷诺平均（Reynoldsaverage Navier-Stockes，RANS）模拟和大涡模拟（Large Eddy Simulation，LES）。

1.1 直接数值模拟

直接数值模拟方法就是对瞬态 Navier-Stokes方程组进行直接离散求解，不需要对湍流流动做出任何简化，因此其模拟精度最高[9]。在DNS模拟需要较高的网格分辨率以解析到最小尺度的耗散涡（Kolmogorov尺度），考虑到三维流动问题，DNS模拟所需要的网格总数与Re9/4成正比[16]。在实际海洋工程中多为高雷诺数的复杂流动，且湍流脉动的频率较高，在DNS模拟中需要极其微小的空间和时间步长[9]，导致计算成本极高。目前DNS方法主要应用在低雷诺数时几何布局较为简单的工况的数值模拟中[17-29]，如图2所示。

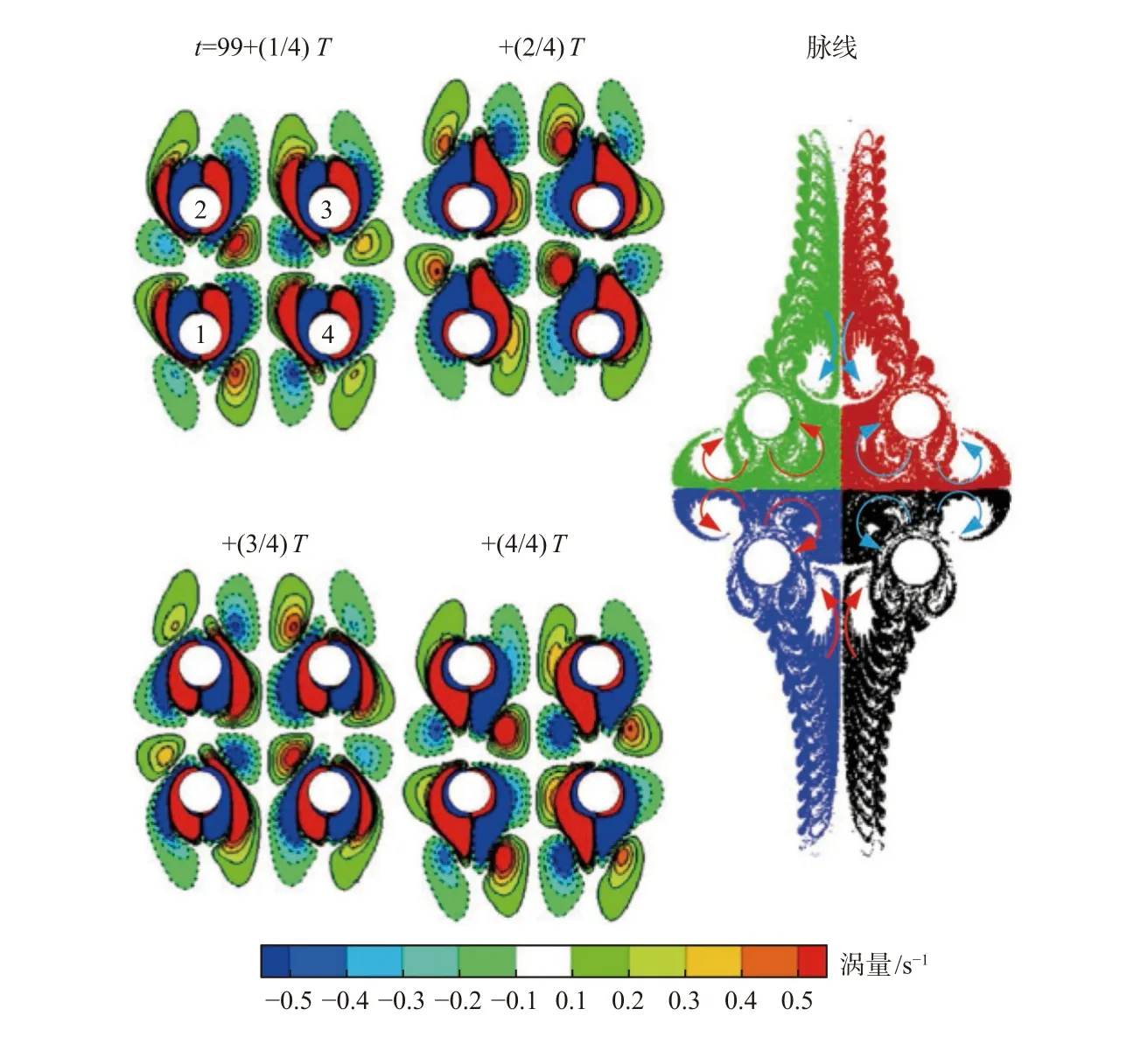
图2 震荡流作用下方形排列圆柱体局部涡量场及脉线Fig.2 Vortex field and streaklinein squarely arranged cylinders under oscillatory flow conditions

1.2 雷诺平均模拟

相比于DNS方法，RANS方法在复杂流动问题的数值模拟中应用较为广泛。这是因为，在工程中更注重由湍流运动所引起的时均流场的变化[9]。在RANS方法中求解的是时均化的Navier-Stokes方程组，通过引入湍流模型来计算由流速脉动产生的Reynolds应力的影响[9]。根据Reynolds应力计算方法的不同，湍流模型可以分为Reynolds应力模型[30-31]和基于Boussinesq假定的涡黏模型[9]。涡黏模型中又根据湍流模型方程数量可进一步分为零方程模型[32]、单方程模型[33]和双方程模型[34-37]，其中双方程湍流模型在海洋工程数值模拟中使用最为广泛。RANS方法模拟中计算量较小（lg Re 量级[38]），对复杂过程水动力过程的模拟效率较高，因此被大量学者应用于波、流水动力（波浪破碎或者波、流-结构物相互作用）过程[39-54]与涉及泥沙输移的结构局部冲刷[55-67]和岸滩演变[68-73]过程的研究。图3为基于RANS方法模拟的孤立波经过刚性植被群时候的波高及动能衰减过程。图4表明RANS方法可以准确地模拟复杂地形影响下的近岸波浪动力特征。

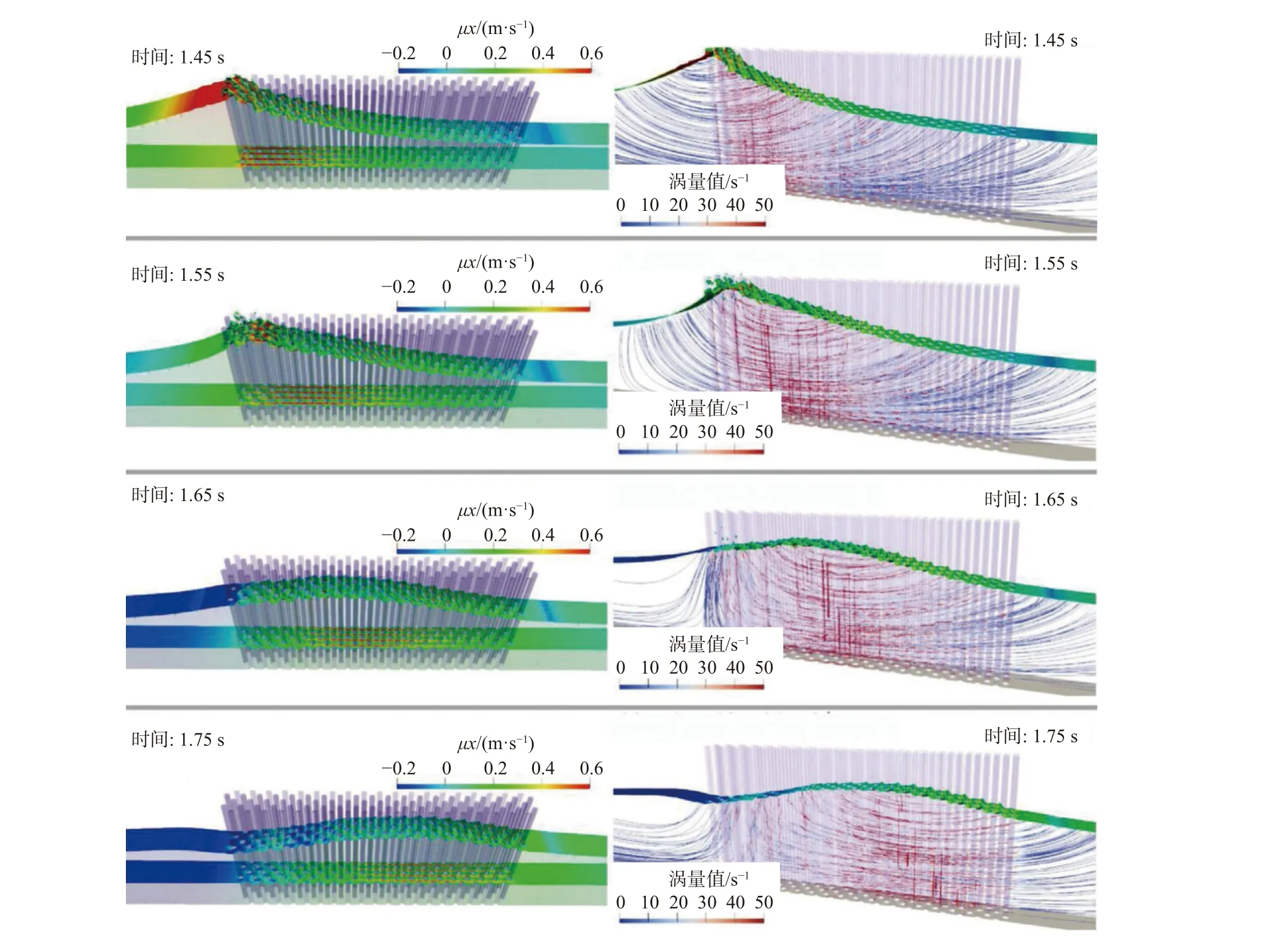
图3 基于RANS方法模拟的孤立波与刚性植被群相互作用过程中波面及流场变化特征Fig.3 Characteristics of wavesurface and flow field changesduring theinteraction between isolated wave and rigid vegetation clusters simulated based on the RANSmethod

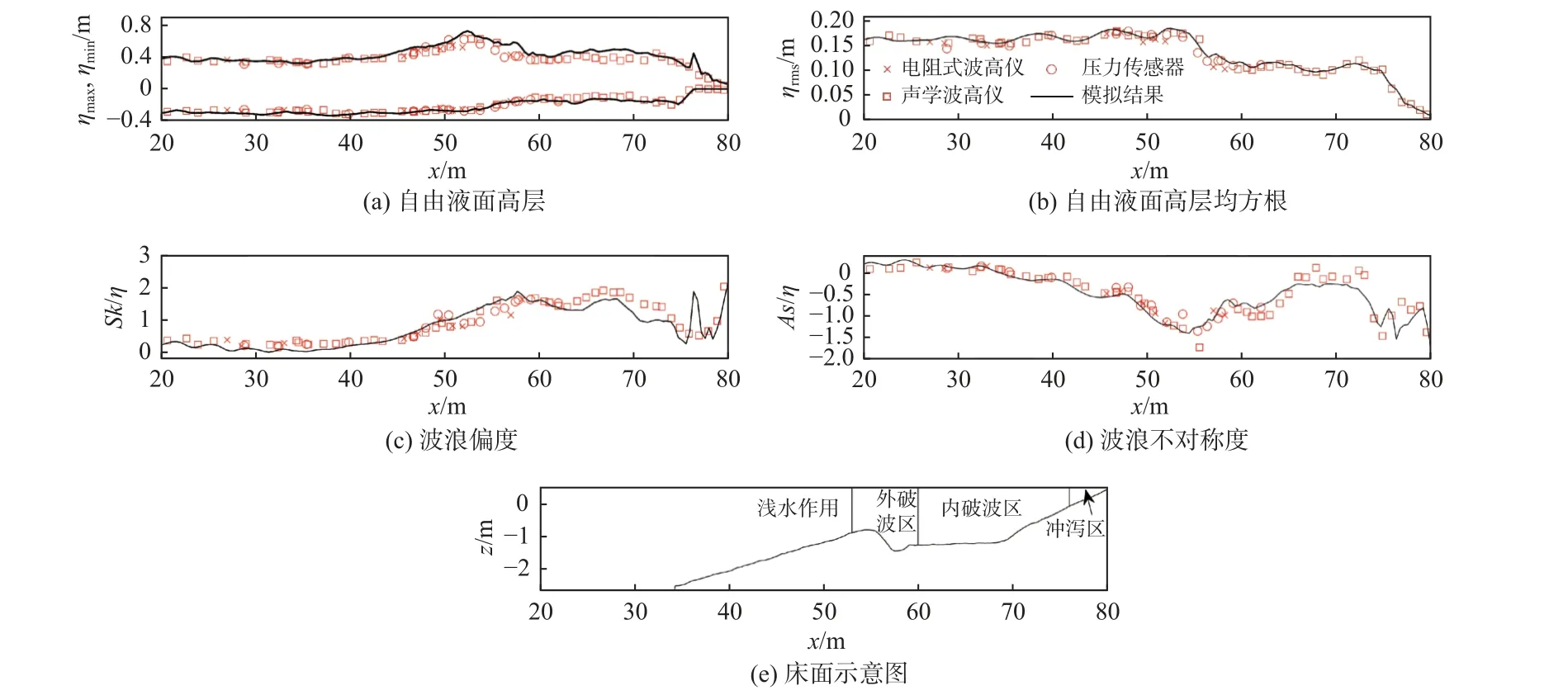
图4 沙坝上方卷破波动力过程的实验结果和RNAS模型模拟结果对比Fig.4 Comparison of experimental and RNASmodel simulation resultsof thewavedynamicsof thewavebreaking above a sand bar

虽然RANS方法可以以较小的计算成本模拟工程中的复杂流动过程，但是该方法无法准确模拟复杂流动中细部流场结构特征，例如，RANS方法无法在非定常流动（Unsteady-ReynoldsAverage Navier-Stockes，URANS）中准确模拟钝体结构表面流动分离过程[74-75]。

1.3 大涡模拟

LES方法是一种介于DNS方法和RANS方法之间的湍流数值模拟方法，其基本思想为通过瞬态Navier-Stokes方程组求解比网格尺度大的湍流运动，而小尺度涡对大尺度涡的影响则通过亚格子尺度模型（SubGrid-Scale model，SGS）在针对大尺度涡的瞬态Navier-Stokes方程组中体现出来[9]。其中广泛使用的SGS模型为Smagorinsky模型[76]、单方程模型[77]和WALE（Wall Adapting Local Eddy-viscosity）模型[78]等。

在海洋工程中，LES方法主要应用于波浪破碎[79-83]及波、流-结构物相互作用过程[51,83-92]等流场水动力模拟和复杂水动力过程影响下的悬沙（泥沙羽流）输移数值模拟中[82,93-99]。利用LES方法模拟可以更为精细地捕捉波浪破碎或者钝体绕流过程中的湍流涡结构变化特征[82,88]（图5和图6）。众多学者[52,98]通过对比RANS方法和LES方法的模拟结果证明了LES方法在模拟复杂流场湍流特征上具有更高的精度（图7）。但是，LES方法在局部冲刷过程的数值模拟中应用较少，Liang等[56]利用LES方法和RANS方法分别对二维的管线冲刷开展数值模拟,结果发现在二维情况下LES方法无法准确模拟管线下游的流速和压力场变化，进而导致LES方法模拟的冲刷地形精度低于RANS方法的模拟结果（图8）。

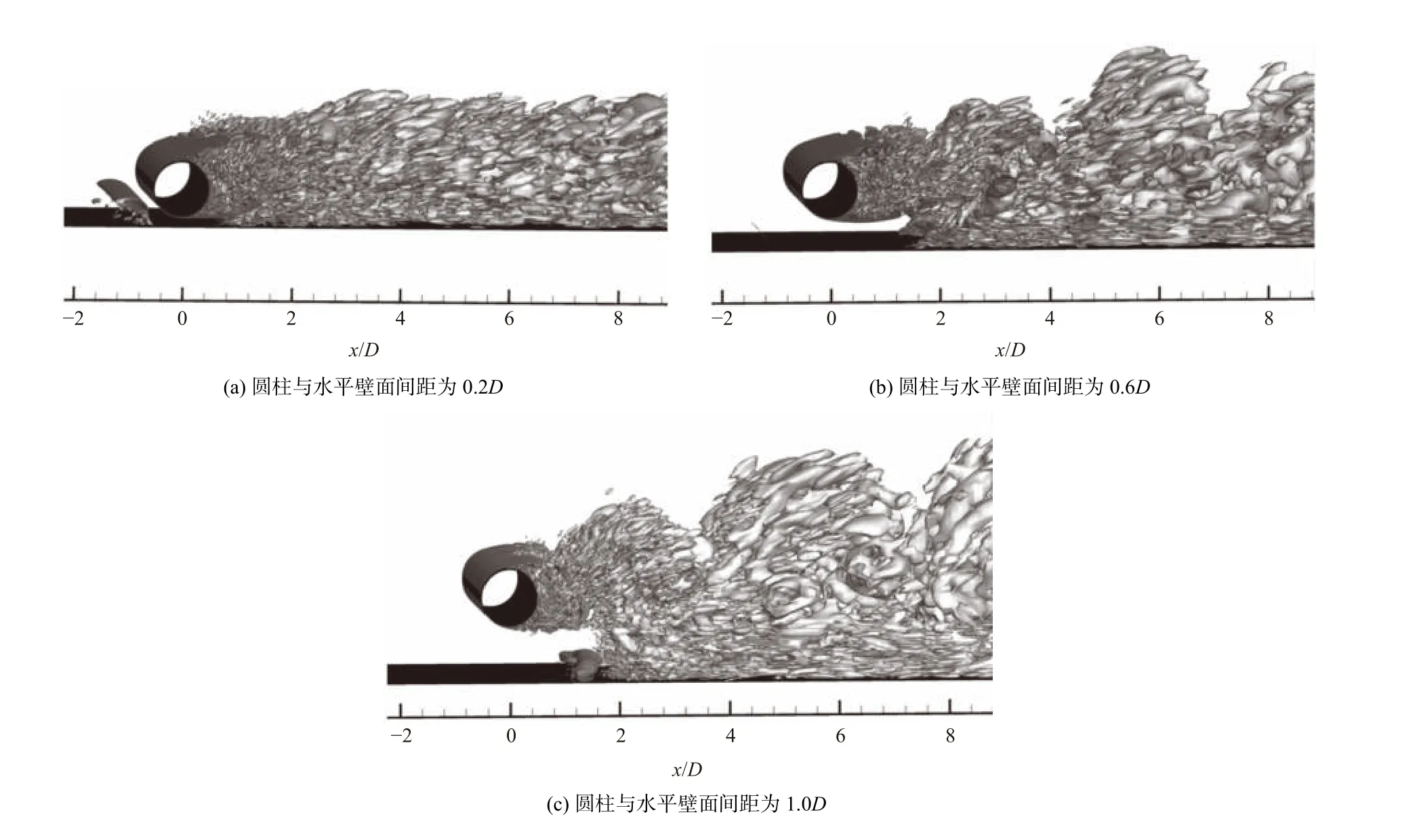
图5 LES方法模拟的Re=20 000时近水平壁面圆柱绕流尾迹涡结构特征Fig.5 The structural characteristics of the near-horizontal wall cylindrical wake vortex simulated by the LESmethod at Re = 20 000

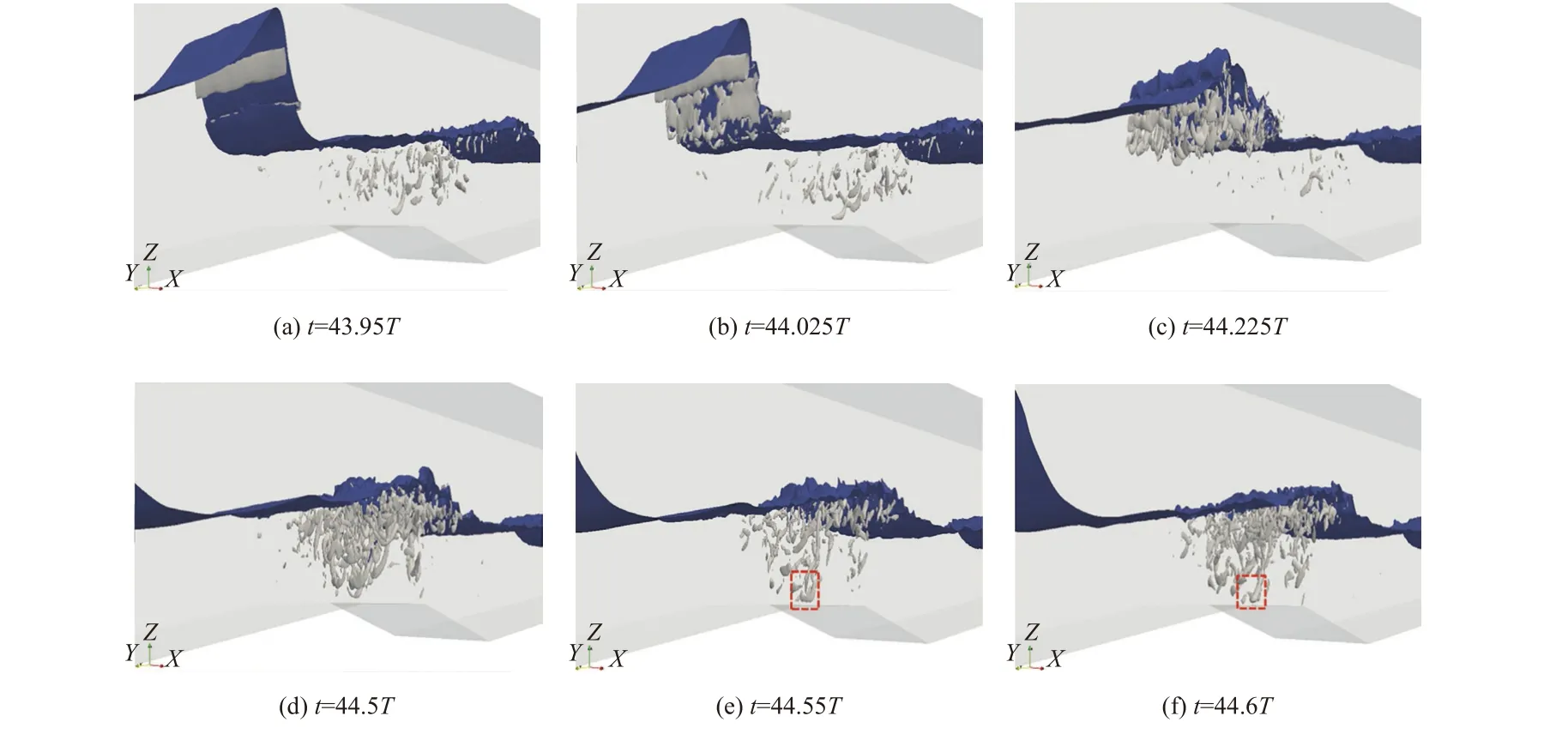
图6 基于LES方法模拟的破碎波波峰下方的湍流相干结构Fig.6 Turbulent coherent structure below the crest of a breaking wave based on LESmethod

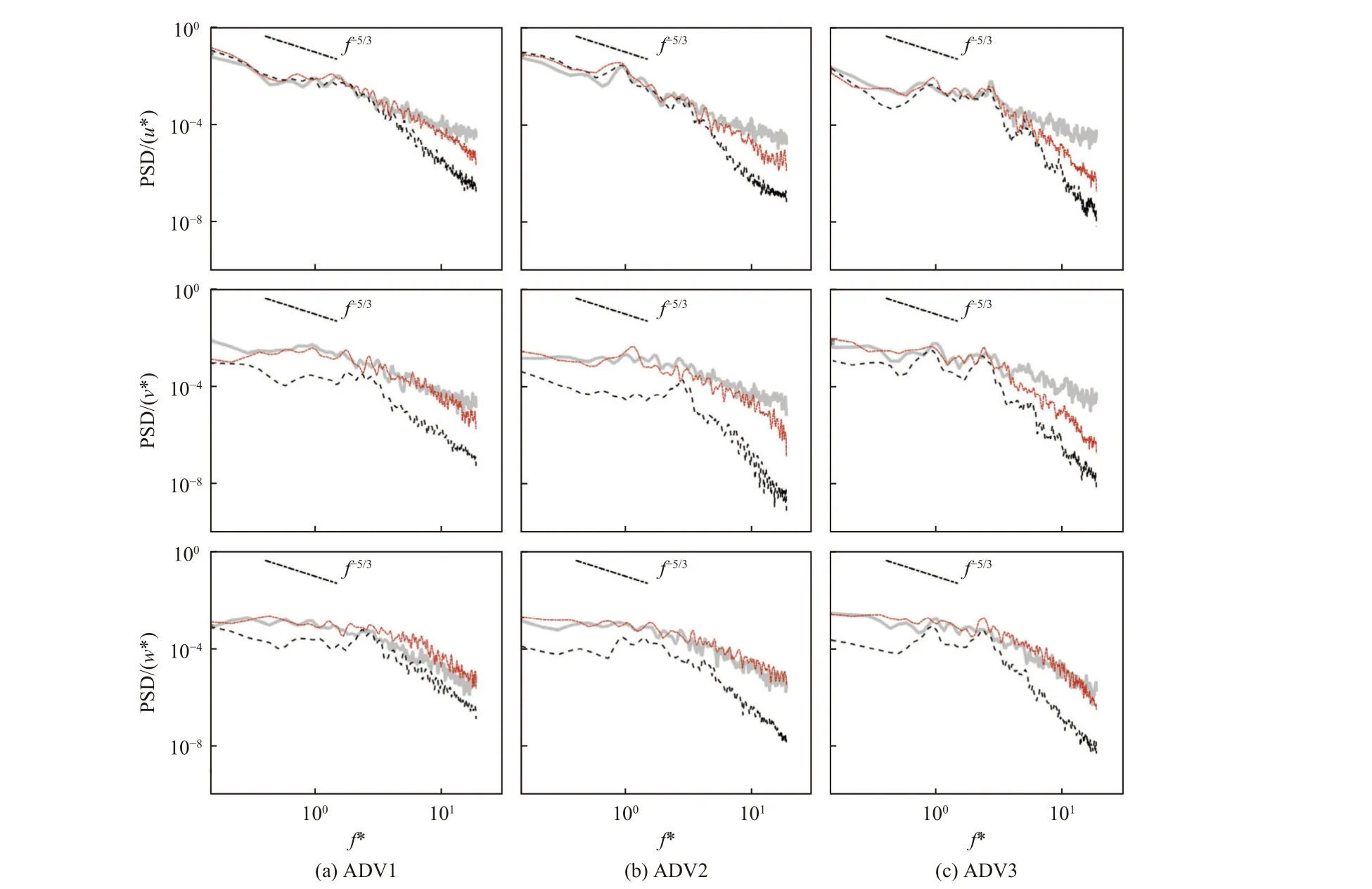
图7 随机波与护堤上方柱结构簇相互过程中不同位置处的流速波动功率谱对比图Fig.7 Comparison of the power spectra of flow velocity fluctuationsat different locations during the interaction between the random wave and the cluster of squarecolumn structures on the berm

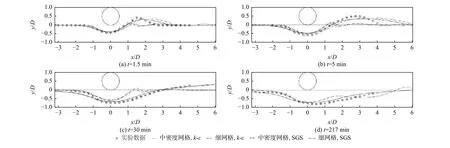
图8 LES方法及RANS方法模拟管线局部冲刷过程地形剖面对比图Fig.8 Comparison of the bed profiles of the LESand RANSsimulating the local scouring processof the pipeline

LES方法相比RANS方法具有更高的模拟精度，同时比DNS模拟具有更小的计算量。在结构物绕流问题的LES模拟中，自由流动区域的计算量仅为Re0.4量级，但是在近壁面边界层区域的计算量仍需要Re1.76量级[38,100]，因此利用LES方法对高雷诺数的近壁面流动开展数值模拟仍然较为困难。

1.4 RANS/LES混合

RANS/LES混合方法的基本思想是在近壁面区域应用计算量较小的RANS方法来模拟近壁面时均流动特征，而在自由流动（或者分离流动）区域利用LES方法来精确解析流场（尾迹）中的瞬时涡结构变化[101]。由于RANS/LES混合方法并不解析近壁面区域的湍流涡结构，其计算量与LES方法相比减小了约0.07Re0.46倍[102]。基于上述概念，不同学者开发了多个RANS/LES混合模型，Fröhlich和Von Terzi[101]按照不同的物理模型假定将RANS/LES混合模型分为界面类[103-105]、嵌入式类[106-107]以及第二代URANS类[108-110]等。李钊[111]和吴迪[112]则对不同种类的混合模型的具体特点以及研究现状给出了更为细致的讨论。

在众多RANS/LES混合模型中，目前发展较为成熟且在工程中应用较广的为在界面类中的分离涡模拟（Detached-eddy-simulation，DES）模型类[111-112]。DES模型类最早是由Spalart[103]在单方程Spalart-Allmaras 模型[32]的基础上构建的RANS/LES混合模型（SA-DES）。DES模型根据网格点到壁面的距离以及网格长度尺度之间的大小关系定义了湍流特征长度，并基于此特征长度实现了在不同区域内由RANS模型向LES模型的转换。在近壁面区域Spalart-Allmaras模型为标准的RANS模型，而在自由流动或者分离流动区域Spalart-Allmaras模型转换为单方程的SGS模型。SA-DES的基本思想也可以是与其他RANS模型相结合构建相应的混合模型，如基于k − ωSST的DES模型（SST-DES）[113]。

Menter等[37]在利用DES方法模拟机翼表面的边界层分离流动时发现，当机翼附近的最大网格长度hmax细化到hmax/δ<0.5～1.0时（δ为边界层厚度）会发生错误的边界层分离现象（图9）。这种分离现象是由于网格造成的，因此该现象也被称为网格诱导分离（Grid Induced Separation，GIS）[37]。Spalart等[104]认为出现GIS是由于在边界层内发生了由RANS向LES的提前转换，但是边界层内的网格分辨率不足以保证LES模型产生足够的雷诺应力，使边界层内的涡流黏度降低进而发生分离所致。Spalart等[104]将这种现象命名为模拟应力耗尽（Modeled Stress Depletion，MSD）。

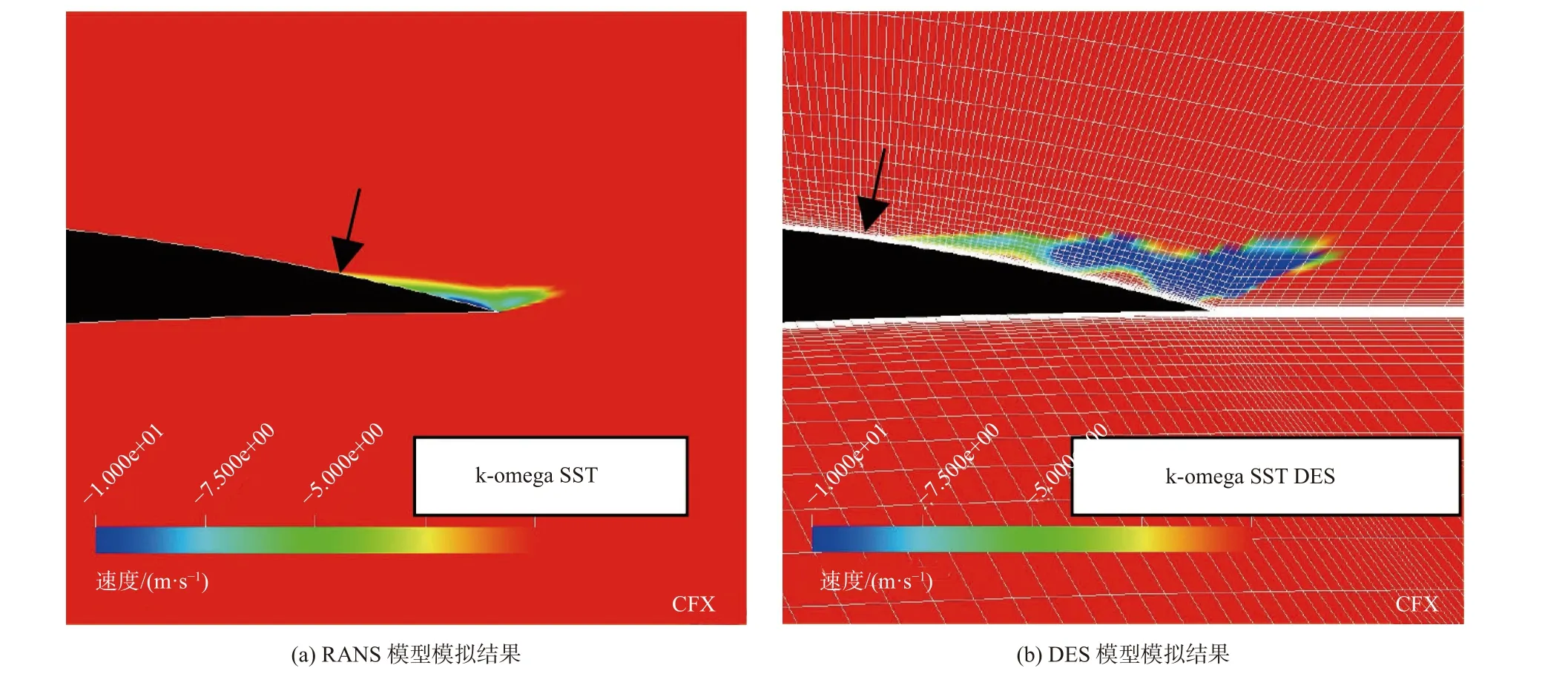
图9 机翼绕流中网格诱导边界层分离现象Fig.9 Themesh induces boundary layer separation in the wing circumference

为了解决DES模型中由于MSD造成的网格诱导分离现象，Spalart等[104]在SA-DES模型的基础上发展了延迟分离涡模拟模型（Delayed-Detached-Eddy Simulation，DDES）。在DDES模型中的湍流特征长度中引入一个延迟函数，在边界层内RANS计算区域延迟函数的值为1，而在边界层外的LES计算区域延迟函数的值会迅速变为0[104]。该方法可以有效地阻止在某些特定的网格密度条件下边界层内的RANS计算模式向LES计算模式的转换。同样，Gritskevich等[105]基于SST-DES模型提出了SST-DDES模型。

除了GIS现象之外，在原始的DES模型中还存在对数层不匹配（Logarithmic-Layer Mismatch，LLM）以及灰区等问题[114]，DDES模型中同样继承了这一问题。为此Shur等[115]将DDES方法与壁面建模LES模型（Wall-Modelled LES，WMLES）相结合，提出了改进的延迟分离涡模拟模型（Improved Delayed-Detached- Eddy Simulation，IDDES）。IDDES模型很大程度上缓解了DES和DDES方法中模拟的对数层和解析的对数层不匹配的问题，同时使区域型的WMLES模型更加便捷地应用于复杂流场的模拟中[115-116]。当入流中包含足够的湍流信息时，IDDES方法能够促进边界层内的RANS模式向LES模式转换，此时IDDES模型中的湍流长度尺度更趋近于WMLES，而当入流中的湍流信息不足时，IDDES模型更趋近于DDES模型[112]。

在海洋工程中，DES类的RANS/LES混合模型除了被广泛地应用于高雷诺数条件下桩柱绕流[112,116-122]等大分离流动的模拟中外，近年来还陆续应用于旋翼流场、涡激振动/运动等复杂的流固耦合过程数值模拟中。Zhang和Jaiman[123]利用SA-DDES模型模拟了不同进速系数的导管桨尾流场特征，探索了涡流结构的演化以及尾流不稳定性（图10）。何聪等[124]利用SST-DDES方法模拟了不同流速和转速条件下的潮流能水轮机尾流场特征（图11），证明DDES方法可以有效模拟水轮机旋转过程中产生的叶尖涡、叶尖脱落涡、轮毂涡等涡结构，并且观察到完整的水轮机叶尖涡的产生、脱落、失稳、破碎过程。在涡激振动/运动方面，Joshi和Jaiman[125]提出了一种基于SA-DDES模型的有界的保正变分方法，并将其成功地应用到柔性立管涡激振动的模拟中。Xie等[126]和Zhao等[127]基于SST-DDES方法和overset动网格技术分别模拟了恒定流作用下的浮筒和半潜式平台结构的涡激运动特征。目前尚未发现DES类的RANS/LES混合模型应用到泥沙输移过程的数值模拟研究中的相关报道。

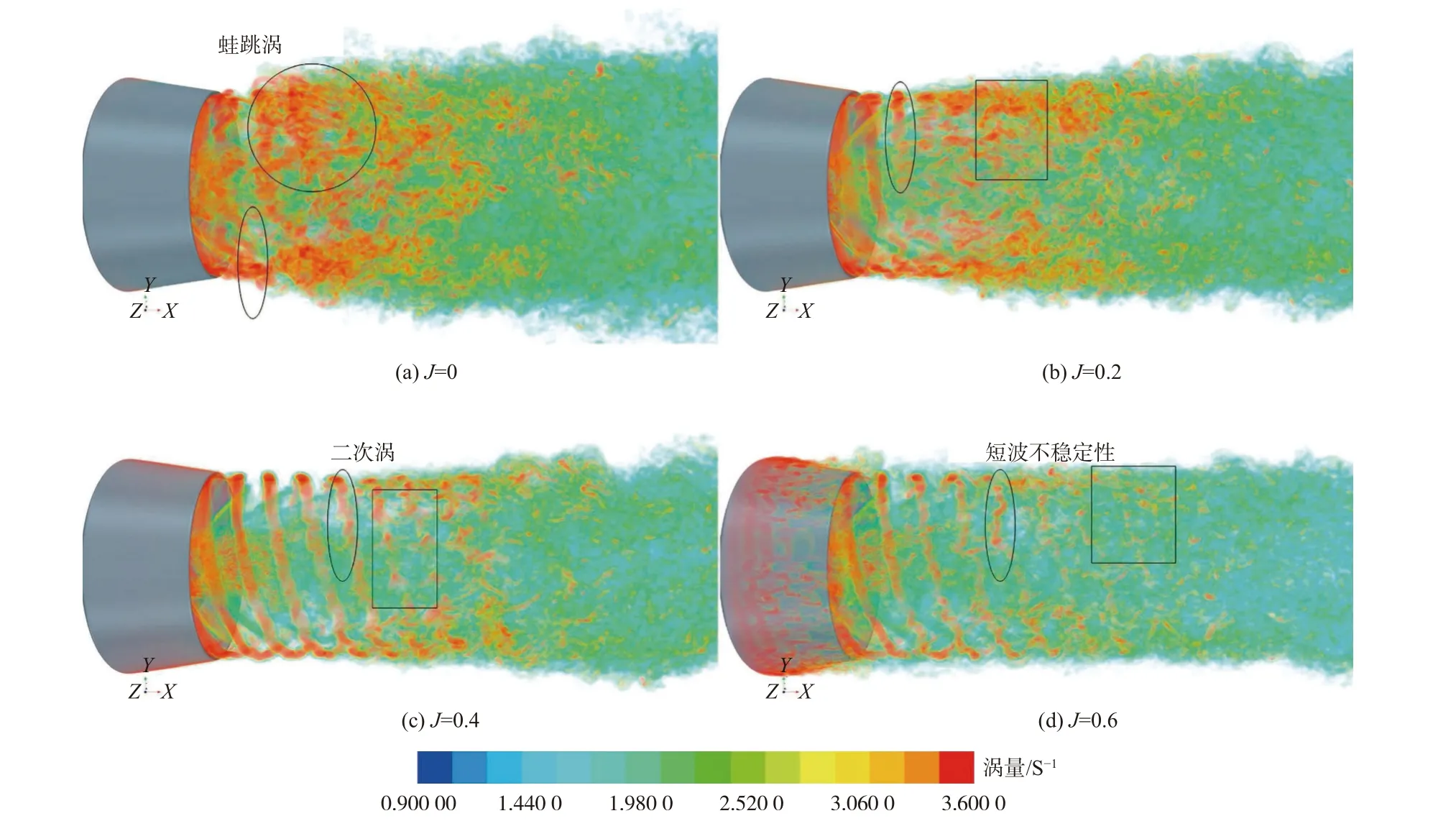
图10 基于DDES方法模拟的不同进速系数下的导管桨尾流涡量体积渲染图Fig.10 Volume rendering of the vortex in theducted propeller wake for different advance velocity factors based on DDESmethod simulations

图11 不同流速和转速条件下潮流能水轮机涡量场云图Fig.11 Vortex field clouds for tidal turbineunder different flow rates and speeds

2 泥沙输移数值模型发展及应用

在流体-结构物-泥沙相互作用过程的数值模拟中，对泥沙输移过程的模拟同样是当前研究的热点。由于泥沙的特殊性质以及水沙之间复杂的相互作用过程，导致对泥沙输移的模拟通常比流场水动力过程的模拟更为困难。目前，在工程中广泛使用的涉及泥沙输移问题的数值模型可以大体分为单相流模型以及两相流模型，在两相流模型中，根据对泥沙相不同的处理方法可进一步划分为欧拉-拉格朗日模型、两相流欧拉模型（欧拉-欧拉模型、双欧拉模型）以及两相流混合模型等。

2.1 单相流模型

单相流模型通过单相不可压缩流体Navier-Stokes方程组模拟水流的运动，而悬沙的输移则通过考虑泥沙沉降以及湍动扩散作用的对流扩散方程来求解。另外，泥沙床面上的推移质输移可通过经验性的推移质输沙率公式求解，如Meyer-Peter公式[128]、Engelund公式[129]以及VanRijn公式[130]等。

单相流模型通常与任意拉格朗日-欧拉（Arbitrary Lagrangian-Eulerian，ALE）动网格算法相结合实现对冲刷过程的模拟。ALE算法可以精确捕捉冲刷过程中的地形变化，因此该方法被众多学者植入到不同的CFD求解器/代码中开展对局部冲刷或者岸滩演变过程的模拟分析。例如，Brørs[55]、Zhao和Cheng[58]和Liu等[63]等基于有限元方法开发了局部冲刷模型并将其应用于波流作用下海底管线局部冲刷过程的模拟分析中，图12展示了管线冲刷模拟过程中的计算网格变化。Liu和Garcia[57]在OpenFOAM中植入了单相流ALE冲刷模型，随后Jacobsen[68]基于OpenFOAM中的有限面积算法进一步发展了冲刷模型，并将其应用到岸滩演变的模拟中（图13）。

图12 管线冲刷过程中网格变形Fig.12 Grid deformation during pipeline scouring

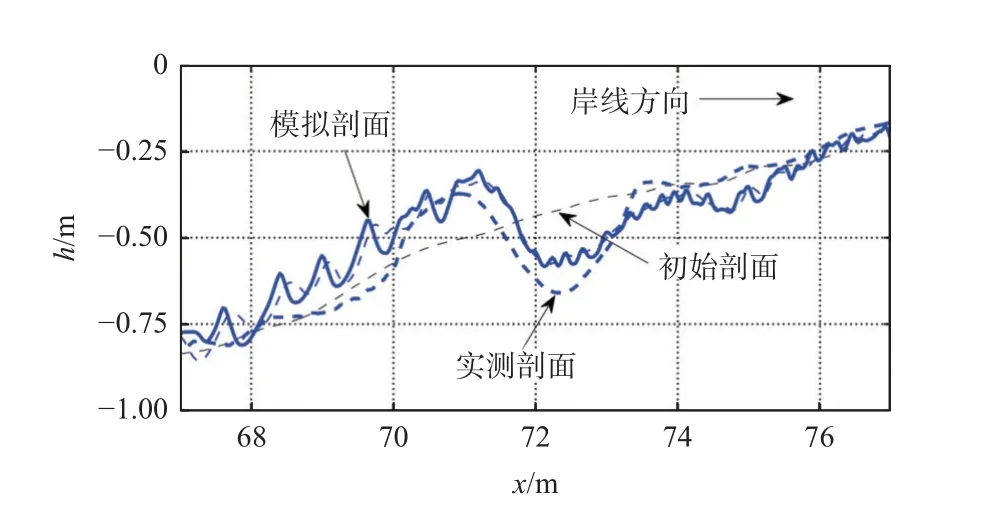
图13 规则波作用下沙坝剖面模拟值与实测值对比Fig.13 Comparison of simulated and measured values of sand bar profilesunder regular wave conditions

单相流模型除了与ALE动网格算法结合外，还可与level-set方法或者浸入边界法（Immersed Boundary Method，IBM）结合实现对冲刷过程中地形变化的模拟。Gautam等[67]在开源CFD代码REFF3D中植入了模拟波流耦合作用下局部冲刷过程的数值模型，该模型利用level-set方法同时来捕捉自由液面的变化以及冲刷床面的变化（图14）。Song等[131]在OpenFOAM中植入了一套基于浸入边界法（Immersed Boundary Method，IBM）的局部冲刷求解器“ibScour Foam”，并开源了相应的求解器代码（图15）。他们在求解器中植入了一种特殊的壁面函数[132]来克服IBM方法中壁面剪应力的非光滑性问题。相比于ALE动网格算法，IBM方法避免了在复杂地形时生成计算网格的困难及动网格计算中产生畸形网格而导致计算发散等问题[131]，但是在冲刷模拟中IBM方法的计算量较大。另外，从图16中可以看出IBM方法在对桩前最大冲刷深度的模拟精度略低于ALE动网格算法[133]的模拟精度。

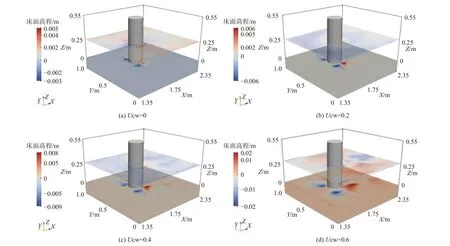
图14 基于level-set方法捕捉的波流耦合作用下桩柱冲刷过程中局部自由液面和床面地形变化特征Fig.14 Characteristics of freesurface and bed level changes during pilescouring under wave-flow coupling conditionscaptured by the level-set method

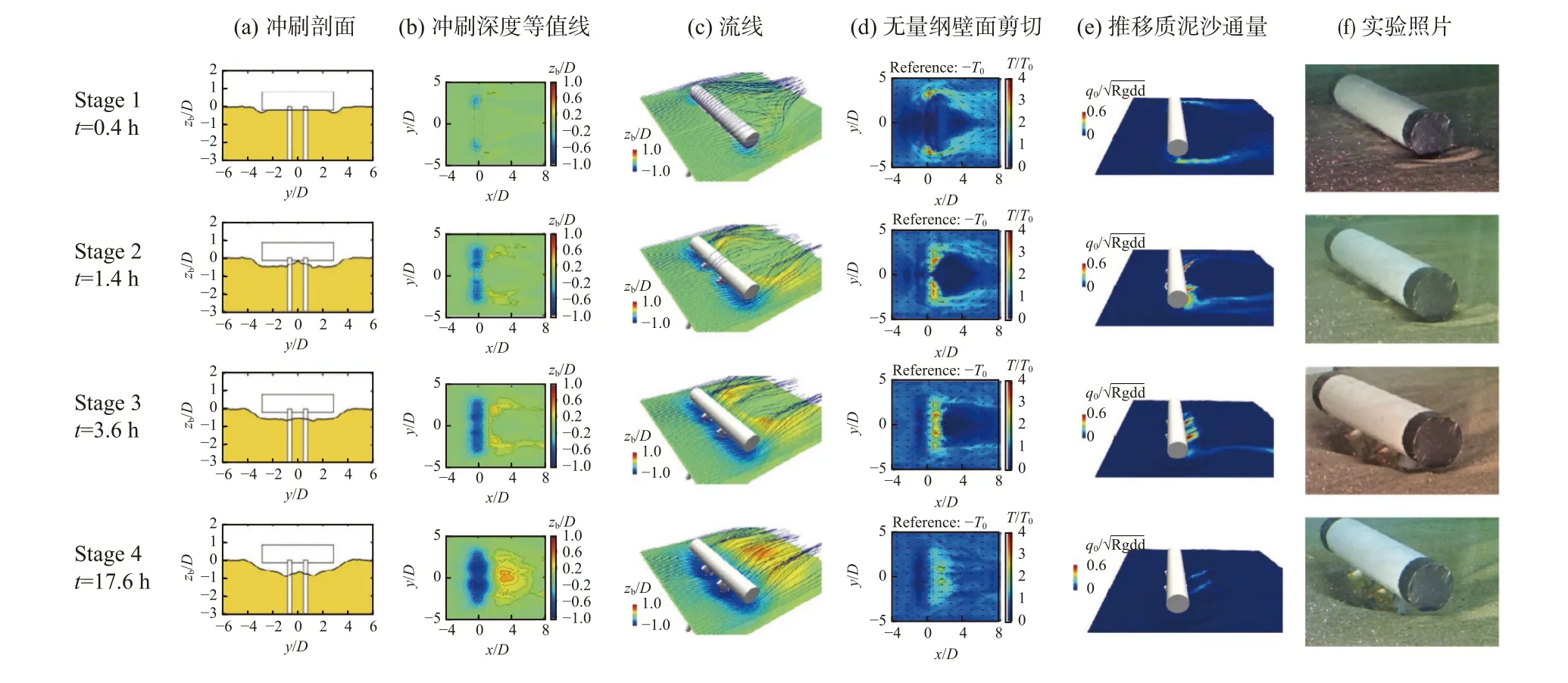
图15 IBM方法模拟的由基础支撑的水平圆柱体冲刷过程Fig.15 Simulation of the scouring processaround horizontal cylinder supported by foundations based on the IBM method

图16 不同数值模型模拟的桩基冲刷过程中上下游冲刷坑深度变化对比Fig.16 Comparison of upstream and downstream scour pit depth variation by different numerical models

值得注意的是，单相流模型仅适用于悬沙浓度较低、悬沙运动不足以对水流运动产生较大影响的情况。因此单相流模型多应用于低含沙量的非黏性泥沙输移过程的数值模拟中[65]。另外，虽然基于ALE动网格算法的单相流冲刷模型广泛地应用于局部冲刷数值模拟中，但是该模型在实际应用或者模型植入中还存在一定的问题，尤其是在基于OpenFOAM的单相流泥沙输移模型中边界条件或者求解算法的设置容易导致模拟精度不足或者求解稳定性较差等问题，存在进一步优化的空间。例如，在悬沙输移模拟中通常需要指定底边界的泥沙浓度或者泥沙通量，但是为了保证计算的稳定性，悬沙底边界通常指定在距离床面一定高度处[56]，这样会导致出现悬沙的底边界与流体底边界位置不一致的问题。部分学者[68]通过子网格算法来解决这一问题，如图17所示，计算区内使用了两套网格，一套为底部边界在壁面处的流体网格，另一套为底部边界在距离壁面一定高度的悬沙计算网格，两套网格之间除了底部边界位置不同之外，其他网格点的位置完全一致，悬沙输移模拟中所需要的流速、湍动扩散黏度等数据可通过流场网格投影到悬沙计算网格。但是Liu[134]指出，由于悬沙网格和流体网格并不共形，当网格发生拉伸或者压缩之后，对两套网格间隙处的网格处理较为困难。针对该问题Liu[134-135]提出了高/低雷诺数时适用于流体网格底边界的悬沙浓度边界条件，虽然Yang等[136]将高雷诺数的边界条件成功地应用到孤立波冲刷的数值模拟中，但是在模拟中仍然存在泥沙浓度容易越界的问题。另一方面，Liu[135]中所提出的低雷诺数的边界条件由于其计算量相对较大，在复杂地形的动网格模拟中的应用仍然较为困难。Zhou[65]和Brown[137]通过计算近底的泥沙通量来设置底边界条件，但是仍然存在边界位置不一致的问题，并且该方法对时间步长或者首层网格的最小高度均有较高的要求。此外，由于受到OpenFOAM中动网格求解算法的影响，在动网格模拟中容易产生底边界处网格被过度拉伸或者压缩等畸变问题（图18）。李金钊[138]提出了一种基于MATLAB的人工网格调整算法，该算法会扫描底边界处的网格点分布，若存在过度畸变的网格则会依照分布特征来人工调整网格点的位置，再通过OpenFOAM中的mapField工具将修正前网格的流场特征投影到修正后的计算网格上，以保证计算能够顺利进行。但是，该方法引入了过多的人工干预。另外，如何对泥沙滑移过程实现高效模拟仍然是数值模型发展中的难点问题。

图17 悬沙输移子网格算法示意图Fig.17 Schematic diagram of the sub-grid algorithm for suspended sediment transport

图18 OpenFOAM动网格模拟中的网格畸变Fig.18 Mesh distortion in OpenFOAM dynamic mesh simulations

2.2 欧拉-拉格朗日模型

欧拉-拉格朗日模型中将泥沙相视为一定数量的单个粒子，而流体相的运动则通过欧拉法求解。通过拉格朗日方法描述泥沙运动可以更好地捕捉天然泥沙的个体和群体动力学特性，而且拉格朗日模型的算法植入相对简单，同时也避免了由于对流项空间离散引起的数值耗散问题[139]。Li等[140]在OpenFOAM中植入了基于欧拉-拉格朗日算法的局部冲刷模型，并通过桩柱冲刷试验数据对模型进行了详细的验证，随后对管线局部冲刷过程开展模拟分析（图19）。结果表明在欧拉-拉格朗日模型中无需任何参数化假设即可实现对泥沙滑移过程的模拟，并且在对管线局部冲刷模拟中可以直接从平坦床面开始计算，而无需像Brørs[55]和Zhao和Cheng[58]等基于ALE动网格的单相流冲刷模型一样，在管线下方预留一定深度的初始冲刷坑。

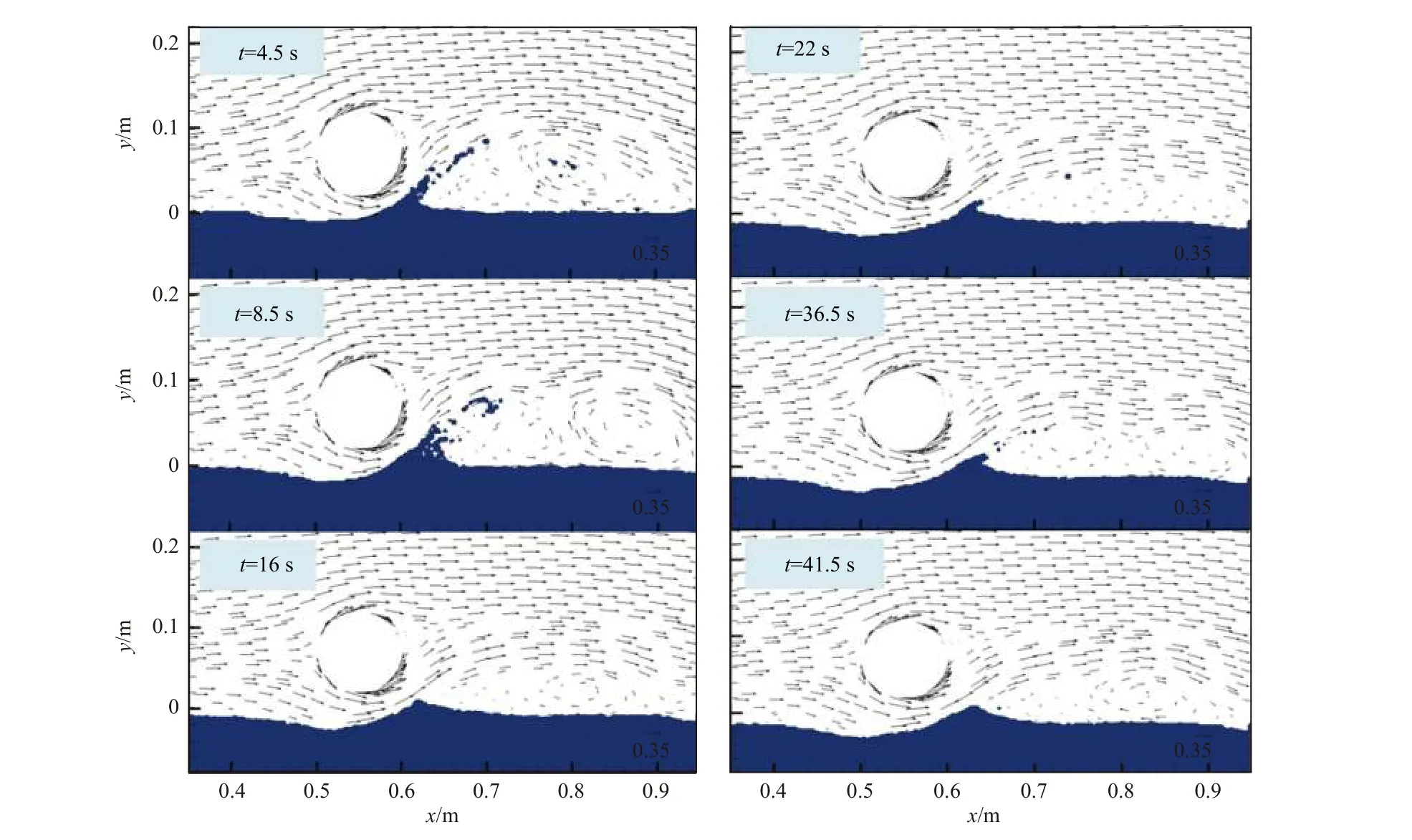
图19 基于欧拉-拉格朗日方法模拟的海底管线冲刷过程Fig.19 Simulation of thepipeline scouring process based on the Euler-Lagrangemethod

除了经典的欧拉-拉格朗日模型之外，计算流体力学-离散单元法（Computational Fluid Dynamics-Discrete Element Method，CFD-DEM）也同样被用到泥沙输移的模拟中。在CFD-DEM模型中，泥沙运动的模拟同样在拉格朗日框架下对单个颗粒进行追踪，水沙两相求解通过网格内水相体积分数和拖曳力（动量源项）进行耦合，泥沙颗粒之间的碰撞过程采用硬球模型或者软球模型模化。Sun和Xiao[141]基于OpenFOAM和LAMMPS（Large-scale Atomic/Molecular Massively Parallel Simulator）开发了开源CFD-DEM求解器“SediFoam”（图20），其中植入了一种coarse-graining方法[142-143]，可以模拟与粒径网格尺寸相似的泥沙颗粒的运动，并且该求解器也具有较高的并行计算效率，可以模拟包含颗粒数量为107量级的泥沙运动过程。另外，ANSYS FLUENT与EDEM相耦合的方法同样是工业界广泛使用的CFD-DEM模拟方法，在海洋工程中，众多学者利用该方法对泥浆泵或者输运管道中的颗粒流动开展了数值模拟研究[144-148]（图21）。

图20 基于CFD-DEM方法模拟的明渠泥沙输移Fig.20 The simulation of open channel sediment transport based on CFD-DEM method

图21 6级泵内泥浆输运流模拟Fig.21 Simulation of theslurry transport in the6-stagepump

无论是哪一种欧拉-拉格朗日模型，如今面临的首要问题都是计算量过大。虽然并行计算可以大幅度提高计算效率，但是由于模拟过程中需要捕捉每个离散粒子的运动过程，导致其计算量会远大于其他泥沙输移模型。在模拟时间步长方面，计算拉格朗日粒子运动的时间步长要小于欧拉项求解的时间步长[149]，这会导致计算成本进一步增加。因此，如何减小计算量为目前欧拉-拉格朗日模型的主要研究热点与发展趋势。除此之外，离散粒子的碰撞模型以及如何高效实现粒子捕捉同样为欧拉-拉格朗日模型的主流研究方向。

2.3 两相流欧拉模型

两相流欧拉模型中将泥沙相也视为和流体一样的连续相，并利用欧拉法同时求解泥沙与流体的运动。欧拉-欧拉模型主要由3个基本部分组成：场方程、本构方程和界面应力条件[150]。场方程为各相运动的基本控制方程，即连续性方程和动量方程。通过各相之间的本构关系和界面应力条件来实现控制方程的闭合。欧拉-欧拉模型可以不依赖经验性的悬移质或推移质输沙公式来实现对泥沙输移过程的模拟。但是在欧拉-欧拉模型中两相之间的本构关系通常十分复杂[150]，且准确模拟两相流的湍流特征较为困难[151]。另外，虽然欧拉-欧拉模型的计算量远小于欧拉-拉格朗日模型，但是由于所需求解的方程数量较多，各种应力模型较为复杂，导致其计算成本仍然较高。例如，Nagel等[152]在利用欧拉-欧拉模型开展局部冲刷模拟时发现需要花费约6 000 CPU小时来模拟10 s的桩基冲刷过程。

两相流欧拉模型一直是泥沙输移模型研究的热点，但是由于问题过于复杂，进展相对缓慢，大多数研究工作仍然局限于提出相应的数学模型[151]。目前，发展较为完善且在海洋工程中应用也较为广泛的两相流欧拉模型为Cheng等[153]基于OpenFOAM开发的两相流欧拉模型求解器“sed Foam”。该求解器基于Open-FOAM中“twoPhaseEuler Foam”求解器，修改了界面应力模型以及两相流湍流模型，同时增加了颗粒应力模型。该求解器成功地模拟了震荡流作用下近底层移输沙中瞬时床面不稳定性[153]、恒定层移输沙中的湍动能耗散，以及沉积物相雷诺应力对床面粗糙度的影响[154]（图22）。同样，该求解器已应用于海底管线冲刷[155-156]和桩基冲刷[152,157]的数值模拟研究中（如图23和图24）。但是，对比桩基冲刷模拟中单相流模型（单相流ALE和“ibScour Foam”）与两相流欧拉模型（“sed Foam”）的模拟结果发现，两相流欧拉模型对桩前后最大冲刷深度的预测上远低于单相流模型，且和实验值的误差较大（图16）。这可能是由于在两相湍流模型中各相同性的涡黏假设会导致桩前马蹄涡的强度被低估，从而造成模拟的冲刷深度较低。

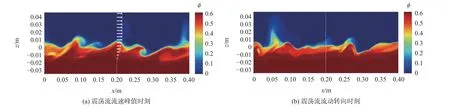
图22 sedFoam模拟的震荡流作用下近底层移输沙中床面附近泥沙浓度分布Fig.22 Sediment concentration distribution near the near-bottom bed under the effect of oscillatory flow based on sedFoam simulation

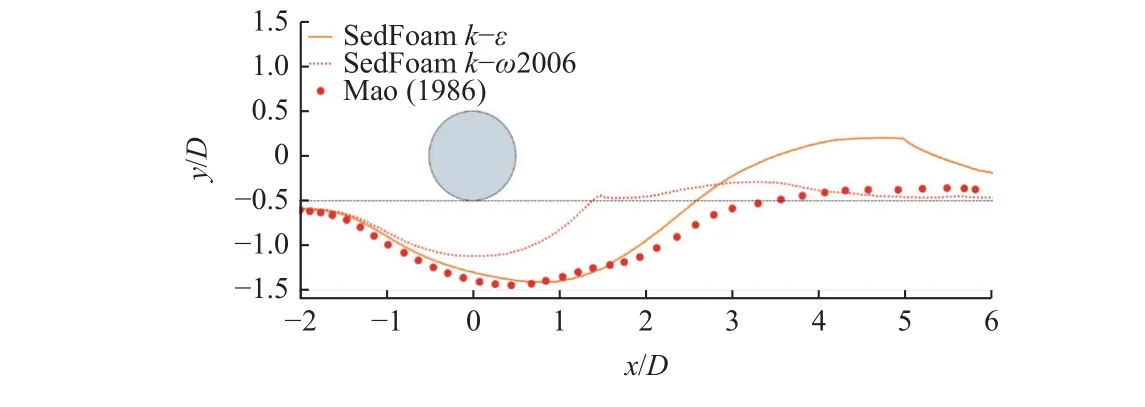
图23 不同湍流模型对sedFoam求解器管线冲刷模拟的影响Fig.23 Effect of different turbulencemodelson pipeline scour simulationswith sedFoam solver

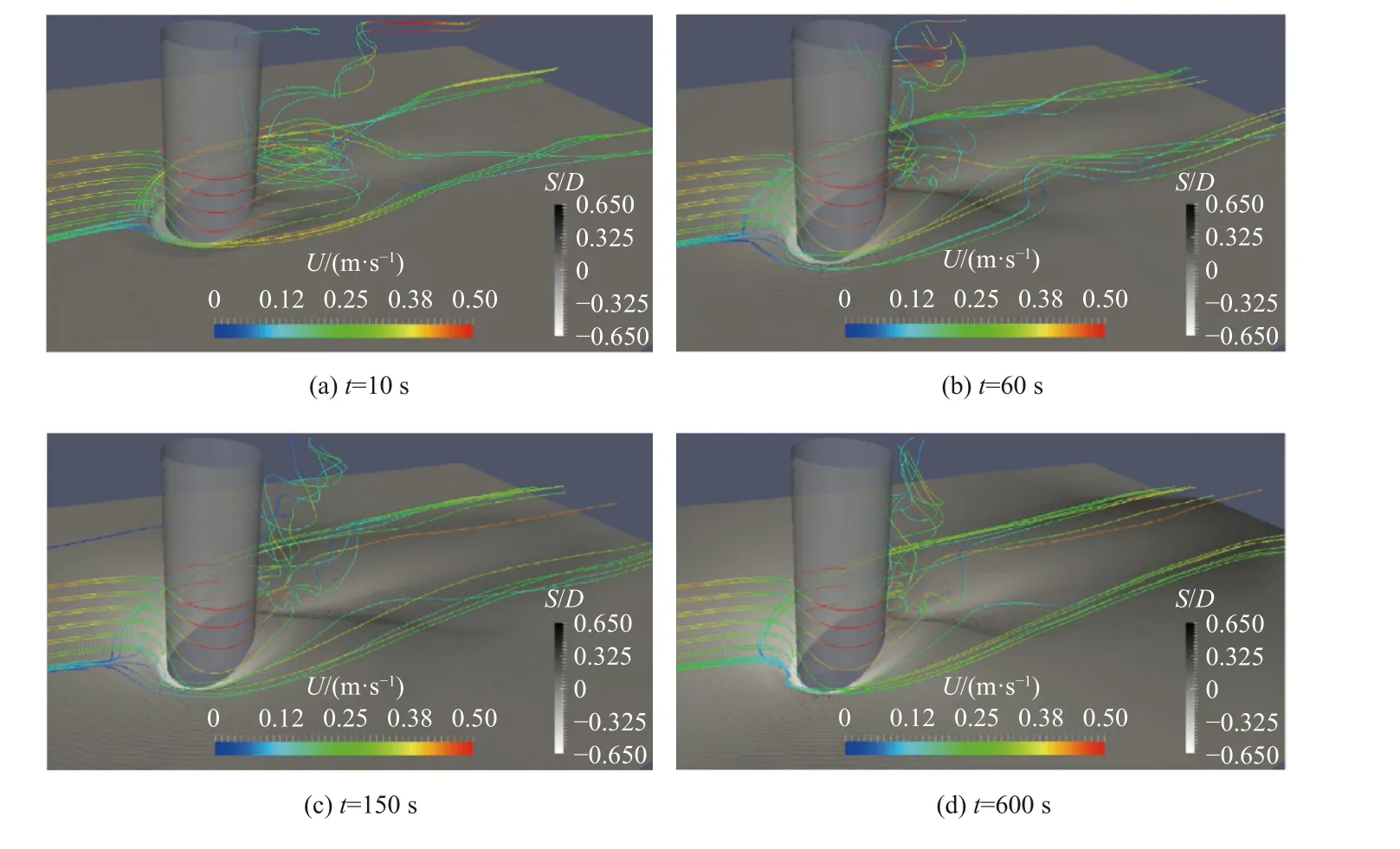
图24 基于sedFoam模拟的桩基冲刷地形变化过程及流线特征Fig.24 The bed changesand streamline characteristics during the pile scour processbased on sedFoam

2.4 两相流混合模型

两相流混合模型在一定程度上可以视为两相流欧拉模型的简化。在混合模型中将水沙混合物当作单一的连续欧拉相，混合物相的密度和速度等特征通过各相在网格内的体积分数加权计算。两相流混合模型的控制方程可通过对两相流欧拉模型中各相的控制方程推导出，将水沙各相的控制方程按照体积分数相加即得到单一混合物的连续性方程和动量方程[99]，各相体积分数的变化可以通过与单相流模型类似的对流扩散方程计算。两相流混合模型中减少了待求解方程的个数，并且在混合相中忽略了水沙两相之间的动量传递，使混合模型求解更为高效且稳定[158]。另外，混合流体的湍流闭合相对于两相流欧拉模型而言也较为简便，可通过在单相的湍流模型中引入流体密度和由密度变化引起的浮力项的修正来实现[13,159]。在混合模型中求解的是水沙混合物的运动，因此首先需要确定水沙混合物的流变特性（混合流体黏度）。由于泥沙特性较为复杂，其混合物的流变特性通常也较为复杂，如当水体中泥沙浓度较低时，水沙混合溶液仍然呈现出牛顿流体的特征，然而在泥沙浓度较高或者含有较多黏土颗粒时混合溶液则会呈现出较强的非牛顿流体特性，因此不存在统一的流变模型。常用的流变模型为Bingham模型[160]和Hershel-Bulkley模型[161]等。此外，在混合模型控制方程推导过程中会引入一个由水沙两相之间的相对运动导致的扩散应力项，需要确定两相之间的相对运动速度（飘移速度）。两相之间的相对运动通常是由两相之间的密度差异所造成的，其中泥沙沉降的影响不可忽略。但是对于不同粒径的泥沙其沉降特性差异较大，沉降速度模型也不尽相同。因此，两相流混合模型通常为一个高度特异化的数值模型，需要根据所研究的问题特性或者泥沙特性选取合适的流变模型和相对速度模型。

Mikko等[150]指出两相流混合模型一般适用于泥沙粒径较小时的悬浊液运动的模拟。Brennan[162]在OpenFOAM中植入了两相流混合模型求解器“dirftFlux Foam”，并将其应用于沉沙池中悬沙沉降的模拟研究中。近年来，Medina和Laurent[163]在“dirftFlux Foam”求解器中加入了压缩相的影响以模拟沉沙池中活性污泥的沉降过程。Le Minor等[99]利用“dirftFlux Foam”求解器模拟了单株红树林幼苗附近的局部流场以及泥沙运动特性（图25），结果表明该模型可以很好地捕捉红树林幼苗前方的马蹄涡以及后方的涡脱落过程，并且幼苗的存在会增加底床泥沙的不稳定性。此外，两相流混合模型还常与LES方法相结合应用于泥沙排放羽流的运动过程的模拟中[92,95]。

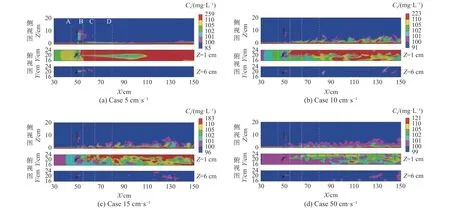
图25 不同来流速度条件下红树林幼苗后方泥沙浓度分布特征Fig.25 Characteristics of sediment concentration distribution in the back of mangroveseedlings under different inlet velocities

除了上文中提到的OpenFOAM、REFF3D和Fluent之外，Flow-3D同样是海洋工程水动力和局部冲刷模拟中广泛使用的CFD软件。从严格意义上来说，Flow-3D中的冲刷模型并不属于以上任何一种分类，而是一种类似两相流混合模型与单相流模型的混合方法。Flow-3D中的悬沙输移通过两相流混合模型中的dirft-flux方法模拟，推移质通过单相流模型中经验公式计算，而泥沙床面的变化则通过其特有的FAVOR方法（Fractional Area/Volume Obstacle Representation method）来实现。然而由于商业软件的黑箱特性，其模型中的一些细节并不透明，如尚不明晰在悬沙输移模型中是否考虑了混合流体的流变特性。相比于其他软件，Flow-3D的优点是界面友好、网格生成难度较低。因此众多学者利用Flow-3D对桩基冲刷[164-166]或者管线冲刷[167-168]过程开展数值模拟研究（图26）。

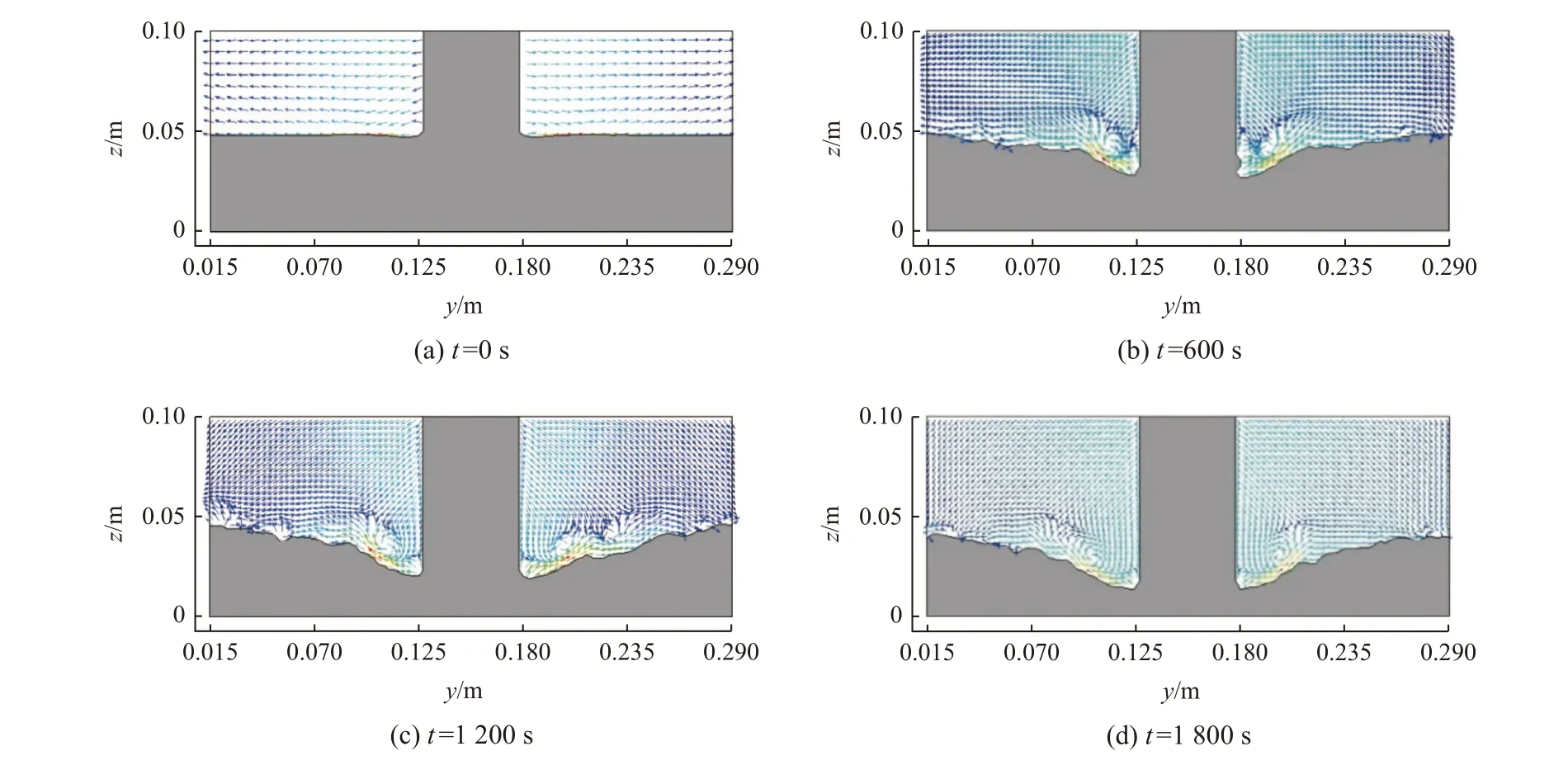
图26 Flow3D模拟的桩基冲刷过程及流速场分布特征Fig.26 Characteristics of pilescour process and flow field based on Flow3D simulation

3 结语

本文通过分析海岸、海洋工程中水动力及泥沙输移过程CFD模拟的现有相关研究，得到下述结论。

1）在不同湍流模拟方法中，DNS方法以及LES方法由于其过高的计算量在现阶段无法应用于对海洋与海岸工程中高雷诺数的复杂流动的模拟中，而RANS方法无法准确地解析流场中的湍流波动特征。相比而言，RNASLES混合方法有望为高雷诺数条件下复杂流动的精细化模拟提供高效的模拟方法。

2）由于泥沙输移问题的复杂性，目前尚不存在可用于模拟所有泥沙输移问题的统一数学模型。在对局部冲刷问题的模拟中单相流模型的应用最为广泛，具有较高的模拟精度与计算效率。两相流欧拉模型和两相流混合模型则更适合应用于高浓度层移输沙或者黏性泥沙输移过程的模拟中，而对于局部冲刷问题的模拟精度及效率均低于单相流模型。进一步发展并完整两相湍流模型有助于提高两相流泥沙输移模型的模拟精度。

3）超级计算机技术的发展极大地提高了数值模拟的计算效率。因此，结合RNASLES混合方法进一步发展包含气、液、固多相的全级配泥沙输移模型，可为复杂因素影响下泥沙输移过程的精细化模拟提供必要技术支撑。