基于改进K-means聚类算法的上市公司信用风险评估研究

赵 衡，彭 铃，李云飞

(西华师范大学 数学与信息学院，四川 南充 637009)

0 引言

近年来随着我国金融市场的逐渐开放，引入外资银行以及国内金融机制的改革，我国金融市场迅速发展，市场规模也不断成长.2020中国金融学会学术年会披露，我国上市公司数已达4100家，上市公司总市值超过79万亿元，位居全球第三.这也说明我国资本市场目前最急迫的问题已不再是快速扩大上市公司数量，接下来面临的将是如何提高上市公司质量的问题，要确保我国资本市场未来可持续且平稳健康的发展.我国上市公司目前面临亟待解决的问题有上市公司管理制度不规范、信息披露不充分、财务信息不准确、退市制度不完善、券商参与了上市公司造假行为等，这些都将影响我国经济健康发展和投资者的利益.因此，探索上市公司信用评级方法至关重要，为了提高上市公司质量，应建设规范、透明、开放、有活力、有韧性的资本市场.

早期比较流行的信用风险评估方法是专家基于企业提供的材料，利用个人经验以及专业技能，对企业信用进行评估并衡量其风险，即5C、5W、5P方法以及Alexander Wole提出的沃尔评分法与杜邦财务分析体系[1].然而，此类方法对评估者的专业知识要求高而且主观性强，属于定性分析.随着市场经济的发展以及20世纪90年代信息技术不断发展与成熟，人工智能方法在信用风险评估中应运而生，机器学习模型被引入到信用风险评估研究中.例如，Makowsik[2]首次在信用评估中应用决策树模型；Tae等[3]提出用决策树模型建立基于经济正常与经济危机两种情况下的经济破产预测模型；吴世农等[4]通过资产变现力、负债状况、资产使用效率和盈利能力4个方面，建立以线性判定分析法为主的企业破产预测模型，研究结果显示此模型对破产企业和非破产企业均具有较高的预测能力；Odom[5]以Altman建立Z值分析模型时选取的5个财务指标作为输入变量，构建了神经网络模型，研究对象为128家破产和非破产企业，结果表明神经网络模型对非破产企业预测的准确率高于破产企业；周首华等[6]基于改进的Z评分模型，建立了财务预测模型——F分数模式，并用Compustat PC Plus会计资料库中的4160家公司验证，其准确率达到70%；Gao等[7]通过对上市公司2012-2014年财务状况与股价等相关数据的分析，构建的AHP与KMV-Merton模型，并验证其合理性，拓宽结果可靠性思路，探讨如何加强我国SEMs信用评级体系；Guo等[8]提出了一种基于BP神经网络的贷款风险评估算法，爬取2015—2019年P2P借贷平台数据，并采用Logistic回归与BP神经网络进行比较，发现BP神经网络的算法优于传统Logistic回归算法；袁宇等[9]首先采用网络爬虫技术获取80家健康平台数据，利用K-means聚类方法构建P2P网贷平台信用风险预警模型，合理预测平台风险情况；孙剑斌等[10]运用CHAID决策树和BP神经网络模型分别对555家上市公司进行预测，发现BP神经网络模型预测结果较好；仵晓溪等[11]运用优化后的基于熵权-FCM模型和传统FCM模型对50家上市公司进行信用风险评估研究，发现优化后的模型对上市公司的信用风险级别划分更加合理有效.

聚类分析属于无监督机器学习方法，它基于物以类聚原理，分析和探索事物的内在联系和本质[12].聚类算法不需要对样本数据进行标记，可以从样本数据出发，根据样本点自身的特征，自动进行分类；聚类分析过程是一种根据相似性原理，将样本数据分类到不同的类或者簇，属于同一簇中的对象相似度高，而不同簇间的对象有相异性.如王赛芳等[13]针对传统K-means聚类算法对初始中心和孤立点的问题，提出一种基于密度选取初始聚类中心的方法，利用随机产生的三组实验数据验证改进的K-means聚类算法的效果，发现改进后的算法能产生高质量的聚类结果；谢娟英等[12]针对传统K-means聚类算法随机选取初始聚类中心，发现这样容易导致聚类结果不稳定，且优化初始聚类中心需要人为选择参数等缺点.于是基于样本空间紧密度，提出利用最小方差优化初始聚类中心的K-means算法，发现改进的K-means聚类算法使得聚类结果稳定且抗噪音效果强；王菲菲等[14]对于K-means聚类算法初始中心选取敏感以及需要先给定初始聚类中心这两个方面的缺点，提出一种二分类思想和BWP指标改进算法，发现改进的算法具有更高的有效性和稳健性；马克勤等[15]利用加权密度法选取初始聚类中心点时，为了减少离群点的影响，提出一种基于最大最小距离和加权密度的K-means聚类算法，最后在人工数据集和UCI数据库验证，发现改进的算法增强了稳定性.对于上市公司的研究，蒲永平[16]采用系统聚类和快速聚类对150家公司的数据进行聚类，最后用散点图对其进行了准确性验证.

但是传统的K-means聚类算法也存在一定的缺陷：聚类指标间的冗余性与重要性差异会影响聚类的效果、最佳聚类数不易确定、聚类的准确性及稳定性易受初始聚类中心选取的影响等.本文针对传统的K-means聚类算法在确定初始聚类中心时具有随机性的缺点，基于密度和权重对传统K-means聚类算法进行改进，并对上市公司的信用风险评估问题进行研究.

1 K-means聚类算法

1.1 传统K-means聚类算法

K-means聚类算法是一种应用广泛且基于划分的聚类算法.传统的K-means聚类算法是将误差平方和作为判断聚类效果的准则函数.K-means聚类算法是将含有R个样本的集合划分为互不相交的K个簇，属于同一个簇的样本相似度较高，而不同类簇之间的样本相似度较低.K-means聚类算法的基本思路是：首先在一个含有R个样本的集合中随机选取K个样本作为初始聚类中心，根据每个样本到K个中心的欧氏距离，将样本分配到最相似的聚类中心，从而得到互不相交的K个簇；重新计算K个簇的新中心，然后再根据欧氏距离原理将R个样本分配到最相似的类簇.不断重复迭代此过程，直到K个类簇中心不再改变，从而得到原始集合的互不相交的K个稳定的类簇.

1.2 基于密度和权重改进的K-means聚类算法

传统的K-means聚类算法对初始聚类中心的确定具有随机性，同时也可能会选到孤立点或噪声点，这样可能会导致聚类结果与样本数据集的真实分布不一致，得不到正确的聚类结果.已有学者针对传统K-means聚类算法随机选择初始聚类中心的缺点，提出根据样本数据的紧密程度选择聚类中心，从而可以避免初始聚类中心不稳定和需要人为给定参数的缺陷，保证聚类结果的客观性和稳定性[17-19].然而对于孤立点或噪声点的缺陷，陈小雪等[20]和王子龙等[21]提出一种基于距离和样本权重改进的K-means聚类算法，采用维度加权的欧式距离，从而减少异常点的影响.尽管近年来已有学者针对传统K-means聚类算法随机选取初始聚类中心，容易造成聚类结果不稳定的缺陷，提出了一些优化初始聚类中心选择的方法，使得聚类的结果更加稳定，然而却忽视了样本数据中异常点的影响.因此本文根据样本空间的紧密程度最高(即方差最小)的原则，再采用引入权重后的平均距离作为半径，选取K个位于不同区域的初始聚类中心，提出了结合样本密度和权重改进的K-means聚类算法.根据方差最小的原则优化初始聚类中心的选择可以避免其随机性，同时初始聚类中心从相距较远的簇中选取从而避免其位于同一簇中，引入权重是为了减少离群点对聚类结果的影响.

假设给定的待聚类数据集M={x1,x2,x3,…,xn}，且每个样本点均为m维，表示为xi={xi1,xi2,xi3,…,xim}(i=1,2,…,n).

定义1[20]计算距离时样本点不同维度数据的权值计算式为：

(1)

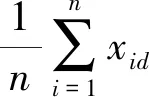
定义2[12]样本点xi，xj之间的欧式距离为：

(2)

定义3样本点xi到所有样本点的平均值距离为：

(3)

定义4[12]样本点xi的方差为：

(4)

定义5样本数据点平均欧氏距离为：

(5)

定义6[12]聚类误差平方为：

(6)

1.3 基本思路

参考谢娟英等[12]的研究方法，以方差衡量样本点的密度，根据密度最大，以样本空间加权后的距离的平均值作为半径，选取K个位于不同区域且误差平方和最小的样本点作为初始聚类中心.本文考虑基于样本空间的紧密程度和权重选取初始聚类中心.若想要达到聚类收敛的效果，首先通过式(4)计算样本点数据的方差，找到密度最大的样本点为初始聚类中心，以样本数据点赋予权重距离的平均值为半径，位于此区域的样本数据点构成集合M1；在M-M1中选取方差最小的样本点，以余下所有样本数据点的赋予权重距离的平均值为半径，且处于该区域的样本数据点构成集合M2；不断重复上述步骤，直到将待聚类数据集M划分为K个位于不同区域的集合；再将每一个集合M1,M2,…,MK的均值作为该集合新的聚类中心；最后再由式(6)计算聚类的误差平方和.

1.4 基本步骤

输入：数据集M={x1,x2,x3,…,xn}，分类数K.

输出：K个聚类簇.

1.4.1 确定初始聚类中心：

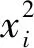
M2={d(xj,xi2)cmean,j=1,2,…,n}.

(3)重复上述步骤，直到找到K个互不相交的集合.

1.4.2 构造初始划分

(1)根据式(2)得到每个样本点到选取的K个初始聚类中心的欧式距离，再把样本点划分到最近的类中，构成初始划分;

(2)计算初始划分每一类的均值，并作为该类的新中心;

(3)由式(6)计算聚类结果的误差平方和.

1.4.3 迭代更新聚类

(1)根据上次聚类得到新的聚类中心，由式(2)计算样本数据点到新中心的欧式距离并分配到最近的类;

(2)计算每一类的均值，并作为该类的新中心;

(3)由式(6)计算聚类结果的误差平方和;

(4)将此结果与上次聚类的误差平方和进行比较，若E′-E10-10，则满足聚类中心不再改变，迭代终止，输出聚类结果；否则，继续上述步骤，直到聚类结果收敛.

2 数据来源和指标筛选

2.1 数据来源

本文从网易网站(http://quotes.money.163.com/stock)选取上市公司的财务数据，包括偿还能力、成长能力、盈利能力、营运能力.从以上四个维度选取能够诠释上市公司运营状况的财务指标，构建信用风险评估体系.如果上市公司出现违约或违规状况通常会被特别处理，即对该公司实施ST制度.无论是银行或是投资者均会优先考虑“非ST”上市公司，现从网易财经股票网站中随机选取了沪、深两市50家“非ST”企业作为评估对象，并截取其2020年的年报数据，均包含四个维度，一共27个财务指标，具体如表1所示.

2.2 指标筛选

有诸多因素会影响上市公司信用风险的评估结果.因此，指标的选取要遵循合理性、全面性及客观性等原则，判断选取的指标是否科学合理，会对所选取的上市公司评估结果产生影响.由于本文选取的50家上市公司2020年的27个财务指标中，有部分指标所表达的经济学信息含义相同，也即指标之间具有相关性，本文首先采用因子分析法对选取的27个指标进行降维处理，以便筛选出最有效的财务指标来综合反映各公司的财务状况.根据KMO和Bartlett球体检验结果分别为0.703、0，而理论上KMO值大于0.5且Bartlett球体检验的显著性P值小于0.05就适合进行因子分析.因此，本文选取的27个财务指标可以通过因子分析法进行降维处理.

本文运用数据分析软件SPSS26对27个财务指标进行分析，在因子分析法中选择最大方差法对因子进行旋转，从而可以提取到6个公共因子，且公共因子累计贡献率为78.72%.所提取到的6个公因子基本上可以覆盖所选取的研究对象的绝大部分信息，通过Kaiser正态化最大方差法，旋转在9次迭代后收敛，旋转成分矩阵如表2所示.第一类公共因子F1，其中n18、n19、n20三个指标具有较大载荷量，分别为：0.806、0.920、0.926；第二类公共因子F2，其中n8、n9、n6、n25四个指标具有较大载荷量，

表1 财务指标体系

分别为：0.878、0.848、0.847、0.800；第三类公共因子F3，其中n27、n26、n5三个指标上具有较大载荷量，分别为：0.905、0.796、0.729；第四类公共因子F4，n17、n10、n16三个指标具有较大载荷量，分别为：0.756、0.731、0.704；第五类公共因子F5，其中n4、n14两个指标具有较大载荷量，分别为：0.888、0.750；第六类公共因子F6，其中n22、n21两个指标上具有较大载荷量，分别为：0.679、0.588.为检验选取的六大类公共因子的合理性，再对每个指标大类做KMO和Bartlett检验，根据KMO大于0.5且Bartlett球体检验显著性P小于0.05，选择载荷量最大的一项作为信用风险评估指标.结果显示，只有第一类公共因子到第四类公共因子通过检验.

综上所述，经过因子分析法分析发现对于第五类和第六类公共因子均保留，从而对指标进行降维处理后，剔除19个指标，余下8个指标为n4、n8、n10、n14、n20、n21、n22、n27.

表2 旋转后的成分矩阵a

3 算例仿真分析

3.1 标准化处理

本文对上市公司财务指标进行因子分析后，选取了8个财务指标，但不同财务指标之间单位不同，如基本每股收益(元)、销售净利润(%)、固定资产周转率(次)，且三个指标之间单位存在计量与数量级的差异.所以为了消除各项指标之间量纲不同的影响，需要对数据进行标准化处理.常见的数据标准化方法有：Z-score标准化、最大-最小标准化、按小数定标标准化.由于财务指标有正向指标、中性指标和逆向指标之分，故本文对数据进行标准化处理时，采用最大—最小标准化方法.

正向指标标准化：

逆向指标标准化：

中性指标标准化：

式中，xij'代表标准化后的值；xij表示第i个上市公司的第j个财务指标数据值；n代表上市公司总数；q为适中指且通常为1[11].

3.2 K-means聚类

为了进一步说明本文改进的算法性能有所提高，分别采用传统K-means聚类算法、最小方差聚类算法和本文算法在UCI机器学习数据库上进行验证[22].

按照信用风险级别将上市公司分以下三类：低风险、中风险、高风险.本文利用python编写传统K-means聚类、最小方差K-means聚类和本文改进的K-means聚类算法的程序，将50家上市公司的27个财务指标，经因子分析法降维处理与标准化处理后筛选出的8个财务指标数据导入编写好的程序，最后比较三个程序迭代终止时的误差平方和，依次为19.473 46、9.547 96、9.529 45.验证结果显示，本文改进的算法误差平方和有所提高.

基于密度和权重改进的K-means聚类迭代终止，将本文选择的50家上市公司聚为三类，其中低风险公司有1家，中风险公司有24家，高风险公司有25家，具体的评级结果如表3所示.最后将本文聚类的评级结果与仵晓溪等[11]的研究结果进行比较，结果表明本文的信用风险等级划分结果与其基本吻合.

4 结论及建议

4.1 结论

本文从网易网站选取50家上市公司2020年财务数据，根据样本的紧密程度最高(即方差最小)的原则和引入权重后的平均距离作为半径，选取K个位于不同区域的初始聚类中心，提出运用密度和权重改进的K-means聚类算法对上市公司进行信用风险评估研究，最终比较传统的K-means聚类算法、最小方差K-means聚类算法以及本文改进的K-means聚类算法迭代终止时的误差平方和.研究结果表明，本文改进的算法误差平方和最小为9.529 45，并且将选取的研究对象聚类为三类，其中1家属于低风险，24家属于中风险，25家属于高风险.

4.2 建议

目前，根据我国金融市场发展现状，提高上市公司质量是首要问题.因此，需要构建合理有效的信用风险评估模型，探索研究上市公司信用风险评估问题.其一，针对指标的选取方面.首先要考虑指标的全面性、客观性以及具有代表性，其次筛选出能够真实有效反映我国上市公司现状的指标体系；其二，本文针对选取的50家上市公司采用密度和权重改进的K-means聚类算法构建的上市公司信用风险评估模型进行三分类研究，从而投资者可以考虑从低风险和中风险的25家上市公司选择风险较低的公司进行投资，同时在保证降低投资风险的基础上争

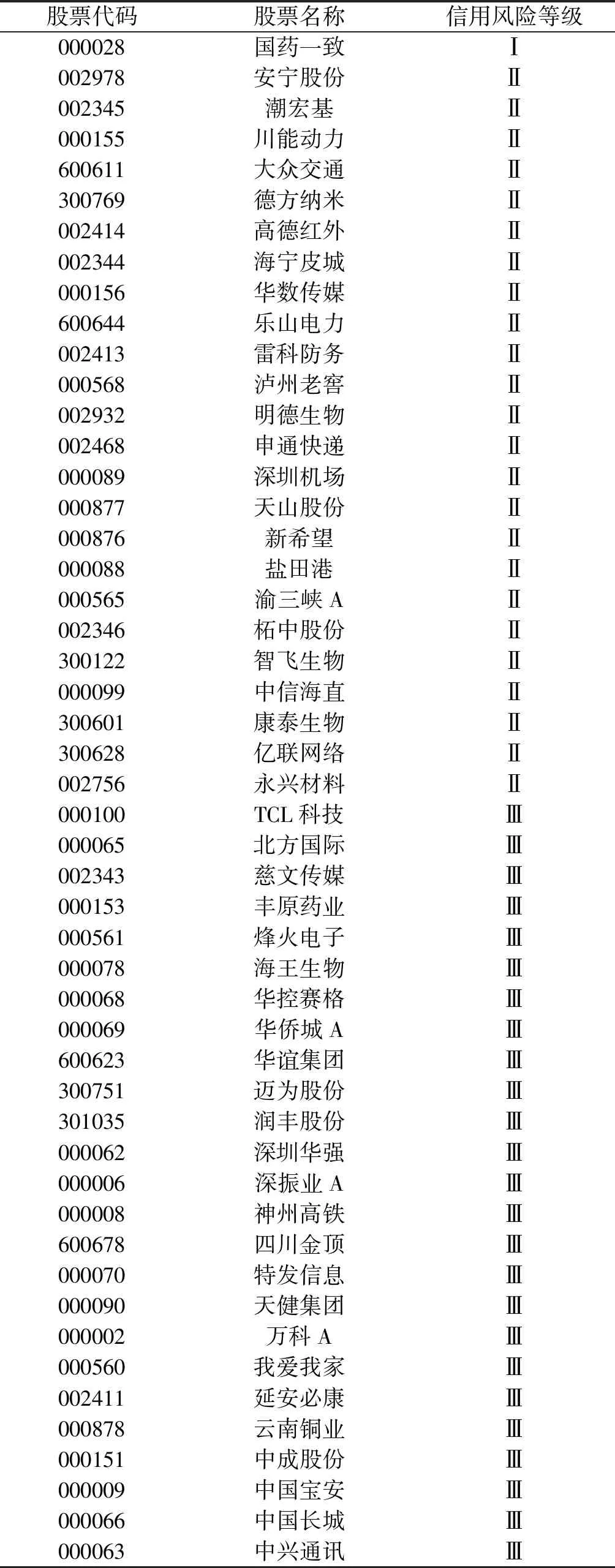
表3 评级结果

取能够获得更大收益.此外，公司管理者可以根据信用风险评级结果制定公司未来发展的策略，比如针对划为高风险等级的上市公司，管理者可以从公司股权分配、各职能部门工作是否协调等多方面进行考虑.所以构建合理有效的上市公司信用风险评估模型有益于投资者的投资决策和有利于上市公司更好地发展.