含孔边裂纹钢板的轴心受压试验和模拟分析

陈惠全，黄云海，张炯

（1.五邑大学 土木建筑学院，广东 江门 529020；2.广东华路交通科技有限公司，广东 广州 510000）

钢薄板广泛应用于建筑及桥梁工程中，在实际工程中，由于各种需要不可避免地会对薄板进行开孔[1-3]，比如检修孔、螺栓孔、排水孔、管线孔和结构孔等.开孔后的薄板在各种周期性荷载（比如疲劳荷载）作用下容易产生裂纹，进而严重影响薄板的力学性能.而一旦钢板的孔边出现裂纹，在某些偶然荷载如地震、台风、爆炸和撞击等作用下，钢板承受压应力将出现屈曲问题[4-5].因此研究含孔边裂纹钢板在轴心受压作用下的屈曲性能，对保证结构安全有很重要的工程意义.

对屈曲性能的研究最早可以追溯到 18 世纪中叶欧拉和拉格朗日对压杆屈曲的研究，但是仅限于线性问题.几何非线性和物理非线性的屈曲理论在1900 至1950 年间得到了蓬勃发展.到了20 世纪下半叶，弹性稳定理论经过半个多世纪的发展取得了许多标志性成果.在20 世纪末期，随着计算手段和理论方法的发展，屈曲性能的研究空间逐渐被拓宽.近些年，数值方法和与之相应的商业软件逐渐走向多样化和成熟化，如今的数值分析软件已经可以在计算中同时考虑复杂耦合荷载、初始几何缺陷和非线性变形等因素的影响[6-7].在此基础上，越来越多的学者开始关心含孔或裂纹薄板的屈曲和后屈曲问题.Zuxing Pan 等[8]基于Muskhelishvili 复变量公式和Raleigh-Ritz 能量法提出了一种改进的混合半解析法，用于计算具有中心直穿厚裂纹的轴压薄板的弹性屈曲荷载，文献研究了不同边界条件下裂纹长度和板的长宽比对裂纹扩展的影响，结果表明：基于精准的非均匀面内应力分布，比现有的几种基于均匀面内应力分布的分析方法更准确.Mohammad Hossein Taher[9]采用试验和扩展有限元法研究了裂纹长度和裂纹位置对单裂纹薄板屈曲稳定性的影响，对含偏心裂纹的铝板进行了单轴压缩试验，并得出了相关结论.虽然Mohammad Hossein Taher 在前人的基础上增加了夹具紧固夹条的高度，实现了更大的夹紧力，但是这两种夹具都仅能对上下边缘提供加载条件，对于侧边无法提供有效的约束.

因此本文将采用试验和有限元的方法，对含孔边裂纹的钢板在轴心受压下的屈曲性能开展研究，以探索有效准确评估含孔边裂纹板件受压稳定承载力的方法，并拟合出屈曲系数经验公式.

1 含孔边裂纹钢板的轴心受压性能试验

1.1 试验介绍

本次钢板压缩试验在 SANS 万能试验机上进行.试验件采用边长200 mm、厚度1.4 mm 的正方形钢薄板.钢板的圆孔和裂纹采用迪能激光切割机进行相应的切割.本文对钢板含有单边不同形式的孔边裂纹情况开展研究，具体的裂纹形式如图1 所示.实验中薄板的上边缘固定、下边缘移动，采用位移控制进行轴心受压，试验固定加载速率为5 mm/min，并通过夹具的调整实现简支和固支的约束边界条件.

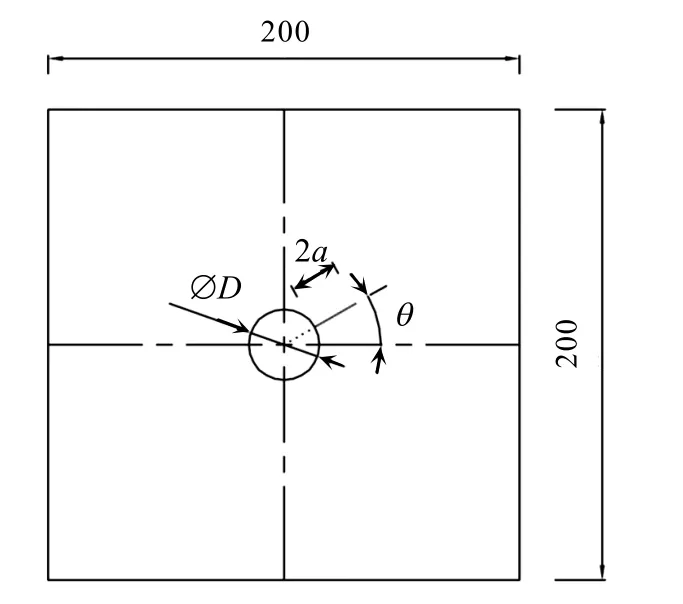
图1 含孔边裂纹板参数化模型

1.2 试验模型说明

本试验对不同孔径、不同裂纹长度和不同裂纹倾角的含孔边裂纹薄板的屈曲承载力和极限承载力进行了研究.薄板在竖直方向受压缩荷载作用，边界条件分别为C-S 和S-S，其中C-S为下端固支上端简支，S-S 为上下端简支，两种边界下的侧边均为自由边，如图2 所示.

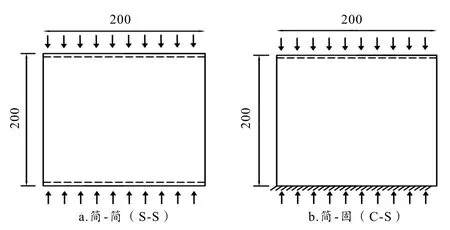
图2 模型受力及边界条件示意图

1.3 试验测试方式和加载速率

试验数据的测量和采集由SANS 万能试验机自动记录完成，测量数据主要为位移和反力.加载方式如图3 所示，加载边为钢板上下边缘，其中下边缘可移动，采用位移控制进行轴向压缩试验，试验固定加载速率为5 mm/min.

图3 加载中的钢板

1.4 试验结果

在实验中，随着薄板下边缘位移的增加，薄板中部的挠度逐渐增加，并达到极限荷载失去承载力，典型的失效形式如图4 所示.典型的位移-荷载曲线如图5 所示.

图4 典型的失效形式

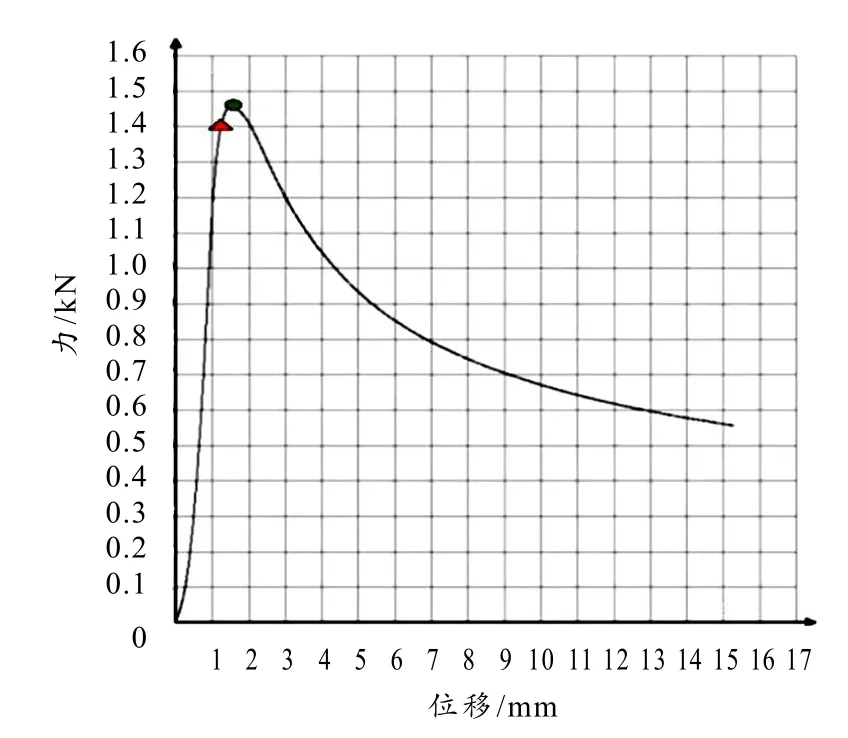
图5 位移-荷载曲线

从图5 可以看出，随着荷载的不断增加，位移-荷载曲线首先达到初始屈曲点（红色三角形点），在该过程中钢板的两个自由边的挠度并无明显增加.随着荷载的继续增加，位移-荷载曲线进入非线性段，随着位移的增加，薄板承载力稍有提升，并达到极限荷载（绿色圆形点），此时自由边挠度快速增加.随后位移-荷载曲线的迅速下降，此后试件完全丧失承载力.

1.5 试验结果分析

含孔边裂纹薄板在受压时薄弱区域在挠度较大的中部，若薄弱区域内出现裂纹，则裂纹的长度和角度将对极限荷载造成较大影响.为了探究单边裂纹长度和裂纹倾角对薄板屈曲荷载的影响，对54 个含单边裂纹的开孔板进行试验，结果如表1 所示，结果分析如图6 所示.

表1 单边裂纹板试验值

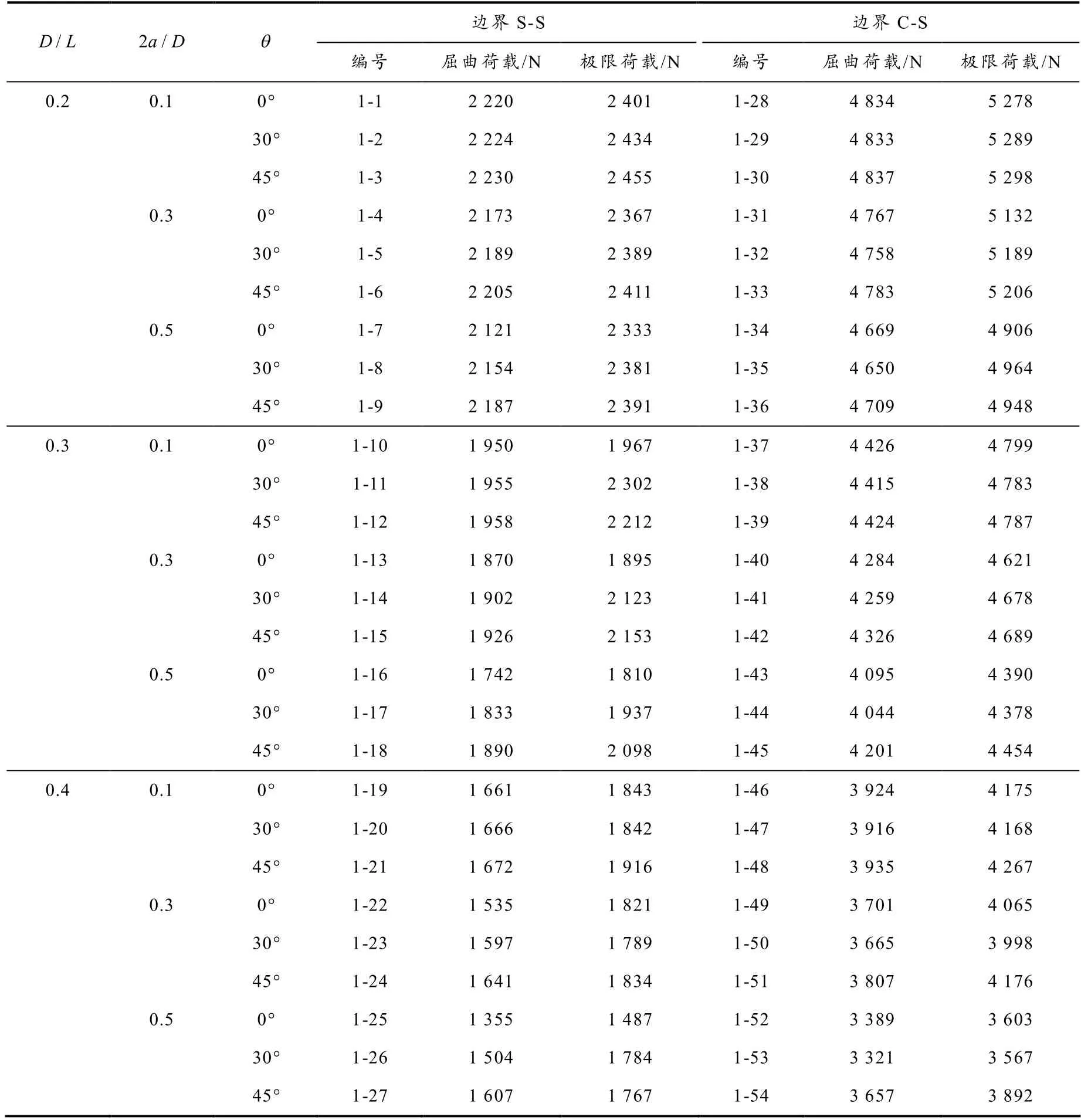
（续表1）

从图6 可以看出：1）在C-S 和S-S 边界条件下，稳定极限荷载随着裂纹长度比的增加而下降，当裂纹长度比较小时裂纹倾角对极限荷载影响较小，但是随着裂纹长度比的增加裂纹倾角的影响开始凸显；2）含孔边裂纹薄板在C-S 边界条件下的极限荷载明显大于S-S 边界条件下的极限荷载；3）在C-S 边界条件下，含孔边裂纹板的极限荷载对30°至45°的裂纹倾角变化比较敏感，而在S-S边界条件下，含孔边裂纹板的极限荷载对0°至30°的裂纹倾角变化比较敏感.

由图6-a 可见：1）D= 40 mm、θ=0°的板，裂纹长度比从0.1 增加到0.5，含孔边裂纹钢板比不含裂纹开孔板的极限承载力分别下降了1.3%、4%和8.3%；2）裂纹长度比一定时，θ=45°与θ=30°极限承载力相差不大，但与θ=0°相差较大.

由图6-b 可见：1）在C-S 边界下，D= 80 mm、θ=0°的板，裂纹长度比从0.1 增加到0.5，含孔边裂纹钢板比不含裂纹开孔板的极限承载力分别下降了4.4%、6.9%和17.5%；当θ=45°时，随着裂纹长度比从0.1 增长到0.5，其极限承载力与不含裂纹开孔板的极限承载力下降分别为2.3%、4.4%和10.8%；2）D= 80 mm，当裂纹长度比为0.5 时，θ=30°与θ=0°、θ=45°的极限承载力的差率分别为：1%和9.1%，说明θ=45°与其他两个角度极限承载力相差较大.

由图6-c 可见：1）D= 40 mm、θ=0°的板，裂纹长度比从0.1 增加到0.5，含孔边裂纹钢板比不含裂纹开孔板的极限承载力分别下降了2%、3.4%和4.77%；2）当裂纹的长度比为0.5 时，θ=45°与θ=30°极限承载力相差不大，但与θ=0°相差大.

由图6-d 可见：1）D= 80 mm、θ=0°的板，裂纹长度比从0.1 增加到0.5，含孔边裂纹钢板比不含裂纹开孔板的极限承载力分别下降了4.1%、5.3%和22.6%；2）当θ=45°时，随着裂纹长度比从0.1 增长到0.5，其极限承载力的下降分别为0.3%、4.5%和8%.

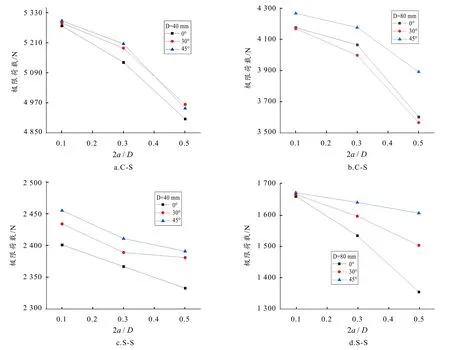
图6 裂纹长度比、裂纹倾角和孔径对极限荷载的影响

2 含孔边裂纹板轴心受压性能的有限元验证

由于钢板的屈曲荷载与裂纹参数、边界条件和开孔率等各种因素相关，因此本文采用有限元软件ABAQUS 研究各种参数对钢板的屈曲荷载的影响.在研究各种参数的具体影响之前，首先对有限元方法的有效性进行验证.

采用有限元方法对实验中的含孔边裂纹板的轴向压缩进行模拟，在有限元中，孔边的裂纹通过ABAQUS 中的Interaction 模块设置和生成，分析中采用4 节点减缩积单元[10].

在分析中，薄板的上边缘的边界条件分为固支和简支，下边缘的边界条件分为固支和简支，典型实例的边界条件、网格划分和计算结果（一阶屈曲模态）如图7 所示.

图7 典型的含孔边裂纹板的有限元模型

对C-S 单孔单裂纹板在不同裂纹长度比、倾角及孔径下的薄板屈曲承载力进行有限元模拟，并与实验结果进行对比，其结果如表2 所示.

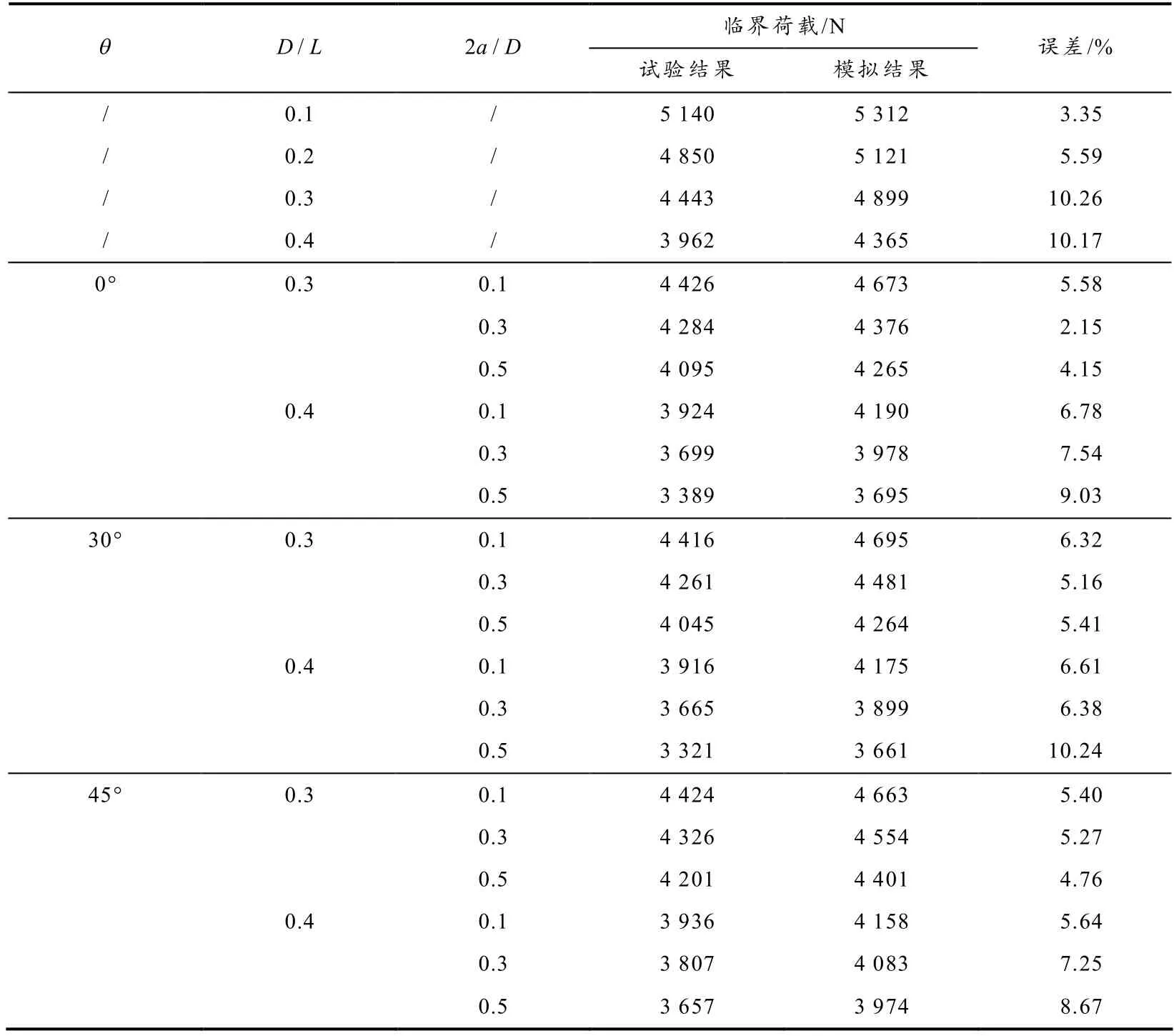
表2 有限元结果与试验结果对比

从表2 可以看出，极个别情况下，有限元分析（模拟结果）和试验结果的误差为10.26%，这是因为在有限元分析中，没有考虑薄板因加工、运输等造成的初始挠度，以及几何不完整等因素对薄板承载力的影响.此外，实验过程中夹具的对中和边界条件的实现与理想状态也存在一定的误差.除此之外，大部分误差均在6.44%左右，误差在允许的范围内，说明有限元分析结果与试验结果有较好的吻合.

3 含孔边裂纹板轴心受压的临界屈曲荷载的影响因素分析

下面通过有限元方法对裂纹参数、边界条件和开孔率等因素对钢板的屈曲承载力的影响进行分析，以期得到含孔边裂纹钢板屈曲系数经验公式，方便工程应用.

3.1 裂纹长度比对屈曲荷载的影响

在有限元中取薄板长宽为200 mm，厚度为1.4 mm，孔的直径80 mm，裂纹长度比分别取0.1、0.2、0.3、0.4、0.5、0.6 和0.7，裂纹倾斜角分别取0°、30°、45°、60°和90°，边界条件分别为S-S 和C-S，通过有限元分析得到相应的屈曲荷载，如图8 所示.

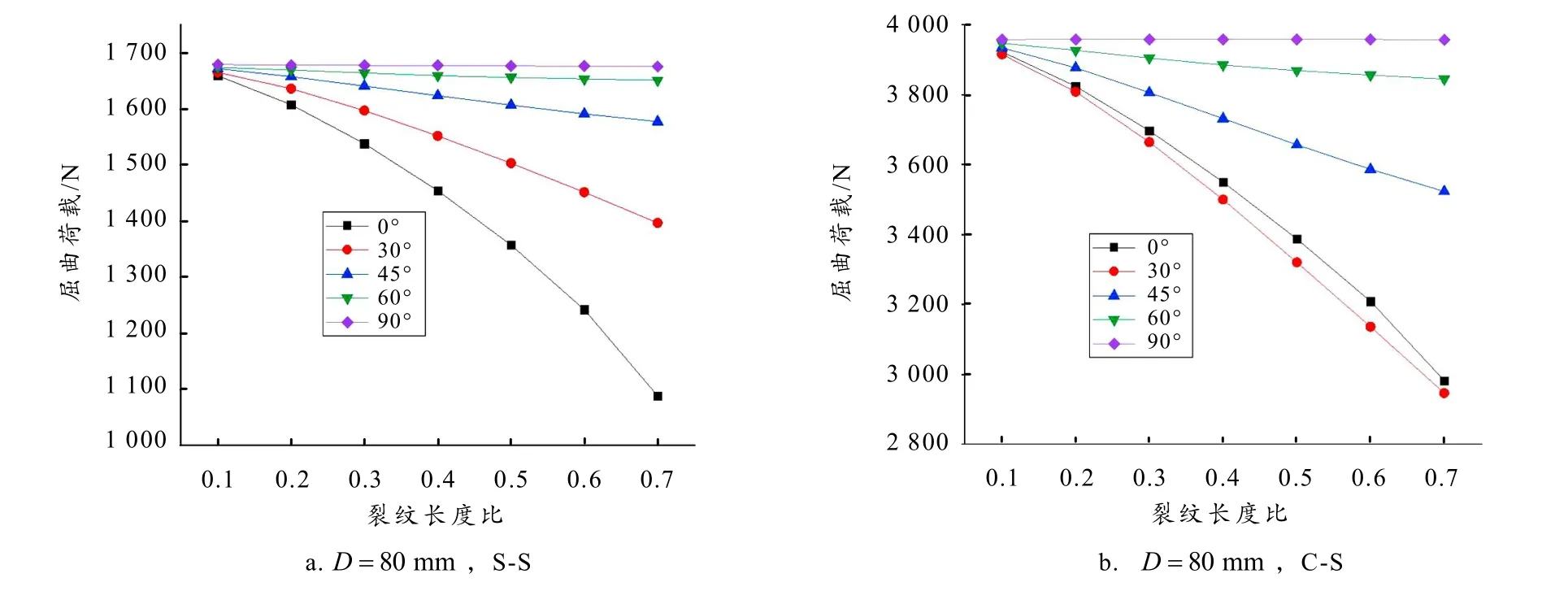
图8 裂纹长度比对屈曲荷载的影响

从图8 可以看出：1）随着裂纹长度比的增加，屈曲荷载明显下降，这种趋势在裂纹倾斜角度较小和孔径较大的时候更为明显.2）边界条件对屈曲荷载的影响是显著的，固支边界下薄板的承载力远高于简支边界下薄板的承载力.3）当裂纹长度比小于0.2 时，裂纹倾角对板件的屈曲荷载影响非常小，随着裂纹长度比的增加，裂纹倾角对屈曲荷载的影响才开始凸显，且出现两种极端情况，即当裂纹倾角为90°时，屈曲荷载基本不受裂纹长度的影响；而当裂纹倾角为0°时，裂纹长度对荷载的影响最大.

3.2 裂纹倾斜角对薄板屈曲荷载的影响

在有限元中取薄板长宽为200 mm，厚度为1.4 mm，孔的直径80 mm，裂纹长度比固定为0.5，研究裂纹倾角从0°逐渐增加到90°时，板件的屈曲荷载变化情况，其结果如图9 所示.

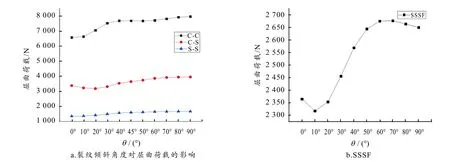
图9 裂纹倾斜角对屈曲荷载的影响

从图9-a 可以看出：1）在S-S 边界下，随着裂纹倾斜角的增加，钢板的屈曲荷载增幅逐渐增加，当倾斜角为60°左右时，屈曲荷载的增幅开始下降.2）在C-S 边界下，屈曲荷载随着裂纹倾斜角增大呈现出先减少再增加的趋势，屈曲荷载最小值出现在裂纹倾角为30°左右时，其原因可能是在边界条件对称的情况下，薄板刚度最薄弱的位置出现在中部，而当边界条件不对称时，薄板刚度最薄弱的位置会出现一定的偏移.3）在C-C 边界下，屈曲荷载随着裂纹倾斜角的增加趋势显著变快，在倾斜角为 40°至60°时趋于平稳，然后随着裂纹倾斜角的变大荷载持续增加，但是增幅明显比在10°至40°时小.

在图9-b 中，SSSF 边界下，屈曲荷载随着裂纹倾角的增加先下降，最小值出现在裂纹倾斜角度为10°时，然后上升，当裂纹倾角大于60°时趋于平稳；当裂纹倾斜角为30°至60°时，倾斜角对屈曲荷载的影响更为明显.而当裂纹倾斜角度大于60°后，随着角度增加荷载值逐渐收敛.其原因可能是较大的裂纹倾斜角度会使得裂纹位置发生改变，裂纹由中部逐渐向中上部移动，使得裂纹不再位于薄板的刚度薄弱区，同时较大的倾斜角度会使得薄板在受压方向的损伤减少，其抗弯刚度得到了一定的提升，所以此时裂纹角度变化对其临界荷载的影响逐渐减少.

3.3 板件开孔率（开孔面积/开孔前薄板面积）对屈曲荷载的影响

在有限元中取薄板长宽为200 mm，厚度为1.4 mm，研究不同边界条件下，薄板开孔率从0 到0.7 时，板件的屈曲临界荷载的变化情况如图10 所示.

从图10 中可以看出，随着开孔率的增加，板件的屈曲荷载逐渐下降，同时降幅也逐渐减小.在S-S边界条件下，曲线相对平缓，呈下凹的形式；C-S边界下，在开孔率为0 至0.1 时屈曲荷载下降幅度最大，同时下凹的趋势放缓；在C-C 边界下，当开孔率为0 至0.1 时，随着开孔率的增加屈曲荷载快速下降，但是在开孔率为0.1 至0.7 时，开孔率和屈曲荷载大致呈线性关系.

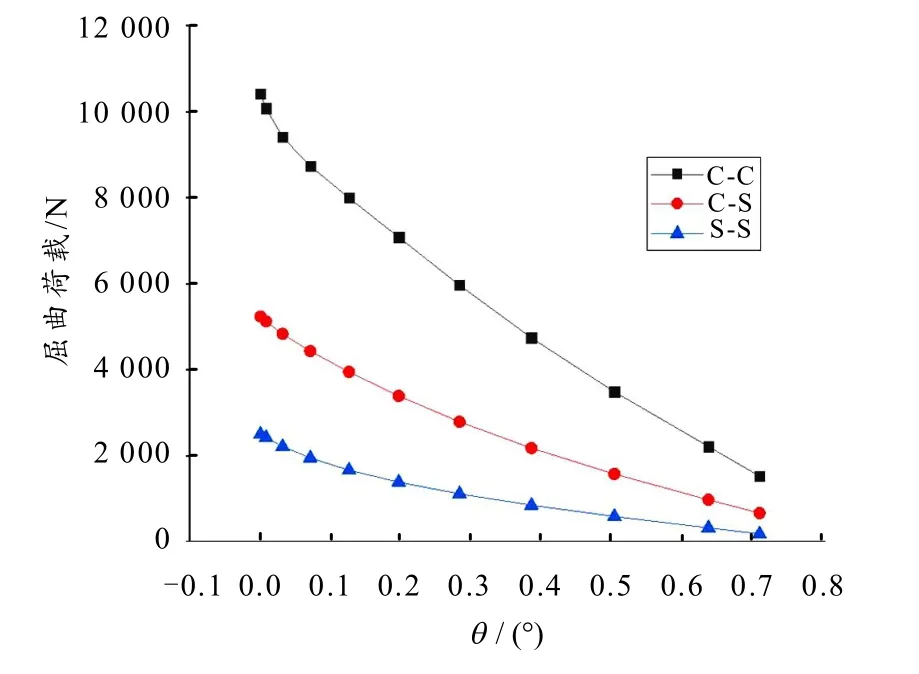
图10 薄板开孔率对屈曲荷载的影响

3.4 屈曲系数经验公式

基于上述有限元的分析结果，通过MATLAB 采用最小二乘法对各种因素下含孔边裂纹薄板的屈曲承载力的有限元结果进行二次拟合，得到含孔边裂纹板的屈曲系数k.

在S-S 边界条件下，含孔边裂纹板的屈曲系数拟合函数如下（R2= 0.935）：

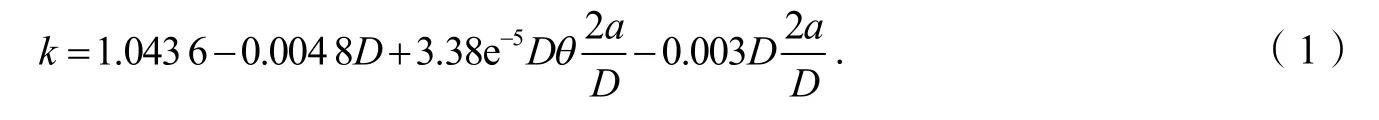
在C-S 边界条件下，含孔边裂纹板的屈曲系数拟合函数如下（R2= 0.978）：

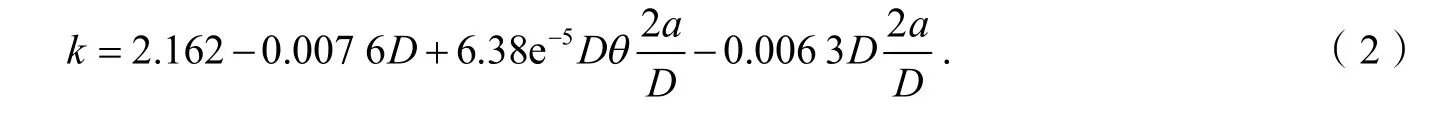
在C-C 边界条件下，含孔边裂纹板的屈曲系数拟合函数如下（R2= 0.927）：

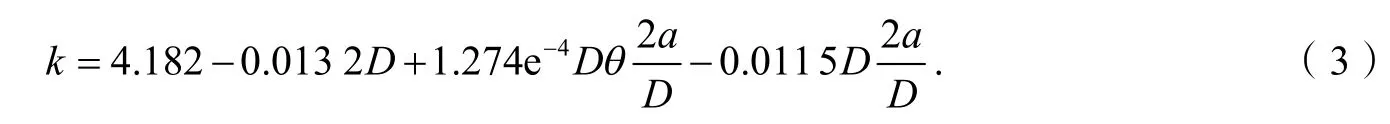
在SSSF 边界条件下，含孔边裂纹板的屈曲系数拟合函数如式如下（R2= 0.986）：

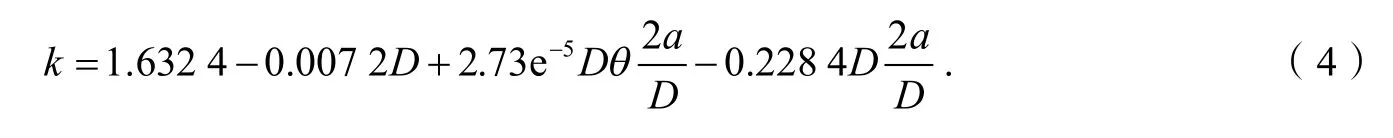
在SSSS 边界条件下，含孔边裂纹板的屈曲系数拟合函数如下（R2= 0.932）：

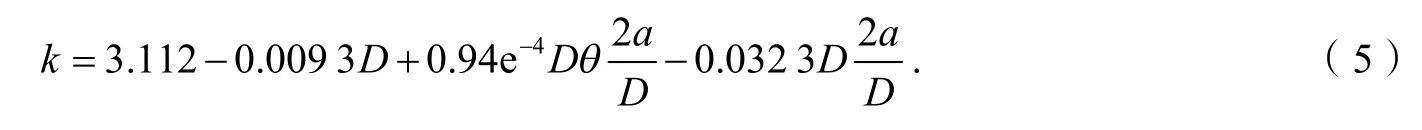
其中D为圆孔直径，θ为裂纹倾斜角，a为板裂纹长度.

选取θ=0°，a=0.1，D=0.8代入式（2），计算k= 2.162 - 0.007 6D- 0.006 3 ·，得：k= 1.492.

根据板壳理论，均匀轴向压缩荷载下矩形薄板的临界应力计算如下：

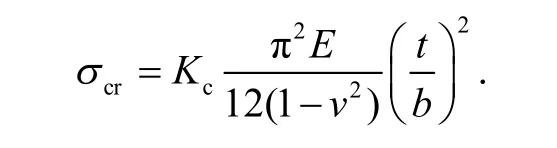
其中，Kc为临界屈曲系数；v为板材的泊松比；t为材料的厚度；E为弹性模量；b为薄板加载边的宽度.根据Q235 钢的力学性能，取v=0.3，E= 207 GPa，本文板的尺寸：t= 1.4 mm，b= 200 mm，由飞机设计手册查得Kc=1.6，则σcr= 14.65 MPa，计算有：Fcr= 4102 N.而当k= 1.492，其σ= 13.66，计算屈曲荷载：FN= 3826 N.根据表1 的实验结果，屈曲荷载为：3 924 N.三者比较，式（2）拟合出来的屈曲系数k的误差大约为2.6%，而理论屈曲系数Kc的误差大约为4.5%.所以本文的屈曲系数更加接近工程实际.

4 结论

本文对含孔边裂纹薄板进行了轴心受压试验，结果表明：板件开孔率、裂纹长度、裂纹倾斜角度和边界条件都会显著影响薄板的屈曲荷载；对于开孔率（孔径）较小或裂纹长度较小的薄板，裂纹倾斜角度的变化对其屈曲荷载影响较小.基于有限元分析软件 ABAQUS 对含孔边裂纹薄板进行了屈曲性能分析，细化了裂纹长度、倾角和分布方式对屈曲荷载和极限荷载的影响，并基于大量的有限元计算结果，采用最小二乘法对5 种边界条件下含孔边裂纹板的屈曲系数和极限荷载进行了拟合，得到了含孔边裂纹薄板屈曲系数和极限荷载的经验公式.本文结果主要针对含有单个圆孔的情况，对于含有多孔多裂纹的情况需要进一步探索.另外，本文仅对板件的轴心压缩展开了研究，对于偏心压缩还需要进一步探索.