“形”中挖“同” “数”中寻“构”
——记“同构思想”在解析几何中的应用
常梨君 金一鸣 (江苏省常州市田家炳高级中学 213001)
平面解析几何是高中数学的一大重点和难点,对数学运算有着较高的要求,学生普遍具有“畏算”心理.而新高考背景下对运算能力提出了高要求,运算是大量的,而且是实的,不仅要有精细迅速的运算技能,还需依据条件和目标不断确定和调整运算方法和路径,在运算中彰显能力.现实与目标的反差,促使我们重新审视解析几何运算,从新的视角切入,引入新思想,另辟蹊径,才会“另有一番天地”.
1 优化解题,联想“同构”
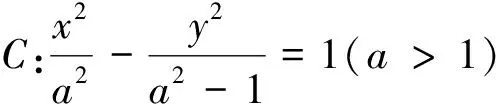
此题是21题的第一问,变量多,运算量大,学生在考试过程中不易做对.“由双曲线上的一点引两条斜率和为零的直线,则这两条直线与双曲线交点连线的斜率为定值”,这是本问的出题依据.学生常见的做法有如下两种:
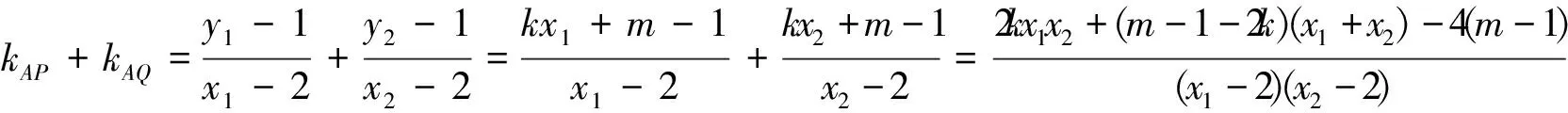
k=-1.
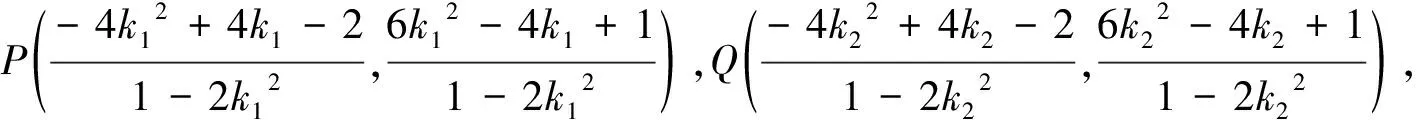
这两种解法分别体现了解析几何解题的两种思想:“设而不求”与“设而求之(点P,Q可求)”,学生常是有思路但算不到底,反映其对数学运算的设计和选择能力偏弱.能否优化呢?笔者注意到点P,Q的坐标结构相同,与“同构”似乎有着某种联系,不妨作一些尝试,对运算进行优化.
2 解析“同构”,迁移应用
“同构”是抽象代数中的专业术语,指的是一个保持结构的双射.数学中的同构式是指变量不同,但结构相同的两个表达式.所谓用同构思想解题,它来源于一个基础结论:若f(x)是定义在区间D上的增函数,则f(x)>f(y)⟺x>y(减函数结论类似).利用这个结论,构建同构式,抽象母函数,把函数值的关系转化为自变量的关系,脱去嵌套的外衣,实现化繁为简.因此,“同构”的本质是构造函数的思想,对学生的高阶思维有较高的要求.
解析几何问题中,常有一些点、线具有相同的特征(如,点A,B在曲线f(x,y)=0上),将这些“形”的共性坐标化,得到的代数式结构也相同,这为“同构法”的使用提供了可能.本文探究了“同构思想”在解析几何中的一些妙用,以期拓展思维,培养学生抽象和化归的思维能力,提升综合素养.
3 形相似切入,寻找同构点
3.1 同构点1——二次曲线上的两个点在同一条直线上

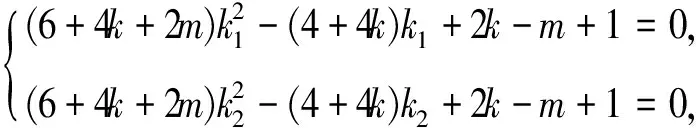
即k1,k2为方程(6+4k+2m)x2-(4+4k)x+2k-m+1=0的两个不等实根,
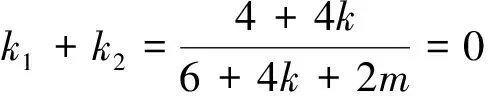
方向2 从点P,Q既是直线与双曲线的交点,又是两直线的交点入手,“算两次”:


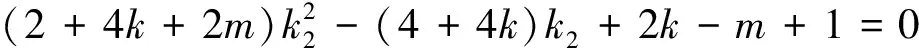
由①②可得k1,k2为方程(2+4k+2m)x2-(4+4k)x+2k-m+1=0的两个不等实根,
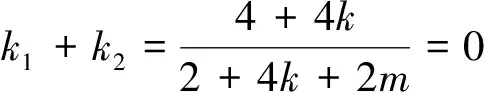
点评 点P,Q的坐标是关于k1,k2的二次式,且结构相同,代入直线PQ方程,得到了两个同构式,以k1,k2为主元整理,抽象出母方程(一元二次方程f(x)=0),由韦达定理得到结果.设而不求,避免了繁琐运算.“双曲线上的两个点在同一条直线上”这一“形似”,是构造同构式的关键.已知点P,Q坐标的前提下,“设直线、点代入”和“算两次”这一视角的转换也是难点.
3.2 同构点2——两个点在同一条二次曲线上


图1

能否用“同构”解答呢?我们作如下联想:①由“λ1+λ2”联想到什么?(韦达定理)→②如何构造λ的二次方程?→③题中有二次式吗?(椭圆方程)→④如何构造同构方程?(点A,B在椭圆上)→⑤如何求A,B坐标?(将上述方程①②中用λ表示x,y).
点评 直线MF上的点A,B(坐标结构相同)在二次曲线(椭圆)上,这是形似,以λ为主元构造出同构方程.此法摆脱了“直线与椭圆相交、联立、韦达定理”的固化思维,同构式以λ的新视角研究问题,不仅减少了大量运算,也彰显了思维的整体性和灵活性.
3.3 同构点3——两条直线与二次曲线有相同位置关系


图2
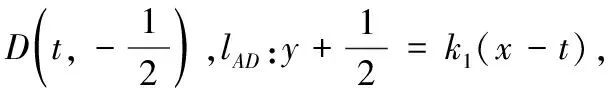
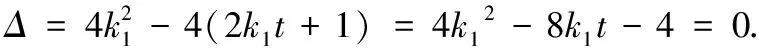

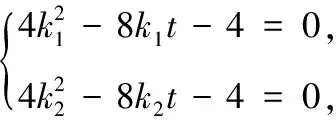
点评 这是抛物线中的阿基米德三角形,以极点(焦点)、极线(准线)为载体,“联立直线与圆锥曲线,消元,由相切得Δ=0”,是判定直线与圆锥曲线相切的通法.两条切线得到的两个判别式恰为关于k1,k2的同构式,采用整体消元,简化运算.
3.4 同构点4——两条直线过同一个点
再看问题3,开口向上的抛物线的切线问题,还可以用导数法解决.

点评 两条切线的方程结构相同,利用点D在两条切线上得到同构式,(**)式如何消元是关键.由目标直线方程的定义出发,消x2,直接构建x1,y1和x2,y2满足的方程(二元一次方程f(x,y)=0),出其不意,一步到位,且直线AB为抛物线的切点弦方程.
利用“同构”二元一次方程f(x,y)=0的方法,还可以推广到圆、椭圆、双曲线切点弦方程,结论如下:
(1)自圆C:(x-a)2+(y-b)2=r2(r>0)外一点P(x0,y0)作圆C的切线,切点为A,B,则切点弦AB的方程为:(x-a)(x0-a)+(y-b)(y0-b)=r2.
4 总结内化,提升素养
4.1 “同构法”解题的流程
根据上述三个例子,可以概括出使用“同构法”解题的流程为:
点(或线)满足的公共特征→构造“同构”→确定主元→抽象母方程→求解目标.
“同构法”解题是由几何特征的形似,抽象出代数式的同构,利用“整体消元”解决问题.学生在解决问题的过程中,明了同构是什么,同构能解决什么问题.同时,“确定主元”中主元的选择很重要,需要视问题的需要而定,可以是斜率、参数和坐标等.“同是形式、构是内涵”,思想方法的改变带来了低阶数学运算的大量简化,令人拍案叫绝,对学生高阶数学运算的提升很有裨益.同时,同构式也体现了数学的对称美、和谐美.
4.2 “同构点”的寻找
要想真正掌握并灵活运用“同构”,就必须选择好“同构点”,即同构式怎么构造?笔者分析研究整理出近年高考题中的部分“同构点”,如图3所示.

图3
形相似是使用同构的标志,在形数转化的过程中,“同构”实现了数形的完美结合.利用“式子结构”的整体性,实现了“设而不求”;“同构主元”的选择,突破了x,y的桎梏,新视角带来了不同的解题体验.
4.3 提升高水平的数学运算素养
《普通高中数学课程标准(2017年版)》要求学生具有理解运算对象、探究运算方向、选择运算方法、设计运算程序、求得运算结果等数学运算素养,并且将数学运算核心素养分为能够在熟悉的情境中了解运算对象,提出运算问题;能够在关联的情境中确定运算对象,提出运算问题;在综合情境中能够把问题转化为运算问题,确定运算对象和运算法则,明确运算方向这三个水平.
以问题1的“同构解法”为例,由双曲线上点P,Q的坐标结构的相似性,设直线方程,构造出同构式,是简化整个计算的关键步骤,对素养要求很高,是“水平三”;由同构式抽象出母方程,联系韦达定理,属于“水平二”;求点M,N的坐标则为“水平一”.由几何特征到同构式的转化为后续的计算指明了方向,转化的过程中不仅需要运算能力,更需要有反向推演的能力,高水平的数学运算一定有逻辑推理的参与.
将解析几何从“联立求解”转移到“识图析图”,从繁琐的数式运算转向分析推理型运算,让学生体会更多“设而不求”的计算精髓,才能真正提升学生的运算素养,培养学生不怕算的毅力,进而将解析几何运算进行到底.

