重差术:古人之智 几何之美
陈宇航 沙思远 (江苏省苏州市阳山实验初级中学校初三(2)班 215151)
指导教师 胡永强 (江苏省苏州市阳山实验初级中学校 215151)
近期,我们学习了相似三角形,在这一章的最后,学习了用相似三角形的相关知识解决中心投影下实际计算问题.我们从中发现数学知识可以解决许多实际问题,数学具有广泛的应用价值.下面选取一道典型例题作具体介绍.
例1如图1,AB为路灯,小明站在D处,影子是DF,他往前走到H处,影子是HI,若小明身高CD=GH=hm,影子DF=am,影子HI=bm,DH=dm,求路灯的高(用含a,b,h,d的代数式表示).
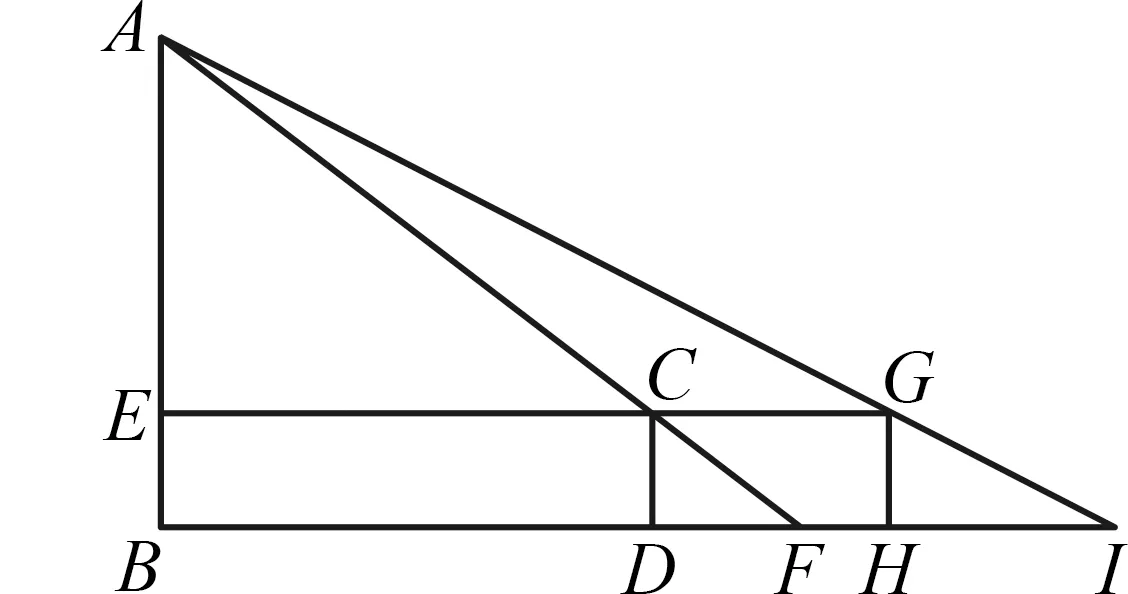
图1

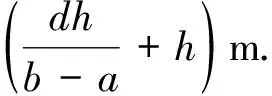
在学完课本中的方法后,老师告诉我们:我国古代数学中没有角的概念,也没有相似三角形的相关定理,但是我国古人对此类问题却有比较巧妙的解法.随后,老师让我们猜测:我国古代数学家在不用相似三角形知识的背景下,如何解决这种问题?同学们一时都不知道古人的方法.老师提醒道:“在勾股定理一章,我们见识了赵爽、刘徽等古代数学家用面积法解决许多问题,这种解决问题的思想方法叫‘出入相补原理’.大家可以从面积法的角度思考解决办法.”
在老师的引导和帮助下,我们一起见识与探究了我国古代数学家对此类问题的解法.具体如下:
首先,让我们一起了解一个重要的原理:如图2,矩形ABCD中,如果I为对角线BD上一点,GH和EF过点I,GH⊥AB,GH⊥CD,垂足分别为点G,H,EF⊥BC,EF⊥AD,垂足分别为点E,F,那么S1=S2.
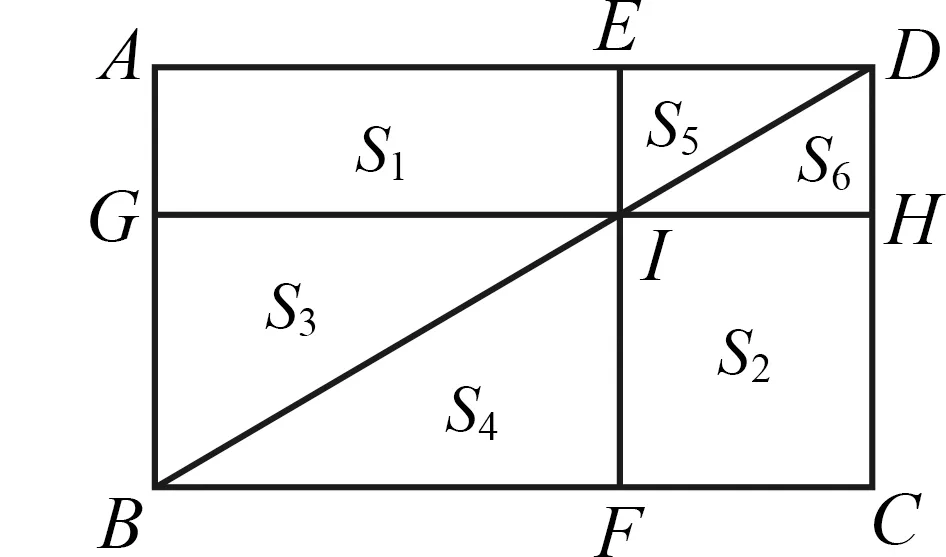
图2
证明因为对角线平分矩形面积,所以S1+S3+S5=S2+S4+S6.同理可得S3=S4,S5=S6.所以S1=S2.
我国古代数学家将这个原理称作“勾中容横,股中容直原理”.根据这个原理可以推算出计算AB高度的公式.
如图3,设CD=GH=BE=h,DF=a,HI=b,DH=d,我们用XBC表示矩形BDCE的面积.
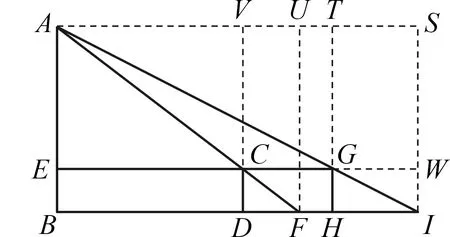
图3

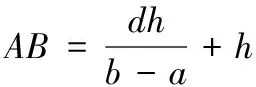
古人在一次又一次的演算与思考中获得真理,他们的智慧与钻研精神着实令人钦佩.不难发现,古今中外人们对测量问题都有研究,方法与原理也各不相同,各具特色,各有优势.我国古人更善于从一类问题中总结出一般性的结论与规律,并运用这些结论与规律解决同类问题.
指导老师点评中华优秀传统数学文化是中华民族共同的精神财富,其间蕴含着丰富的数学学习素材.在我国古代,与测量相关的技术称为“测望之术”,包括测高、测深、测远等.根据测望次数,又分为“一望”“二望”“三望”“四望”等.重差术公式主要用于解决“二望”问题.两位小作者研究了教材中的测量建筑物高度的方法和我国古代的“重差术”,发现古代数学家利用“勾中容横,股中容直原理”推算出解决这类问题的公式,只要测量出公式中的几个量,代入公式即可计算出物体的高度.同时,两位小作者还体会到我国古代数学家善于从一类问题中总结出一般性的规律与方法,并用其解决同类问题.这种机械化的算法思想是我国古代数学的一大特色.中华优秀传统数学文化博大精深,我们要认真研究,将其传承和发扬下去.

