非厄密电磁超表面研究进展

范辉颖 罗杰

(苏州大学物理科学与技术学院,苏州 215006)

电磁超表面是一类由单层或多层亚波长人工微结构组成的平面电磁材料,可以在亚波长尺度下实现对电磁波偏振、振幅和相位的有效调控.然而,将电磁波限制在深亚波长尺度的代价通常是大的损耗,如辐射损耗、欧姆损耗.有趣的是,非厄米物理提供了一种将损耗这一不利因素转变为超表面设计中一个新自由度的新方法,为扩展超表面功能提供了新方向.近些年,非厄米电磁超表面上的一些非常规物理效应引起了研究人员的广泛关注.本文从完美吸收、奇异点与表面波三个方面对非厄米电磁超表面研究进行了综述,并对该领域面临的挑战和发展前景进行了展望.

1 引言

根据经典电动力学理论可知,材料的电磁特性取决于介电常数、磁导率和电导率这三个宏观参数,它们共同决定了电磁波与材料的相互作用.由于天然物质的电磁参数范围非常有限,大大限制了它们对电磁波的操控能力.因此,为了获得具有近乎任意电磁参数的材料来实现对电磁波更大自由度的操控,电磁超材料[1−3]的概念于20 世纪末被提出,并兴起于21 世纪初.电磁超材料是一种由具有特定电磁响应的亚波长微结构单元所组成,且具有天然物质所不存在的电磁特性的人工微结构材料.

电磁超表面[4−30]可以看作是电磁超材料的二维平面形式,由单层或多层亚波长人工微结构单元按照特定功能需要排列构成.通过设计微结构单元的几何结构和组分,可以在亚波长尺度下实现对电磁波偏振、振幅和相位的有效调控[4−30].与三维超材料相比,超表面拥有厚度薄、损耗低、易于加工制备和集成等优点,其巨大的应用潜力受到全世界研究人员的广泛关注.近些年,研究人员相继提出了梯度超表面[31−35]、编码超表面[11,36,37]、可重构超表面[12,13]、非线性超表面[14−17]、惠更斯超表面[20,21,38]、布儒斯特超表面[39−41]等不同类型的电磁超表面,它们在超构透镜[30,42−46]、全息成像[47−49]、高效表面波耦合器[33,34,50]、偏振转换器[51,52]、涡旋光束发生器[31,53]、隐形斗篷[54−56]等应用方面显示了巨大的潜力和优势.然而,电磁超表面的损耗(如辐射损耗、欧姆损耗)是不可避免的,尤其是将电磁波限制在深亚波长尺度的代价通常是大的损耗[57,58].在电磁超表面的设计与应用中,损耗往往被看作是一个不利因素,其降低了超表面的工作效率[18],因此,通常会通过采用电介质材料等方法将损耗降到最低[27−29].

有趣的是,随着近些年非厄米物理的发展,研究人员意识到可以将损耗这一不利因素转变为电磁超表面设计中的一个新自由度,从而为扩展超表面功能和实现非常规物理效应提供了新方向.广义来讲,所有与环境交换能量的开放系统都是非厄米系统,其物理量可用非厄米算符描述.非厄米系统通常拥有复本征值和非正交本征态,同时会表现出特殊的简并点—两个或更多的本征值及相应的本征态同时简并,称为奇异点(exceptional point,EP)[59−61].

在光学/电磁材料中,折射率虚部反映电磁能量的增益和损耗,通过改变材料的结构和组分,可以轻易实现对增益/损耗的有效操控,因此,光学/电磁系统已成为非厄米物理研究的重要平台[62−74].这不仅对理解和拓展开放量子系统的基本问题具有重要的类比研究意义,也为人工结构材料领域的发展开辟一条新路径,带来了更丰富的物理效应和现象,包括微型激光[64,75−79]、相干完美吸收-激光器[80−83]、单向无反射[65,84−86]、奇异环与复狄拉克点[69,87,88]、无线能量传输[89−91]、高阶奇异点与超灵敏传感[70,92−98]等.

近些年,研究人员将非厄米物理与电磁超表面相结合,提出了非厄米电磁超表面[72−74,99−104](图1).早期非厄米电磁超表面的研究沿袭了非厄米电磁系统研究的基本思路,在平面内构建耦合结构单元,并通过等效非厄米哈密顿量来描述其电磁特性[105].随着近些年非厄米电磁理论的不断发展,“非厄米”已经逐步演变为“损耗或/和增益”的代名词[106,107].在很多情况下,非厄米电磁系统泛指存在损耗或/和增益的电磁系统.鉴于此,同时为了区别于传统电磁超表面,可以对非厄米电磁超表面作出广泛的一般定义,即包含损耗或/和增益,且拥有由损耗或/和增益诱导的显著电磁特性的电磁超表面.

图1 非厄米电磁超表面示意图Fig.1.Illustration of non-Hermitian electromagnetic metasurfaces.

非厄米电磁超表面为非厄米物理的研究提供一类全新的二维平台,而传统电磁超表面中损耗这一不利因素则借助非厄米理论转变为设计中的一个新自由度,由此产生了传统电磁超表面中不存在的非常规物理效应,包括完美吸收[99−104]、奇异点下的奇异物理特性(如单向无反射、偏振控制、衍射控制、超灵敏传感等)[72−74]、奇异表面波[108−110]等.非厄米物理为有效利用电磁超表面中增益和损耗,并扩展其功能提供了新的方法,把超表面的设计进一步扩展到复介电常数和磁导率的整个空间,为新型电磁器件的设计提供了新思路.

本文全面地综述了非厄米电磁超表面的理论与应用.首先介绍了谐振型与非谐振型非厄米电磁超表面在电磁波完美吸收上的应用.然后,介绍了耦合模型和散射模型的非厄米电磁超表面中奇异点的基本理论,以及由此产生的单向无反射、偏振控制、超灵敏传感、相位操控等重要应用.此外,还讨论了非厄米电磁超表面上的奇异表面波,包括自准直表面波和线波.最后,对该领域面临的挑战和发展前景进行了总结与展望.

2 非厄米电磁超表面的完美吸收

有效利用损耗最重要的例子是电磁超表面完美吸收体[99−103].关于电磁波吸收的研究一直都是电磁领域的研究热点,其无论在工程应用还是在国防军事中都是至关重要的.在众多电磁波吸收中,电磁超表面吸收体因具有厚度薄、体积小、结构简单、吸收率高等诸多优点,可广泛应用于电磁隐身、电磁屏蔽、热成像、热发射器、传感器等领域.本节主要介绍非厄米电磁超表面在电磁波完美吸收上的应用,根据原理的不同,分为谐振型与非谐振型两种类型进行讨论,相比于前者,后者具有超大吸收带宽等优势.

2.1 谐振型完美吸波超表面

通常情况下,吸收材料的阻抗无法与空气阻抗直接匹配,因而在吸收电磁波的同时也在反射电磁波.由此可见,要获得完美吸波超表面的关键是实现超表面与空气的阻抗匹配.阻抗匹配可以使得入射波无反射地进入到超表面中,并通过超表面中的欧姆损耗来耗散掉入射电磁波的能量.在宏观上,超表面表现为复数的等效电磁参数(相对介电常数εeff,相对磁导率µeff),且满足下面的阻抗匹配关系:

其中Zeff和Z0分别为超表面的等效波阻抗和自由空间中波阻抗;ε0和µ0分别为真空介电常数和磁导率.根据(1)式,阻抗匹配要求εeff=µeff.

基于阻抗匹配这一思路,Landy 等[111]在2008年首次提出了完美吸波超表面.他们设计了三层结构来实现对εeff和µeff的独立调控(图2(a)左图),顶层为金属开口谐振环结构,提供了电谐振响应,而磁谐振响应则是中间介质层中的磁场通过激发顶层开口谐振环的中心金属条与底层金属线中的反平行电流获得的.通过调控结构的几何参数,在11.65 GHz 处实现了εeff=µeff,并获得了高达99%的吸收率(图2(a)右图).值得一提的是,该完美吸波超表面的厚度不足波长的 1/30,这项开创性工作很快激起了一系列后续研究,工作频率领域覆盖了从微波到可见光等各个频段[112−135].

2010 年,Hao 等[112]和Liu 等[113]各自独立地设计出了近红外波段的吸波超表面,基本思想都是通过阻抗匹配最小化反射率,同时尽可能地通过超材料损耗消除透射率.他们都使用了上中下分别为周期性金属结构、介质层、金属衬底的三层结构模式,区别在于上层结构的不同,Hao 等采用的是矩形阵列结构(图2(b)),而Liu 等采用的是圆盘阵列结构(图2(c)).类似于Landy 等[111]提出的微波吸波超表面,顶层金属结构提供了电谐振响应,而顶层金属结构与底层金属衬底中的反平行电流提供了磁谐振响应.

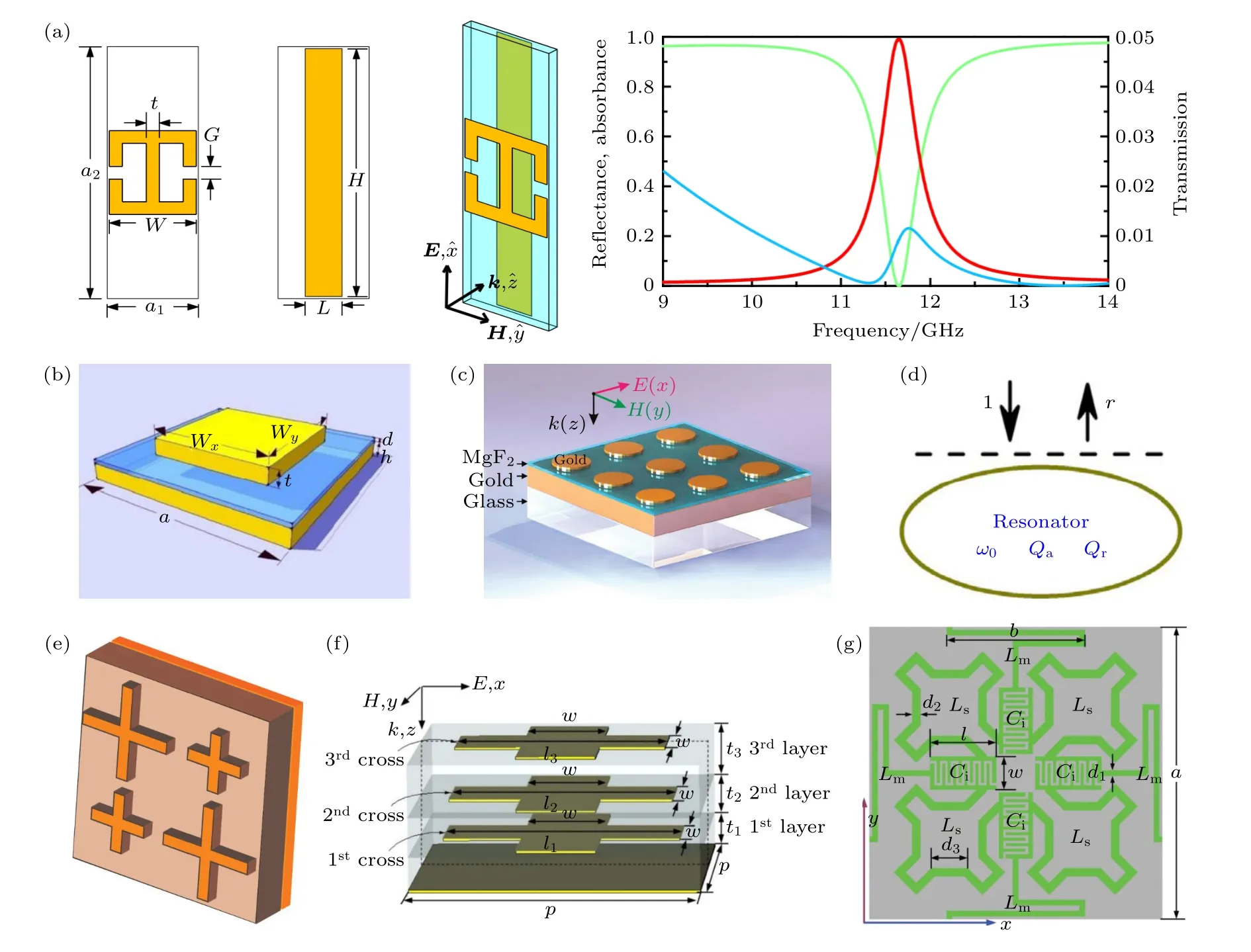
图2 谐振型完美吸波超表面 (a) 左: 超表面单元结构示意图;右: 吸波性能的仿真结果[111];(b) 光学吸波超表面单元示意图,顶部为金属矩形阵列[112];(c) 光学吸波超表面单元示意图,顶部为金属圆盘阵列[113];(d) 基于耦合模理论的等效单通道谐振腔模型[114];(e) 复合超表面结构单元,不同尺寸的谐振单元在横向上排布[115];(f) 复合超表面结构单元,不同尺寸的谐振单元在纵向上排布[116];(g) 拥有三个谐振频点的分形结构单元[119]Fig.2.Resonant absorbing metasurfaces.(a) Left: Illustration of the metasurface unit cell;Right: Simulated absorption spectrum[111].(b) An optical absorbing metasurface unit cell with an array of metallic disks on the top[112].(c) An optical absorbing metasurface unit cell with an array of rectangular metallic particles on the top[113].(d) The equivalent single-port resonator model based on coupled mode theory[114].(e) Composite metasurface unit cell consisting of horizontally arranged resonators of different sizes[115].(f) Composite metasurface unit cell consisting of vertically arranged resonators of different sizes[116].(g) Fractal unit cell exhibiting three resonant frequencies[119].

根据耦合模理论,这样三层结构的超表面还可以等效看作是一个与外部光波耦合的单通道谐振腔(图2(d))[114],其反射系数为

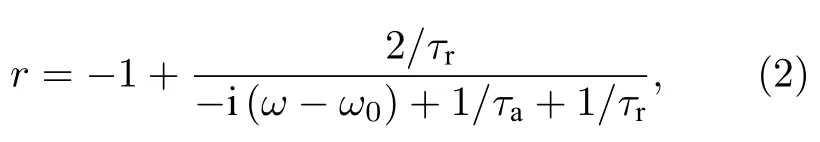
其中ω为入射光角频率;ω0为超表面的共振角频率;τa和τr分别是由欧姆损耗和辐射损耗引起的共振态寿命.无量纲参数Qa=ω0τa/2和Qr=ω0τr/2 分别描述系统的吸收和辐射质量因子,它们依赖于超表面单元的结构形状与几何参数.由(2)式可得,当ω=ω0时,反射系数完全由Qa和Qr决定.通过调节顶层金属结构的参数以及中间介质层的厚度,可以使得Qa=Qr,此时,r=0 .由于金属衬底消除了透射通道,零反射系数意味着100%吸收.这一理论模型对完美吸波超表面的设计具有重要的指导意义.

然而,谐振的本性决定了超表面有限的吸收带宽,这大大地限制了吸波超表面的应用范围.为了扩展吸收带宽,研究人员提出了利用多个或者多层工作在相邻频点的复合谐振单元[115−117],以及拥有不同谐振频点的单个结构单元[118−120]的方法.例如,Liu 等[115]在每个结构单元中横向排布了不同尺寸的谐振器来产生多个共振吸收频率(图2(e)).Ye 等[116]则在纵向上放置了三层不同尺寸的谐振结构,并使这三个结构对应的三个吸收频率足够接近,从而形成宽带吸收(图2(f)).Xu 等[119]设计了分形结构单元(图2(g)),利用分形结构的自相似性巧妙构建了多个局域谐振回路,实现了S,C 和X 波段同时工作的三频吸波超表面,三个工作频段内的吸收率均大于90%,且对极化和入射角不敏感.除此以外,研究人员还尝试采用了色散调制[121]、梯度结构[122,123]、无序结构[124,125]等方法来进一步扩展超表面的吸收带宽.总的来讲,这些结构都是通过不同频点的电磁共振结构的组合来实现宽频的吸收,虽然可以获得较好的吸收效果,但是尺寸大小的控制,以及结构单元的复杂制作工艺都为宽频吸波超表面的设计与实际应用带来了挑战.

2.2 非谐振型超宽频完美吸波超表面

尽管通过以上方法可以在一定程度上扩展电磁超表面的吸收带宽,但始终还是受限于其谐振本性.为了彻底克服谐振导致的有限吸收带宽这一问题,2021 年Luo 等[39]首次提出了一种非谐振的吸波超表面,即布儒斯特超表面,其由一介质平板及置于其中的倾斜金属薄膜阵列构成(图3(a)左图).在理论上,布儒斯特超表面可以在从准静场到光频的超宽频段内实现无反射的完美吸收.这一超宽频特性源于其背后的物理机制,即反常布儒斯特效应[39],这是将经典布儒斯特效应、光学互易原理以及各向异性介质中丰富的参数自由度(各向异性介电常数、光轴倾斜角)结合起来获得的新物理效应.

基本原理为横磁偏振的电磁波从左侧以介质的布儒斯特角入射,如果介质中倾斜金属薄膜平行于介质中的折射波(介质中电场垂直于金属薄膜),金属薄膜将不会影响电磁波的传播(图3(a)中图),此时,将出现因布儒斯特效应引起的超宽频无反射现象.进一步地,由光学互易原理可知,当入射方向翻转到右侧,且保持入射角大小不变时,其反射特性将保持不变[136].这意味着,右侧入射的电磁波也将产生超宽频无反射.有趣的是,此时介质中的电场方向不再垂直于金属薄膜,平行于金属薄膜的电场分量将会引起表面电流,从而造成入射电磁波的损耗,最终实现超宽频的无反射吸收.这一吸收材料上的超宽频无反射现象被称为反常布儒斯特效应[39].不同于传统吸波超表面利用电磁谐振获得阻抗匹配的方法,布儒斯特超表面则借助非谐振的反常布儒斯特效应获得了超宽频阻抗匹配特性,其结构更加简单,却拥有更大的吸波带宽,原则上可以从准静场一直到光频段.基于这一机理,Fan 等[40]设计了从光频到近红外频段的布儒斯特超表面,在反常布儒斯特角 −55.6◦附近,获得了400—1400 nm波长范围内大于90%的吸收率(图3(a)右图).Ma等[41]结合相变材料实现了从完美吸收到完美透明的超宽频动态调控.近期,Fan 等[137]进一步提出了基于反常广义布儒斯特效应的一类新型布儒斯特超表面,能够在掠射下实现对电磁波的超宽频无反射吸收.但是,需要指出的是,布儒斯特超表面在获得超大吸波带宽的同时产生了对入射角与偏振的依赖性.通常情况下,布儒斯特超表面只能对特定入射角和偏振的电磁波实现超宽频完美吸收.

图3 非谐振型超宽频完美吸波超表面 (a) 左: 布儒斯特超表面示意图;中: 原理示意图;右: 吸波性能的仿真结果[40];(b) 超宽频相干完美吸收的原理示意图[140];(c) 超宽频相干完美吸收的测量装置示意图,以及实验测得的反射率和吸收率与频率的关系[139]Fig.3.Non-resonant ultra-broadband absorbing metasurfaces.(a) Left: Illustration of the Brewster metasurface;Middle: The underlying physics;Right: Simulated absorption spectrum[40].(b) Illustration of ultra-broadband coherent perfect absorption[140].(c) Illustration of the experimental setup,and measured reflectance and absorptance as the function of frequency[139].

另一方面,通过改变入射电磁波的照射方式也可获得非谐振的超宽频完美吸收.2010 年,Chong等[138]提出了相干完美吸收的新概念,即通过两个及以上的相干光束同时照射到吸收体上来实现完美吸收,该想法一经提出就引起了研究员的广泛兴趣[101,130,139−145].2014 年,Luo 等[130]在理论上发现,当电磁超表面的表面电阻Rs满足:

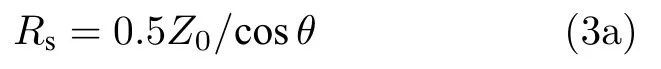
或

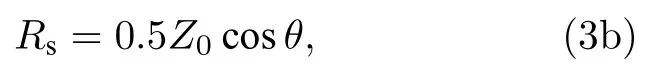
就可以实现对横电波或横磁波的超宽频完美吸收,其中θ为入射角.这是因为电磁波在该超表面上的反射系数r和透射系数t满足如下形式:

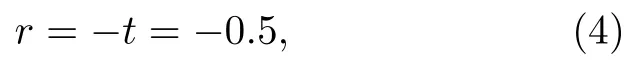
且与入射频率无关.此时,左侧入射电磁波的反射波与右侧入射波在左侧的透射波干涉相消,同样地,右侧入射电磁波的反射波也会与左侧入射波在右侧的透射波干涉相消(图3(b)).最终,左右两侧将都没有净出射波,所有入射波均被中间的超表面完全吸收.在物理图像上,相对照射的电磁波会干涉形成驻波,此时将拥有合适表面电阻值的电磁超表面置于驻波波腹处,即可实现对所有入射波的完美吸收[139].

2015 年,Li 等[140]通过微波实验证实了非谐振超表面的超宽频的相干完美吸收.实验装置为左右各一个矩形喇叭天线(图3(c)左图),它们辐射的电磁波相向垂直照射到置于中间的由导电薄膜构成的电磁超表面上,其表面电阻为Rs=180 Ω≈0.5Z0,厚度约为 3μm (约为真空中波长的万分之一),实验结果显示在 6—18 GHz 频段内获得了近乎为100%的吸收率(图3(c)右图),频率范围受限于实验测量装置.原则上,完美吸收频段可以覆盖从准静场到微波甚至太赫兹的超宽频率范围.近期,这一超宽频吸收原理已经被应用于表面等离激元的相干完美吸收[141].值得一提的是,通过改变不同入射波之间的相位差,可以让吸收率在0 到100%之间改变,这为吸收率的调控提供了一个非常有效的手段.然而,这种特殊的多波束配置大大限制了它的实际应用场景.

3 非厄米电磁超表面中的奇异点

奇异点是非厄米系统中的特殊简并点,系统中两个或更多的本征值及相应的本征态同时简并[62−74].在非厄米电磁超表面中,研究人员发现在奇异点附近的相变会导致许多有趣的现象.本节主要介绍耦合模型和散射模型的非厄米电磁超表面中奇异点的基本理论,以及由此产生的单向无反射、偏振控制、超灵敏传感、相位操控等重要应用.

3.1 耦合模型及在偏振操控上的应用

根据耦合模理论[146],由两个耦合谐振单元组成的二能级系统(图4(a)左图)的哈密顿量表示为[147−152]

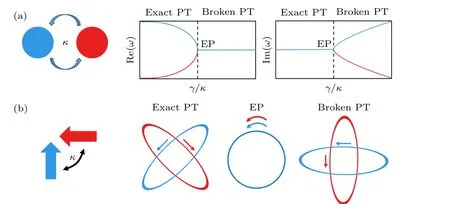
图4 非厄米电磁超表面的耦合理论模型 (a) 左: 两个耦合谐振单元组成的二能级系统;右: 本征值的演化;(b) 左: 两个具有正交激励方向的偶极子组成的二能级系统;右:本征值的演化Fig.4.Coupling model of non-Hermitian electromagnetic metasurfaces.(a) Left: A generic two-level system consisting of two coupled resonators;Right: The evolution of its eigenvalues.(b) Left: A generic two-level system consisting of two perpendicular dipoles;Right: The evolution of its eigenvalues.

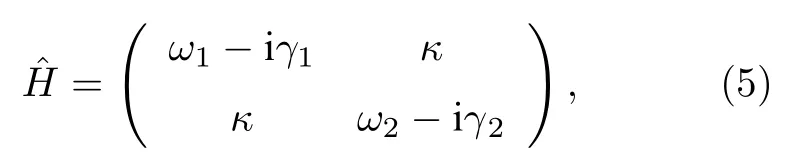
其中ω1,2是耦合谐振单元的共振频率,γ1,2是增益或损耗系数,κ是耦合谐振单元之间的耦合强度.该哈密顿量的两个本征值为

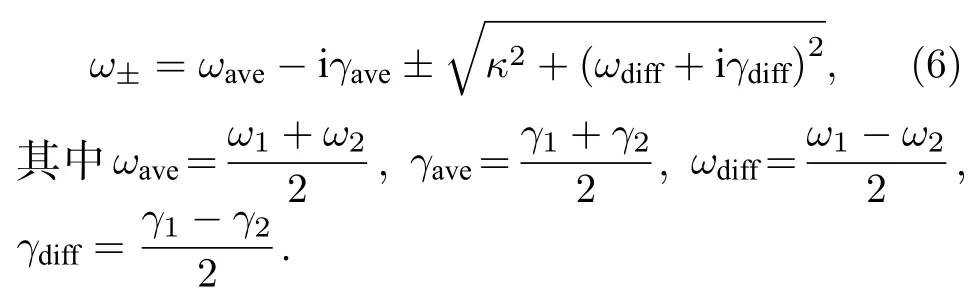
根据(6)式可知,当κ2+(ωdiff+iγdiff)2=0 时,两本征值相同,即ω+=ω−=ωave−iγave,此时,它们对应的本征态也相同,即 (ωdiff−iγdiff)/2κ,1)T.这表明,系统中的两个本征值及相应的本征态同时简并,这样的特殊简并点即为奇异点.

特殊地,当ω1=ω2=ω0且γ1=−γ2=γ时,系统具有宇称-时间反演(parity-time,PT)对称性[62−74],此时哈密顿量满足,这里的P和T分别为宇称变换和时间反演变换.PT 对称这一概念最早是由Bender 和Boettcher[153]在研究非厄米量子系统时提出的,他们发现如果势能为复数,且满足V(r)=V ∗(−r),非厄米系统也可能拥有实数的能谱.在电磁系统中,复势函数对应于复电磁参数,例如,复折射率满足n(r)=n∗(−r),折射率的实部偶对称,在耦合系统中表现为相同的共振频率,即ω1=ω2=ω0;折射率的虚部奇对称,表明系统拥有平衡的电磁增益和损耗,即γ1=−γ2=γ.这样的PT 对称系统的哈密顿量可以写作:

其本征值为

根据(8)式可知,奇异点的条件为κ=±γ,此时,两个本征值及相应的本征态同时简并(图4(a)右图).当 |γ|<|κ|时,本征值为两个不同的实数,系统处于PT 对称相,系统中电场在增益和损耗谐振单元中呈对称分布,总电磁能量守恒;而当|γ|>|κ|时,本征值为两个不同的复数,系统处于PT 破缺相,电场呈不对称分布,电场主要集中在增益或损耗谐振单元中,系统中的电磁能量呈指数增长或衰减.

在实际应用中,要精准控制材料增益系数,并使其与损耗系数平衡是非常困难的.有趣的是,即使在无源的纯损耗系统中,通过将哈密顿量作如下分解:

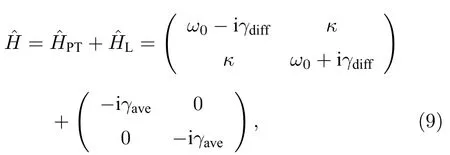
也可以观察到PT 对称相变,以及奇异点附近的奇异物理效应.其中为PT 对称哈密顿量,为不影响相变的系统衰减量.通过这种方式创建了“虚拟增益”来与损耗实现平衡[86,142,154,155].此时,可以借助来研究系统的PT 对称相、破缺相和奇异点,区别于严格PT 对称系统的是,PT 对称相和奇异点下的能量本征值因全局损耗的存在而不再为实数.

图4(b)给出了另一类重要的耦合模型,它是由两个具有正交激励方向的偶极子组成的二能级系统.该系统的等效PT 对称哈密顿量可以写为[105]

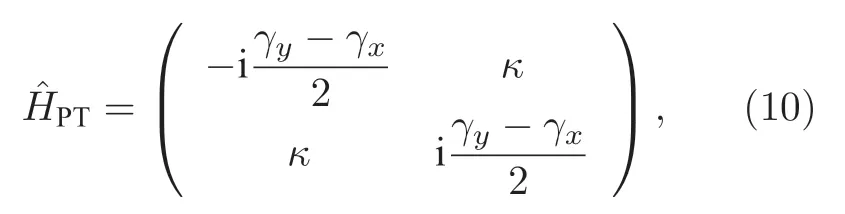
其中γx和γy分别为两偶极子的损耗或增益吸收;κ为两偶极子间的耦合吸收,其依赖于两偶极子之间的距离.该等效PT 对称哈密顿量的本征值为

根据(11)式可知,奇异点出现在2κ=|γx −γy|的条件下.当 2κ>|γx −γy| 时,系统处于等效的PT对称相,本征极化态为对应于沿±45◦方向旋转且相互垂直的两个椭圆(图4(b)右图),其中θ=sin−1[(γx −γy)/2κ] .而 当 2κ<|γx −γy| 时,系统处于破缺相,本征极化态为对应于沿 0◦和 90◦方向旋转且相互垂直的两个椭圆,其中θ=cosh−1[(γx −γy)/2κ].特殊地,在奇异点下(即2κ=|γx −γy|),本征值简并,同时本征极化态简并为一圆偏振态.

基于这类耦合模型的非厄米电磁超表面为电磁波偏振和手性操控提供了新的自由度,即损耗和增益,也由此产生了一些有趣的现象,如方向依赖的极化转换和涡旋光束产生[105,156−165].例如,2014 年,Lawrence 等[105]设计了各向异性吸收的非厄米超表面,每个结构单元由两个开口方向垂直的开口环谐振器组成(图5(a)左图),相当于共振频率相同,但激励方向正交的偶极子,它们之间的耦合强度可以通过改变间距来进行有效调控.损耗系数则是通过选用不同金属材料来改变的,左侧开口的环谐振器的材料为银,而上侧开口的环谐振器的材料为铅,由于银的欧姆损耗远小于铅,从而构建了一个各向异性吸收的非厄米超表面.研究发现,通过改变耦合强度,可以直接观察到系统本征偏振态的相变.有趣的是,尽管该非厄米超表面不具有旋转对称性,但在奇异点处,两个本征极化态合并为圆极化态,这一特性使得非厄米超表面具有不对称的偏振转换功能(图5(a)右图),这为偏振调制提供了一种新方法.

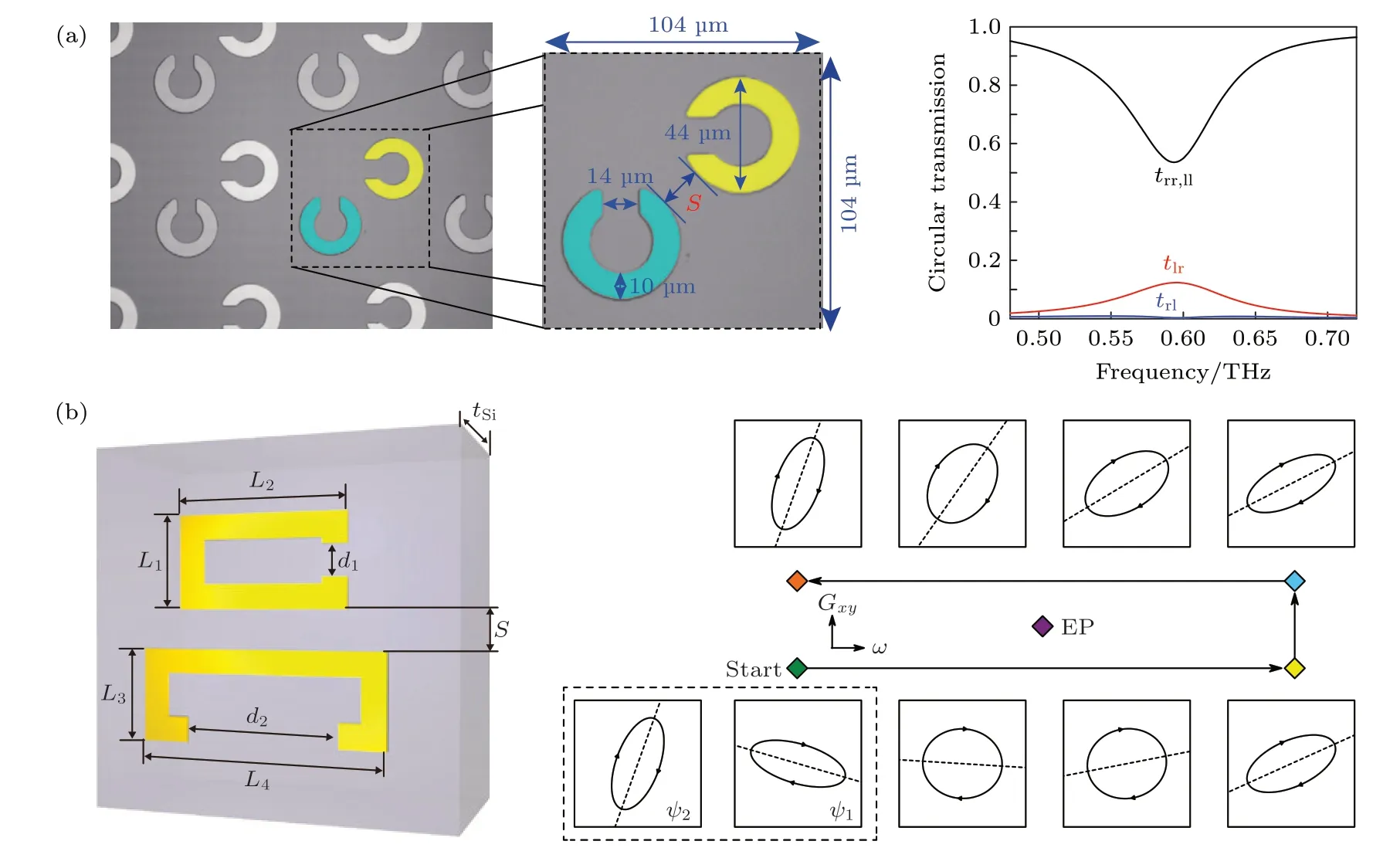
图5 非厄米电磁超表面 (a) 左: 由开口方向垂直的开口环谐振器阵列构成的非厄米超表面;右: 圆偏振入射波在超表面中的透射率[105];(b) 左: 非厄米超表面单个单元的几何结构;右: 本征态在参数空间中围绕奇异点的演化[156]Fig.5.Non-Hermitian electromagnetic metasurfaces.(a) Left: A non-Hermitian metasurfaces consisting of an array of orthogonally oriented split ring resonators;Right: The transmission of circularly polarized waves on this metasurface[105].(b) Left: Schematic of the metasurface unit cell;Right: The evolution of the eigenstates in parameter space as the EP is encircled[156].

Park 等[156]还设计了一种具有类似结构的非厄米电磁超表面(图5(b)),并在入射频率和耦合强度构成的参数空间中探索奇异点的拓扑结构.在数学上,奇异点对应于参数空间构成黎曼面的分叉奇点[166],这种独特的拓扑结构,使得围绕奇异点的一个完整环路下的本征态不会回到自身,而是相互交换,并积累 π 的几何相位.Park 等[156]在实验中观察到了非厄米电磁超表面上的本征偏振态交换现象,以及几何相位的积累,验证了奇异点的拓扑结构.

3.2 散射模型及单向无反射效应

非厄米电磁超表面也可以通过散射模型来研究超表面与外部电磁波的相互作用.散射模型通常用散射矩阵S来将入射波和出射波直接关联起来,它可以由传输矩阵[167]、阻抗或导纳矩阵[168]得到,也可以与耦合模式方程[86,169]结合.对于一个双端口的散射模型,其散射矩阵可表示为[86]

其中rL(R)和tL(R)分别为电磁波从左(右)侧入射时的反射和透射系数.在互易系统中,有tR=tL=t[136,170].该散射矩阵的本征值为

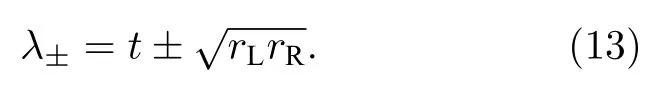
在没有吸收或增益的情况下,散射矩阵是幺正的,即S+S=1,其本征值的模始终为1,即散射矩阵的本征值位于复空间中的单位圆上.此时,系统能量满足广义的能量守恒,形式如下[171]:

其中RL(R)≡|rL(R)|2和T ≡|t|2分别为电磁波从左(右)侧入射时的能量反射率和透射率.

而当系统存在吸收或增益时,散射矩阵的本征值的模通常不再为1,本征值将向复空间中单位圆内部或外部偏离(图6).有趣的是,研究人员发现在PT 对称系统中,当T <1 时,散射矩阵本征值的模仍为1,且系统满足广义的能量守恒(即(14)式),此时系统处于PT 对称相;而当T >1 时,散射矩阵的本征值的模不等于1,两个本征值将会分叉,一支朝向单位圆内部,一支朝向单位圆外部,此时系统处于破缺相.散射矩阵的本征值在单位圆上的分叉点即为奇异点,此时,T=1且RLRR=0 .由于通常只有RL或RR等于零,因此这一奇异点效应也称为单向无反射效应或单向透明[84].

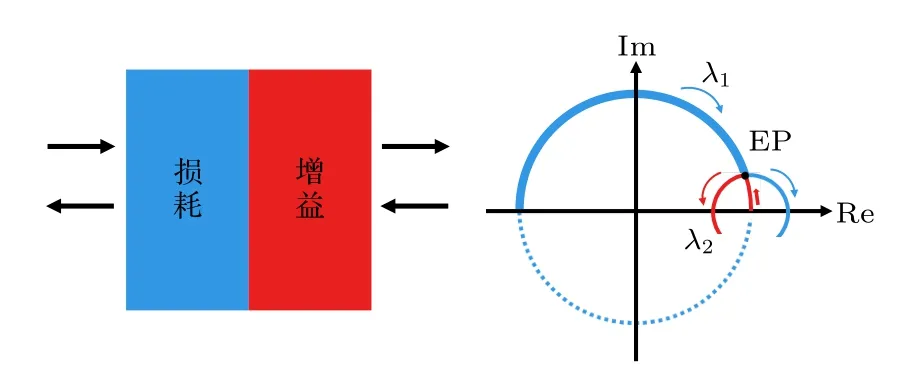
图6 (a) 非厄米电磁超表面的散射理论模型;(b): 本征值的演化Fig.6.(a) Scattering model of non-Hermitian electromagnetic metasurfaces;(b) the evolution of eigenvalues.

这一奇异点诱导的单向无反射效应也在非厄米电磁超表面系统中被观察到,并进一步激发了更多有趣的物理效应与应用[168,172−181].例如,2014 年,Fleury 等[172]提出了由一对平衡损耗和增益的超表面相对放置构成的PT 对称超表面系统,超表面的损耗或增益通过表面导纳来描述(图7(a)左图).研究发现,通过改变超表面的表面导纳,可以获得PT 相变奇异点,在该奇异点下,当电磁波从损耗超表面一侧入射时,将出现单向无反射负折射现象(图7(a)右图).基于这一奇异点,研究人员还进一步提出了单向无反射成像[173](图7(b))、单向隐身[174]、隐态传输[175]等有趣的物理现象和重要的应用.

值得一提的是,2018 年,Luo 等[176]指出这一PT 对称超表面系统存在两类物理机理完全不同的奇异点,而先前的研究都是基于第一类奇异点,在该奇异点下,损耗超表面以完美吸收体的形式工作,而增益超表面以激光器的形式工作.而Luo 等[176]研究发现,该系统还存在另一类奇异点,在这类奇异点下,损耗和增益超表面都以减反膜的形式工作.有趣的是,当超表面之间介质的介电常数趋于零时,即中间介质为零折射率介质[182−185],两类奇异点趋于合并(图7(c)左图).更加有趣的是,合并的奇异点诱导了一种新的物理效应,即对杂质免疫的完美传输.研究发现,在合并的奇异点下,当电磁波从损耗超表面一侧入射时,无论中间的零折射率介质中包含何种杂质,电磁波的透射率始终为100% (图7(c)右图).这完全消除了Liberal 等[186]在零折射率介质中发现的“光子掺杂”效应,也打破了杂质免疫现象只能发生在拓扑绝缘体的表面或边界处这一限制,对体波实现了对杂质免疫的完美传输.

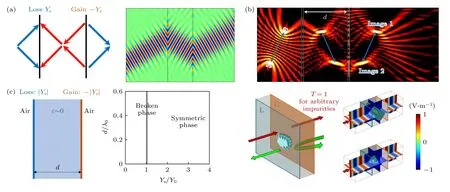
图7 PT 对称电磁超表面中的奇异点及单向无反射特性 (a) 左: 由一对平衡损耗与增益的超表面构成的PT 对称超表面系统示意图;右: 奇异点诱导的单向无反射负折射现象[172];(b) 奇异点诱导的单向无反射成像[173];(c) 左: 当超表面之间为零折射率介质时,系统中的两类相变奇异点趋于合并;右: 合并奇异点诱导的对杂质免疫的完美传输效应[176]Fig.7.EPs and unidirectional reflectionless properties of PT-symmetric electromagnetic metasurfaces.(a) Left: Illustration of a PTsymmetric metasurface system composed of a pair of metasurfaces with balanced loss and gain;Right: EP-induced unidirectional reflectionless negative refraction[172].(b) EP-induced unidirectional reflectionless imaging[173].(c) Left: Two classes of EPs tend to coalesce into one when the material between the two metasurface is an zero-index medium;Right: Coalesced EP-induced impurity-immune perfect wave transmission[176].

在实际设计中,吸收超表面的实现相对容易,在可见光和红外波段可以采用铬、钛、钨等大损耗金属[40],在太赫兹和微波频段可以采用氧化铟锡[39]、石墨烯[187]等导电材料;另一方面,增益超表面的设计,及其增益系数的精准操控则面临很大的挑战,在可见光和红外波段可以将半导体增益介质[76]融入到超表面中,或者对超表面进行染料或离子掺杂[81],在太赫兹和微波频段可以尝试借助光泵激发的石墨烯[168,188]、增益线圈[89]和补偿电路[189]等方法.然而,这些方法所能提供的增益系数往往较小,难以满足PT 对称超表面的设计需求,因此,目前这一研究方向的实验进展较小.

需要指出的是,散射模型中的奇异点的出现并不需要严格的PT 对称性,事实上,无源的纯损耗超表面系统也会出现奇异点,以及奇异点诱导的单向无反射等效应[167,190−197].例如,Gu 等[167]设计了一种纯损耗的等效PT 对称超表面,由上下两个嵌入在介质中的银环谐振器组成,通过改变入射角并调整上下银环谐振器的间距,也可以观察到奇异点诱导的单向无反射现象.Dong 等[190]设计了一种在横向上损耗单元与无损耗单元周期排布构成的非厄米超表面,实现了奇异点诱导的单向逆向反射(retro-reflection)效应.这些工作为充分有效利用电磁超表面中的损耗,扩展超表面的功能提供了新思路.

3.3 超表面中奇异点在传感和相位操控方面的应用

非厄米电磁超表面中的奇异点拥有丰富的物理性质及多种应用,除了上述的偏振操控与奇异点诱导的单向无反射等特性,还在其他方面具有重要的实际应用价值,如超灵敏传感[159,198−200]和相位操控[163,201−204].

在奇异点附近工作的传感器拥有很高的灵敏度,这源于奇异点的重要特性,即,一个N阶奇异点通常对应于一个开N次方的频率分裂量 ∆ω ∝ε1/N,其中,ε为参数空间中奇异点附近的微扰[92,98].一个二能级系统的奇异点是二阶的,即N=2,对于系统中极小的微扰,频率分裂量要大于传统的基于线性关系的传感器的频率分裂量(图8(a))[94],因此,奇异点传感的灵敏度更高.这一高灵敏特性在Park 等[198]设计的等离激元超表面中获得了验证(图8(b)).他们设计的超表面由上下两层在横向上错位的金条阵列组成,实验证明在奇异点下折射率灵敏度可达 4821 nm·RIU−1.奇异点传感的灵敏度随着阶数N的增大可以进一步提高,高阶奇异点可以在由多组元结构构建的多能级系统中获得[93].采用高阶奇异点可进一步放大微扰并实现更高的灵敏度增强,有望在折射率传感、温度传感、纳米颗粒检测、光学陀螺仪和生物化学传感等方面展现重要的应用价值.

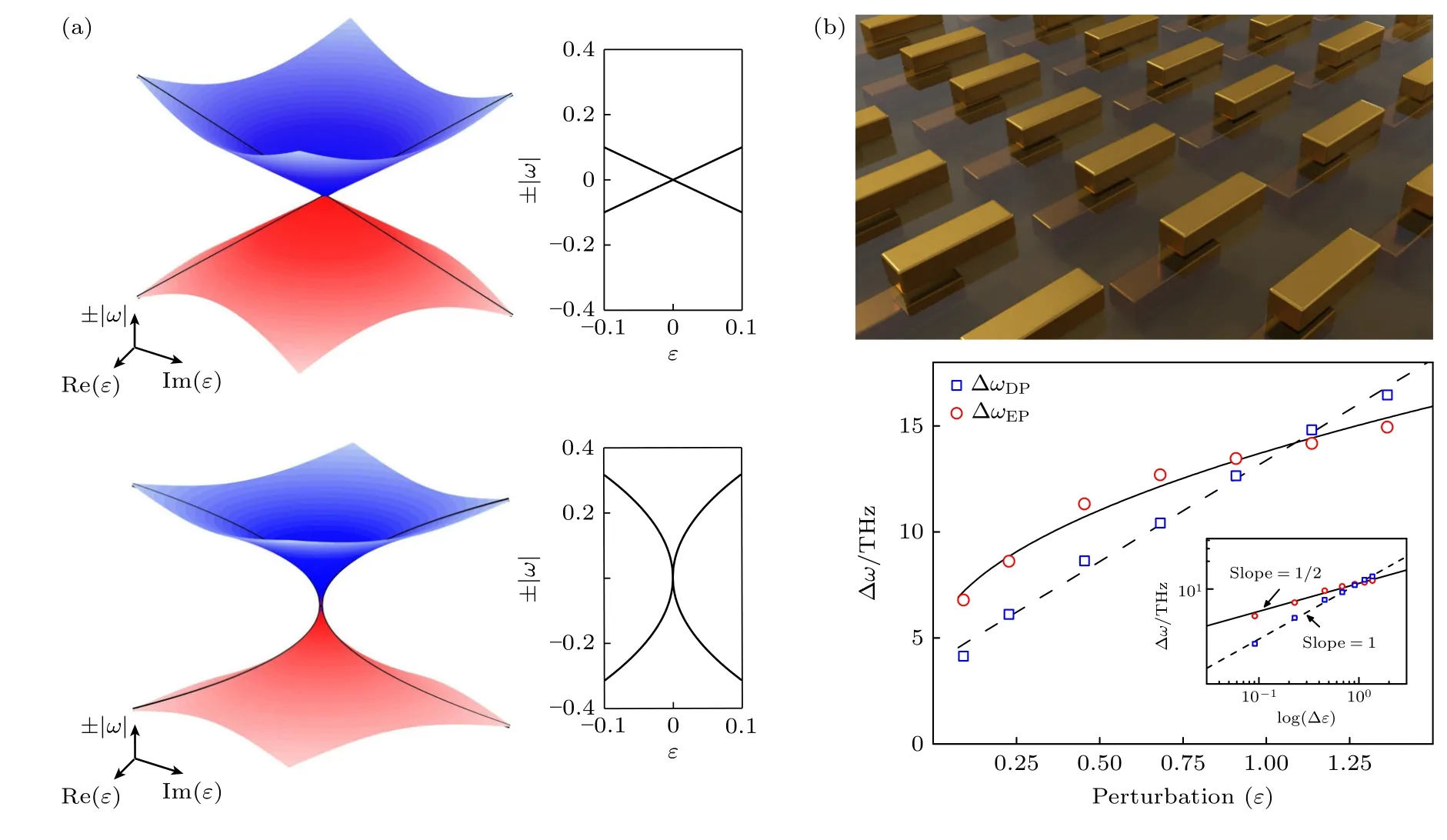
图8 非厄米超表面中奇异点在传感方面的应用 (a) 左: Diabolic 点(DP)的频率分裂量与微扰强度 ε 的关系;右: 奇异点的频率分裂量与微扰强度 ε 的关系[94];(b) 左: 由上下两层在横向上错位的金条阵列组成的等离激元超表面;右: 在奇异点下频率分裂量随微扰强度 ε 的变化[198]Fig.8.Sensing applications of EPs in non-Hermitian metasurfaces.(a) Left: Frequency splitting of DP versus the perturbation strength ε ;Right: Frequency splitting of EP versus the perturbation strength ε [94].(b) Left: A plasmonic metasurface composed of two layers of gold bars with a lateral shift;Right: The frequency splitting of EP versus the perturbation strength ε [198].

非厄米电磁超表面中奇异点的另一个重要的应用是相位操控.前文中提到,由于奇异点在参数空间中独特的拓扑结构,围绕奇异点的一个完整环路,本征态不会回到自身,而是相互交换,并积累π的几何相位,这一非厄米系统中奇异点的拓扑特性吸引了研究人员的广泛关注[163,201−204].Leung 等[163]设计了一种等离激元超表面(图9(a)左图),可用于产生涡旋光束,上层金膜刻蚀了相互垂直的狭槽,底层有与狭槽相同形状的金条,形成巴比涅互补图样[205].超表面的每一个单元都从超表面的中心区域开始沿着径向排布(图9(a)右图),这样的排布方式用以产生涡旋光束.研究发现,通过改变相互垂直的狭槽/金条之间的距离可调控耦合强度,在合适的间距下,奇异点就会出现,并伴随着交叉极化透射率为零.调节间距穿越奇异点时,远场的轨道将会旋转 45◦(图9(b)).另外,Song 等[202]将围绕奇异点产生的拓扑保护的相位差与Pancharatnam-Berry 相位结合,实现了圆偏振依赖的超表面全息.这些研究为偏振控制、结构光和全息等方面的新一代可调谐光子器件的设计提供了新思路.

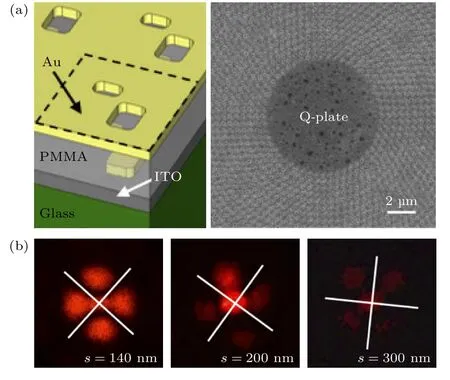
图9 非厄米超表面中奇异点在相位操控上的应用 (a) 左:超表面结构单元示意图;右: 实验样品照片图[163];(b) 实验测得的交叉偏振衍射图样随垂直狭槽的间距的变化[163]Fig.9.Phase control with EPs in non-Hermitian metasurfaces.(a) Left: illustration of the metasurface unit cell.Right: The photograph of the fricated sample[163].(b) Experimental cross-polarization diffraction patterns for different separation distance between orthogonal slots[163].

4 非厄米电磁超表面上的奇异表面波

表面波是一种局域在界面附近的电磁模式,其波矢要比同频率自由空间中的电磁波的波矢大,这一特性使得表面波在高度集成的光子器件的设计上有着非常广泛的应用[206].其中最重要的是表面等离激元波,它是自由电子与电磁场相互作用产生的沿金属表面传播的电子疏密波[206].在平直的金属表面上,表面等离激元波可沿平面上各个方向传播.为了控制表面等离激元波的传播方向,Correas-Serrano 等[108]提出了一种各向异性的等离激元超表面,该超表面拥有极端各向异性的电导率.这一非厄米超表面上的表面波的色散关系可推导为

其中σxx和σyy分别为超表面的电导率张量在x和y方向上的分量;Z0为真空阻抗;k0为真空中波数;kx,ky和kz分别为表面波的波矢在x,y和z方向上的分量.当y方向上的电导率趋于无穷大时,即Re(σyy)→±∞或 Im(σyy)→±∞,(15)式可以化简为

(16)式表明,在这种极端情况下,在kx-ky平面上的等频率曲线为一条沿着kx方向的直线.由于能流方向由等频率曲线的法线方向决定[207,208],因此超表面上的表面等离激元波将沿y方向传播,自准直效应即由此产生(图10(a)左图).Correas-Serrano 等[108]进一步采用石墨烯提出了一种各向异性等离激元超表面的设计方案(图10(a)右图).然而,在这样的纯损耗超表面上,表面波的能量会随着传播距离的增大而很快被耗散掉.受PT 对称系统中增益对损耗补偿作用的启发,Coppolaro等[110]提出了增益和损耗周期性调制的PT 对称超表面,获得了沿传播方向不衰减的自准直表面等离激元波.

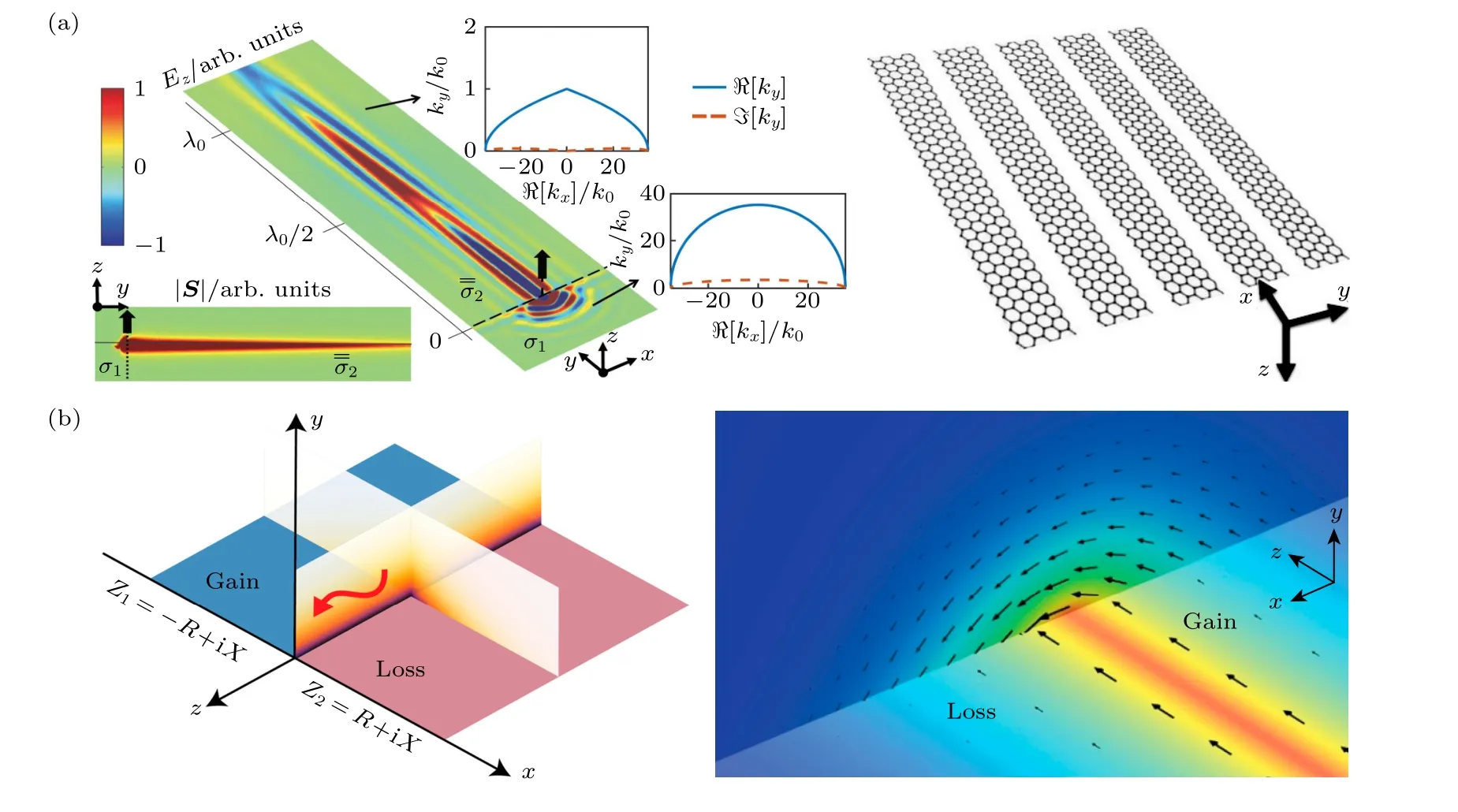
图10 非厄米电磁超表面上的奇异表面波 (a) 左: 各向异性非厄米超表面上的自准直表面等离激元波;右: 基于的石墨烯的设计的各向异性非厄米超表面[108];(b) 左: PT 对称超表面上的线波示意图;右: 线波的仿真结果[109]Fig.10.Extraordinary surface waves on non-Hermitian electromagnetic metasurfaces.(a) Left: Surface plasmon canalization on an anisotropic non-Hermitian metasurface;Right: The graphene-based anisotropic non-Hermitian metasurface[108].(b) Left: Line waves on a PT-symmetric metasurface.Right: The simulation results[109].

另一方面,线波(line wave)作为一种新型表面波,被发现于电感型和电容型这两个互补超表面的边界[209−211].不同于传统的沿着整个平面传播的二维表面波,线波是一种一维的表面波,具有强的场局域、大的工作带宽、方向依赖的偏振、鲁棒性强等特点.有趣的是,Moccia 等[109]研究发现,如果引入PT 对称性,线波可以存在于单一的电感型或电容型超表面上.他们设计了由两个拥有相同电感值(或电容值),但电阻值互为相反数的PT 对称超表面(图10(b)左图),其阻抗Z在空间中的分布满足如下关系式:

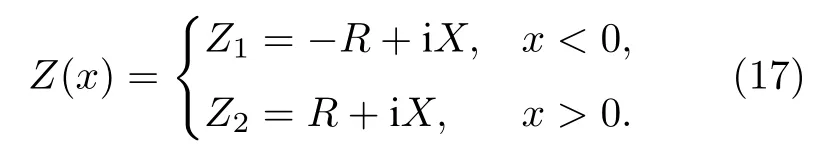
这里正电阻(R>0)表示损耗,负电阻(R<0)表示增益.正参数X(X >0)表示容抗,负参数X(X <0)表示电抗.从(17)式可以看出,阻抗Z在空间中的分布满足PT 对称条件,即

在这样的PT 对称超表面上,线波会出现在增益和损耗超表面的边界处,它不会沿传播方向衰减,这是因为从增益超表面一侧流出的电磁能量恰好补偿了损耗超表面一侧耗散的能量,这样的单向能流使得线波具有特定的手性(图10(b)右图),如果采用圆偏振源激发,可以产生波源手性依赖的单向传播线波.该项研究为新型光子集成与光学传感器的设计提供了新思路.

5 总结和展望

本文综述了近年来非厄米电磁超表面的发展现状.在传统超表面中,损耗往往是需要极力避免的不利因素,而非厄米物理可以将超表面中的损耗转变为一个新的设计自由度,为实现非常规物理效应,以及扩展超表面功能提供新方向.目前,非厄米电磁超表面已经在完美吸收、奇异点、奇异表面波等方面展现出了独特的物理性质与应用.未来,更多的新物理效应与新应用仍需进一步探索.例如,非厄米拓扑物理[212]、赝厄米物理[213]等新物理效应,以及片上集成非厄米超表面器件、可重构非厄米超表面器件、非厄米超构光栅[214−216]等新应用与新器件.需要指出的是,非厄米电磁超表面的发展对实验制造技术提出了更大的挑战.例如,作为非厄米超表面的重要应用之一,超灵敏传感,它的实现需要极高的制造精度[217].另一方面,PT 对称超表面要求严格平衡的增益与损耗,但要控制电磁材料的增益系数,并使其与损耗系数严格平衡是非常困难的,严格PT 对称电磁超表面的相关理论的实验验证进展缓慢.

简而言之,非厄米物理与电磁超表面的结合形成了新的交叉研究领域,这不仅为研究基础物理现象提供了一个新的平台,同时也有望在诸如电磁隐身、电磁屏蔽、超灵敏传感、光束操控和新型光子集成等方面展现重要的实际应用价值.