结合机器学习的大气压介质阻挡放电数值模拟研究*

艾飞 刘志兵 张远涛

(山东大学电气工程学院,济南 250014)

大气压介质阻挡放电是应用中常用的放电形式,通常使用等离子体流体模型进行理论描述.本文针对大气压均匀介质阻挡放电每半个电压周期出现一次或多次电流脉冲的特性,基于机器学习方法构造一个全连接多层神经网络,采用误差反向传播算法,并设计了一个通用的隐藏层结构,将计算数据或实验数据作为训练集,借助于人工神经网络程序研究大气压介质阻挡放电的电流密度、电子密度、离子密度和电场强度等宏观与微观放电特性.通过分析计算结果可知,在给定合适训练集的条件下,构造的机器学习程序与流体模型能以近乎相同的计算精度(误差小于2%)来描述大气压介质阻挡放电等离子体性质,同时计算效率远高于求解流体模型,并能极大地拓展放电参数的遍历范围.本文的算例表明,将机器学习程序与现有的流体模型或动理学模型结合起来,将极大地提高大气压放电等离子体的模拟效率与效果,深化对放电等离子体的认识.

1 引言

近年来,随着大气压下气体放电技术的发展,低温等离子体的应用在污染防治、杀毒灭菌、能源转化等领域有了长足的进步[1−3].在大气压下,放电系统可以摆脱真空装置的限制,应用更为方便,但由此也带来了更为多样性的边界过程,等离子体与待处理物的相互作用更为复杂[4].而且,工作气体也往往是反应性气体,放电过程中碰撞频繁,电离过程多是逐步进行的,产生大量的激发态和亚稳态粒子[5].比如空气、CO2、NH3中的反应,往往涉及到上百种粒子、上千个化学反应,从数值模拟的角度来讲,每增加一种粒子,就需要在流体模型中增加一个连续性方程来反映其演化[6−8].特别地,大气压下粒子的生存周期差别较大,甚至跨越纳秒量级到秒量级的多个量级,为了能准确反映每一种粒子的动态演化,对流体模拟的时间步长的选择提出了更高的要求,尤其当进行二维与三维计算时,流体模拟所需的计算工作量也是相当巨大的[9,10].当然,对于大气压微放电这种空间尺度在微米量级,与纳秒脉冲放电这种时间尺度在纳秒量级的放电过程,往往需要借助于动理学模型才能准确地理解其演化过程的动理学特性,多粒子种类与频繁碰撞将给大气压下的动理学模型带来极大的计算负担[11,12].可以说,随着大气压放电应用的进一步深入,对其放电性质的数值模拟研究也面临着诸多挑战.

当然,随着高性能计算技术的进一步发展,比如并行计算与图形处理器(graphics processing unit,GPU)计算的发展,都将极大地增强现有计算方法的模拟能力[13−15].近年来,随着大数据处理技术的发展,机器学习在物理学各个分支开始体现出其独特的优势[16],在聚变等离子体领域也已经有了相对成熟的应用[17,18],但是机器学习在低温等离子体研究中,特别是在低温等离子体的模拟中,还较少涉及[19].

机器学习(machine learning,ML)是人工智能的一个重要分支,其通过对大量数据的统计和分析自动获取数据间的对应关系[20,21].机器学习的基本思想是: 通过复杂系统的样本集来训练模型,从而基于大量数据预测或发现复杂系统的内在关系.得益于近年来计算能力的巨大进步,这种通过数据驱动实现复杂系统建模的思想已经在诸多应用方面成为现实,这也为在大数据的基础上研究等离子体特性奠定了客观基础[16,22].人工神经网络(artificial neural networks)是机器学习的重要分支[23−26],最近研究表明,具有多隐藏层的人工神经网络在复杂数据集模拟建模方面效果优异,是研究低温等离子体的合适工具[19,27,28].

因此,本文的主要目的是结合机器学习与流体模型,以大气压介质阻挡放电为例[29−32],讨论机器学习方法在放电等离子体研究中的计算效率与效果,探索机器学习方法在低温等离子体模拟中的进一步应用.本文首先详细描述了基于机器学习人工神经网络的低温等离子体数值模拟方法,并提出一个适用于本文等离子体模型的通用隐藏层结构;然后通过求解单一输入控制参数和多控制参数条件下氦气介质阻挡放电模型来证明该算法的有效性,将计算得到的电流密度、电子密度、离子密度和电场强度等放电特性与流体模型数据进行对比,表明机器学习方法可以应用于放电等离子体的研究,并比较了计算效率.

2 计算方法描述

通常情况下,流体模型是描述大气压放电等离子体的合适模型[29−34].一般用连续性方程来描述带电粒子与中性粒子的产生与消失,使用漂移-扩散近似来描述粒子的运动,泊松方程用来计算电场,电子能量守恒方程用于在麦克斯韦分布假设下计算电子温度[35−38].具体方程的一维形式如下:

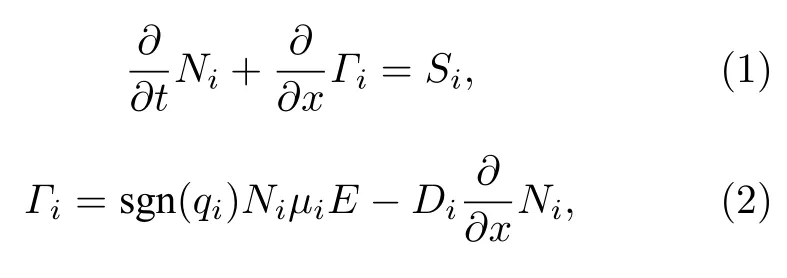
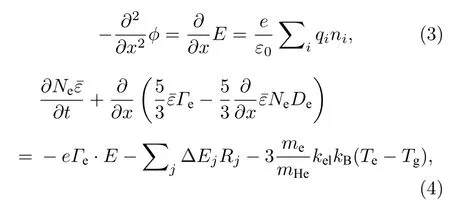
其中,i指第i种粒子,N和Γ指各种粒子的密度和通量,S指粒子源项,µ和D分别指迁移率和扩散系数.qi表示第i种粒子的电荷数,sgn(qi)是qi的符号.ϕ,E,e和ε0分别是电势、电场、基本电荷和真空介电常数.表示由给出的电子平均能量.∆Ej和Rj是相应反应j中电子碰撞的能量交换和相应的速率系数.kB,me,mHe,kel,Te和Tg分别是玻尔兹曼常数、电子质量、背景气体的分子质量、背景气体粒子与电子之间的碰撞频率、电子温度和背景气体温度.

本文使用的一维纯氦气介质阻挡放电流体模型所使用的参数包括放电间隙dgas为0.5 cm,覆盖电极表面的两个介质板厚度均为0.2 cm,相对介电常数ε为9.9.两个电极之间施加正弦电压v(t)=V0sin(2πft),其中,V0为幅值,f为频率.放电背景气体为纯氦气,反应集合来自文献[35].使用有限差分法数值求解上述方程(1)—(4),其中方程(2)结合改进的Scharfetter-Gummel (SG)算法.在当前使用的计算机硬件参数条件(中央处理器频率为3.00 GHz,内存为8.00 GB)下,大约施加10 个电压周期后放电达到稳定状态,针对不同的放电频率一般需要1520—4560 s 后,就可以提取数据用来讨论放电特性.

图1 所示是对于一个大气压纯氦气介质阻挡放电模型,采用流体模拟方法在外施电压幅值为2400 V、频率为10 kHz 时计算得到的电压数据和电流数据,与文献[39]结果相符.已有的研究表明,如图1 所示,大气压介质阻挡放电,严格讲是大气压介质阻挡放电在均匀放电模式下,在电压的上半周期,随着电压的增大,电流一开始近乎为零,当电压达到击穿电压后,发生放电,电流激增,放电空间的带电粒子被输运到介质表面并沉积下来,形成表面电荷,并产生与外加电场反向的附加电场,导致放电空间的电场很快低于击穿电场,放电电流迅速下降,一般形成一个脉宽几百纳秒到微秒量级的电流脉冲,同时产生大体积均匀的等离子体,当然在合适的电压与频率下也会出现多电流峰现象[30,31,40−43].从物理的角度看,大气压介质阻挡放电的电流曲线可以分为两部分: 一部分为电流几乎为零的未放电阶段,另一部分为快速变化的放电阶段.从数学的角度来看,这两部分的数学性质都是比较特殊的,在电流为0 的未放电阶段,其导数也近乎为0;在电流变化剧烈的放电阶段,导数极大,在最大值处导数为零(甚至是否可导也难以严格描述).而对于大气压射频放电而言,一般说来电流密度波形近似于光滑的正弦波形.可以说,大气压介质阻挡放电电流曲线的这种相对复杂的演化,为机器学习算法的引入带来了困难.

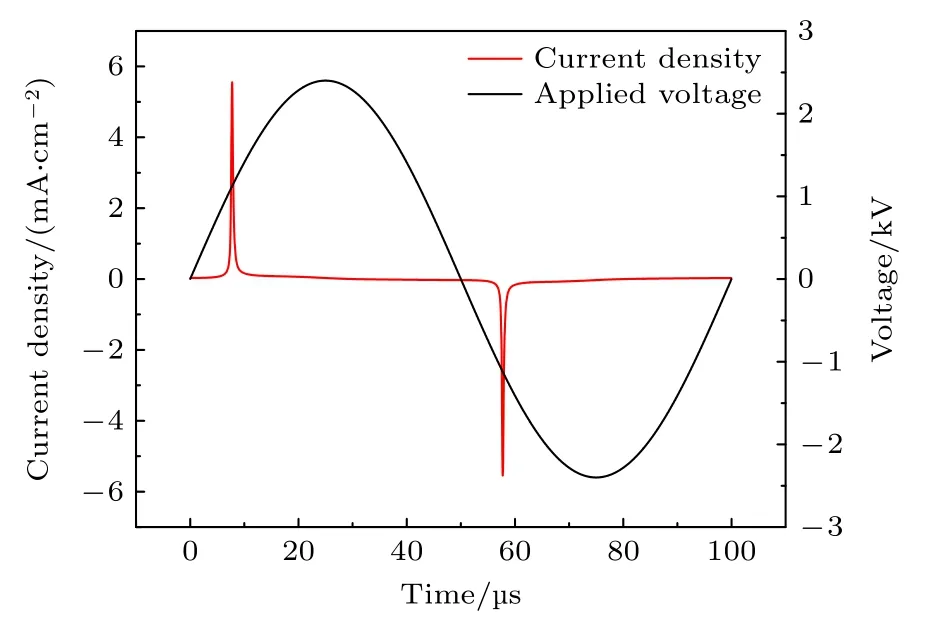
图1 训练数据Fig.1.Training data.

为了便于讨论,本研究仅限于每半个电压周期出现一次电流峰的情况,多电流峰情况将另文讨论.针对介质阻挡放电的电流曲线特性,为了准确获得电流密度,在神经网络程序的设计中,将一个周期均匀地分成4 部分,每四分之一周期都通过一个神经网络结构进行计算,用以精确反映相应的电流密度变化,这将有效提高计算的精度.如图2 所示,以单一输入控制参数(比如电压幅值)变化下求解介质阻挡放电模型的电流为例,针对上述电流演化的特点,本文构造了一个多层BP (back propagation)神经网络,其采用全连接模式[44].该网络输入周期数和电压值,输出电流密度,在搭建以及训练神经网络结构时,利用GPU 加速训练过程[45].在人工神经网络训练之前,其权重是随机初始化的.为了优化模型,构造了一个损失函数L1:

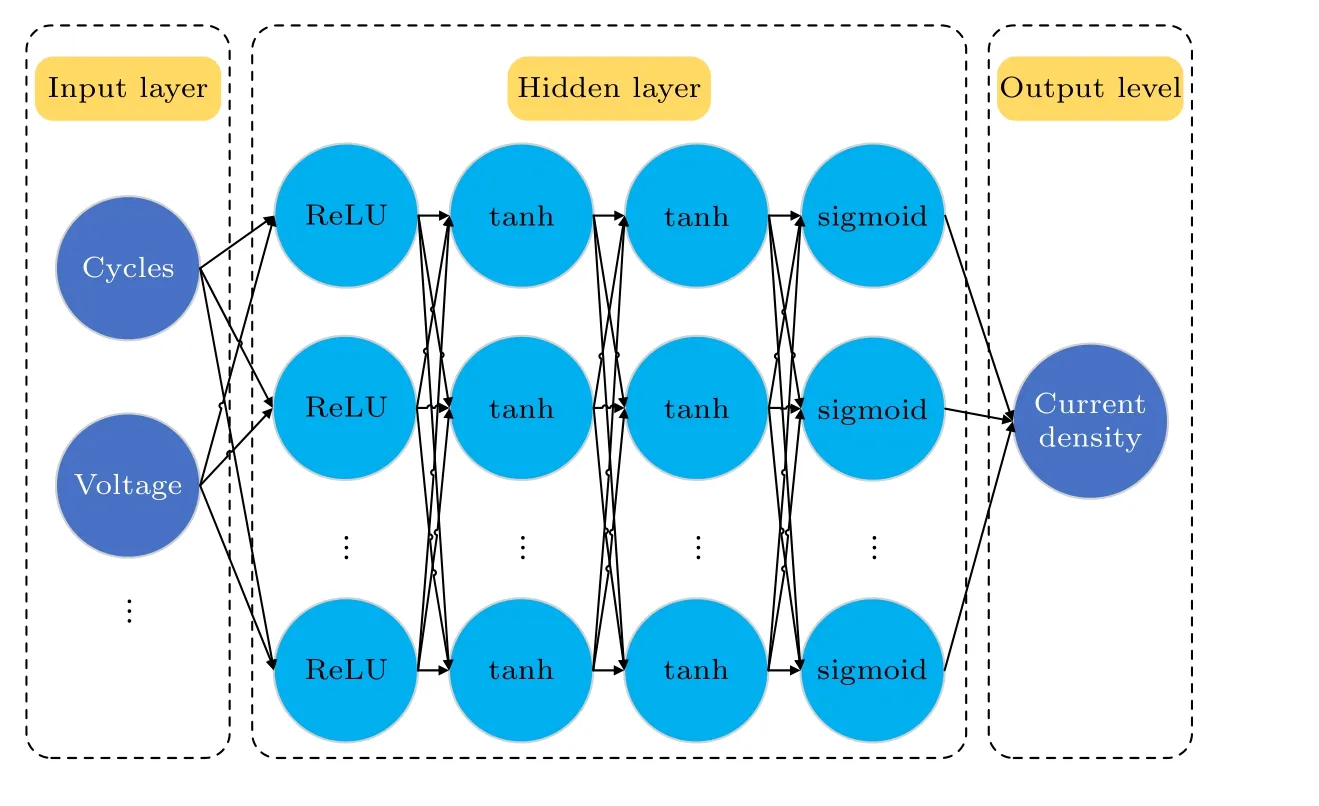
图2 基于大气压介质阻挡放电特性构造的人工神经网络图Fig.2.Diagram of artificial neural network constructed based on the characteristics of atmospheric pressure dielectric barrier discharge.

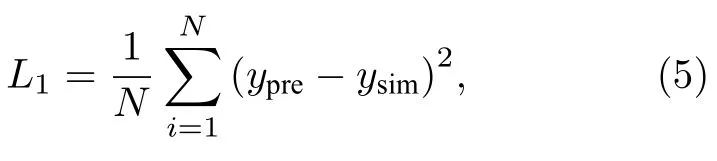
以测量人工神经网络的预测值和流体模型模拟值之间的差异.L1用于人工神经网络模型的训练迭代过程,通过最小化该损失函数,从而获得良好的神经网络.这里,N是在相应计算域中选择的散射点的数量,这些点构成训练集.ypre是人工神经网络的预测值,ysim是流体模型的模拟值.放电过程中的电流密度、电子密度、离子密度和电场强度都与电压有关,通过多次训练对比,同时考虑到通用性,构建了一个隐藏层结构.该隐藏层层数为4 且每个隐藏层均包含30 个神经元.本文神经网络选择了逻辑函数(sigmoid)、双曲正切函数(tanh)以及线性整流函数(ReLU)三种激活函数.其中,tanh和ReLU 可以更好地反映突变部分(如电流脉冲部分等),sigmoid 函数可以使得曲线整体更加平滑,通过多组激活函数的组合测试,最终4 层隐藏层依次使用ReLU,tanh,tanh,sigmoid 函数作为激活函数.对于电流密度,一个周期平均分为4 部分,采用4 个神经网络分别计算;对于电子密度、离子密度和电场强度,采用一个神经网络结构进行计算.最终计算结果表明,该结构可以较好地拟合电压幅值和多种放电特性之间的函数关系.

从机器学习算法的角度来看,增加输入参数,比如同时使用电压幅值与激励频率作为输入参数,将不可避免地增加对训练集数据量的需求,进而大大提高对计算设备性能的要求.对此,可以采取分批次训练的方法来减轻训练压力,在分批次训练时通常需要打乱训练数据,以提高训练的随机性,以便提高机器学习的预测效果.当输入参数增多后,比如可以进一步将放电间隙、介质层厚度、二次电子发射系数等参数作为输入属性加入模型,对模型复杂度要求也将进一步提高,如果发现现有模型结构不足以模拟输入输出的复杂关系时,便可以考虑适当增加隐藏层的神经元节点数,或增加隐藏层层数来更好地拟合输入输出,以便提高预测准确性.

为了方便不断完善训练数据集,扩大人工神经网络预测范围,可以设置一个相对较大的归一化范围,这可以方便在实验或计算获得新数据后对训练集的扩充,从而增大放电参数的遍历范围.当然训练集的数据类型的选择、训练集的数据质量、训练集数据量的大小等因素对最终的神经网络预测数据的准确性有重要的影响,这将另文讨论.

为了验证机器学习的预测效果,将流体模型得到的特定数据作为训练集.在单电流峰条件下,针对电压幅值变化的训练集由2000—2600 V 范围内,每隔20 V 选取一个作为训练数据,训练集中共有31 组不同电压幅值下的数据.考虑到电流密度等放电特性随频率变化的情况更加复杂,针对频率变化的训练集由10—30 kHz 每隔0.1 kHz 选取一个频率作为训练数据,训练集中共有201 组不同激励频率的数据.

将训练集代入人工神经网络进行训练,通过最小化损失函数L1来优化人工神经网络的权重.在训练过程中,采用了优化器Adam optimizer.优化器Adam optimizer 是目前最受欢迎的优化器之一,被广泛用于机器学习的优化迭代中,为了展示预测结果的准确性,构造了相对误差L2:

其中,N是在相应计算域中选择的散射点的数量,ypre是人工神经网络的预测值,ysim是流体模型的模拟值.相对误差L2可采用百分数的形式更加直观地展示出完成训练后的机器学习模型的预测值与流体模型模拟值之间的误差,用于验证机器学习方法的有效性.本文的人工神经网络是使用Python语言中的TensorFlow 框架实现的,TensorFlow是Google 的人工智能团队Google Brain 开发的一个开源且被广泛使用的机器学习库,其具有CPU(central processing unit)和GPU 版本,可以支持GPU 高性能数值计算.

3 结果与讨论

借助于流体模型来讨论均匀大气压介质阻挡放电的性质已经有了较多的讨论[29−32],本文所采用一维纯氦气介质阻挡放电模型及其离散化方法也经过了与实验数据的对比验证,具有一定可靠性和有效性[32,33,46].在流体模型提供的训练集的基础上,第2 节所构建的机器学习程序验证了在描述大气压介质阻挡放电特性方面的效率与效果.当然,如果实验数据合适,同样可以作为训练集代入上述机器学习模型中.另外,需要注意的是训练集是可以随着数据的不断获得而进一步扩充的,并不是必须要一次性获得一个完善的训练集(当然对训练集还是有一定要求的),随着更多的数据逐渐补充进入训练集,机器学习程序的预测能力将进一步增强[19].

3.1 电压幅值对放电的影响

在本文的计算中,训练集的数据来自流体模型,每个电压幅值对应的电压电流沿周期时间轴方向均匀采样约3341 个点作为训练数据,整体训练集中共有103571 条数据,经过训练后,机器学习程序就可以在给定电压值的条件下预测电流密度,预测结果如图3 所示,单个电压对应的电流密度所需平均计算时间为3.78 s,计算数据表明人工神经网络求解的电流密度与流体模型模拟结果差值很小,不论在未放电阶段还是在放电阶段.比如,在给定电压幅值为2150 (图3(a)),2250,2350 和2450 V (图3(b))情况下,机器学习程序与流体模型得到的相应电流密度值的差别分别为0.883%,0.577%,0.637%,0.518%.这表明,在经过训练后,机器学习程序完全可以用来准确给出放电电流值.

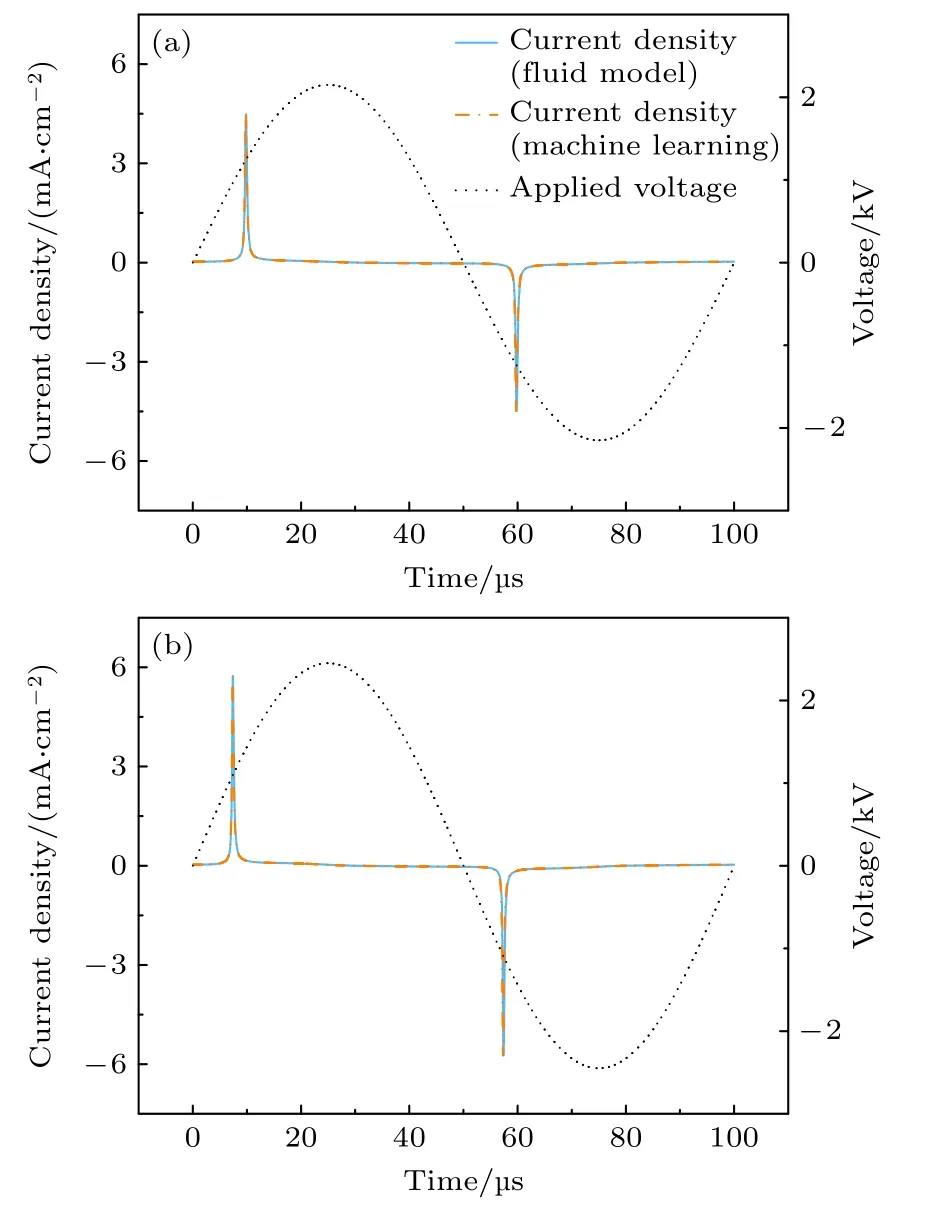
图3 通过机器学习预测He 等离子体在频率为10 kHz 下的电流密度,并与流体模拟的结果进行比较 (a) V0=2150 V 下的电流密度;(b) V0=2450 V 下的电流密度Fig.3.Prediction of current density of He plasma at ambient pressure (f=10 kHz) via machine learning with comparison of the results by fluid simulation: (a) Current density at ambient pressure (V0=2150 V);(b) current density at ambient pressure (V0=2450 V).

以外施电压的起始点作为零点,用机器学习方法计算出的给定电压正半周期的最大电流时刻分别为9.79,8.89,8.08 与7.37 µs.对应的电流密度峰值分别为4.51,4.93,5.35 与5.71 mA/cm2.由此可以看出,随着电压幅值的增大,电流密度峰值增大,且电流脉冲前移,更接近零点时刻.这与已知均匀大气压介质阻挡放电的性质一致[32].一般说来在保持单电流峰的前提下,正弦电压幅值越大,同一周期内电压数值增大越快,且更容易达到击穿电压,从而产生放电,放电电流也越强;同时,峰值时刻电子密度也更大,鞘层电场更强,如图4所示.图4 分别给出了基于机器学习与流体模拟得到的电流峰值时刻的电子密度、离子密度和电场分布.

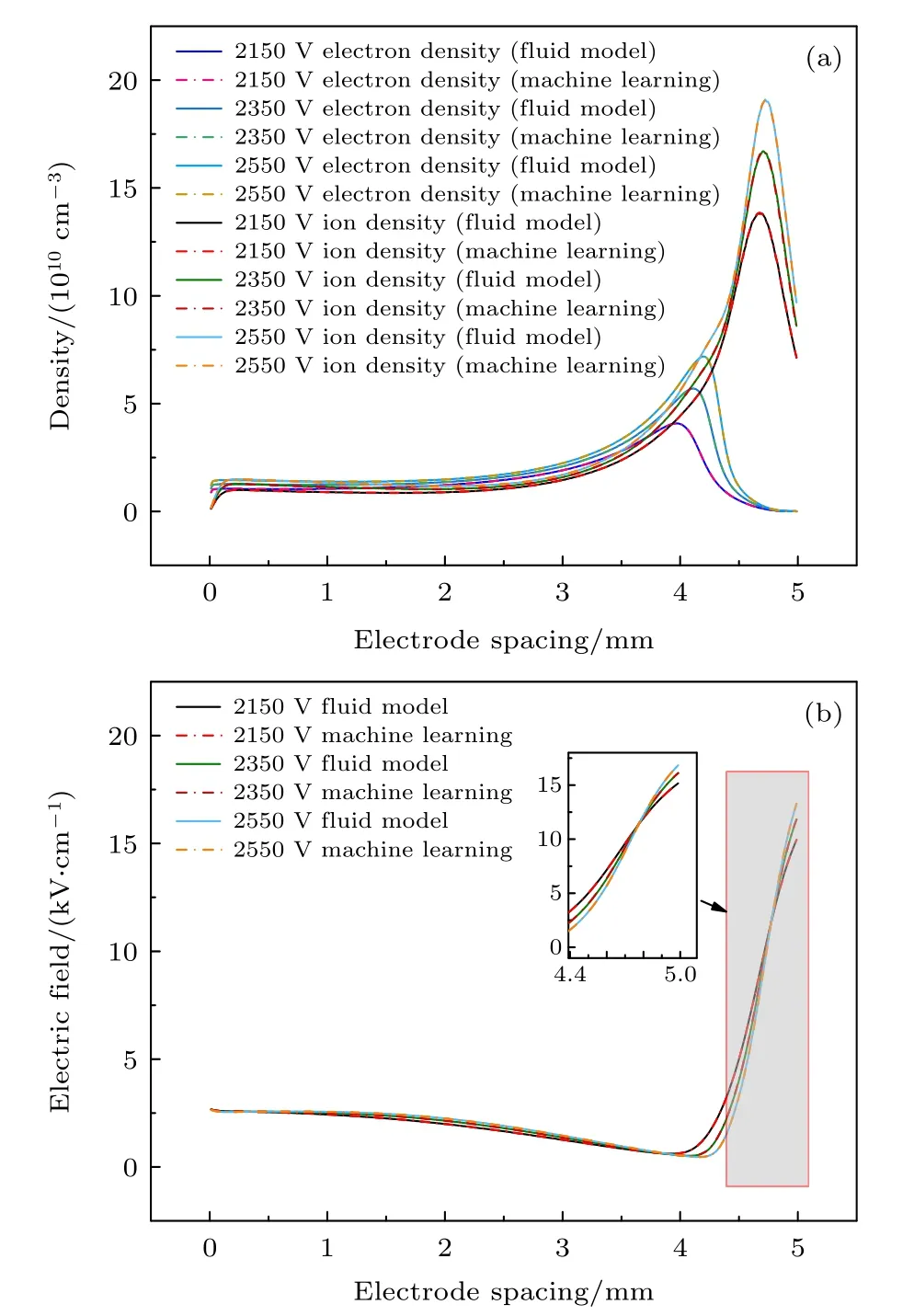
图4 通过机器学习预测He 等离子体在f=10 kHz 下的电子密度、离子密度和电场分布,并与流体模拟的结果进行比较 (a) 电子密度与离子密度;(b) 电场强度Fig.4.Prediction of electron density,ion density and electric field of He plasma at ambient pressure (f=10 kHz) via machine learning with comparison of the results by fluid simulation: (a) Electron density and ion density;(b) electric field.

每个电压幅值下的电子密度、离子密度和电场强度沿放电空间方向均匀采样449 个点作为训练数据,每个训练集中共有13919 条数据,单一电压对应的电子密度、离子密度和电场强度所需平均计算时间为3.64 s.从图4 可以看出,人工神经网络对于纯氦气介质阻挡放电模型电子密度、离子密度和电场强度也具有很好的预测能力.通过机器学习程序得到图4(a)中电子密度、离子密度和图4(b)中电场分布与流体模型数据的最大相对误差分别为0.283%,0.215%,0.0932%.从图4 还可以看出,即使在电子密度、离子密度和电场强度均剧烈变化的等离子体鞘层区内,神经网络的预测值同样能很好地拟合相应的数值和变化趋势.放电等离子体这些微观特性的预测进一步验证了机器学习程序的有效性.

如图5 和图6 所示,通过31 组不同电压等级下的数据构成训练集可以训练得到一个有效的神经网络结构,其能够快速准确地对10 kHz 下2000—2600 V 范围内的任意电压等级下的电流密度、电子密度、电场强度等进行预测计算,传统的流体模拟求解一组稳定的数据需要456 s (在给定的计算机硬件参数下),而采用机器学习的方法,计算输出所需时间均小于4 s,大大提高了计算效率.

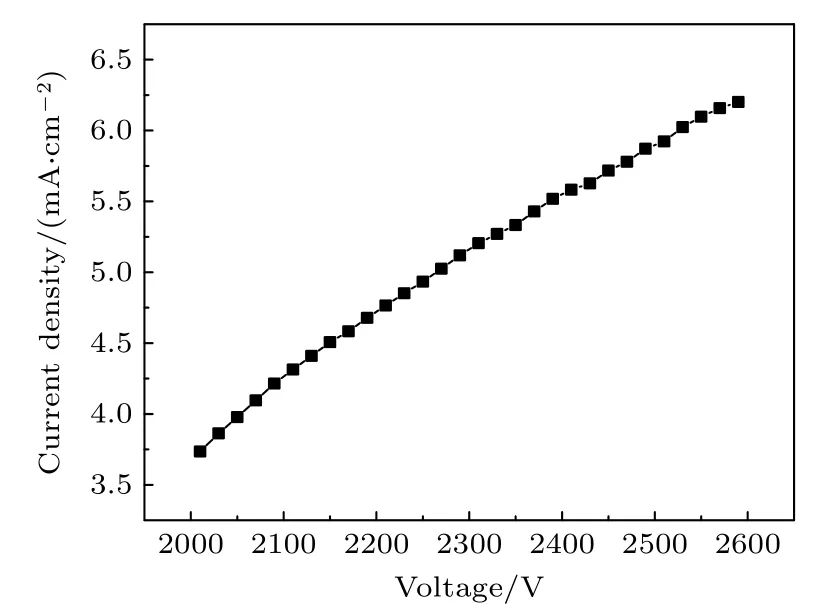
图5 电流密度峰值随电压幅值的变化Fig.5.Peak current density as a function of amplitude of applied voltage.

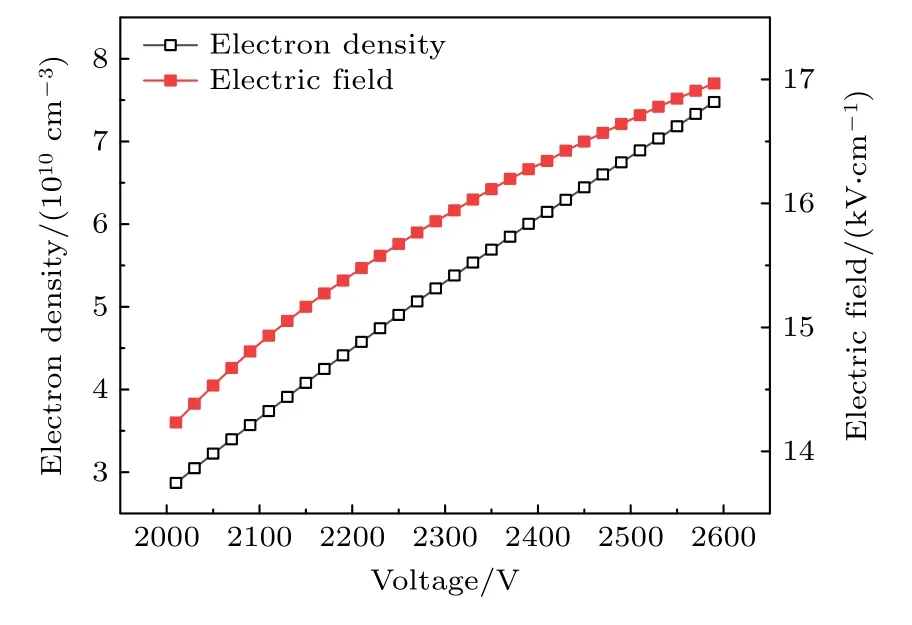
图6 电流密度峰值时刻的最大电子密度与最大电场强度随电压幅值的变化Fig.6.Maximum electron density and electric field at the moment when the current density gets to the peak value as a function of amplitude of applied voltage.

这就意味着,基于流体模拟程序给定的训练集,经过机器学习程序的分析和预测后,便可以快速地(至多几秒钟)得到给定范围内任意电压幅值下的电流密度、电场强度、电子离子密度等宏观与微观数据,不需要求解流体模型.图5 与图6 曲线上的数据点可以任意加细,也就是任给一个电压值,从图5 可以得到电流峰值,从图6 可以得到电场强度与电子密度峰值.

3.2 激励频率对放电的影响

不同外施电压激励频率下的电流密度如图7所示.在该模型下,训练集中每个电压频率对应的电流密度沿一个周期时间轴方向均匀采样约3341 个点作为训练数据,训练集中共有671504 条数据.从图7 可以看出,用机器学习求解的电流密度与流体模型模拟结果非常符合,单个电压对应的电流密度所需计算时间为3.71 s.即使在放电时刻电流密度变化剧烈,人工神经网络的预测值也能很好拟合.通过神经网络预测出的外施电压频率为14.05,19.05,24.05 和29.05 kHz 下的电流密度的相对误差L2分别为0.882%,0.435%,0.453%,0.425%.用机器学习方法计算出的正半周期的最大电流密度分别为5.98,7.30,7.66 与7.69 mA/cm2.由此可以看出,随着电压频率的增大,在单电流峰情况下,电流密度峰值会增大.考虑到机器学习程序更高的计算效率,显然便于遍历更广的参数范围,从而更好地分析放电的演化规律.

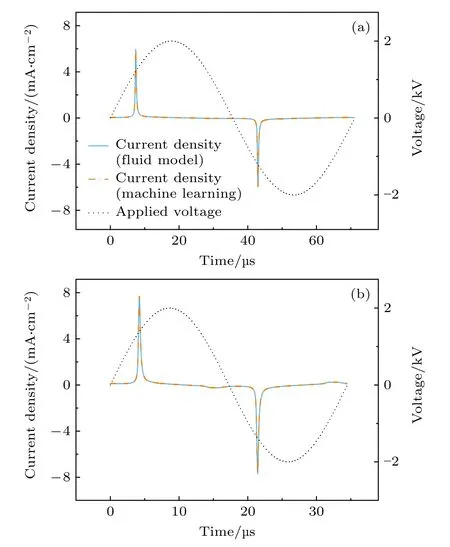
图7 通过机器学习预测He 等离子体在V0=2000 V 下的电流密度,并与流体模拟的结果进行比较 (a) f=14.05 kHz 下的电流密度;(b) f=29.05 kHz 下的电流密度Fig.7.Prediction of current density of He plasma at ambient pressure (V0=2000 V) via machine learning with comparison of the results by fluid simulation: (a) Current density at ambient pressure (f=14.05 kHz);(b) current density at ambient pressure (f=29.05 kHz).

同样地,可以借助于机器学习程序,进一步分析不同电压频率下电流峰值时刻的电子密度、离子密度和电场分布等微观特性,如图8 所示.

图8 通过机器学习预测He 等离子体在V0=2000 V 下的电子密度、离子密度和电场分布,并与流体模型模拟的结果进行比较 (a)电子密度与离子密度;(b) 电场强度Fig.8.Prediction of electron density,ion density and electric field of He plasma at ambient pressure (V0=2000 V)via machine learning with comparison of the results by fluid simulation: (a) Electron density and ion density;(b) electric field.

每个激励频率下的电流密度、离子密度和电场强度沿放电空间方向均匀采样449 个点作为训练数据,训练集中共有90249 条数据,单个电压频率对应的电子密度、离子密度和电场强度所需平均计算时间为3.68 s.从图8 可以看出,人工神经网络对于氦气介质阻挡放电的电流密度、离子密度和电场强度计算能力优秀,即使在等离子体鞘层区域电子密度、离子密度和电场强度均剧烈变化的情况下,神经网络也能准确地计算出放电参数的空间分布.图8(a)电子密度、离子密度和图8(b)电场分布的相对误差L2分别为0.631%,0.329%,0.159%.

如图9 和图10 所示,通过201 组不同频率下的数据构成的训练集可以训练得到一个有效的神经网络结构,其能够快速准确地对2000 V 下10—30 kHz 范围内的任意频率下的电流密度、电子密度、电场强度等进行预测计算,传统的流体模拟求解一组稳定的数据需要152—456 s,而采用机器学习的方法,计算输出所需时间均小于4 s,在保证计算效果的基础上大大提高了计算效率.

图9 不同频率下的电流密度峰值Fig.9.Peak current density at different frequencies.

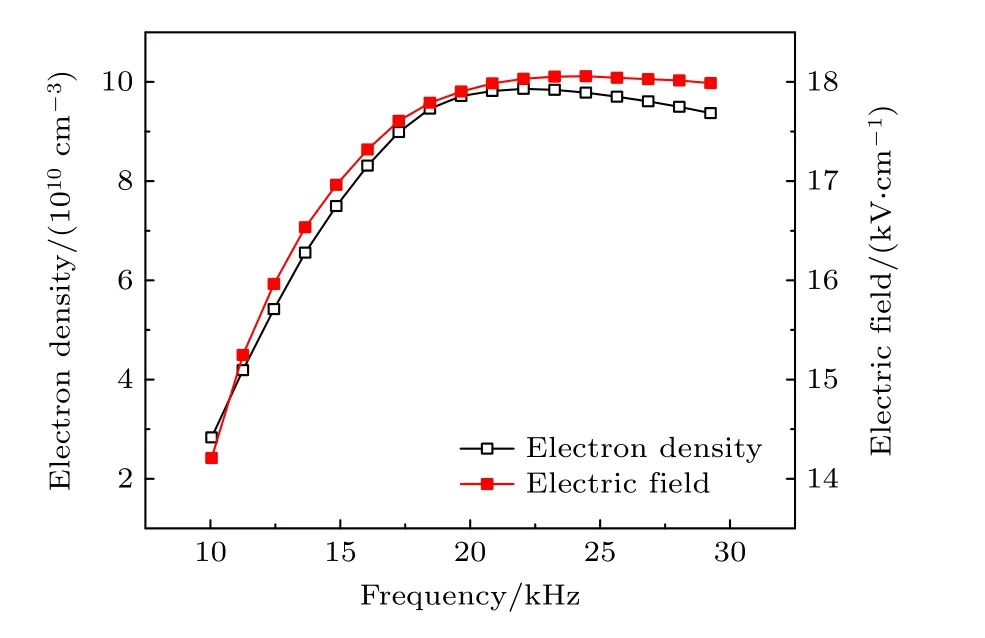
图10 不同频率下最大电流时刻的电子密度峰值和电场强度峰值Fig.10.Peak electron density and peak electric field intensity at the moment of maximum current at different frequencies.

3.3 电压幅值与激励频率同时对放电的影响

在实际的放电研究中,放电的控制参数除了电压幅值与激励频率外,还有放电间隙、介质层厚度、介电常数等,在机器学习中同时考虑更多的输入控制参数并没有本质的困难.

在构建的机器学习模型下,为了同时反映电压幅值和激励频率对放电特性的影响,电压幅值由2000—2600 V 每20 V 选取一个电压等级.同时,在上述每个电压幅值下,激励频率由10—30 kHz每0.1 kHz 选取一个频率构成训练集,训练集中共有6231 组不同外施电压下的数据.每个外施电压对应的一个周期内的电流密度沿时间轴方向均匀离散为约3341 个点,神经网络的训练集由20816624条数据组成.经过训练后,机器学习程序就具备了任意给定电压幅值与激励频率两个参数,快速给出大气压射频放电宏观与微观特性的能力.

图11 将激励频率为14.05 和29.05 kHz 时不同电压幅值下的电流密度的时间分布与流体模拟的结果进行了比较.显然,人工神经网络具有很好的预测能力,能够精确计算出在外施电压幅值和频率变化时电流密度的准确数值及其演化趋势.通过该模型计算出激励频率为14.05,19.05,24.05 和29.05 kHz 时2150,2350,2550 V 三个电压幅值对应的电流密度相对误差的平均值,分别为1.95%,1.49%,1.4%,0.976%,而计算一组数据所需时长为3.69 s.

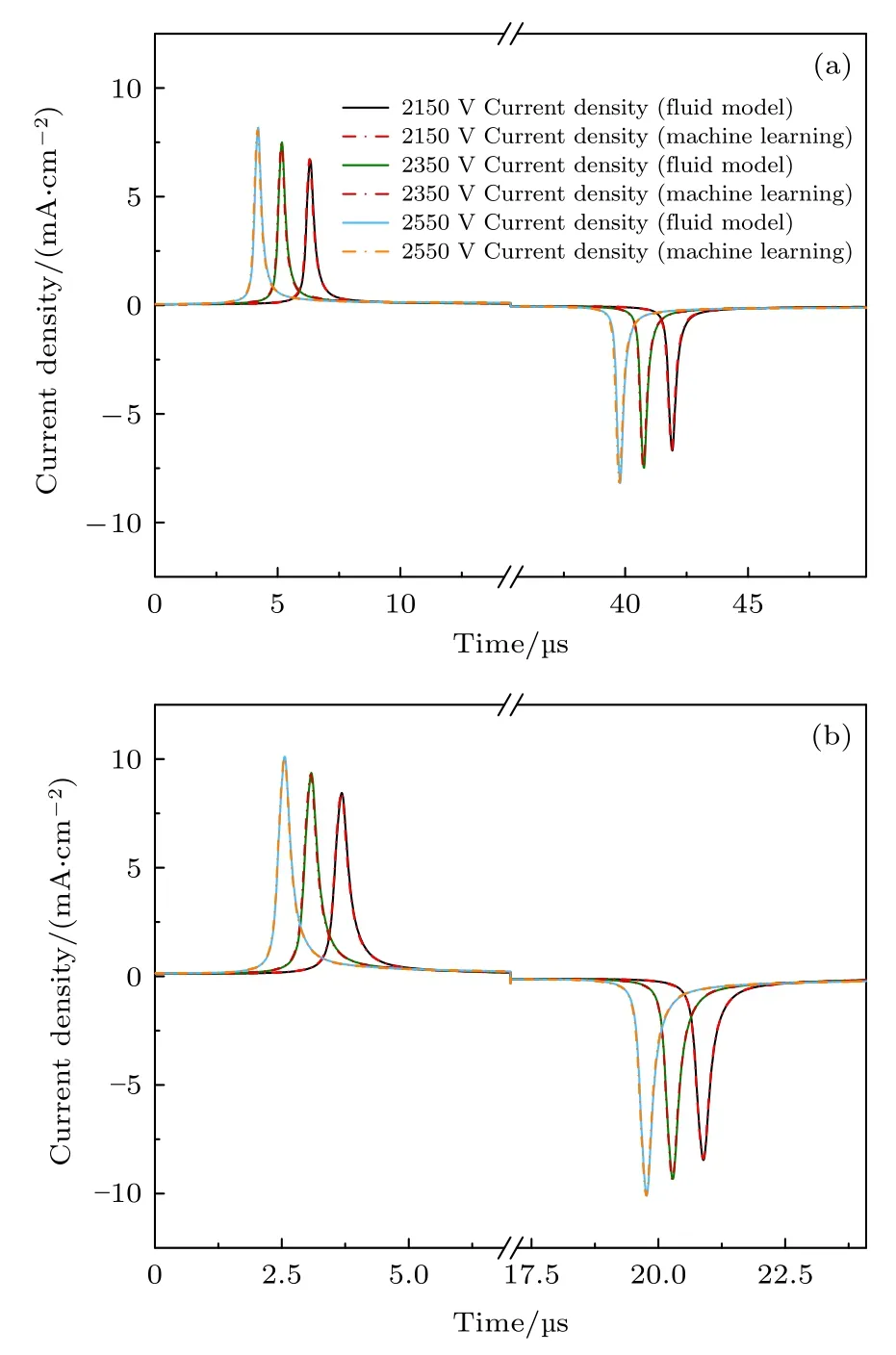
图11 通过机器学习预测He 等离子体在多输入属性变化下的电流密度,并与流体模拟的结果进行比较 (a) f=14.05 kHz 下的电流密度;(b) f=29.05 kHz 下的电流密度Fig.11.Prediction of current density of He plasma under the change of multi input attributes machine learning with comparison of the results by fluid simulation: (a) Current density at ambient pressure (f=14.05 kHz);(b) current density at ambient pressure (f=29.05 kHz).

为了同时考虑电压幅值与激励频率的变化,神经网络的训练集包含6231 组不同的外施电压(与本节电流密度模型相同),并将每个电压下的电子密度、离子密度和电场强度均匀离散为449 个点,在计算域中共产生2797719 条数据作为该模型的训练集.图12 和图13 分别给出了基于机器学习模型在不同电压幅值与激励频率下电流峰值时刻电子离子密度与电场强度的分布.从图12 和图13 中机器学习方法和流体模型的计算结果比较可以看出,人工神经网络具有良好的预测能力,能够对放电模型的电子密度、离子密度和电场强度进行准确的计算,同时也能正确反映出电压幅值变化时放电特性的变化趋势.

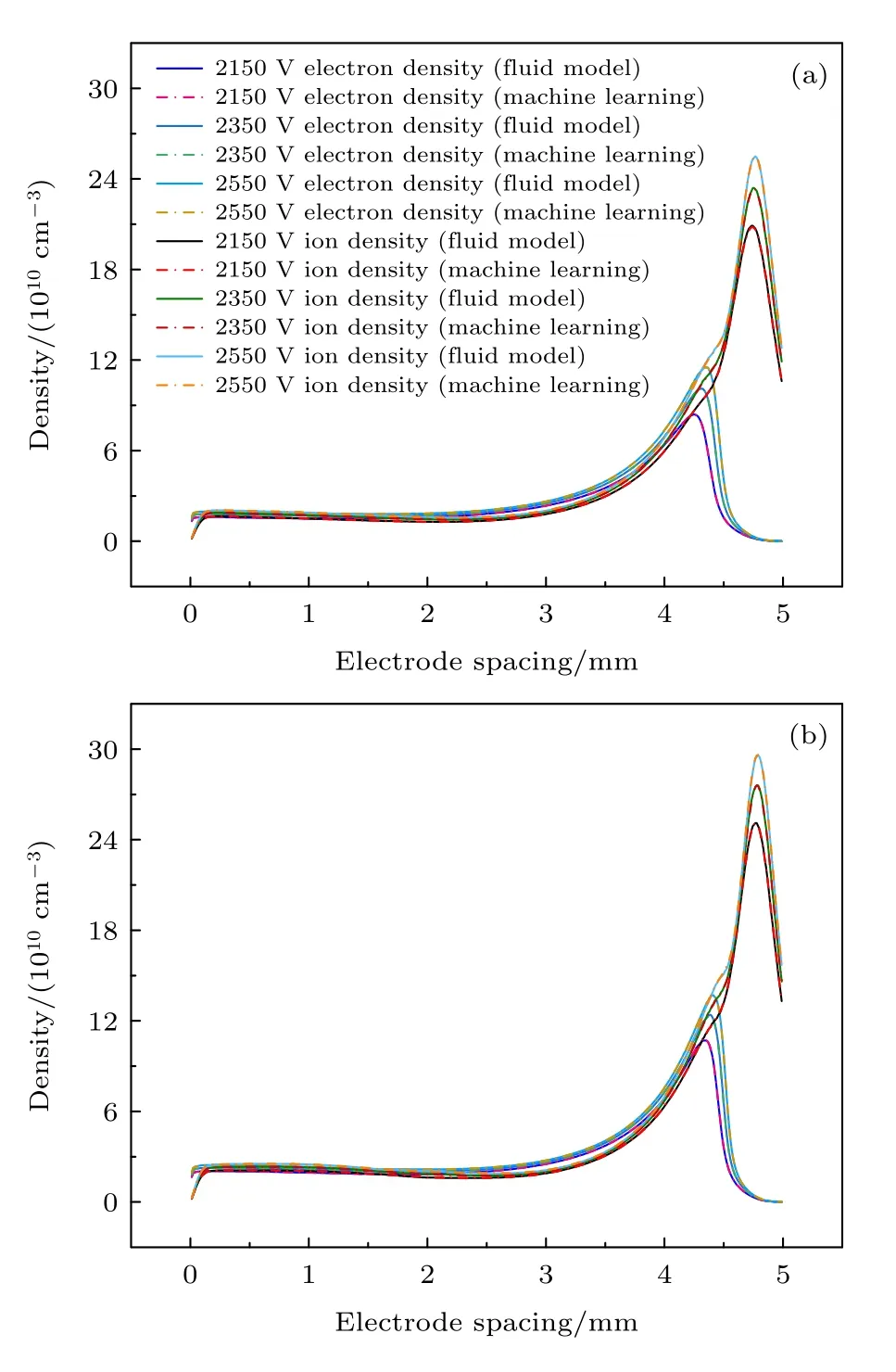
图12 通过机器学习预测He 等离子体在多输入属性变化下的电子密度和离子密度,并与流体模拟的结果进行比较 (a) f=14.05 kHz 的电子密度;(b) f=29.05 kHz 的离子密度Fig.12.Prediction of electron density and ion density of He plasma under the change of multi input attributes via machine learning with comparison of the results by fluid simulation: (a) Electron density at ambient pressure (f=14.05 kHz); (b) ion density at ambient pressure (f=29.05 kHz).

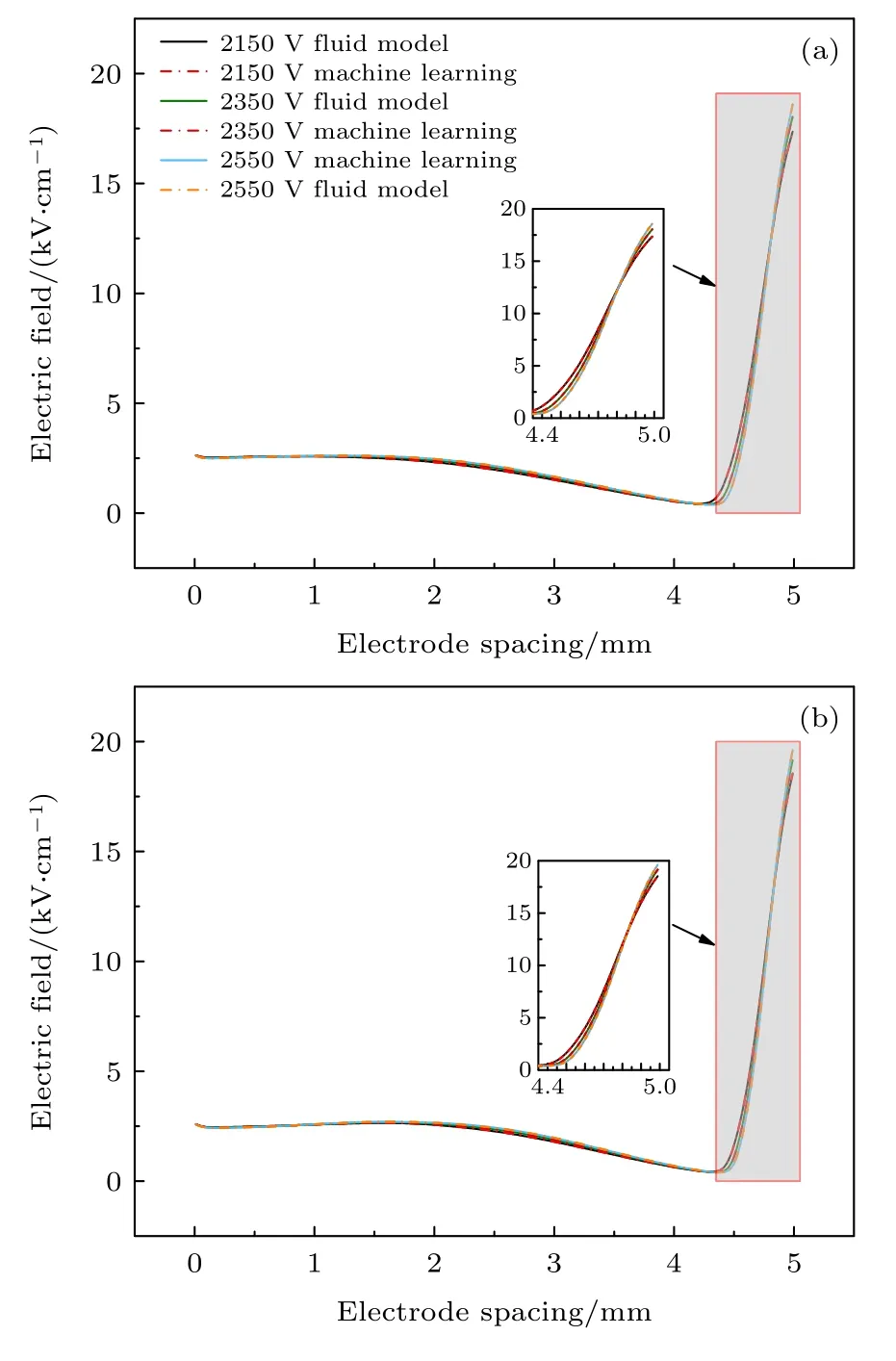
图13 通过机器学习预测He 等离子体在多输入参数变化下的电场强度分布,并与流体模拟的结果进行比较 (a) f=14.05 kHz 的场强分布;(b) f=29.05 kHz 的场强分布Fig.13.Prediction of electric field of He plasma under the change of multi input attributes via machine learning with comparison of the results by fluid simulation: (a) Electric field at ambient pressure (f=14.05 kHz);(b) electric field at ambient pressure (f=29.05 kHz).

在该模型下,如图12 所示,通过机器学习方法计算出的激励频率为14.05 kHz 时对应的不同电压幅值下的电子密度、离子密度的平均相对误差分别为0.449%和0.332%;激励频率为29.05 kHz时对应的电子密度、离子密度的平均相对误差分别为0.8%和0.447%.从图12 可以看出,在给定频率下随着电压幅值的增大,鞘层内的电子密度与离子密度均有所增大,同时两者构成的等离子体区的整体密度也略有增加[39,47].

值得指出的是,通过人工神经网络计算单一电压对应的电子密度、离子密度和场强所需时间约3.55 s,远小于相同计算设备条件下传统流体模型得到稳定数值所需要的152—456 s,可以说机器学习程序在确保计算精度的条件下,有效提高了放电特性的计算效率.

如图13 所示,在给定训练集的情形下,通过机器学习方法计算出的激励频率为14.05 kHz 时对应的不同电压幅值下的电场强度的平均相对误差仅为0.228%;激励频率为29.05 kHz 时的电场强度的平均相对误差仅为0.208%.从图13 可以看出,在给定频率下,随着电压的增大,在单电流峰情况下,鞘层峰值电场逐渐增大,鞘层宽度基本稳定,略有收缩,这均符合已有的大气压介质阻挡放电规律[39,47].

从以电压幅值与电压频率两个放电参数的机器学习程序可以看到,当继续增加诸如放电间隙、介质层厚度、介质层类型等放电参数后,如果有合适的训练集,同样可以构建合适的机器学习程序(如上所述,这并不存在本质的困难),从而从理论上可以实现任给一个或者多个放电控制参数,就可立即得到诸如电流、电场、电子密度、离子密度等放电宏观与微观特性.即任给一个放电参数集合,就可以基于机器学习程序,而不是求解流体模型或者动理学模型,立刻得到放电等离子体特性.

4 结论与展望

近年来,机器学习的方法在不同的物理分支研究中发挥着越来越重要的作用,在聚变等离子体的研究中已经有相对广泛和成熟的应用,然而在低温放电等离子体的研究中还较少使用.本文提出在流体模型的基础上辅以机器学习方法,以大气压介质阻挡放电为例研究放电等离子体的性质.计算表明,通过已有的流体模型或实验数据得到训练集,引入机器学习方法,可以快速地预测电流密度、电场强度、电子密度等放电等离子体宏观与微观特征.在本文研究氦气大气压介质阻挡放电中,基于现有的计算设备,流体模型通常需要152—456 s得到一组稳定的数据,而经过训练后的机器学习程序则可以在少于4 s 的情况下,以相同的精度(误差小于2%)得到相应的数据.当然从另一个角度来看,如果能通过实验获得足够多的数据,代入本文构造的神经网络程序中,同样可以有效分析与预测放电等离子体的特性.

另外,借助于机器学习程序也可以极大扩展参数的计算范围,遍历参数范围受限往往被认为是数值计算的重要缺陷之一.通常情况下,在借助于流体模型进行计算的时候,由于放电参数的变化,计算程序的时空网格选取需要手动或者自适应的改变,计算程序可能会出现不稳定、不收敛、数值溢出、计算中断等众多问题.引入机器学习的方法将有效改变这种情况,借助于流体模型得出的“相对有限”的训练集,代入到机器学习程序,就可以在给定的范围内准确预测其他放电控制参数下的数据,得到“近乎无限”的放电宏观与微观数据集,这对于研究放电参数对放电演化的影响具有重要意义,特别是在通常的数值模拟不能遍历较大参数范围的情况下.从这个角度讲,在大气压下将动理学模型与机器学习方法结合起来可能更有意义,本课题组也正在进行相关的研究,以期在大气压下结合动理学模型与机器学习更好地研究大气压放电的动理学特性.