BP神经网络PID自适应控制悬架平顺性研究
刘省标,李 美,张少波,王德志
(海南大学机电学院,海南 海口 570228)
1 引言
悬架系统的作用是传递车轮与车架之间的力和力矩,汽车行驶时吸收路面对车辆产生的冲击与振动,其性能的好坏是影响车辆平顺性的关键。在悬架的发展过程中,被动悬架由于其刚度和阻尼不能调控,逐渐被能根据路面与汽车行驶状态实时调节的半主动悬架替代,因此对悬架系统控制策略的研究成为重点。
文献[1−2]利用PID控制在1∕4悬架模型中进行了对比仿真,提高了行驶平顺性,而常规PID控制效果取决于控制参数的选取,对非线性、时变的悬架系统进行控制时,参数整定时间长、不易实时调整且参数间相互影响导致控制效果不佳。神经网络具有通过数据自我学习、非线性映射、分布式信息存储、并行计算、容错能力强等优点,已在数据挖掘、模式识别、智能控制等领域得到广泛应用[3]。将神经网络应用在悬架系统控制中,能有效提高系统的实时性与鲁棒性,改善车辆的平顺性。文献[4]采用遗传算法对目标函数进行优化,将模糊控制器得到的最优输出数据作为导师信号供神经网络学习,使悬架平顺性提高;文献[5]采用RBF神经网络和PID相结合的方法研究C级路面上悬架系统对车身姿态的影响,提高了乘坐舒适性;文献[6]将粒子群优化算法应用于动态神经网络的训练,并将这种非线性控制方法与被动悬架和PID控制悬架进行对比分析。
证实了其有效性与鲁棒性,但是少见将BP神经网络与PID控制相结合的控制算法应用于悬架平顺性分析,此控制算法抗干扰能力强,具有良好的鲁棒性和自适应能力,适用于长期处于路面干扰下的悬架系统。
2 系统模型的建立
2.1 1/4车辆模型
根当前后轴的振动干涉不大时[7]研究在不平路面匀速行驶车辆悬架系统的动力学特性,可通过二自由度1∕4半主动悬架模型进行模拟和分析,如图1所示。
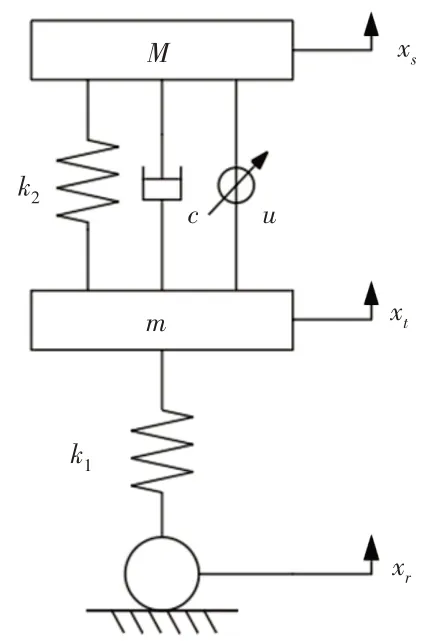
图1 二自由度1∕4半主动悬架模型Fig.1 2−DOF Dynamic Model of 1∕4 Semi−Active Suspension
图中:M、m—簧上、簧下质量;xr—路面激励;xt、xs—簧下、簧上质量质心的垂直位移;c—悬架等效阻尼;k1—轮胎等效刚度;k2—悬架刚度;u—作动器主动控制力。
2.2 半主动悬架状态空间模型

2.3 路面激励输入模型
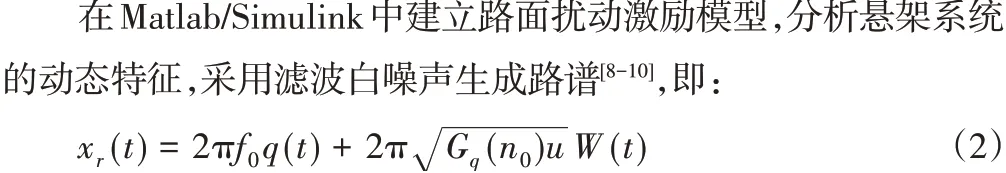
由式(2)在Matlab∕Simulink 中搭建B级路面谱的仿真模型,得到的滤波白噪声输入模型,如图2所示。
图2 滤波白噪声输入模型Fig.2 Input Model of Filtered White Noise
3 控制方法
3.1 PID控制器
PID控制是一种线性控制方式,控制器由比例单元(P)、积分单元(I)和微分单元(D)组成,形成控制量中相互配合又相互制约的关系,能够对被控对象进行闭环控制以达到满意的控制效果。其控制规律为:
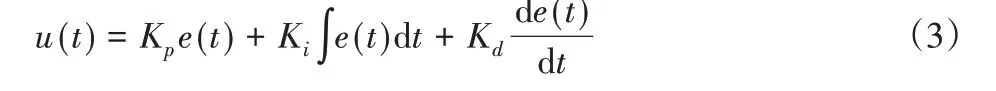
式中:e(t) =r(t) −y(t);Kp—比例系数;Ki—积分系数;Kd—微分系数。
在期望值r(t)和实际输出值y(t)之间存在偏差e(t),经线性组合后得到控制量u(t)对悬架系统进行控制,要求控制的实际输出值y(t)尽量接近期望值r(t),其控制流程,如图3所示。
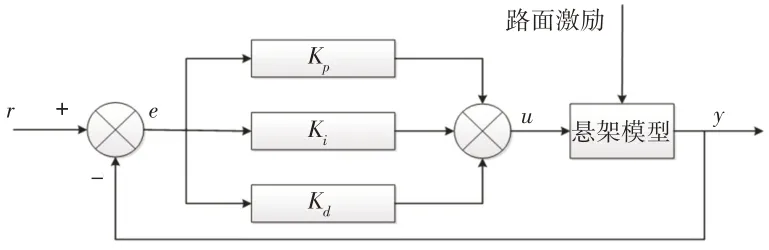
图3 PID控制器原理Fig.3 Priciple of PID Controller
在PID控制器中可通过调节Kp、Ki、Kd三个参数使其对悬架系统的控制效果达到最佳,采取试凑法对其参数进行整定,经多次仿真表明Kp= 500,Ki= 95,Kd= 0.5 时最大超调量、调整时间、稳态误差均可达到系统要求。
3.2 BP神经网络PID自适应控制器
利用BP神经网络建立Kp、Ki、Kd自学习的PID控制,可实现参数自行整定,以实现具有最佳组合的PID控制,其结构,如图4所示。
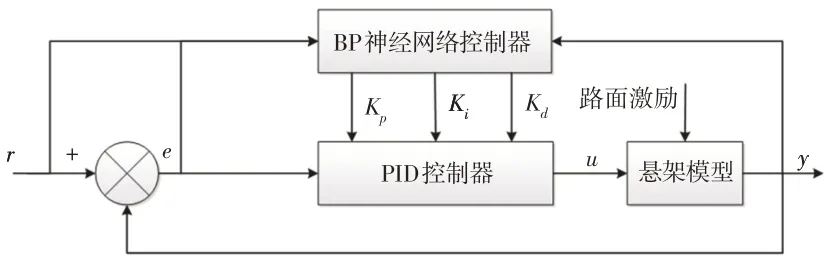
图4 基于BP神经网络的PID自适应控制系统结构Fig.4 PID Adaptive Control System Based on BP Neural Network

BP神经网络结构,如图5所示。采用输入层、隐含层、输出层三层前馈网络。输入层节点对应悬架系统运行状态量,为准确反映输入PID 控制器信号的特性,选取四个节点,x1=e(k),x2=e(k)−e(k−1 ),x3=e(k)−e(k−1 )+e(k−2),x4=du(k−1 ),其中,x1表示误差量,x2表示误差变化的快慢,x3表示x2变化的快慢,x4是控制器前一时刻的输出。
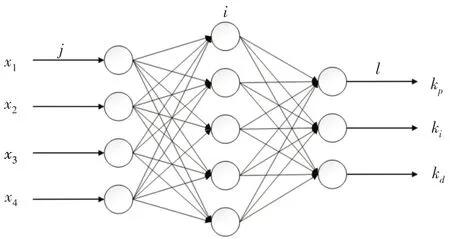
图5 BP神经网络结构图Fig.5 BP−Neural Network Structure
为充分保证神经网络的逼近能力、泛化能力以及收敛速度,隐含层节点选为五个。输出层神经元活化函数取非负的Sigmoid函数,其节点分别对应PID控制器的三个参数。

用梯度下降法修正神经网络的加权系数,并附加一个使搜索快速收敛到全局极小的惯性项,可得输出层权值计算表达式,如式(11)。
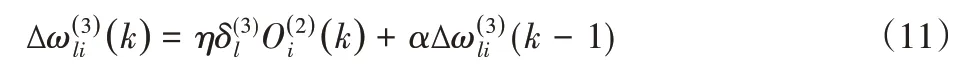
式中:η—学习速率;α—惯性系数。选取学习速率η= 0.1[11],惯性系数α= 0.1。
4 仿真及分析
4.1 仿真模型的建立
根据上述算法,在Matlab∕Simulink中搭建半主动悬架系统模型,如图6所示。以某型客车为研究对象对悬架系统平顺性进行仿真,其车型参数,如表1所示。
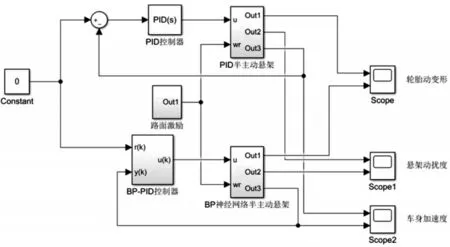
图6 BP神经网络PID自适应控制半主动悬架仿真模型Fig.6 Simulation Model of Semi−Active Suspension with PID Adaptive Control Based on BP−Neural Network
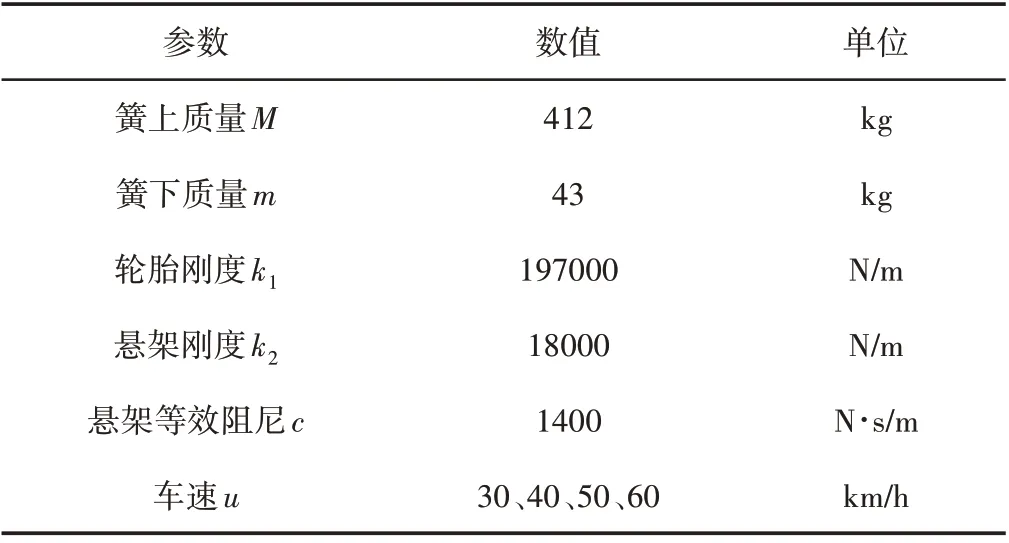
表1 车型参数Tab.1 Parameters of Vehicle
4.2 结果分析
在白噪声路面扰动激励下,分别对不同车速下的PID控制半主动悬架以及BP神经网络PID自适应控制半主动悬架的动态特性进行分析与仿真,当车速u= 30km∕h时,仿真结果,如图7~图9所示。

图7 轮胎动变形仿真曲线Fig.7 Dynamic Deformation of Tire Simulation Curve
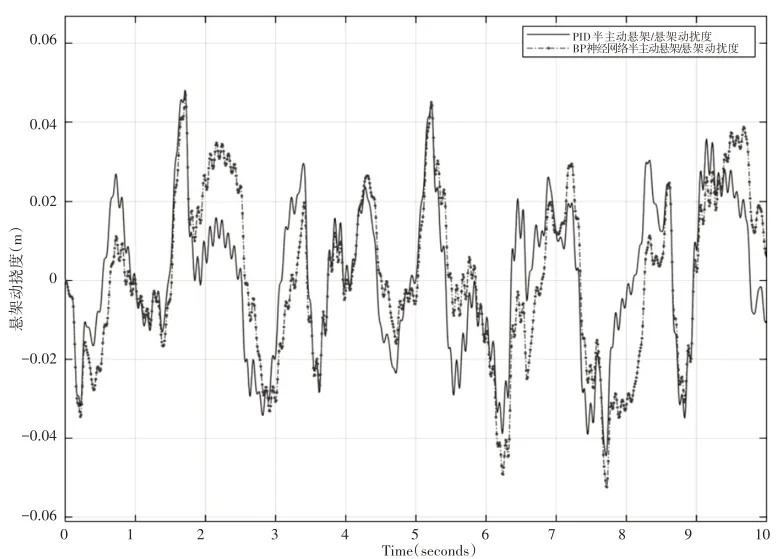
图8 悬架动挠度仿真曲线Fig.8 Dynamic Deformation of Suspension Simulation Curve
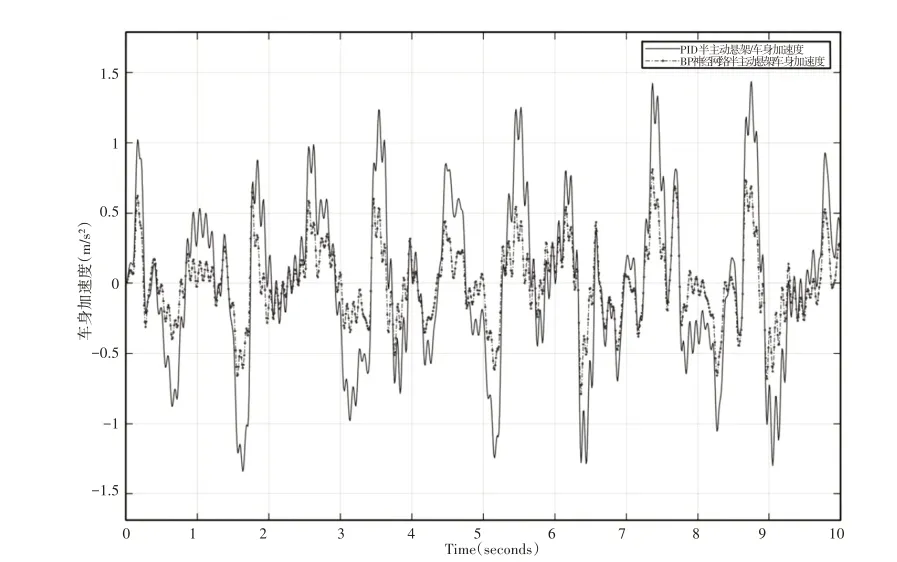
图9 车身加速度仿真曲线Fig.9 Vihicle Body Acceleration Simulation Curve
分别对车速u=30km∕h、40km∕h、50km∕h、60km∕h 的工况进行仿真分析,得到的各个评价指标的均方根值,如表2~表4所示。

表2 轮胎动变形均方根Tab.2 Dynamic Deformation of Tire RMS
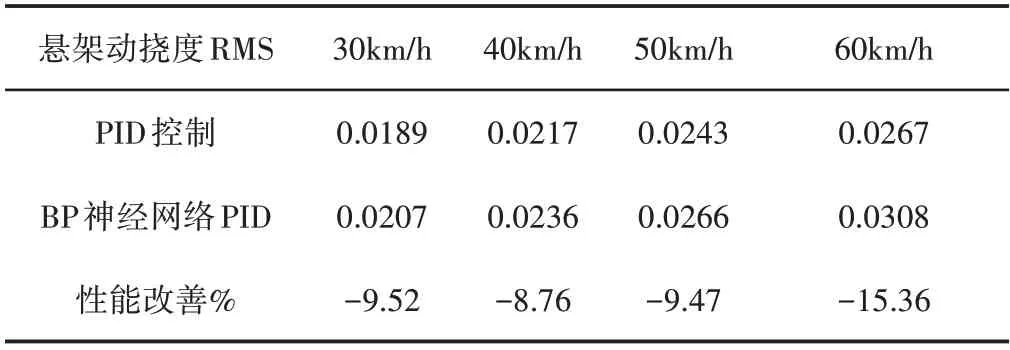
表3 悬架动挠度均方根Tab.3 Dynamic Deflection of Suspension RMS
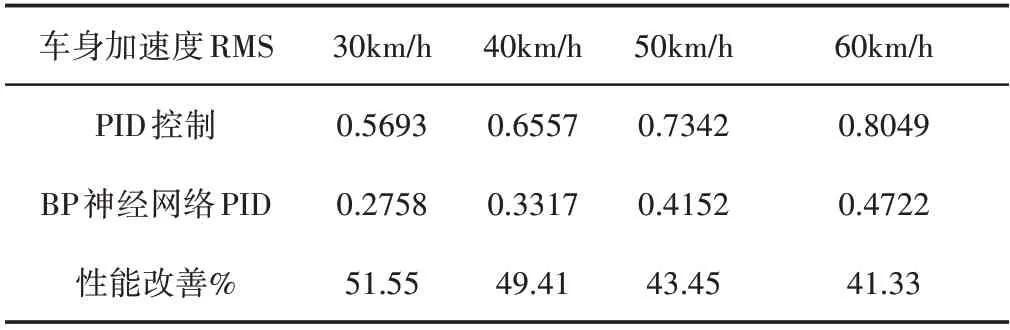
表4 车身加速度均方根Tab.4 Vehicle Body Acceleration RMS
由表2~表4 可以看出:相对于PID 控制,采用BP 神经网络PID自适应控制半主动悬架平顺性得到一定程度的优化,30km∕h时,轮胎动变形均方根比于PID半主动悬架降低了约14.47%,车身加速度均方根降低了约51.55%,有效的抑制了车身的振动,提高了汽车的平顺性,悬架动挠度略微增大了约9.52%。此外,车辆在不同车速的工况下优化效果略有不同。
5 总结
采用Matlab∕Simulink对车辆悬架系统进行仿真,对汽车悬架系统进行动力学分析,建立了1∕4半主动悬架的二自由度动力学模型。引用增量式PID控制器,采用三层前馈网络结构,设计BP神经网络PID自适应控制器。以某客车为研究对象,在白噪声路面扰动激励下,采用BP神经网络PID自适应控制策略对半主动悬架进行振动控制,与PID半主动悬架的性能指标进行了对比分析,结果表明:应用BP神经网络PID自适应控制的半主动悬架能更有效的抑制振动,车身加速度等评价指标得到了有效优化,整体波动幅度减小,使悬架系统具有更强的鲁棒性和自适应能力,能更好的满足车辆平顺性要求。

