基于OCSVM的燃气轮机叶片断裂故障诊断方法
江志农,党 伟,胡明辉,冯 坤
(1.北京化工大学发动机健康监控及网络化教育部重点实验室,北京 100029;2.北京化工大学高端机械装备健康监控与自愈化北京市重点实验室,北京 100029)
1 引言
燃气轮机具有运行平稳、结构紧凑、热效率高、启动速度快等优点,在舰船、石化管道等行业具有广泛应用。叶片作为燃气轮机的关键部件,据统计,叶片故障占叶轮机械故障总数的65%以上[1]。随燃气轮机载荷的提高,叶型和内部流场更加复杂,叶片损坏概率更大。燃气轮机一旦发生叶片断裂故障,不仅会导致机组性能下降,甚至会打伤转子其它部件或机匣,严重威胁燃气轮机的安全运行。目前我国主要是根据机匣振动速度有效值变化趋势监测机组状态,但存在以下问题:振动速度有效值为低频参数,主要频率成分为转子工频及二倍频,因此只有断裂叶片严重影响转子平衡状态后才能引起该参数变化。因此拟结合叶片振动机理,提取叶片断裂故障特征参数,建立叶片断裂故障诊断模型,解决上述问题。
目前国内外主要开展了以下两方面的研究:(1)基于有限元软件,建立叶片模型,分析正常和故障叶片的区别。文献[2]对叶片丢失激励下转子的动力学特性进行分析和试验,表明叶片丢失具有冲击特征,不平衡载荷产生突增。文献[3−4]建立叶片有限元模型,提出可根据固有频率的变化判断叶片是否存在裂纹故障且根据固有频率的变化量确定叶片损伤程度。文献[5]给出基于燃气轮机机匣振动信号和转速信号的叶片固有频率估计公式。(2)基于叶片信号利用信号处理方法识别叶片状态。文献[6−7]利用小波分解识别叶片的状态。文献[8−9]提出并利用实验数据验证转子的瞬时旋转角速度值可作为叶片根部松动、裂纹故障的特征参数。文献[10]基于风机叶片声发射信号,利用BP神经网络识别叶片故障。文献[11]利用多层感知机、等机器算法识别燃气轮机叶片的状态。
根据叶片固有频率变化分析叶片状态,该方法在实际应用中仍存在如下问题:(1)需经过模态测试确定每级叶片的固有频率,同时每型燃机需单独进行模态测试,导致该方法难以实际应用。(2)振动测点通常位于燃气轮机外机匣表面,叶片固有频率振动经过转子、轴承等复杂路径传递后,信号中包含大量无关成分,传感器很难检测到叶片的固有频率。故综上两点工程实际中很难通过监测叶片固有频率的变化识别叶片故障。目前形成的基于小波分解和神经网络的叶片状态识别方法,未充分考虑叶片断裂故障机理,且需要大量实际故障案例数据对模型进行训练,但对于燃气轮机叶片断裂类故障,现场故障数据很少。综上考虑,本文基于燃气轮机叶片尾流激振力产生机理,提出可监测的叶片断裂故障特征参数,建立基于OCSVM的叶片故障识别模型;将上述识别模型与转子叶片断裂引发的转子突发不平衡故障的诊断规则相结合,构建燃气轮机叶片断裂故障诊断方法。利用实际燃气轮机叶片断裂故障案例数据,验证提出的特征参数和诊断方法的有效性。
2 叶片尾流激振力产生机理
叶片尾流激振力产生机理,如图1所示。燃气轮机由于叶片尾缘、支板和附面层等的影响,在叶栅出口气流速度产生亏损,尾迹区的气流速度亏损可达(40~50)%,导致叶盘出口截面气流速度v、总压P沿周向脉动。此外在非均匀叶栅中由于叶盘安装角、栅距等参数不同,同样导致叶片通道面积和气流出口角度不均匀。而现代燃气轮机结构设计紧凑,一般前后两级动静叶盘间的轴向距离仅占叶片宽度的(10~15)%,导致由尾迹引起的气流速度分布凹坑无法恢复,在下级叶栅前缘截面压力、流速等仍沿周向分布不均匀,流场产生周向畸变。静子与转子叶片相对转动,下级叶栅受到由上级叶栅产生的周期性气体激振力作用[12]。图1中:P—稳态气体压力;ΔP——尾流激振引起的压力波动;u—燃气轮机转子转速。
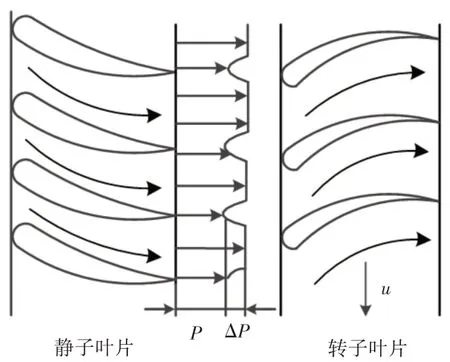
图1 尾流激振力产生原理示意图Fig.1 Schematic Diagram of Wake−Induced Vibration Force Generation
由燃气轮机叶片尾流激振力产生机理可得:
(1)燃气轮机气体激振力频率如式(1):

式中:K—燃气轮机构造系数,如叶片、支板、幅板等数量;fr—燃气轮机转子工频。
(2)燃气轮机转子动叶片受到气体激振力频率为上级静子叶片产生的静叶通过频率,静叶通过频率为静叶叶片数乘以转子工频;静子叶片受到的气体激振力频率为上级转子叶片产生的动叶通过频率,转子动叶叶片通过频率为动叶叶片数乘以转子工频。
(3)气体激振力为燃气轮机叶片的主要激振源,即周向气体脉动形成的周期性压力作用在下级叶片的工作面上,对叶片施以交变的激振力。
叶片受到的气体激振力如式(2):

式中:A—有效受力面积。
3 叶片断裂故障特征参数
燃气轮机实际运行过程中,压气机转子叶片主要受到离心载荷和气动载荷,静子叶片主要受到气体激振力作用,故转子动叶片受到的应力相对更大,发生断裂故障的概率更高。因此针对燃气轮机压气机转子叶片断裂故障,提取叶片断裂故障特征参数。
3.1 叶片通过频率幅值
燃气轮机压气机转子叶片断裂后,断裂级叶片的有效受力面积A减小,压气机气动性能下降,下一级静子叶片前缘的气体压力P下降。根据式(2)可得,叶片断裂导致叶片受到的气体激振力下降,故气体激振力产生的振动响应减小,即叶片通过频率幅值会产生突变。因此提取燃气轮机各级转子叶片通过频率幅值作为转子叶片断裂故障的特征参数之一。
3.2 转子工频幅值
假设燃气轮机转子原始不平衡量很小,转子叶片断裂导致转子不平衡量突增,转子受到突发不平衡激励作用,动力学特性发生变化。转子叶片断裂后,叶盘产生突加不平衡激振力Fr=mllΩ2,式中:ml—断裂叶片质量;l—叶片断裂前后叶盘质心变化距离;Ω—转子转速。
单盘转子不平衡量为l时,振动响应幅值r如式(3):
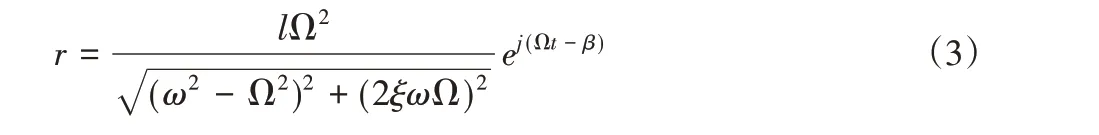
式中:ω—固有频率;ξ—阻尼比;β—转子振动相位;t—时间。由式(3)可得转子不平衡振动响应幅值r与不平衡量l成正比,燃气轮机叶片断裂导致转子不平衡量l改变,则转子的振动响应幅值在叶片断裂前后会产生突变。故提取燃气轮机转子工频幅值作为转子叶片断裂故障的特征参数之一。
3.3 转子工频相对相位
燃气轮机转子叶片断裂后,转子重心位置发生变化,振动相位会产生突变。但对于燃气轮机、航空发动机等复杂旋转设备,难以准确测量和计算转子的实际振动相位。由于燃气轮机同一截面水平、垂直方向的结构特性不同,导致转子发生故障时,不同方向的振动相位突变量不同。故本文选取燃气轮机同一截面水平、垂直方向同类型振动传感器转子工频的相对相位作为叶片断裂故障的特征参数之一,其中利用互功率谱计算转子工频相位。互功率谱密度函数描述了频域上两个信号间的相关性,可保留两信号间的相位信息,是一种抗干扰能力强、计算精度高、无需整周期采样的相位检测方法。利用互功率谱计算含N个点的振动信号x(t)中频率分量fo的振动相位,具体步骤如下:
(1)构建频率为fo、相位为0、幅值为1、长度为N的标准正弦信号y(t) = sin( 2πfot)。

4 叶片断裂故障识别方法
考虑到实际应用中叶片断裂案例数据获取较难,同时一台燃气轮机的不同级上出现叶片断裂时故障特征不尽相同,如果需要选用故障数据进行故障识别模型的训练,就需要获取各级叶片断裂的故障样本才能保证模型识别准确率,显然这在实际应用中难以实现。
因此,故障识别模型需要实现二分类,即叶片未断裂和叶片断裂,但训练样本尽量只需用叶片未断裂的样本,即使用单类样本进行训练实现二分类。正是考虑到这个工程需求,选用OCS⁃VM方法进行故障识别模型的搭建。
4.1 单分类支持向量机
Schölkopf 基于支持向量机的分离超平面和最大分类间隔思想,提出单分类支持向量机(OCSVM),将单分类问题转化为一个特殊的二分类问题,目标为寻找样本与原点间隔的最大分类超平面[13]。
OCSVM的优化问题如式(4):


式中:x、x′—样本;gamma—高斯核宽度。gamma和惩罚因子C直接影响支持向量机的分类精度和泛化能力,故采用粒子群算法对参数C和gamma进行寻优。
4.2 粒子群算法
粒子群优化算法(PSO)是一种启发式全局搜索算法,通过群体中个体间的协作和信息共享来寻找最优解[14]。PSO随机初始化粒子群,每个粒子在搜索范围内的最优解,记为当前粒子极值(pbest),将整个粒子群中的最优个体极值作为本次粒子群的全局最优解(gbest)。粒子群利用式(8)、式(9)更新速度和位置:

式中:Gk—寻优最高迭代次数;ωini—初始惯性因子;ωend—最高迭代次数时的惯性因子(一般取ωini= 0.9,ωend= 0.4);g—已迭代次数。
4.3 叶片断裂故障诊断模型
基于提取的叶片通过频率幅值、工频幅值和相对相位等敏感特征参数,结合单分类支持向量机,建立的燃气轮机叶片断裂故障诊断方法,如图2所示。
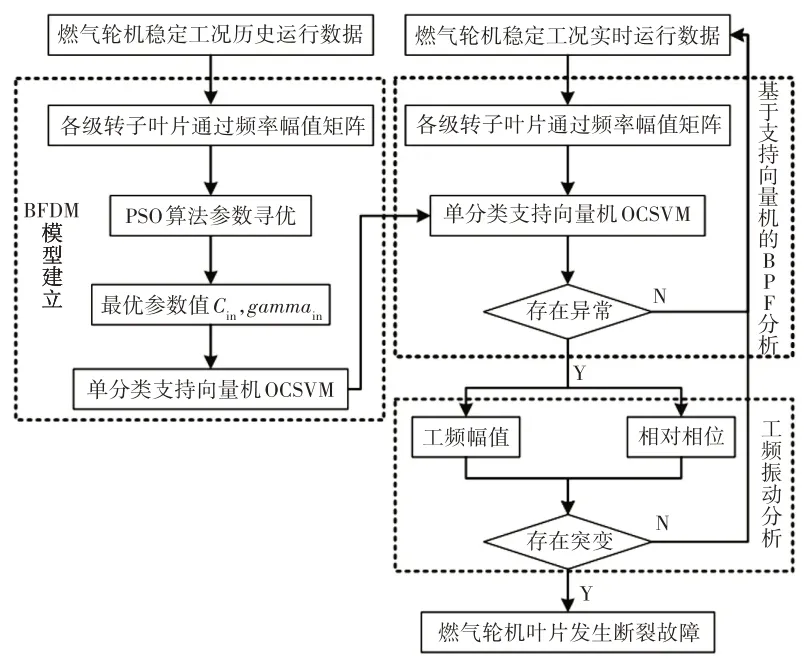
图2 燃气轮机叶片断裂故障诊断方法Fig.2 Fault Diagnosis Method for Gas Turbine Blade Fracture
具体步骤如下:
(1)在同一工况下,基于未发生叶片断裂故障数据构造多组转子叶片通过频率幅值矩阵。使用该矩阵进行单分类支持向量机OCSVM的训练,同时使用粒子群寻优算法对OCSVM的控制参数C、gamma进行寻优,进而建立基于OCSVM的叶片状态分析模型。
(2)对燃机的不同运行工况分别做第一步计算,进而获得各个工况下的叶片状态分析模型。
(3)对待分析数据进行各级转子叶片通过频率幅值的提取,获得转子叶片通过频率幅值矩阵,同时对其工况参数(即转速或燃料流量)进行识别。
(4)调取与待分析数据同工况的叶片状态识别模型,将待分析数据所得的转子叶片通过频率幅值矩阵输入该模型进行计算。若叶片状态分析模型计算结果显示叶片状态异常,则进行下一步分析,否则判断为叶片未发生断裂故障。
(5)分析燃气轮机转子工频幅值、工频振动相对相位是否发生突变。若存在突变,则判断为燃气轮机发生叶片断裂故障,否则判断为未发生该故障。
5 燃气轮机叶片故障案例数据分析
某型燃气轮机安装了振动数据实时采集系统,采样频率为51.2kHz,4个振动加速度测点布置在机匣外支承上。燃气轮机在稳定工况运行过程中发生了叶片断裂故障,断裂前后振动速度有效值趋势,如图3所示。
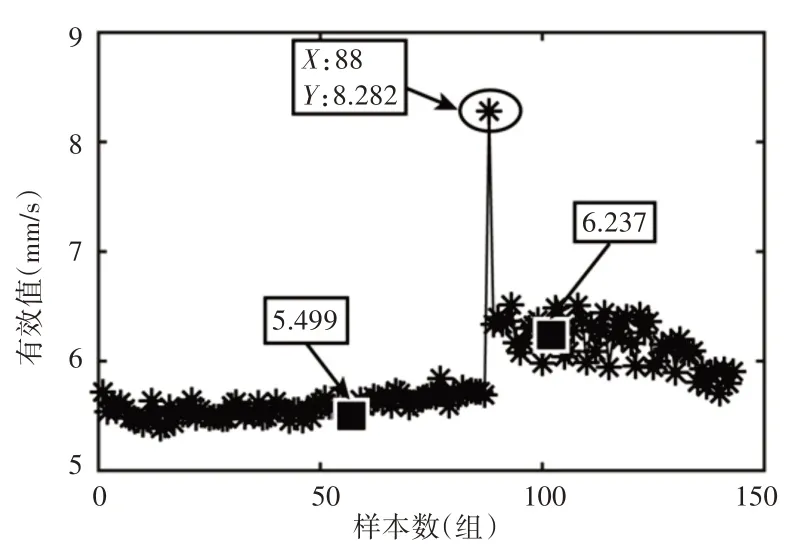
图3 叶片断裂前后振动有效值变化趋势Fig.3 Trend of Effective Value of Vibration Before and After Blade Fracture
由图3可知,机组在第88组样本对应时刻,振动有效值发生明显突变,突变前后振动有效值基本稳定。突变前振动速度有效值稳定于5.5mm∕s左右,突变瞬间振动速度有效值达到近8.3mm∕s,突变后振动速度有效值稳定于6.2mm∕s左右。由于现场振动报警阈值为15mm∕s,因此在振动突变后仍运行了一段时间,直至人听到异响才停车。同时,在数据回放时发现了上述振动速度有效值突变现象,但仅根据有效值分析难以实现故障诊断和定位,因此现场只能通过逐级孔探来确认故障原因,发现第九级叶片出现了断裂故障。利用提出的诊断方法对燃气轮机上述突变前后运行数据进行分析,以期在故障发生瞬间进行识别与告警。
5.1 建立OCSVM叶片状态分析模型
燃气轮机发生故障阶段对应的燃机转速为6900r∕min,输出功率为15MW。利用故障发生一周前相同工况的40组数据作为训练样本,建立叶片状态分析模型。提取训练数据的叶片通过频率幅值组成特征参数矩阵A,利用粒子群算法进行参数寻优,适应度函数为n折交叉验证OCSVM分类准确率的平均值,粒子群算法具体参数设置及寻优结果,如表1所示。
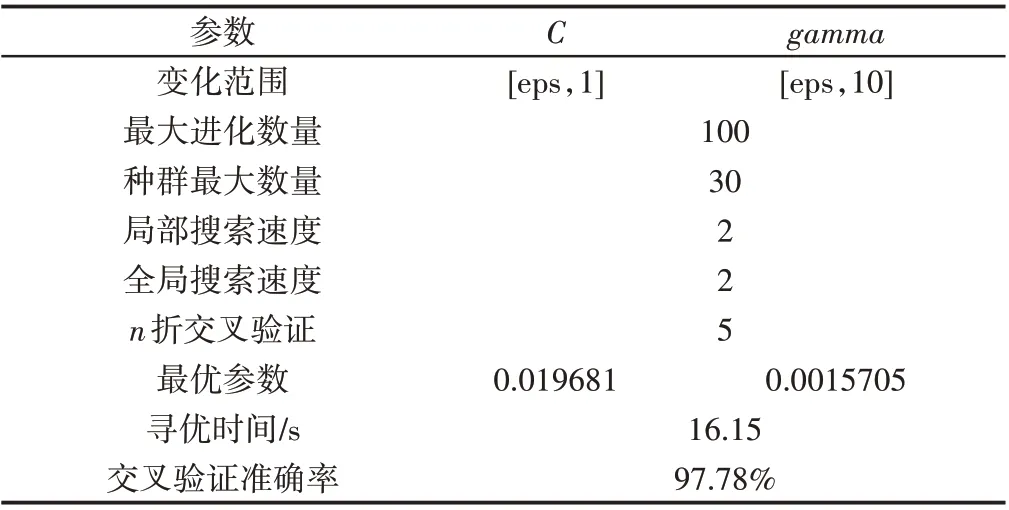
表1 粒子群算法寻优参数设置及结果Tab.1 Particle Swarm Optimization Parameter Setting and Results
由上表可知OCSVM控制参数寻优结果如下:最优惩罚因子Cini= 0.019681,最优gammaini= 0.0015705。基于特征参数矩阵A和最优控制参数,核函数选用高斯核,利用OCSVM建立叶片状态分析模型。对模型输出结果定义如下:输出结果为“−1”,表示叶片为正常状态;输出结果为“+1”,表示叶片出现了断裂故障。
5.2 故障数据分析
将图3对应的故障当天87组振动突变前样本和56组振动突变后样本作为输入,利用第(2)步建立的叶片状态分析模型进行计算。模型输出结果,如图4所示。结果统计,如表2所示。
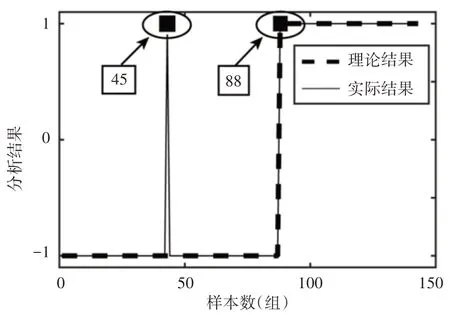
图4 叶片状态分析模型的输出结果Fig.4 Output of Blade State Analysis Model
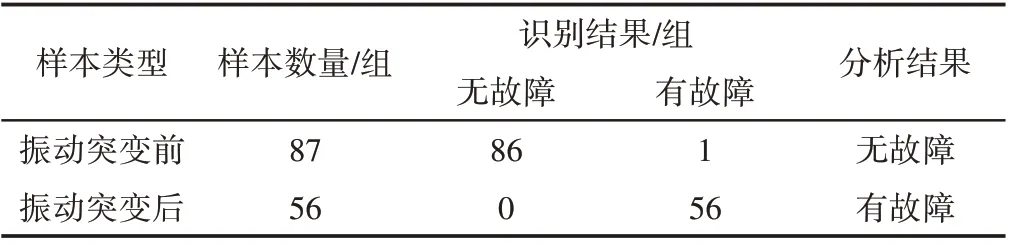
表2 叶片状态分析模型输出结果统计Tab.2 Statistics of Blade State Analysis Model Output
由表2 可知,自第88 组样本开始(即振动速度有效值突变后),叶片状态分析模型即判断为叶片出现了异常。因此进行下一步工频振动的分析。
5.3 转子工频振动分析
振动速度有效值突变前后转子工频幅值的变化趋势,如图5所示。
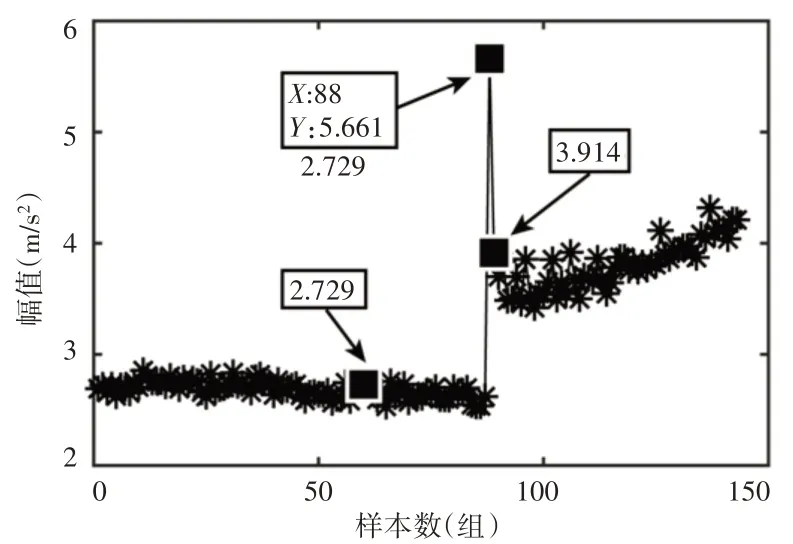
图5 转子工频幅值变化趋势图Fig.5 Rotor Power Frequency Amplitude Change Trend Chart
由图5可知:(0~87)#样本(即振动速度有效值突变时刻)前,转子工频幅值基本稳定于2.7m∕s2左右;88#样本,转子工频幅值达到5.66m∕s2;(89~143)#样本(即振动速度有效值突变后),转子工频幅值从3.9m∕s2逐渐增大。即:转子工频幅值在88#样本前后发生了明显突变。进一步地,对前截面水平、垂直两方向转子工频相对相位差进行分析,其变化趋势,如图6所示。
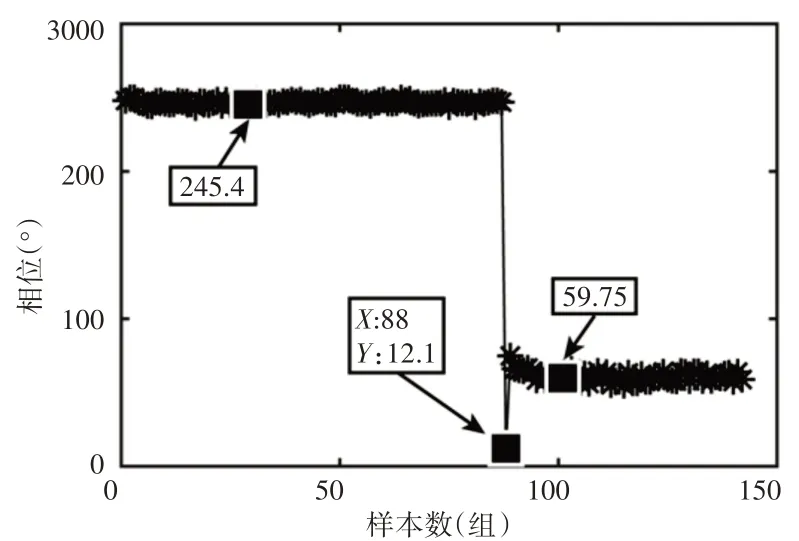
图6 前截面水平−垂直测点转子工频相对相位变化趋势图Fig.6 Rotor Power Frequency Relative Phase Change Trend Graph of Front Section Horizontal−Vertical Measuring Points
由图6可知:(0~87)#样本(即振动速度有效值突变前),转子工频相对相位差稳定于245°左右;88#样本,转子工频相对相位差达到12.1°;(89~143)#样本(即振动速度有效值突变后),转子工频相对相位差稳定于60°左右。即:转子工频振动相对相位在88#样本前后发生了明显突变。
5.4 故障诊断结论
根据叶片通过频率幅值,基于OCSVM的叶片状态分析模型判断为自第88 组样本开始叶片出现了异常;同时,转子工频幅值、转子工频振动相对相位在88#样本前后发生了明显突变。结合上述分析结果,根据提出的方法判断该燃气轮机在88#样本对应时刻发生叶片断裂故障。
该燃机在停车后通过孔探发现其第九级动叶片出现了多处断裂,上述分析结论与故障现象一致,验证方法的有效性。
6 结论
针对燃气轮机转子动叶片断裂故障,结合叶片尾流激振力产生机理和断裂叶片引发的转子突发不平衡故障振动机理,对叶片断裂故障诊断方法进行了研究,得到的主要结论如下:
(1)综合叶片通过频率成分振动幅值、工频成分振动幅值和同截面工频成分振动相对相位可作为燃气轮机叶片断裂故障的敏感特征集,可指导工程中燃气轮机叶片状态监测。
(2)基于OCSVM 的燃气轮机叶片断裂故障识别模型,结合叶片断裂引发的突发不平衡振动特征进行叶片断裂故障诊断,可用于燃气轮机叶片断裂故障的分析诊断。同时,该模型无需大量叶片断裂案例数据进行训练,更便于实际工程应用。在实际案例分析中,上述方法成功实现了叶片断裂故障的诊断。

