基于变分模态分解和压缩感知的电力系统宽频振荡监测方法

陈志同，徐 晋，李国杰，汪可友

基于变分模态分解和压缩感知的电力系统宽频振荡监测方法

陈志同，徐 晋，李国杰，汪可友

(上海交通大学电力传输与功率变换控制教育部重点实验室，上海 200240)

随着“双碳”目标的提出，未来电力系统会有更高比例可再生能源及电力电子设备并网，会引发电力系统新型宽频振荡问题。因此针对电力系统宽频振荡“高噪声”和“宽频带”的特点，提出一种基于变分模态分解和压缩感知的自适应宽频振荡监测方法。对变分模态分解(variational mode decomposition, VMD)方法进行改进，自适应确定模态分解数，抑制噪声分量并监测识别振荡信号的有效信息。若监测到宽频振荡，将降噪处理后的宽频振荡数据通过压缩感知(compressed sensing, CS)方法上传，在调度中心对压缩数据进行重构，精确恢复宽频振荡信号，方便调度主站后续分析处理。算例表明所提方法可在高强度随机噪声的情况下保持宽频振荡监测的质量，克服高速采样后数据传输带宽的限制，并在实际电力系统宽频振荡信号监测中有良好应用。

宽频振荡；变分模态分解；压缩感知；监测方法

0 引言

随着碳达峰、碳中和目标的提出，我国能源将加快向绿色清洁转型，未来电力系统会有高比例可再生能源及与此相关的高比例电力电子设备(“双高”)并网[1]。高渗透率的“双高”设备相互作用将明显改变电力系统的动态特性和运行方式，导致电力系统频发新型宽频振荡失稳现象，典型的如鲁西柔性直流输电与弱交流电网相互作用引发的1270 Hz高频振荡[2-3]。与传统的电力系统振荡不同，宽频振荡频率分布在几赫兹至几千赫兹且噪声干扰严重，会严重威胁电力系统的安全稳定运行，而现有监测方法主要针对工频信号，无法为宽频发生机理和运行控制研究提供数据支撑[4-7]。因此，有必要针对宽频振荡现象开展新的监测方法研究，为仿真机理分析及系统的预防保护控制提供数据参考。

宽频振荡监测主要面临“高噪声”和“宽频带”两大新的挑战。一方面，由于新能源发电、储能及电动汽车的大规模接入，且电力电子开关动作频繁，致使宽频信号受高强度噪声污染严重。电力系统常用的信号监测方法有Prony算法[8-9]、小波变换法[10-12]、经验模态分解(empirical mode decomposition, EMD)[13-16]、变分模态分解(variational mode decomposition, VMD)[17-19]等。Prony算法可用指数函数的线性组合来估计各振荡频率的成分，但对噪声比较敏感且无法处理非平稳信号[8-9]。小波变换法能够对噪声起到抑制作用，但降噪的精度过分依赖小波基的选取[10-12]。EMD将信号分解为个本征模态函数(intrinsic mode function, IMF)，利用希尔伯特变换(hilbert transform, HT)实现对振荡信息的测量，但EMD存在端点效应、模态混叠等问题，无法分离频率相近的分量，会导致宽频信号测量不准确[13-16]。VMD算法弥补了EMD的不足，但宽频振荡可能存在多个振荡频率，分解数值难以选择，且部分噪声会掺杂在有效IMF中无法消除[17-19]。如何快速抑制高强度随机噪声并有效识别振荡信息是宽频监测研究的关键问题。

另一方面，宽频振荡的频率监测范围远高于传统振荡。为了满足电力系统电力电子化的发展要求，IEEE标准协会将宽频信号的频率范围扩展至0～ 9 kHz。然而目前电力系统中广泛运用的信号监测装置是同步向量测量装置(phasor measurement units, PMU)，PMU设计之初仅能够测量45～55 Hz工频基波向量，2017年国家电网对PMU功能进行改造后能够支持10～40 Hz和60～90 Hz范围内的次超同步振荡监测，但是依然无法涵盖整个宽频频段[20-21]。许多研究者针对如何扩大PMU的频率监测范围进行了研究，但都不能克服PMU装置自身采样速率低的局限，无法有效应对宽频监测需求[22-25]。通过高速采样能够覆盖整个宽频频带，如电子式互感器和电磁式互感器，均能满足采样范围(9 kHz内)的要求，在此基础上可以设计宽频振荡监测方法。但高频高精度采样将得到海量数据，受现有带宽的限制无法实现监测数据高速通信，而铺设光纤或5G通信费用极高，难以满足泛在需求，推广应用受到限制[26-30]。如何在高速采样下实现宽频带数据传输是宽频监测研究的另一个关键问题。

针对现有方法在宽频振荡监测上存在的问题，本文提出一种基于变分模态分解和压缩感知的电力系统宽频振荡监测新方法。本文将按照以下内容进行展开，第1节对所提宽频振荡监测方法进行整体设计；第2节针对宽频振荡多模态和高噪声的难题对VMD算法进行改进，设计了自适应模态分解法，并通过自相关系数与阈值相结合的方法抑制噪声分量并保留振荡信号的有效信息，完成宽频振荡识别监测；第3节在监测到宽频振荡的情况下，基于压缩感知方法将有效振荡数据压缩上传，克服高速采样所需传输的宽频振荡数据量大的问题，并在调度中心通过稀疏度自适应匹配追踪算法对压缩数据进行重构，精确恢复压缩信号，方便调度主站后续分析处理；第4节通过算例验证本文所提方法对于“高噪声”和“宽频带”的宽频振荡信号的监测效果，并在实际电力系统宽频振荡信号监测中检验。

1 宽频振荡监测方法整体设计

为有效克服高强度随机噪声的干扰和高速采样后数据量传输剧增的问题，实现宽频振荡的有效监测，本文针对性地提出一种宽频振荡监测方法，其整体设计框图如图1所示。

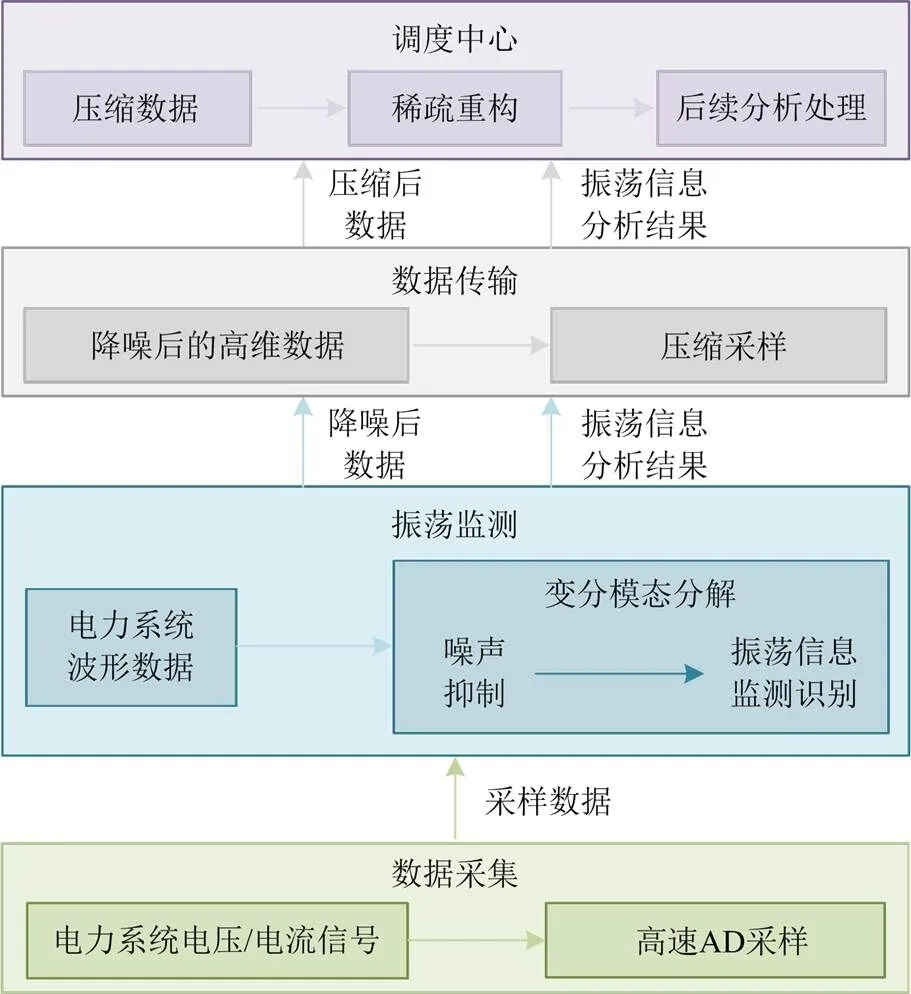
图1 宽频振荡监测方法整体设计框图

主要步骤包括：

1) 数据采集。对电力系统电压/电流信号进行高频采样及模数转换，采用25.6 kHz(512点/周期)的采样频率，将能够测量的宽频信号范围覆盖至0～9 kHz。

2) 振荡监测。通过优化改进VMD算法实现宽频振荡的准确监测。针对宽频带内可能存在的多个分量，自适应调整模态分解数并将信号分解为个IMF。由于信号可能夹杂着高强度随机噪声，通过自相关系数计算去除纯噪声IMF，并对剩余含噪IMF做进一步的阈值降噪处理，降噪处理后的含噪IMF为有效IMF，然后通过HT变换实现各有效IMF频率、幅值的测量，完成振荡监测。

3) 数据传输。如果监测到基频以外的振荡信息，由于面临高速采样数据量剧增的难题，采用压缩感知(compressed sensing, CS)方法对高维宽频降噪信号进行压缩采样，突破Nyquist采样定理的瓶颈，将压缩后的数据传输至调度中心[31-33]。

4) 调度中心。获得压缩的监测数据后，采用稀疏度自适应匹配追踪算法(sparsity adaptive matchingpursuit, SAMP)，通过迭代逼近方法完成信号重构。研究人员可以根据需要对振荡数据进行后续分析处理。

2 基于VMD的宽频振荡监测

2.1 VMD原理

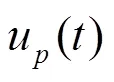
1) 变分问题构造

假设输入信号可以分解为个IMF分量u()，通过希尔伯特变换解析，得到其单边频谱为

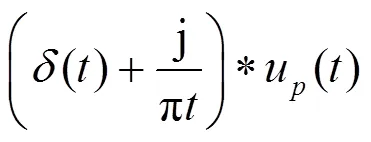
预估各IMF解析信号中心频率，将每个模态u()的频谱转移到相应基带得到

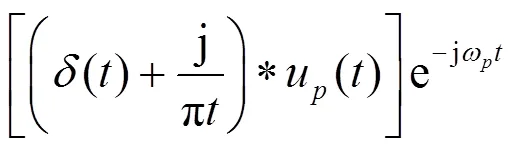
式中，ω为各预估的中心频率。

根据以上解调信号的高斯光滑度和梯度平方L2范数准则，估计各模态带宽，可以将受约束的VMD变分模型表示为

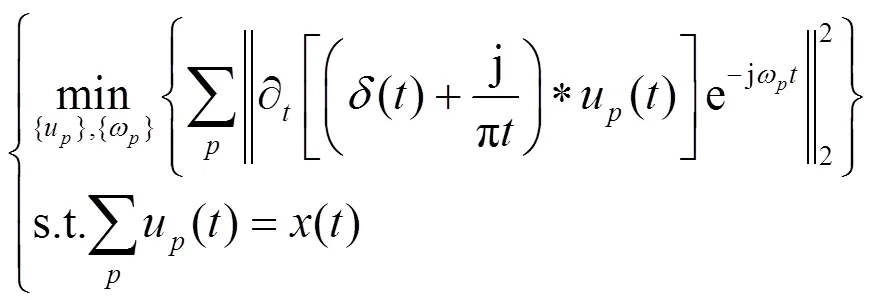
2) 变分问题求解

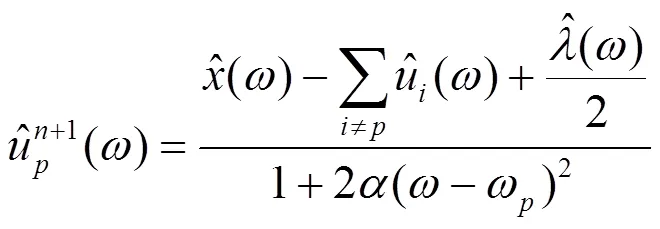
中心频率ω的迭代方法为

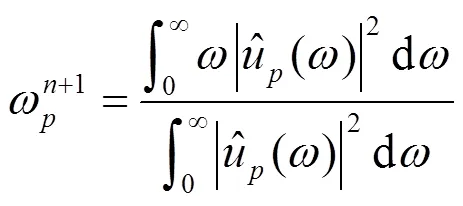
从最终算法看，VMD非常简单高效，VMD将信号分解为非递归、变分模态分解模式，各模态直接在频域更新迭代，最后转换到时域。

2.2 自适应模态分解

由于宽频带频率分量可能有一个或多个，数量无法预知，VMD算法存在模态数值难以选择的问题。当值较大时，会导致过分解，模态中含有虚假分量，当值较小时，分解不够彻底。因此，需要对算法进一步优化，自适应确定分解层数。

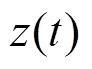
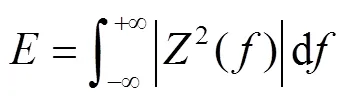
当的取值不合适时，某一频率可能分解到不止一个模态分量中。假设宽频振荡信号()在频率下的幅值为，若分解到两个模态中，幅值分别为1和2，1和2不为0，则必有

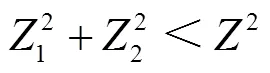
因此，的取值不合适时分解后的信号能量会减少。原信号和VMD分解的各模态分量频谱的能量计算公式为

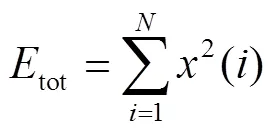
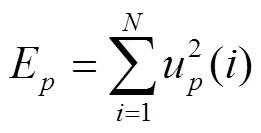
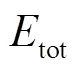
定义能损量来衡量VMD分解效果，能损量表达式为

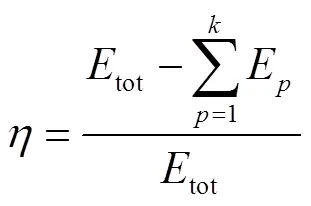
在逐次增加的情况下，当VMD分解达到最优时，最小且接近于0，此时值即为自适应最优模态数。

2.3 噪声抑制与振荡识别

“双高”电力系统信号受严重的高强度随机噪声影响，可将随机噪声表达为

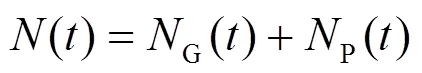
VMD分解后，部分随机噪声会分离到纯噪声IMF中，另一部分会掺杂在有效IMF中。本文通过计算各分量的自相关系数，对纯噪声IMF和含噪IMF做出区分，自相关系数的计算公式为

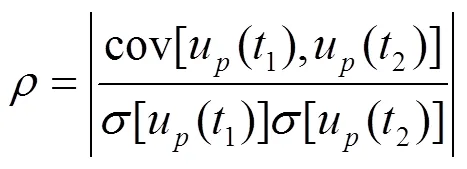
去除纯噪声IMF后，对每个掺杂噪声的含噪IMF进一步降噪。在频谱内按自适应阈值进行检测，如果所在频率幅值超过阈值，则予以保留，如果低于阈值则强制置零，即

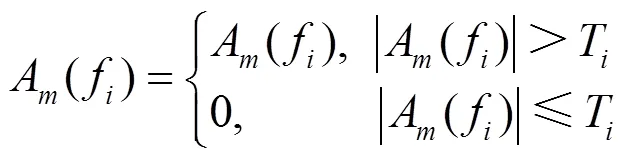
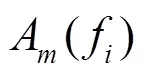
通过上述降噪过程可以得到最大程度保持宽频振荡信息的有效IMF。分析有效IMF的中心频率并通过HT变换得到有效IMF对应的幅值，如果监测到宽频振荡，则上传振荡分析结果和降噪后的数据，整个振荡监测的流程图如图2所示。

图2 振荡监测流程图

3 基于压缩感知的宽频数据传输

3.1 CS原理

若监测到宽频振荡，将宽频振荡信息和降噪后的有效振荡数据经传输网络上传至调度中心。由于现有带宽的限制难以实现宽频振荡信号的传输，采用新的高速通信成本剧增，因此希望在保持信号可恢复的情况下对数据进行压缩传输。本文采用CS方法解决上述难题。只要信号通过稀疏变换基变换到某一域后稀疏，就可以用一个不相关的测量矩阵对宽频振荡信号降维，大大减少宽频振荡的数据传输量，上传后通过求解优化问题即可重构出原宽频信号，供调度中心后续分析。

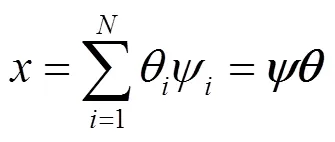
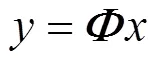
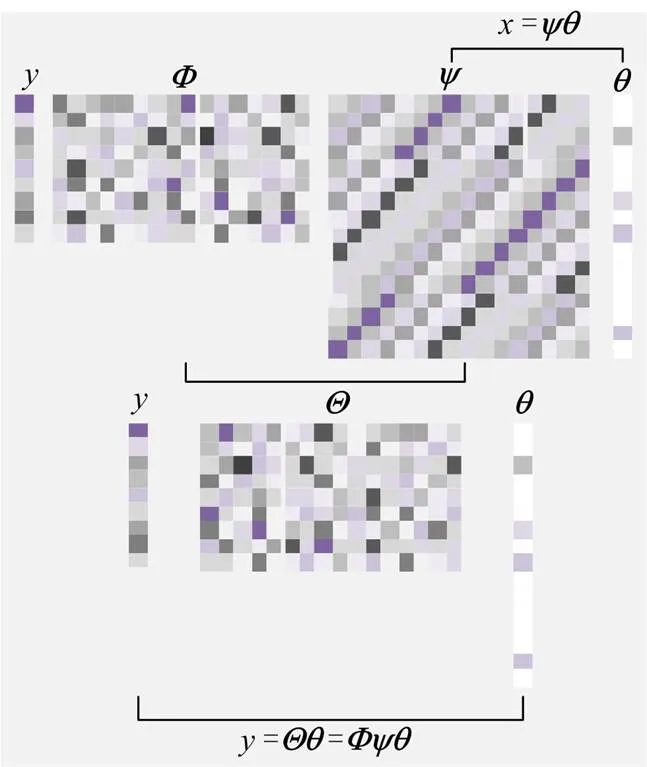
图3 压缩感知的矩阵表示

将式(14)代入式(15)中，可以得到

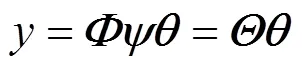
宽频振荡数据压缩传输及调动中心重构的过程如图4所示。

图4 压缩感知框图

3.2 感知矩阵确定

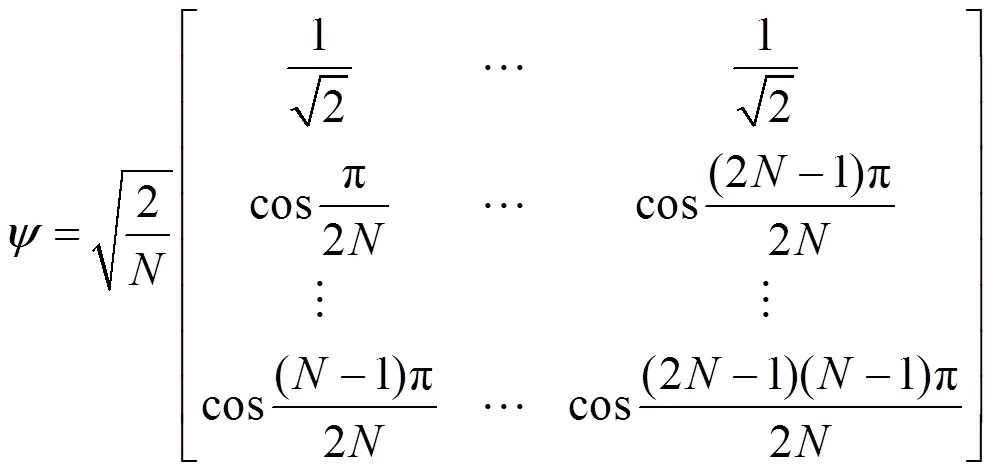
3.3 稀疏度自适应重构算法

鉴于实际应用中，宽频振荡信号可能有多个振荡模态，稀疏度无法预知，本文采用SAMP算法重构信号。SAMP算法无需将信号的稀疏度作为先验知识，可以通过步长自适应迭代逼近原信号。SAMP算法具体步骤如下。

2) 初始化：残差初始值0，候选集0，支撑集0，步长初始值0，迭代次数初始值1，步长倍数初始值1。

4) 将当前列索引支撑集J与先前候选集F-1合并，得到新的候选集F。

6) 更新残差

SAMP算法流程如图5所示。

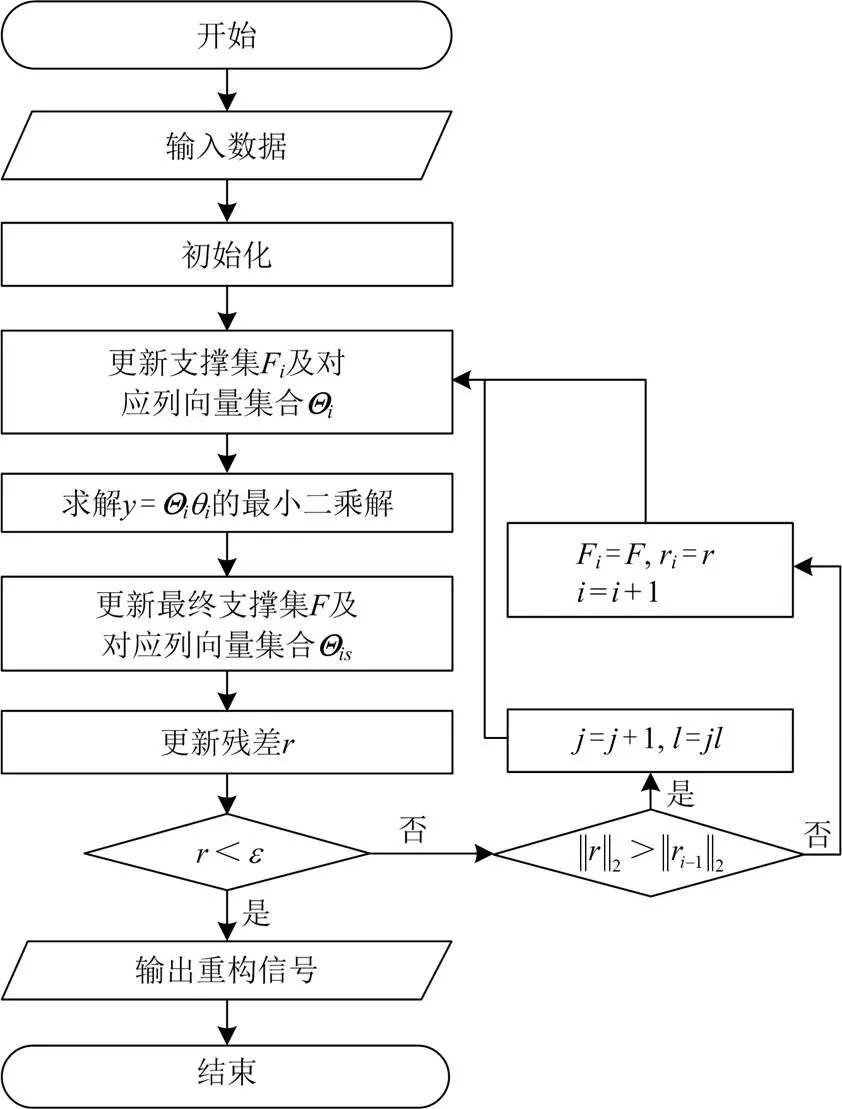
图5 SAMP算法流程图

4 算例分析

4.1 高噪声多模态振荡监测测试

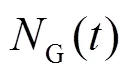
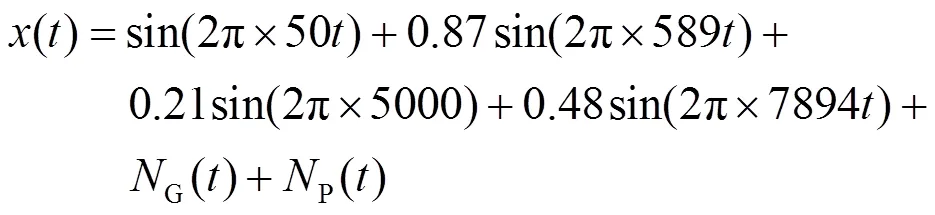
对于所设计方法对多模态宽频振荡现象的监测精度，将频率相对误差(frequency relative error, FRE)和幅值相对误差(amplitude relative error, ARE)作为判断指标，即

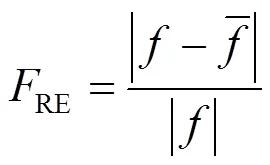
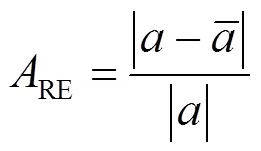
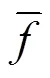
对于所设计方法在高强度随机噪声干扰下的有效性，本文将相对均方根误差(relative root mean square error, RRMSE)和信噪比(signal to noise ratio, SNR)作为评价指标，即

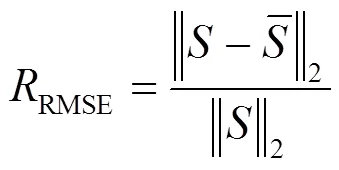
1) 多模态监测测试

表1 不同p取值下的能损量(无噪)

VMD分解结果如图6所示，左半部分为IMF部分时域分解结果，通过HT计算各IMF振荡信息，幅频结果如右半部分所示，通过测试结果可以看出本文方法可以有效将各IMF分离，且能有效识别各IMF振荡信息。

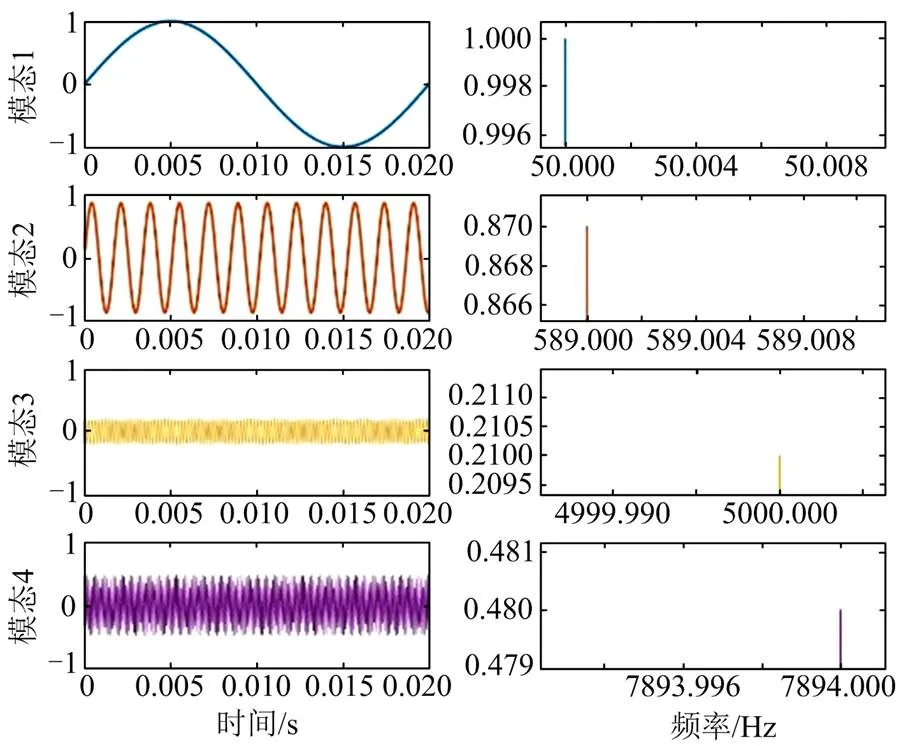
图6 多模态监测结果

2) 加入高强度随机噪声测试

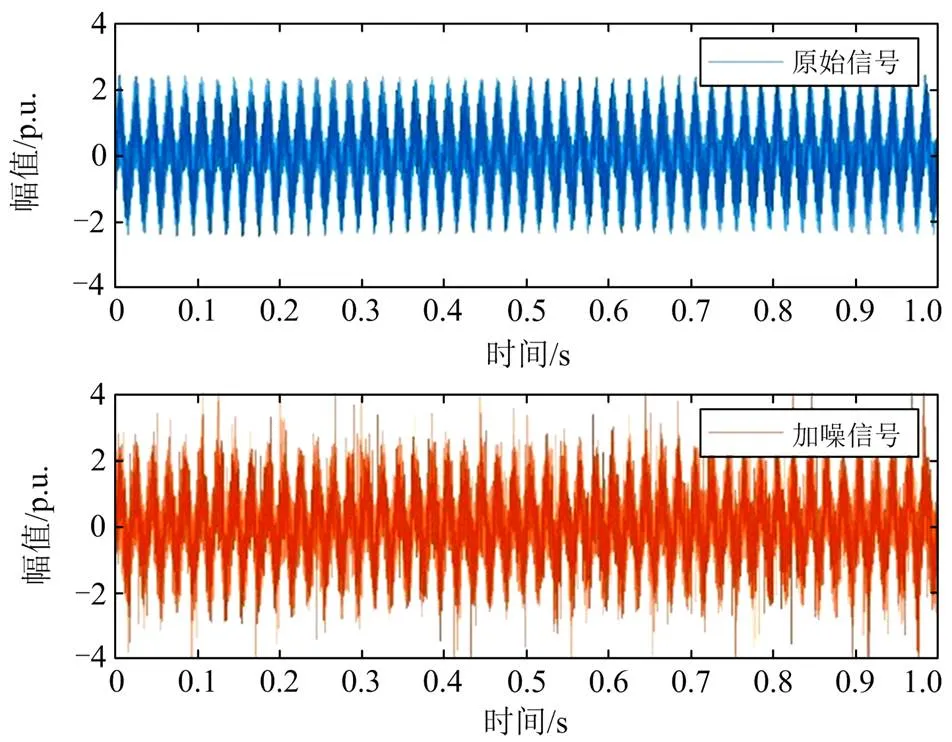
图7 宽频原始信号和加噪信号仿真

通过计算，加入噪声后信号相对均方根误差为0.4233，可见噪声对原始信号干扰严重。对加噪信号进行自适应模态分解，结果如表2所示，在=5时最小且接近于0，确定最优模态数为5。

表2 不同p取值下的能损量(加噪)

各模态中心频率由低频到高频分布，分解结果如图8所示。计算各IMF的自相关系数，分别为0.9922、0.9785、0.6571、0.9066和0.0056，可以判断前4个分量为含噪IMF，最后一个分量为纯噪声IMF，所提方法能够区分出含噪IMF和纯噪声IMF。

图8 VMD分解的各IMF波形

舍弃纯噪声IMF并将此过程命名为一次降噪，保留其余4个含噪IMF，此时相对均方根误差为0.2009，噪声含量降低52.54%。虽然降噪效果明显，但噪声含量依然较多。继续对各含噪IMF进行阈值降噪，进一步去除含噪IMF中的噪声分量，将此过程命名为二次降噪。用RRMSE和SNR对两次降噪效果进行定量评价，前后对比结果如表3所示。

表3 降噪效果对比

从表3中可以看出，经过两次降噪处理后，RRMSE小于1%，SNR也大大提高，加入其中的噪声基本完全去除。为更直观地观察降噪后信号与未加噪声的原信号的关系，绘制两者的时域波形如图9所示，由整体波形知降噪信号与原信号吻合度高，随机选取局部图像进行放大，可以看出局部波形高度重合，降噪信号在消除噪声的同时能够保留原信号的有效振荡信息。

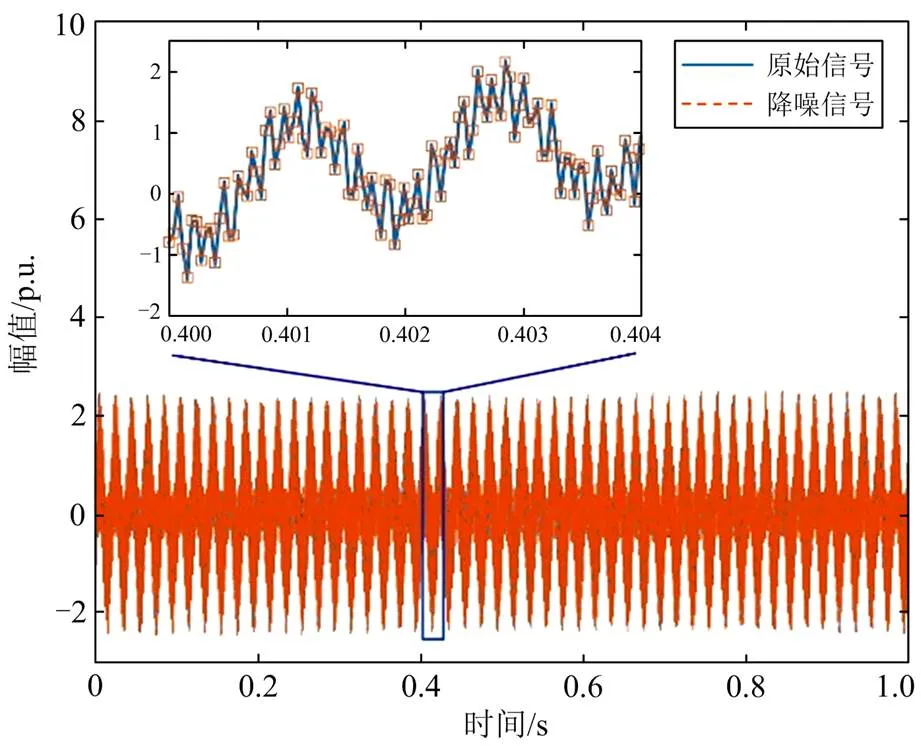
图9 宽频降噪信号与原始信号对比

在降噪完成后对有效IMF进行分析，通过HT变换得到各IMF的频率、幅值，验证所提方法对于振荡信息的监测精度，振荡信息分析结果如表4所示。监测结果显示FRE和ARE都很小，在抑制噪声干扰后可以准确识别振荡信息。由于宽频信号有频域稀疏的特点，而VMD算法直接在频域迭代，求解迅速，后续拟通过现场可编程逻辑门阵列(FPGA)和高性能数字信号处理器(DSP)芯片实现本文宽频振荡监测的现场应用。同时宽频振荡不是全网型的振荡，集中发生在光伏发电、风电发电的并网接入点和柔直换流站等位置，只需要在这些位置部署宽频振荡监测，通过升级更高性能的硬件即可满足采样和计算的效率要求，具有可行性。

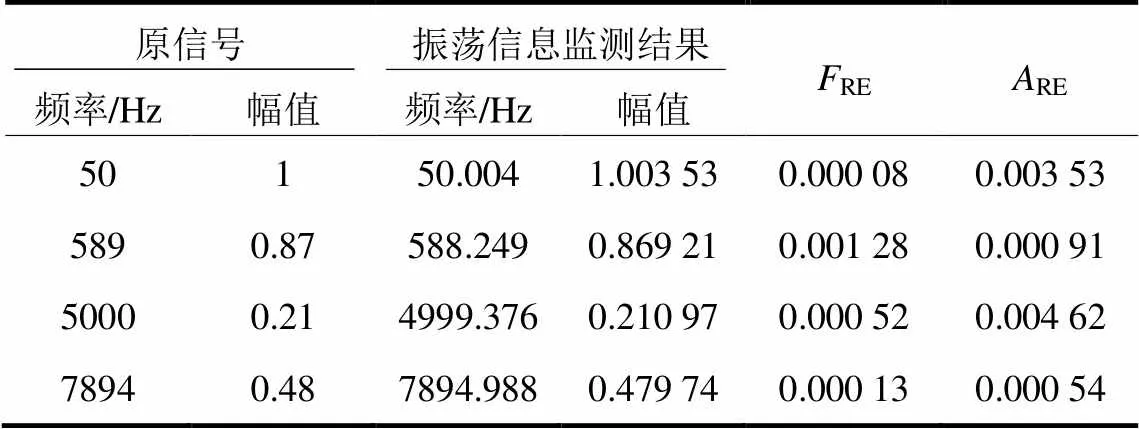
表4 宽频振荡监测结果

3) 与其他方法对比测试

为进一步验证本文所提方法的效果，对测试信号分别采用小波硬阈值[10]、小波软阈值[12]、EMD方法[15]进行分析对比，结果如表5所示。可以看出本文方法的信噪比较大，相对均方根误差较小。因此相对于以上方法，本文通过改进VMD方法，自适应确定最优分解模态数，并通过自相关系数与阈值相结合的方法完成噪声抑制和有效信号的监测，更适合在高噪声多模态的宽频振荡信号中应用。

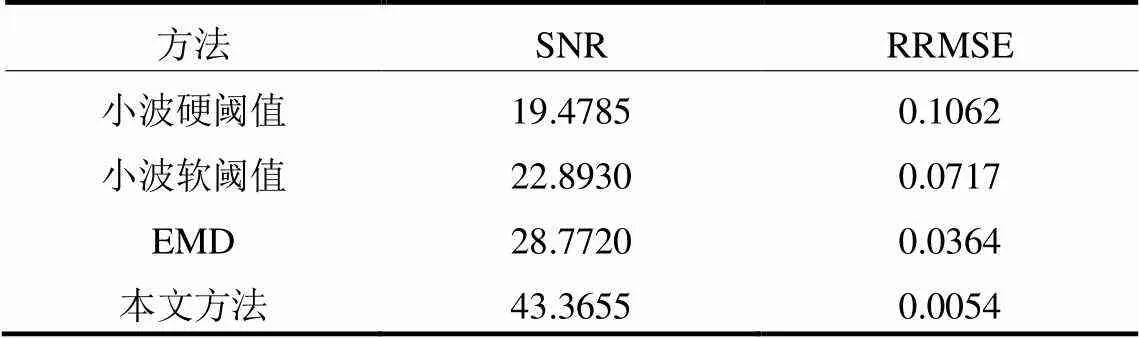
表5 不同监测方法效果对比

4.2 数据压缩传输测试

在监测到宽频振荡后，验证本文所设计的基于压缩感知的宽频数据传输方法将数据压缩上传到调度中心的能力。由于高频采样产生海量高维数据，采用压缩感知方法对数据进行压缩传输时，设置数据压缩比(compression ratio, CR)为

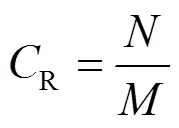
为了验证所提压缩感知方法在数据高压缩比下的重构精度，CR取0.1。降噪后的待传输信号数据与压缩采样后的数据散点图如图10所示，时域分布明显稀疏。

由于对压缩信号重构的前提是信号在某一变换域内稀疏，验证原信号在离散余弦变换基上的系数分布，如图11所示，可以看出信号经过稀疏矩阵变换后明显稀疏，仅存在为数不多的非零值，符合压缩感知的应用场景。

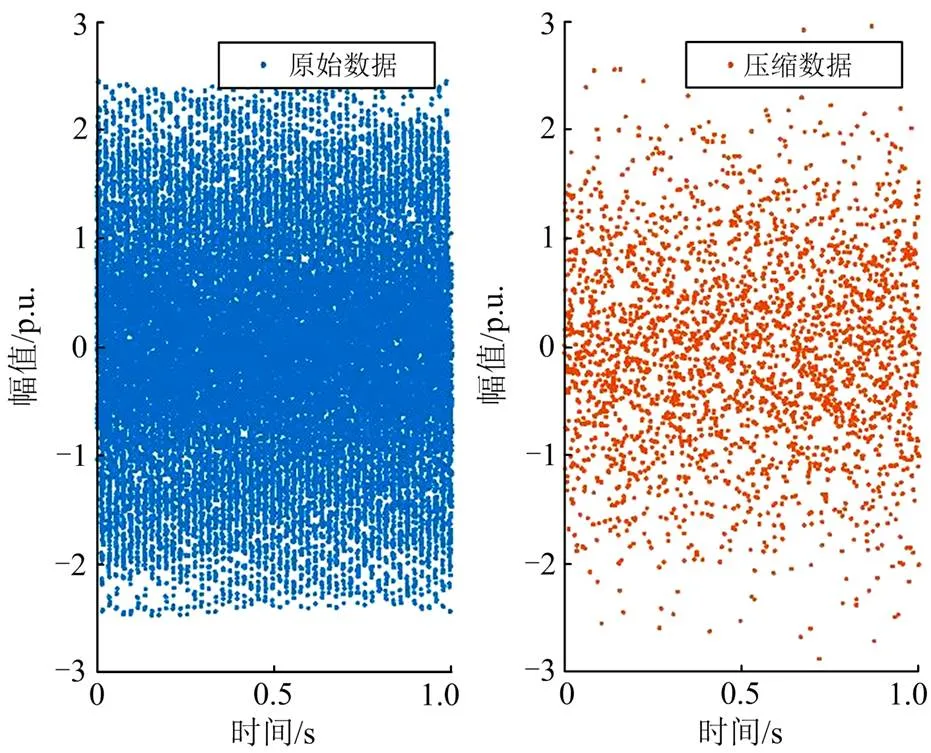
图10 待传输宽频振荡信号原始数据与压缩数据

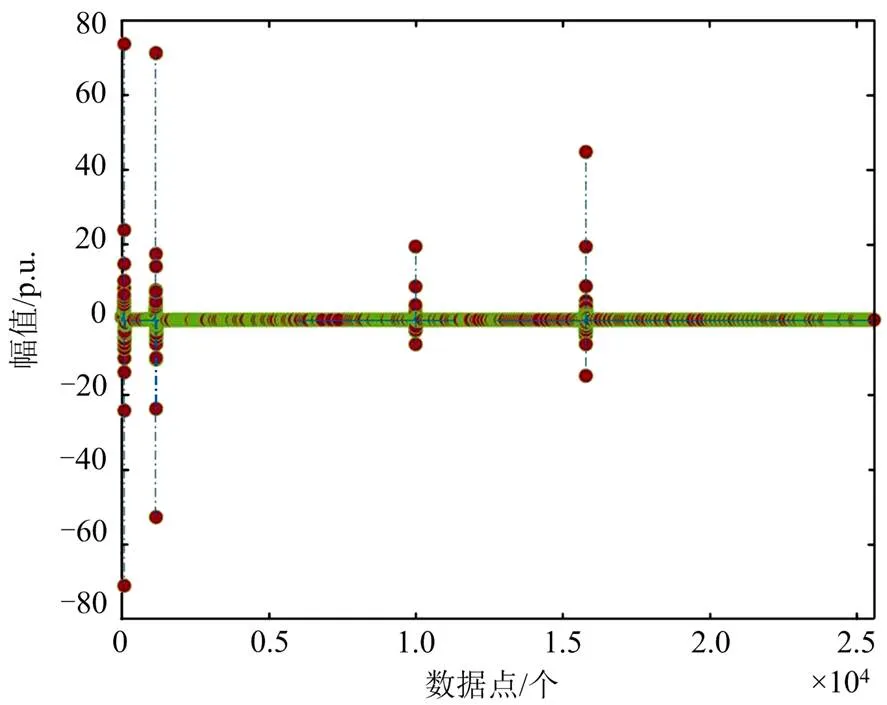
图11 宽频振荡信号稀疏矩阵变换波形

在信号经过测量矩阵压缩采样后，对压缩感知方法降低信号数据传输量的性能进行量化分析。在仿真时间为1 s的情况下，以25.6 kHz进行采样得到25 600个数据，每个采样数据的数据类型为double型，则在Nyquist采样定理框架下每秒需要传输200 KB数据。若采用压缩比为0.1的采样方式，每秒内需要传输的数据仅为Nyquist采样定理框架下的1/10，只需传输20 KB数据。随着采样频率的提升和采样时间的增加，通过压缩感知方法将更大程度地减少数据传输。

在数据上传到调度中心后，通过SAMP算法处理压缩数据，对原始数据进行重构，重构的时域频域波形及重构误差如图12所示，经计算，重构后的RRMSE为0.0066，误差非常小。因此，通过压缩感知方法可以实现数据压缩传输，并在调度中心重构原始数据，供相关人员后续分析。

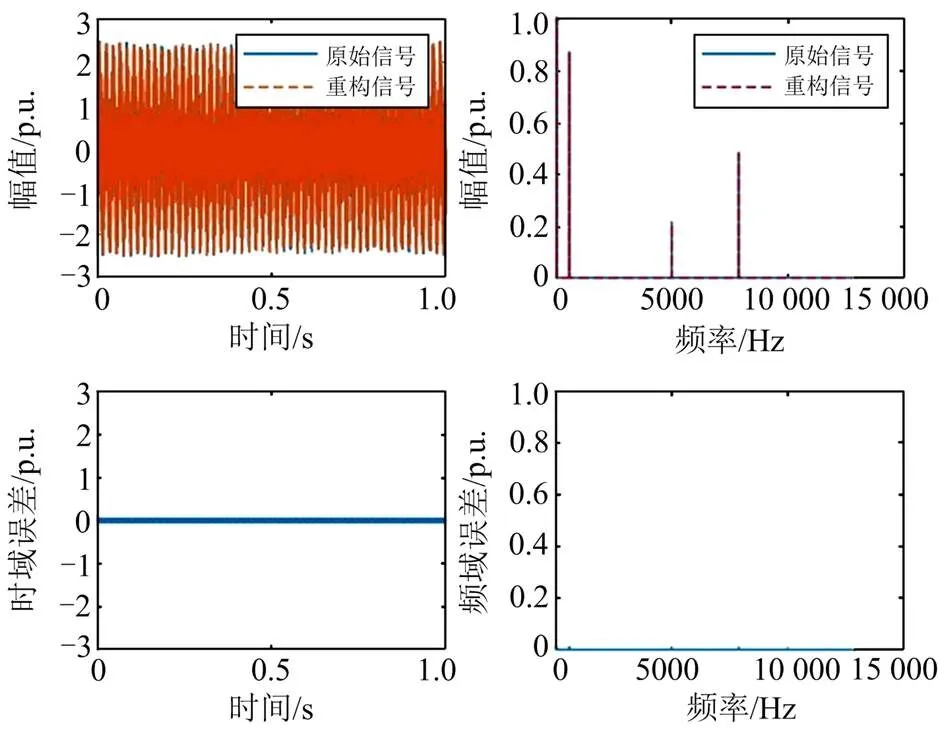
图12 压缩感知重构时频波形及误差对比

4.3 宽频振荡现场数据测试

为了验证本文方法在宽频振荡实际监测中的效果，对华北某风电场的实测数据进行测试，该风电场直流端对端结构示意图如图13所示。

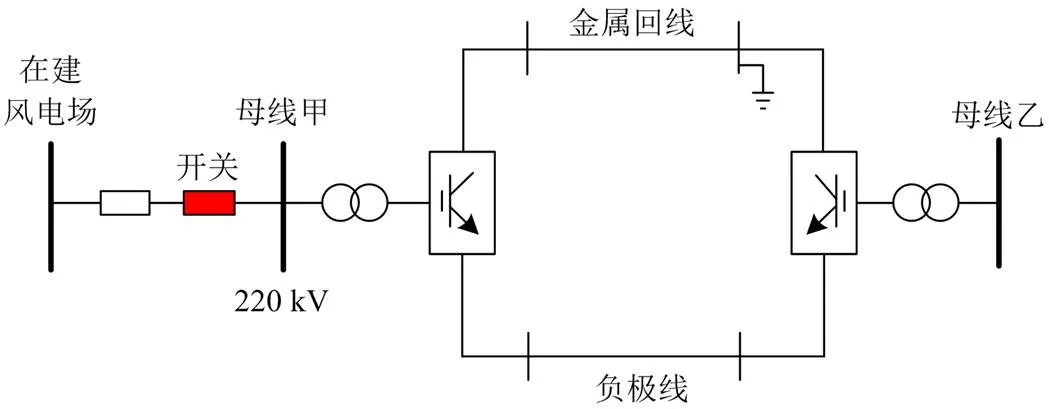
图13 华北某风电场直流端对端结构示意图

在风电场接入启停调试期间，母线甲和母线乙端对端负极单极运行，正极为检修状态。母线甲为孤岛运行模式，直流功率为零。合入红色开关前后母线甲侧的部分电压录波数据如图14所示，可以明显看出母线甲电压出现宽频振荡现象。

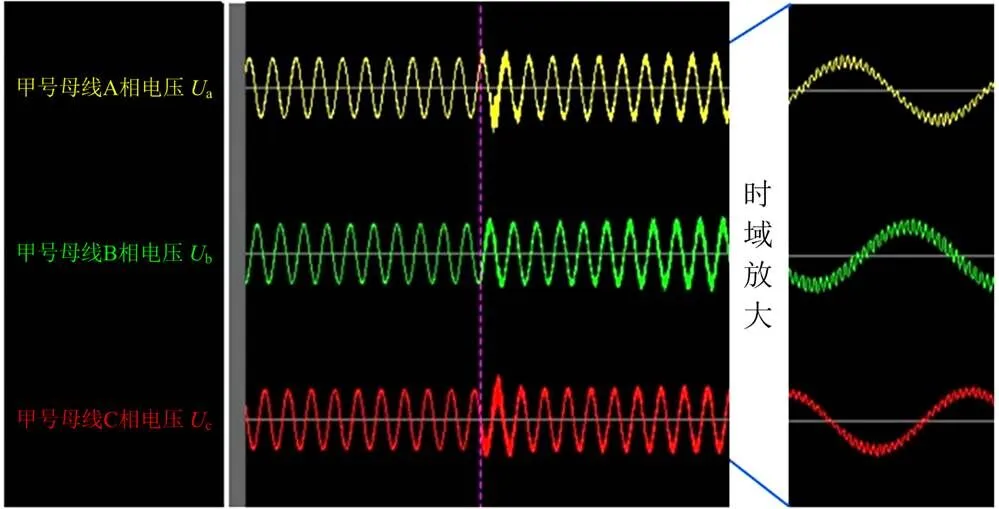
图14 母线甲电压录波

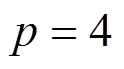
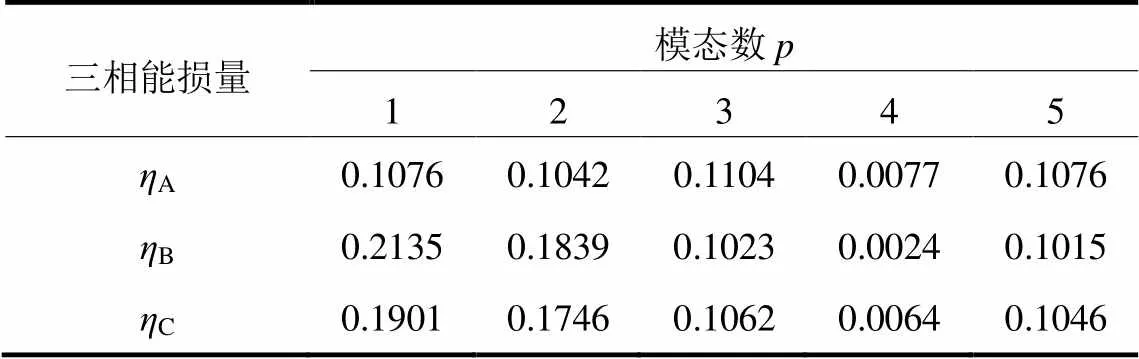
表6 母线甲三相电压不同p取值下的能损量

以A相电压为例，VMD的分解结果如图15所示。计算各IMF的自相关系数，分别为0.9915、0.5830、0.5328和0.1516，可以判断前3个分量为含噪IMF，最后一个分量为纯噪声IMF，B相和C相同理。

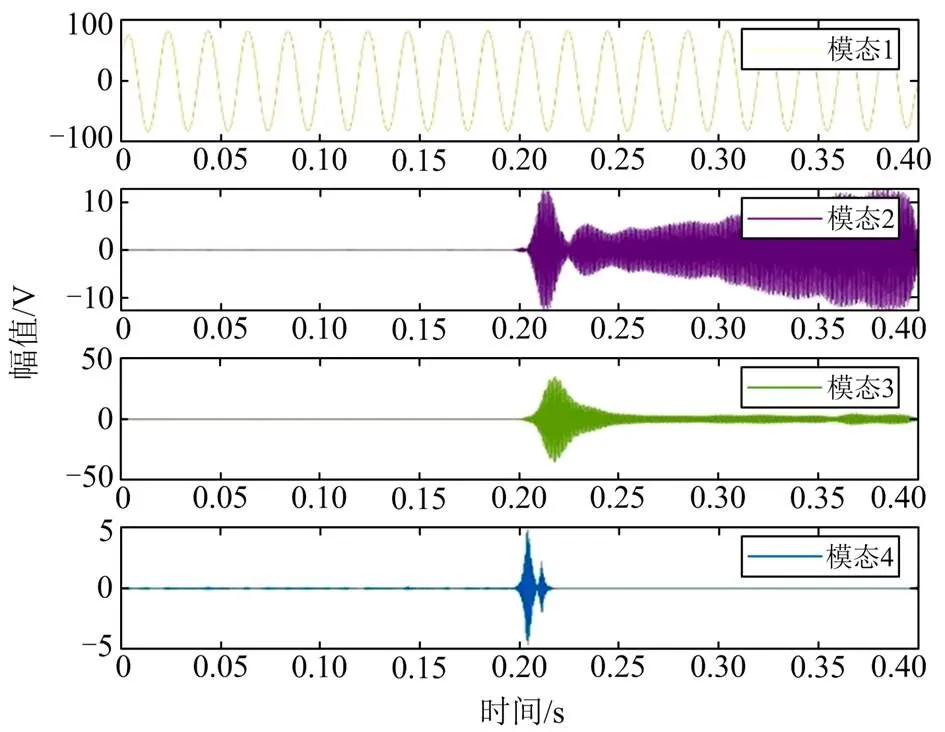
图15 A相电压的VMD分解波形

舍弃纯噪声IMF，并对各含噪IMF进行阈值降噪，完成后分析有效振荡信息。母线甲三相电压的监测结果如表7所示。可以看出风电场测试合入红色开关后确实发生宽频振荡，除基频50 Hz外出现2个频率分量，宽频振荡频率集中在1507.5 Hz和 1607.5 Hz。监测到宽频振荡后，闭锁换流阀，切除振荡线路，用时0.441 s，能够满足实时性要求。根据初步分析认为是风电场投入220 kV交流线路后，换流阀与交流线路构成LC振荡，从而产生宽频振荡分量。

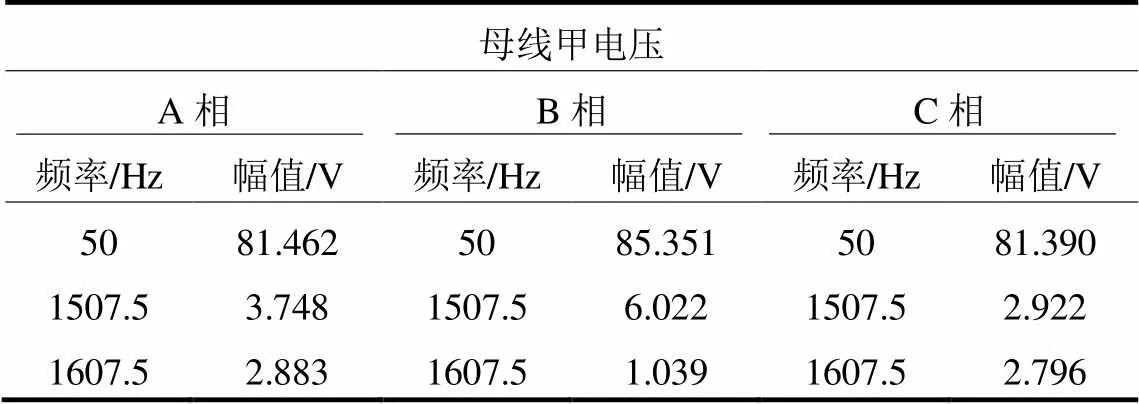
表7 母线甲电压宽频监测结果

将初步振荡分析结果与降噪后的宽频采集数据通过压缩感知上传至调度中心并在调度中心进行重构，压缩比取0.1。以A相为例，待传输的宽频振荡数据与压缩采样后的数据散点图如图16所示。

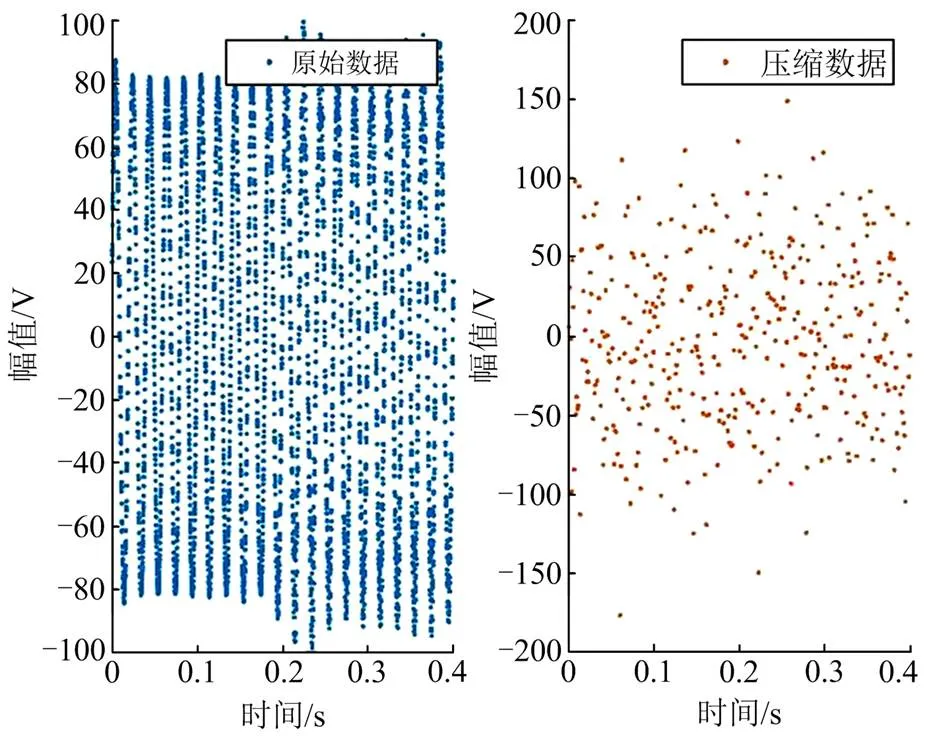
图16 A相宽频数据与压缩数据

可以看出经过压缩后数据明显稀疏。将压缩数据上传，并在调度中心对宽频振荡数据进行重构。母线甲电压的重构信号如图17所示。研究人员可以在宽频振荡数据的基础上对事故进行后续分析处理。

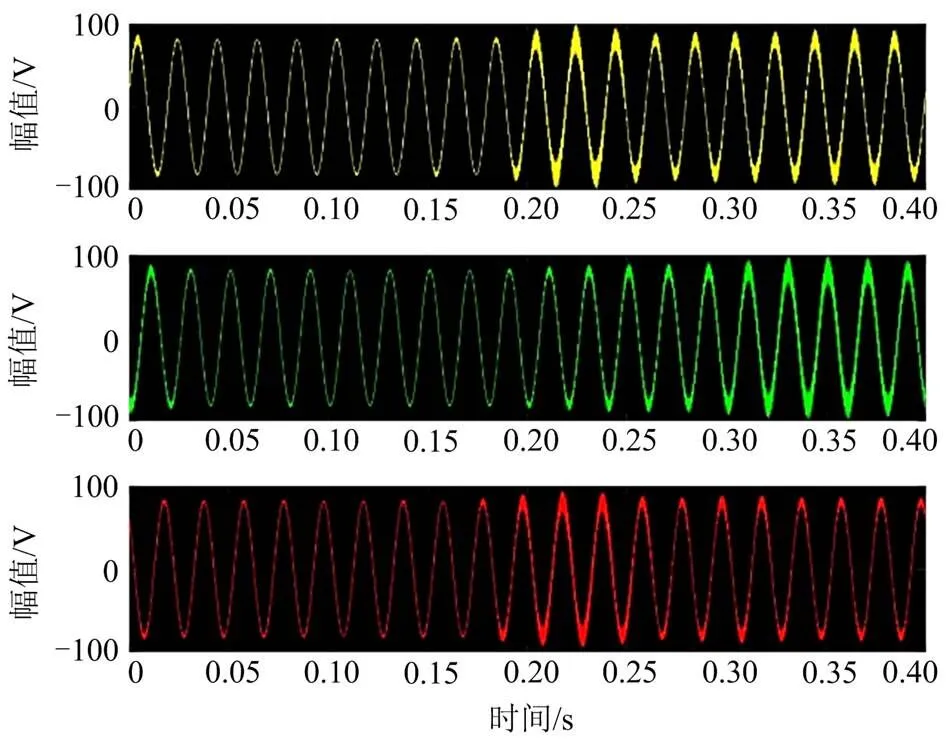
图17 母线甲电压重构波形

5 结论

针对宽频振荡“高噪声”和“宽频带”的难题，本文提出一种基于变分模态分解和压缩感知的电力系统宽频振荡监测的新方法，主要结论如下：

1) 对变分模态分解进行优化使它能够自适应确定最优模态分解数，并通过自相关系数与阈值相结合的方法，实现噪声的抑制并监测振荡的有效信息。算例证明所提方法更适用于高噪声多模态的宽频振荡信号。

2) 使用高斯随机矩阵作为测量矩阵，压缩上传振荡数据。结合宽频振荡信号频域稀疏的特点选择DCT基作为稀疏矩阵，通过SAMP算法在调度中心对压缩数据进行精确重构。算例证明所提方法能够突破Nyquist采样定理的限制，大大减少数据传输量。

3) 本文所提方法可应用于风电等电力电子设备引起的宽频振荡现象的监测和分析，监测电网动态行为变化，为调度人员提供分析数据。

[1] 李晖, 刘栋, 姚丹阳. 面向碳达峰碳中和目标的我国电力系统发展研判[J]. 中国电机工程学报, 2021, 41(18): 6245-6259.

LI Hui, LIU Dong, YAO Danyang. Analysis and reflection on the development of power system towards the goal of carbon emission peak and carbon neutrality[J]. Proceedings of the CSEE,2021, 41(18): 6245-6259.

[2] 张天翼, 王海风. 风电并入弱交流系统引发次同步振荡的研究方法综述[J]. 电力系统保护与控制, 2021, 49(16): 177-187.

ZHANG Tianyi, WANG Haifeng. Research methods for subsynchronous oscillation induced by wind power under weak AC system: a review[J]. Power System Protection and Control, 2021, 49(16): 177-187.

[3] 姜齐荣, 王玉芝. 电力电子设备高占比电力系统电磁振荡分析与抑制综述[J]. 中国电机工程学报, 2020, 40(22): 7185-7201.

JIANG Qirong, WANG Yuzhi. Overview of the analysis and mitigation methods of electromagnetic oscillations in power systems with high proportion of power electronic equipment[J]. Proceedings of the CSEE, 2020, 40(22): 7185-7201.

[4] 赵妍, 孙硕, 柳旭, 等. 基于改进CNN-LSTM的电力系统宽频振荡辨识[J]. 智慧电力, 2022, 50(2): 48-54.

ZHAO Yan, SUN Shuo, LIU Xu, et al. Identification of power system wide-band oscillation based on improved CNN-LSTM[J]. Smart Power, 2022, 50(2): 48-54.

[5] 谢小荣, 刘华坤, 贺静波, 等. 电力系统新型振荡问题浅析[J]. 中国电机工程学报, 2018, 38(10): 2821-2828, 3133.

XIE Xiaorong, LIU Huakun, HE Jingbo, et al. On new oscillation issues of power systems[J]. Proceedings of the CSEE, 2018, 38(10): 2821-2828, 3133.

[6] 孙名扬, 王艳, 张琦兵, 等. 电网宽频广域监测主站构建关键技术研究及应用[J]. 电网与清洁能源, 2021, 37(8): 84-91.

SUN Mingyang, WANG Yan, ZHANG Qibing, et al. Study and application of key technologies constructing power grid wide-frequency and wide-area monitoring system[J]. Power System and Clean Energy, 2021, 37(8): 84-91.

[7] 李亦伦. 一起风电场高频振荡事故的原因和解决方法分析[J]. 电力系统保护与控制, 2021, 49(9): 135-142.

LI Yilun. Analysis on causes and solutions of a high frequency oscillation accident in wind farm[J]. Power System Protection and Control, 2021, 49(9): 135-142.

[8] 张俊峰, 杨婷, 陈珉, 等. 基于Prony滑动平均窗算法的电力系统低频振荡特征分析[J]. 电力自动化设备, 2018, 38(10): 178-183.

ZHANG Junfeng, YANG Ting, CHEN Min, et al. Power system low-frequency oscillation characteristic analysis based on Prony moving average window algorithm[J]. Electric Power Automation Equipment, 2018, 38(10): 178-183.

[9] 郭成, 尹轲, 张艳萍, 等. 一种基于综合DFT和Prony算法的谐波与间谐波分析方法[J]. 电力系统保护与控制, 2021, 49(17): 1-9.

GUO Cheng, YIN Ke, ZHANG Yanping, et al. A harmonic and interharmonic analysis method based on integrated DFT and Prony algorithm[J]. Power System Protection and Control, 2021, 49(17): 1-9.

[10] OSKOOI B, JULAYUSEFI M, GOUDARZI A. GPR noise reduction based on wavelet thresholdings[J]. Arabian Journal of Geosciences, 2015, 8(5): 2937-2951.

[11] 李国庆, 王丹, 姜涛, 等. 基于递归连续小波变换的电力系统振荡模式辨识[J]. 电力自动化设备, 2016, 36(9): 8-16.

LI Guoqing, WANG Dan, JIANG Tao, et al. Power system oscillation mode identification based on recursive continuous wavelet transform[J]. Electric Power Automation Equipment, 2016, 36(9): 8-16.

[12] 姜涛, 刘方正, 陈厚合, 等. 基于多通道快速傅里叶小波变换的电力系统主导振荡模式及模态协同辨识方法研究[J]. 电力自动化设备, 2019, 39(7): 125-132.

JIANG Tao, LIU Fangzheng, CHEN Houhe, et al. Cooperated identification method of dominant oscillation modes and mode shapes for power system based on multi-channel fast Fourier transform based continuous wavelet transform[J]. Electric Power Automation Equipment, 2019, 39(7): 125-132.

[13] 许峰, 李开成, 王可. 基于EMD和卡尔曼滤波的振荡信号检测[J]. 电测与仪表, 2015, 52(24): 60-64.

XU Feng, LI Kaicheng, WANG Ke. The detection of oscillation signal based on EMD and Kalman filter[J] Electrical Measurement & Instrumentation, 2015, 52(24): 60-64.

[14] YANG Gongliu, LIU Yuanyuan, WANG Yanyong, et al. EMD interval thresholding denoising based on similarity measure to select relevant modes[J]. Signal Processing, 2015, 109: 95-109.

[15] 王雨虹, 董瑞. 改进EMD的多信号Prony电力系统低频振荡分析[J]. 控制工程, 2019, 26(7): 1335-1340.

WANG Yuhong, DONG Rui. Improved low frequency oscillation analysis based on multi-signal power system[J]. Control Engineering of China, 2019, 26(7): 1335-1340.

[16] 沈钟婷, 丁仁杰. 基于改进EMD去噪和矩阵束的电力系统低频振荡模态辨识[J]. 应用科学学报, 2019, 37(6): 761-774.

SHEN Zhongting, DING Renjie. Power system low frequency oscillation mode identification based on improved EMD denoising and matrix pencil algorithm[J]. Journal of Applied Sciences, 2019, 37(6): 761-774.

[17] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[18] 闫红艳, KWON H J, 高艳丰. 基于类噪声数据的电力系统低频振荡模态参数辨识[J]. 发电技术, 2022, 43(1): 19-31.

YAN Hongyan, KWON H J, GAO Yanfeng. Modal parameter identification of low frequency oscillation in power system based on ambient data[J]. Power Generation Technology, 2022, 43(1): 19-31.

[19] 汤吉鸿, 朱军飞, 李勇, 等. 基于变分模态分解的电力系统泛频带振荡辨识方法[J]. 电力系统保护与控制, 2019, 47(2): 1-8.

TANG Jihong, ZHU Junfei, LI Yong, et al. VMD based mode identification for broad-band oscillation in power system[J]. Power System Protection and Control, 2019, 47(2): 1-8.

[20] 薛禹胜, 徐伟, 万秋兰. 关于广域测量系统及广域控制保护系统的评述[J]. 电力系统自动化, 2007, 31(15): 1-5, 16.

XUE Yusheng, XU Wei, WAN Qiulan. A review of wide area measurement system and wide area control system[J]. Automation of Electric Power Systems, 2007, 31(15): 1-5, 16.

[21] 谢小荣, 王银, 刘华坤, 等. 电力系统次同步和超同步谐波相量的检测方法[J]. 电力系统自动化, 2016, 40(21): 189-194.

XIE Xiaorong, WANG Yin, LIU Huakun, et al. Detection method for sub-synchronous and super-synchronous harmonic phasors in power system[J]. Automation of Electric Power Systems, 2016, 40(21): 189-194.

[22] 黄星宇, 罗萍萍, 龚锦霞, 等. 新能源并网系统次同步谐波相量检测方法[J]. 电力系统保护与控制, 2020, 48(13): 38-44.

HUANG Xingyu, LUO Pingping, GONG Jinxia, et al. Subsynchronous harmonic phasor detection in a renewable energy grid-connected system[J]. Power System Protection and Control, 2020, 48(13): 38-44.

[23] MOHD Z, MOHD R, MOHD T S. A novel method for locating the source of sustained oscillation in power system using synchrophasors data[J]. Protection and Control of Modern Power Systems, 2020, 5(4): 51-62.

[24] 刘灏, 李珏, 毕天姝, 等. 一种自适应同步相量测量方法[J]. 中国电机工程学报, 2018, 38(17): 5063-5071, 5303.

LIU Hao, LI Jue, BI Tianshu, et al. An adaptive synchrophasor measurement method[J]. Proceedings of the CSEE, 2018, 38(17): 5063-5071, 5303.

[25] 刘革明, 白杨, 任祖怡, 等. 次同步振荡监测控制系统的研究与实现[J]. 电力系统保护与控制, 2018, 46(2): 131-136.

LIU Geming, BAI Yang, REN Zuyi, et al. Research and implementation on monitoring and controlling system of sub synchronous oscillation[J]. Power System Protection and Control, 2018, 46(2): 131-136.

[26] 樊陈, 姚建国, 常乃超, 等. 面向电力电子化电网的宽频测量技术探讨[J]. 电力系统自动化, 2019, 43(16): 1-8, 57.

FAN Chen, YAO Jianguo, CHANG Naichao, et al. Discussion on wide-frequency measurement technology for power electronized power grid[J]. Automation of Electric Power Systems, 2019, 43(16): 1-8, 57.

[27] 吴艳平, 姚建国, 常乃超, 等. 多功能宽频测量装置的设计与实现[J]. 电力系统自动化, 2020, 44(20): 136-141.

WU Yanping, YAO Jianguo, CHANG Naichao, et al. Design and implementation of multi-functional wide-frequency measurement device[J]. Automation of Electric Power Systems, 2020, 44(20): 136-141.

[28] 樊陈, 姚建国, 常乃超, 等. 电网宽频振荡实时监测技术方案[J]. 电力系统自动化, 2021, 45(11): 152-159.

FAN Chen, YAO Jianguo, CHANG Naichao, et al. Technical scheme for real-time monitoring of wide- frequency oscillation in power grid[J]. Automation of Electric Power Systems, 2021, 45(11): 152-159.

[29]ZHANG Hengxu, JIN Zongshuai, TERZIJA V. An adaptive decomposition scheme for wideband signals of power systems based on the modified robust regression smoothing and Chebyshev-II IIR filter bank[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 220-230.

[30] 黄冬冬, 李江涛, 何双, 等. 用于特高压换流变压器宽频特性测量的脉冲发生器设计[J]. 高压电器, 2022, 58(7): 191-198.

HUANG Dongdong, LI Jiangtao, HE Shuang, et al. Design of pulse generator for measurement of broadband characteristics of UHV converter transformer[J]. High Voltage Apparatus, 2022, 58(7): 191-198.

[31] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[32] 杨挺, 武金成, 袁博. 谐波和间谐波检测的压缩感知恢复算法[J]. 中国电机工程学报, 2015, 35(21): 5475-5482.

YANG Ting, WU Jincheng, YUAN Bo. The restoration algorithm of compressed sensing to detect harmonic and inter-harmonic[J]. Proceedings of the CSEE, 2015, 35(21): 5475-5482.

[33] 刘嫣, 汤伟, 刘宝泉. 基于压缩感知的电能质量扰动数据稀疏分析与改进重构算法[J]. 电工技术学报, 2018, 33(15): 3461-3470.

LIU Yan, TANG Wei, LIU Baoquan. Data sparse analysis and improved reconstruction algorithm of power quality disturbance based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3461-3470.

Monitoring method of power system wide-band oscillation based on variational mode decomposition and compressive sensing

CHEN Zhitong, XU Jin, LI Guojie, WANG Keyou

(Key Laboratory of Control of Power Transmission and Conversion, Shanghai Jiao Tong University, Shanghai 200240, China)

With the proposal of the "double carbon" goal, a higher proportion of renewable energy and power electronic equipment will be connected to the grid in the future. This will cause the problem of wide-band oscillation. Therefore, according to the characteristics of "strong noise" and "wide band", a monitoring method of power system wide-band oscillation based on variational mode decomposition and compressive sensing is proposed. The variational mode decomposition (VMD) method is improved to adaptively determine the number of mode decompositions, reduce noise and monitor the effective information of the oscillation signal. If the wide-band oscillation is detected, the wide-band oscillation data after noise reduction is uploaded by a compressed sensing (CS) method. The compressed data is reconstructed in the dispatching center to accurately recover the wide-band oscillation signal. This is convenient for the subsequent analysis of the dispatching station. Numerical examples show that the proposed method can maintain the quality of wide-band oscillation monitoring when there is high-intensity random noise, overcome the limitation of data transmission bandwidth after high-speed sampling, and has a good application to wide-band oscillation signal monitoring of an actual power system.

wide-band oscillation; variational mode decomposition; compressive sensing; monitoring method

10.19783/j.cnki.pspc.220252

国家自然科学基金青年项目资助(52107113)；国家自然科学基金面上项目资助(51877133)；国家电网有限公司华东分部项目“针对沿海及海上大规模风电接入的电网全电磁暂态仿真和宽频振荡评估技术”

This work is supported by the Youth Fund of National Natural Science Foundation of China (No. 52107113).

2022-03-02；

2022-07-31

陈志同(1998—)，男，硕士研究生，研究方向为电力系统宽频振荡；E-mail: chenzt@sjtu.edu.cn

徐晋(1991—)，男，博士，助理教授，研究方向为电力系统分析、新能源接入、实时仿真与建模等；E-mail: xujin20506@sjtu.edu.cn

李国杰(1965—)，男，博士，教授，博士生导师，研究方向为新能源控制与接入、微电网分析与控制。E-mail: liguojie@sjtu.edu.cn

(编辑 周金梅)